6.2.4+平面向量的数量积(1) 课件(共21张PPT)
文档属性
| 名称 | 6.2.4+平面向量的数量积(1) 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 880.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-08 21:31:45 | ||
图片预览






文档简介
(共21张PPT)
6.2.4 平面向量的数量积(1)
第六章 平面向量及其应用
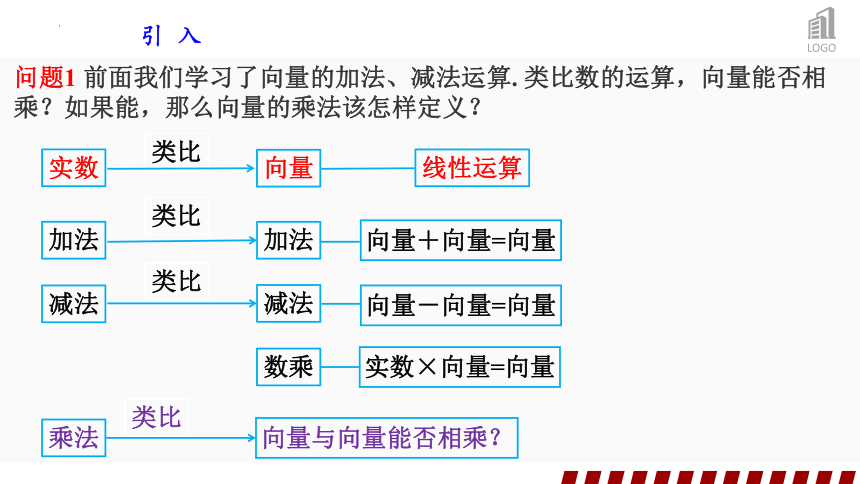
引 入
实数
加法
减法
向量
加法
减法
数乘
向量+向量=向量
向量-向量=向量
实数×向量=向量
向量与向量能否相乘?
乘法
线性运算
类比
类比
类比
类比
问题1 前面我们学习了向量的加法、减法运算. 类比数的运算,向量能否相乘?如果能,那么向量的乘法该怎样定义?
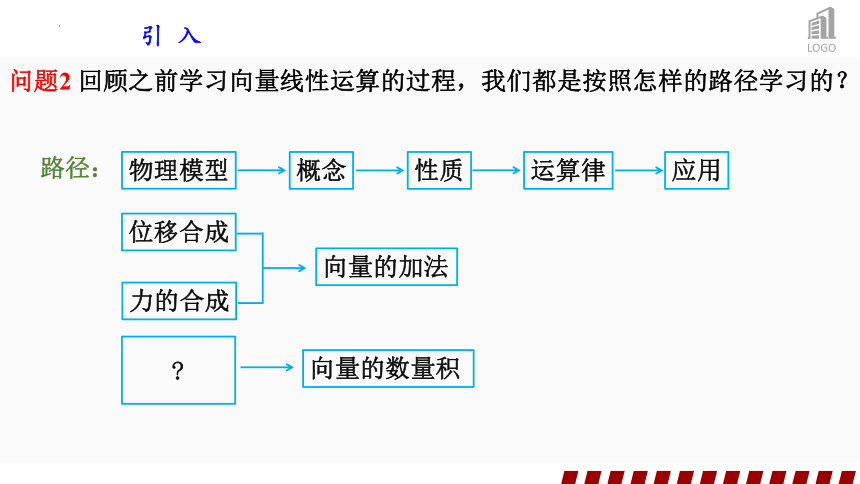
引 入
问题2 回顾之前学习向量线性运算的过程,我们都是按照怎样的路径学习的?
物理模型
性质
运算律
应用
路径:
概念
向量的加法
位移合成
力的合成
向量的数量积
引 入
问题3 ①在物理课中我们学过功的概念:如果一个物体在力F的作用下产生位移s,那么力F所做的功 ,其中θ是F与s的夹角.
功是一个_____,它由力和位移两个向量来确定.
问题3 ②功是一个矢量还是标量?它的大小由哪些量确定?
这给我们一种启示,能否把“功”看成是两个向量“相乘”的结果呢?受此启发,我们引入向量“数量积”的概念.
标量
探究新知
问题4 如果我们将公式中的力与位移类比推广到两个一般向量,其结果又该如何表述?
两个向量的大小及其夹角余弦的乘积
功是力与位移的大小及其夹角余弦的乘积
因为力做功的计算公式中涉及力与位移的夹角,所以我们先要定义向量的夹角概念.
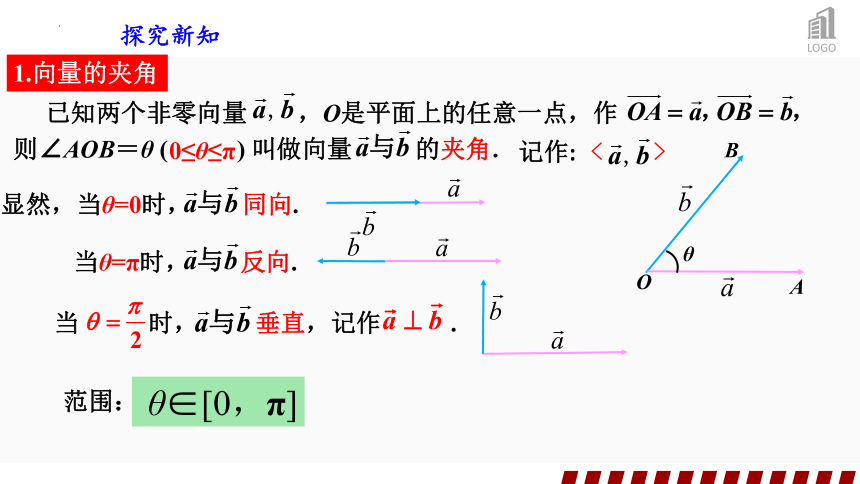
探究新知
1.向量的夹角
已知两个非零向量 ,O是平面上的任意一点,作
则∠AOB=θ ( ) 叫做向量 的夹角.
O
A
B
θ
显然,当θ=0时, 同向.
当 时, 垂直,记作 .
当θ=π时, 反向.
记作:
< >
θ∈[0,π]
范围:
0≤θ≤π
课堂练习
50°
A
B
C
45°
85°
1.在△ABC中,已知A=45°,B=50°,C=85°,求下列向量的夹角:
(1)
45°
130°
85°
45°
130°
85°
(2)
(3)
问题5 两个向量的夹角与两条直线的夹角有何区别?
向量 与 之间的夹角θ的取值范围是[0, π],
注意: 必须共起点.
两直线夹角的范围 是不一样的(向量有方向).
可以平移实现.
探究新知
2.平面向量数量积的定义
已知非零向量 与 ,它们的夹角为θ,我们把数量 叫作
与 的数量积(或内积),记作 ,即规定
规定:零向量与任意向量的数量积为0,即
向量的数量积是一个数量
②一种新的运算.
①“·”不能省略不写,也不能写成“×”.
③数量积a·b的结果为实数,不是向量.(数量积运算是非线性运算)
注意:
例题讲解
例1 已知
解:
例2
解:
由 ,得
∵ ∴ .
知三求一
课堂练习
B
C
C
>
4.已知|a|=6,|b|=8,a与b平行,求a b .
探究新知
问题6 向量的数量积是一个数量,那么它什么时候为正,什么时候为负?
0°≤θ<90°
=90°
④两个非零向量的数量积,符号由夹角θ决定:
注意:
当 a·b=0时,夹角θ_______.
当 a·b>0时,夹角θ范围是_______________;
当 a·b<0时,夹角θ范围是_______________;
90°<θ ≤180°
是非零向量
⑤
探究新知
3.投影向量
设 是两个非零向量, ,过 的起点A和终点B,分别作 所在直线的垂线,垂足分别为A1,B1,得到 ,我们称这种变换为向量 向向量 投影, 叫做向量 在向量 上的投影向量.
我们可以在平面内任取一点O,作 .过点M作直线ON 的垂线,垂足为 ,则 就是向量 在向量 上的投影向量
探究新知
问题7 如图,设与 方向相同的单位向量为 , 与 的夹角为θ,那么 与 , ,θ之间有怎样的关系?
显然 与 共线,于是
所以
当θ为直角时,λ=0,所以
当θ为锐角时,与 方向相同,
探究新知
所以
当θ为钝角时,与 方向相反,
当θ=0时,λ= ,所以
当θ= 时,λ= ,所以
综上可知,对任意的 都有:
例题讲解
例题讲解
例5
课堂练习
【练习】
1.已知a,b满足|a|=2,|b|=1,且a与b的夹角为30°,那么a·b等于____.
2.已知向量a,b满足|a|=1,|b|=4,且a·b=2,则a与b的夹角θ为 .
3.已知e为单位向量,|a|=4,a与e夹角为120°,则a在e方向上的投影向量为 .
探究新知
4.数量积的性质
(3) 当 与 同向时, ;当 与 反向时, .
特别地, 或 .
(由|cosθ|≤1得到)
设a,b是非零向量,它们的夹角是θ,e是与b方向相同的单位向量,则
a a常记为a
可用于求向量的模.
(5)cosθ= .
实质是平面向量数量积的逆用,可用于求两向量的夹角,也称为夹角公式.
课堂小结
1.知识点:
(1)向量的夹角.
(2)向量数量积的定义.
(3)投影向量.
(4)向量数量积的性质.
2.方法归纳:数形结合.
3.易错点:向量夹角共起点;
a·b>0 两向量夹角为锐角,a·b<0 两向量夹角为钝角.
课堂小结
向量数量积
向量
布置作业
(1)教材
(2)同步作业
6.2.4 平面向量的数量积(1)
第六章 平面向量及其应用
引 入
实数
加法
减法
向量
加法
减法
数乘
向量+向量=向量
向量-向量=向量
实数×向量=向量
向量与向量能否相乘?
乘法
线性运算
类比
类比
类比
类比
问题1 前面我们学习了向量的加法、减法运算. 类比数的运算,向量能否相乘?如果能,那么向量的乘法该怎样定义?
引 入
问题2 回顾之前学习向量线性运算的过程,我们都是按照怎样的路径学习的?
物理模型
性质
运算律
应用
路径:
概念
向量的加法
位移合成
力的合成
向量的数量积
引 入
问题3 ①在物理课中我们学过功的概念:如果一个物体在力F的作用下产生位移s,那么力F所做的功 ,其中θ是F与s的夹角.
功是一个_____,它由力和位移两个向量来确定.
问题3 ②功是一个矢量还是标量?它的大小由哪些量确定?
这给我们一种启示,能否把“功”看成是两个向量“相乘”的结果呢?受此启发,我们引入向量“数量积”的概念.
标量
探究新知
问题4 如果我们将公式中的力与位移类比推广到两个一般向量,其结果又该如何表述?
两个向量的大小及其夹角余弦的乘积
功是力与位移的大小及其夹角余弦的乘积
因为力做功的计算公式中涉及力与位移的夹角,所以我们先要定义向量的夹角概念.
探究新知
1.向量的夹角
已知两个非零向量 ,O是平面上的任意一点,作
则∠AOB=θ ( ) 叫做向量 的夹角.
O
A
B
θ
显然,当θ=0时, 同向.
当 时, 垂直,记作 .
当θ=π时, 反向.
记作:
< >
θ∈[0,π]
范围:
0≤θ≤π
课堂练习
50°
A
B
C
45°
85°
1.在△ABC中,已知A=45°,B=50°,C=85°,求下列向量的夹角:
(1)
45°
130°
85°
45°
130°
85°
(2)
(3)
问题5 两个向量的夹角与两条直线的夹角有何区别?
向量 与 之间的夹角θ的取值范围是[0, π],
注意: 必须共起点.
两直线夹角的范围 是不一样的(向量有方向).
可以平移实现.
探究新知
2.平面向量数量积的定义
已知非零向量 与 ,它们的夹角为θ,我们把数量 叫作
与 的数量积(或内积),记作 ,即规定
规定:零向量与任意向量的数量积为0,即
向量的数量积是一个数量
②一种新的运算.
①“·”不能省略不写,也不能写成“×”.
③数量积a·b的结果为实数,不是向量.(数量积运算是非线性运算)
注意:
例题讲解
例1 已知
解:
例2
解:
由 ,得
∵ ∴ .
知三求一
课堂练习
B
C
C
>
4.已知|a|=6,|b|=8,a与b平行,求a b .
探究新知
问题6 向量的数量积是一个数量,那么它什么时候为正,什么时候为负?
0°≤θ<90°
=90°
④两个非零向量的数量积,符号由夹角θ决定:
注意:
当 a·b=0时,夹角θ_______.
当 a·b>0时,夹角θ范围是_______________;
当 a·b<0时,夹角θ范围是_______________;
90°<θ ≤180°
是非零向量
⑤
探究新知
3.投影向量
设 是两个非零向量, ,过 的起点A和终点B,分别作 所在直线的垂线,垂足分别为A1,B1,得到 ,我们称这种变换为向量 向向量 投影, 叫做向量 在向量 上的投影向量.
我们可以在平面内任取一点O,作 .过点M作直线ON 的垂线,垂足为 ,则 就是向量 在向量 上的投影向量
探究新知
问题7 如图,设与 方向相同的单位向量为 , 与 的夹角为θ,那么 与 , ,θ之间有怎样的关系?
显然 与 共线,于是
所以
当θ为直角时,λ=0,所以
当θ为锐角时,与 方向相同,
探究新知
所以
当θ为钝角时,与 方向相反,
当θ=0时,λ= ,所以
当θ= 时,λ= ,所以
综上可知,对任意的 都有:
例题讲解
例题讲解
例5
课堂练习
【练习】
1.已知a,b满足|a|=2,|b|=1,且a与b的夹角为30°,那么a·b等于____.
2.已知向量a,b满足|a|=1,|b|=4,且a·b=2,则a与b的夹角θ为 .
3.已知e为单位向量,|a|=4,a与e夹角为120°,则a在e方向上的投影向量为 .
探究新知
4.数量积的性质
(3) 当 与 同向时, ;当 与 反向时, .
特别地, 或 .
(由|cosθ|≤1得到)
设a,b是非零向量,它们的夹角是θ,e是与b方向相同的单位向量,则
a a常记为a
可用于求向量的模.
(5)cosθ= .
实质是平面向量数量积的逆用,可用于求两向量的夹角,也称为夹角公式.
课堂小结
1.知识点:
(1)向量的夹角.
(2)向量数量积的定义.
(3)投影向量.
(4)向量数量积的性质.
2.方法归纳:数形结合.
3.易错点:向量夹角共起点;
a·b>0 两向量夹角为锐角,a·b<0 两向量夹角为钝角.
课堂小结
向量数量积
向量
布置作业
(1)教材
(2)同步作业
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
