青岛版(五四制)2023年数学四年级下册期末测试卷(二)(含解析)
文档属性
| 名称 | 青岛版(五四制)2023年数学四年级下册期末测试卷(二)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 210.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-07 00:00:00 | ||
图片预览


文档简介
青岛版(五四制)2023年数学四年级下册期末测试卷(二)
一、认真思考,仔细填空(30分)
1.如果小明往前走6步记作+6步,那么小明往后退12步应记作 步。
2.在1、2、4、9、18、23、56、91中,奇数有 ,偶数有 ,质数有 ,合数有 。
3.36和48的最大公因数是 ,最小公倍数是 。
4.1的分数单位是 ,它有 个这样的分数单位,再添上 个这样的分数单位就等于最小的质数。
5. = =18÷ = (填小数)。
6.比较大小。
4 3.5
7.在横线上填上合适的最简分数。
40秒= 分 50公顷= 平方千米
8角= 元 250千克= 吨
8.一个三位数□1□,既是2和3的倍数,又是5的倍数,这个数最小是 ,最大是 。
9.把56分解质因数是:56= 。
10.3个同学排成一行表演节目,可以有 种不同的排法。
11.把10吨沙子平均分4次运完,每次运这些沙子的 ,每次运 吨。
12.一个直角三角形的两条直角边分别是0.3cm和0.4cm,斜边长0.5cm,这个直角三角形的面积是 平方厘米。
13.一个平行四边形的面积是9.2平方分米,高是4分米,底是 分米。与这个平行四边形等底等高的三角形的面积是 平方分米。
二、仔细推敲,合理选择(6分)
14.一个三角形的面积是40平方厘米,高是8厘米。它的底是( )厘米。
A.5 B.10 C.15
15. 的分母增加14,要使这个分数的大小不变,分子应( )。
A.增加14 B.增加4 C.乘2
16.一个正方形的边长是一个质数,这个正方形的周长数一定是( )。
A.合数 B.奇数 C.质数
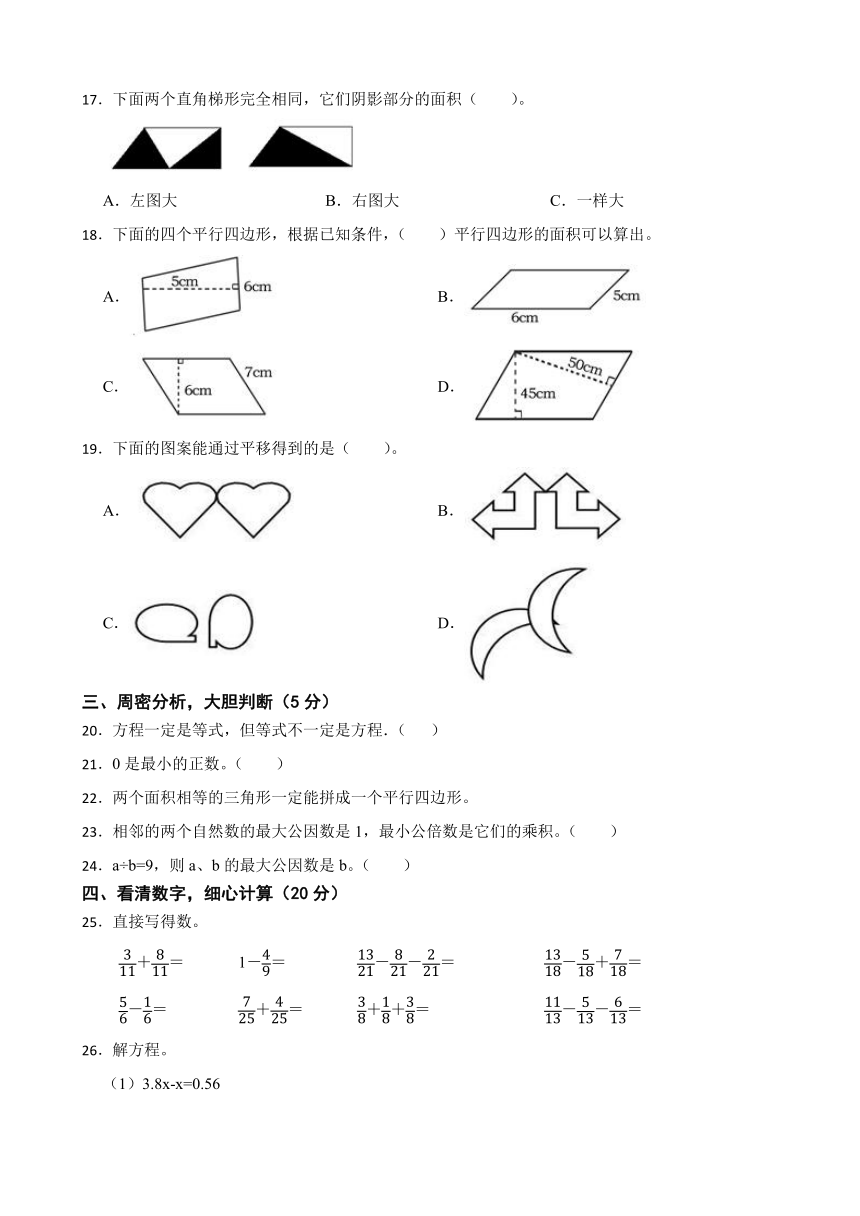
17.下面两个直角梯形完全相同,它们阴影部分的面积( )。
A.左图大 B.右图大 C.一样大
18.下面的四个平行四边形,根据已知条件,( )平行四边形的面积可以算出。
A. B.
C. D.
19.下面的图案能通过平移得到的是( )。
A. B.
C. D.
三、周密分析,大胆判断(5分)
20.方程一定是等式,但等式不一定是方程.(
)
21.0是最小的正数。( )
22.两个面积相等的三角形一定能拼成一个平行四边形。
23.相邻的两个自然数的最大公因数是1,最小公倍数是它们的乘积。( )
24.a÷b=9,则a、b的最大公因数是b。( )
四、看清数字,细心计算(20分)
25.直接写得数。
+= 1-= --= -+=
-= += ++= --=
26.解方程。
(1)3.8x-x=0.56
(2)7x+5.3=7.4
27.看图列出方程并解答。
(1)
(2)
五、观察操作,分析作答(12分)
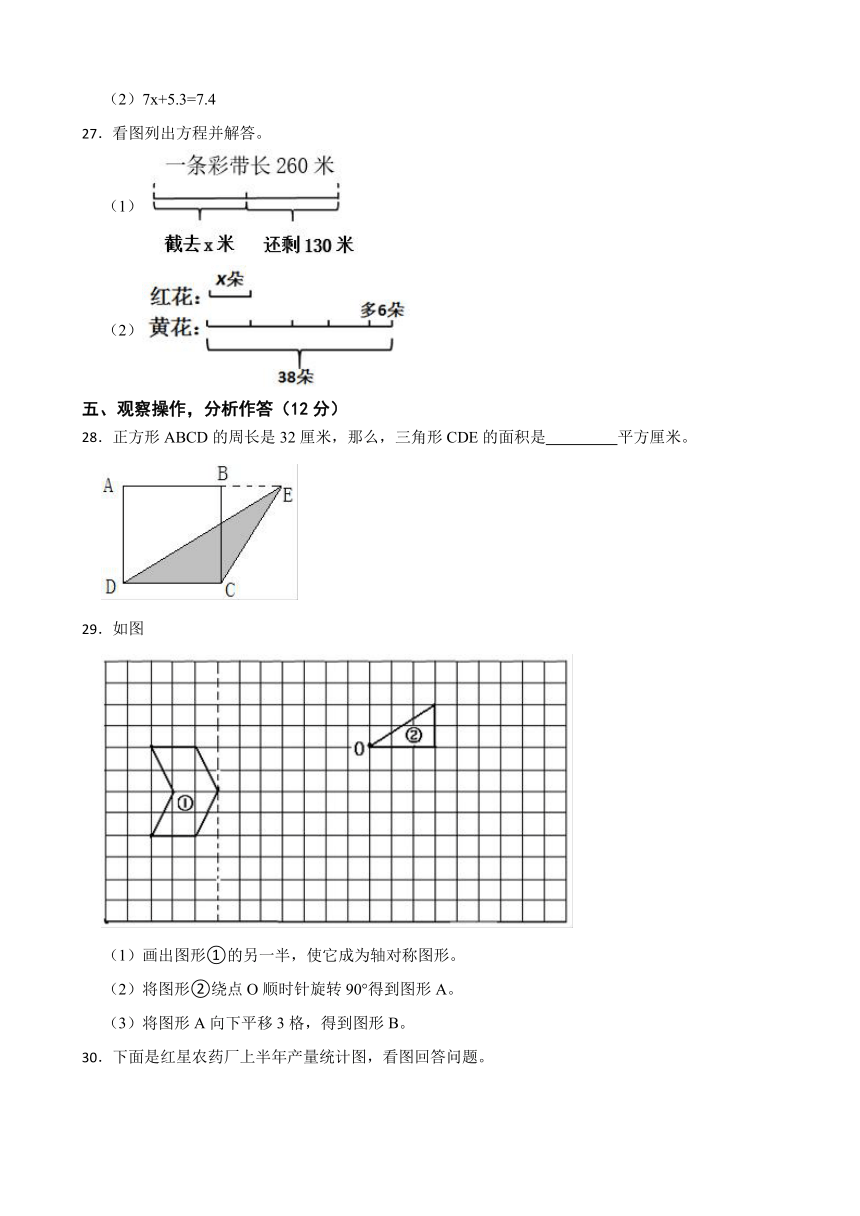
28.正方形ABCD的周长是32厘米,那么,三角形CDE的面积是 平方厘米。
29.如图
(1)画出图形①的另一半,使它成为轴对称图形。
(2)将图形②绕点O顺时针旋转90°得到图形A。
(3)将图形A向下平移3格,得到图形B。
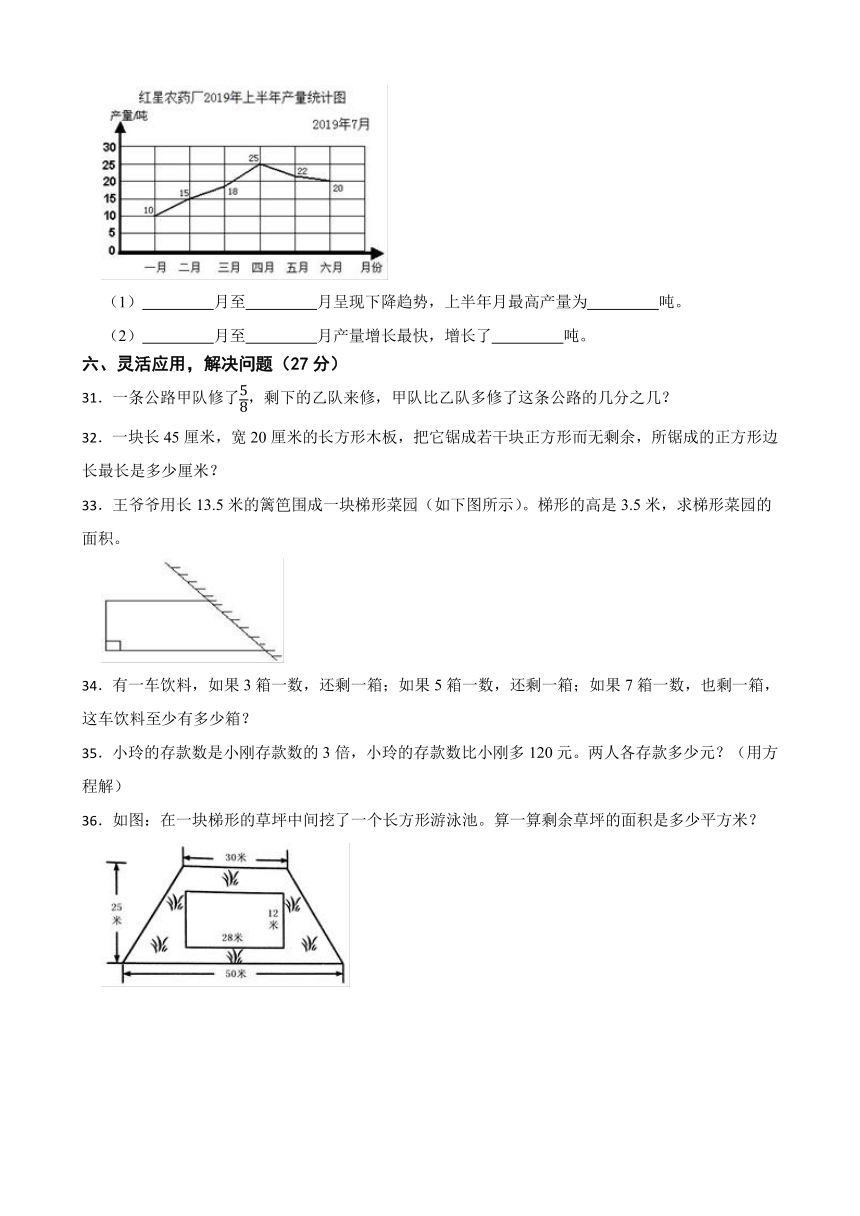
30.下面是红星农药厂上半年产量统计图,看图回答问题。
(1) 月至 月呈现下降趋势,上半年月最高产量为 吨。
(2) 月至 月产量增长最快,增长了 吨。
六、灵活应用,解决问题(27分)
31.一条公路甲队修了,剩下的乙队来修,甲队比乙队多修了这条公路的几分之几?
32.一块长45厘米,宽20厘米的长方形木板,把它锯成若干块正方形而无剩余,所锯成的正方形边长最长是多少厘米?
33.王爷爷用长13.5米的篱笆围成一块梯形菜园(如下图所示)。梯形的高是3.5米,求梯形菜园的面积。
34.有一车饮料,如果3箱一数,还剩一箱;如果5箱一数,还剩一箱;如果7箱一数,也剩一箱,这车饮料至少有多少箱?
35.小玲的存款数是小刚存款数的3倍,小玲的存款数比小刚多120元。两人各存款多少元?(用方程解)
36.如图:在一块梯形的草坪中间挖了一个长方形游泳池。算一算剩余草坪的面积是多少平方米?
答案解析部分
1.【答案】-12
【知识点】正、负数的意义与应用
【解析】【解答】解:小明往后退12步应记作-12步。
故答案为:-12。
【分析】往前走用正数表示,往后退用负数表示。
2.【答案】1、9、23、91;2、4、18、56;2、23;4、9、18、56、91
【知识点】奇数和偶数;合数与质数的特征
【解析】【解答】解:奇数有1、9、23、91;
偶数有2、4、18、56;
质数有2、23;
合数有4、9、18、56、91。
故答案为:1、9、23、91;2、4、18、56;2、23;4、9、18、56、91。
【分析】不能被2整除的数是奇数,能被2整除的数是偶数;一个数,如果只有1和它本身两个因数,这样的数叫做质数;一个数,除了1和它本身还有别的因数,这样的数叫做合数。
3.【答案】12;144
【知识点】公因数与最大公因数;公倍数与最小公倍数
【解析】【解答】解:36=12×3,48=12×4,
36和48的最大公因数是12,最小公倍数是12×3×4=144。
故答案为:12;144。
【分析】两个数的最大公因数是把这两个数公有的质因数相乘;两个数的最小公倍数是把这两个数公有的质因数和它们各自独有的质因数相乘。
4.【答案】;13;4
【知识点】分数单位的认识与判断
【解析】【解答】解:最小的质数是2,2=,-1=;
1的分数单位是,它有13个这样的分数单位,再添上5个这样的分数单位就等于最小的质数。
故答案为:;13;4。
【分析】一个分数的分数单位就是分母分之一,它有分子个这样的分数单位。
5.【答案】12;24;0.75
【知识点】分数与除法的关系;分数与小数的互化
【解析】【解答】解:9÷=12;18÷=24;=3÷4=0.75。
故答案为:12;24;0.75。
【分析】分母=分子÷分数值;除数=被除数÷商;分数化小数:用分子除以分母,商写成小数的形式。
6.【答案】=;>;>;<
【知识点】异分子分母分数大小比较;分数与小数的大小比较
【解析】【解答】解:=48÷12=4;
>1,<1,所以>;
>;
=19÷6≈3.2,3.5<。
故答案为:=;>;>;<。
【分析】同分母分数比较大小,分子越大,这个分数就越大;分子和分母都不相同的分数比较大小,可以化为同分母分数比较大小,也可以都化为小数再比较大小。
7.【答案】;;;
【知识点】除数是整数的分数除法
【解析】【解答】解:40秒÷60=分;50公顷÷100=平方千米;
8角÷10=元;250千克÷1000=吨。
故答案为:;;;。
【分析】被除数÷除数=商写成分数的形式,分子是被除数,分母是除数。
8.【答案】210;810
【知识点】2、5的倍数的特征;3的倍数的特征
【解析】【解答】解:同时是2、5的倍数说明个位上的数字是0;
既是2和3的倍数,又是5的倍数,这个数最小是210,最大是810。
故答案为:210;810。
【分析】同时是2、3、5的倍数的数的特征是这个数个位上的数字是0,所有数位上的数字之和是3的倍数。
9.【答案】56=2×2×2×7
【知识点】分解质因数
【解析】【解答】解:56=2×2×2×7。
故答案为:56=2×2×2×7。
【分析】把一个合数分解成若干个质数的乘积的形式,叫做分解质因数。
10.【答案】6
【知识点】排列组合
【解析】【解答】解:可以有6种不同的排法。
故答案为:6。
【分析】可以有123、132、231、213、312、312,据此解答。
11.【答案】;2.5
【知识点】除数是整数的分数除法
【解析】【解答】解:每次运这些沙子的1÷4=;
每次运10÷4=2.5(吨)。
故答案为:;2.5。
【分析】单位1÷运完的次数=每次运这些沙子的分率;沙子吨数÷运的次数=每次运的吨数。
12.【答案】0.06
【知识点】三角形的面积
【解析】【解答】解:0.3×0.4÷2=0.06(平方厘米)
故答案为:0.06。
【分析】直角三角形的两条直角边的积,就是这个直角三角形的面积。
13.【答案】2.3;4.6
【知识点】平行四边形的面积;三角形的面积
【解析】【解答】解:9.2÷4=2.3(分米)
9.2÷2=4.6(平方分米)
故答案为:2.3;4.6。
【分析】平行四边形的面积÷底=高;等底等高的三角形的面积是平行四边形面积的一半。
14.【答案】B
【知识点】三角形的面积
【解析】【解答】解:40×2÷8=10(厘米)
故答案为:B。
【分析】三角形面积×2÷高=底。
15.【答案】B
【知识点】分数的基本性质
【解析】【解答】解:14÷7=2;分子增加2×2=4。
故答案为:B。
【分析】分母增加2倍,要使这个分数的大小不变,分子应增加2倍,2的2倍是4。
16.【答案】A
【知识点】合数与质数的特征
【解析】【解答】解:正方形的边长×4=这个正方形的周长;即质数×4一定是合数。
故答案为:A。
【分析】一个数,如果只有1和它本身两个因数,这样的数叫做质数;一个数,除了1和它本身还有别的因数,这样的数叫做合数。
17.【答案】C
【知识点】组合图形面积的巧算;三角形的面积;梯形的特征及分类
【解析】【解答】解:它们阴影部分的面积一样大。
故答案为:C。
【分析】两个空白三角形等底等高,两个空白三角形的面积相等;所以它们阴影部分的面积也相等。
18.【答案】A
【知识点】平行四边形的面积
【解析】【解答】解:第一个图形平行四边形的面积可以算出。
故答案为:A。
【分析】平行四边形的面积=平行四边形的底×底边上的高。
19.【答案】A
【知识点】平移与平移现象
【解析】【解答】解:第一个图形能通过平移得到。
故答案为:A。
【分析】平移:物体或图形沿着某个方向移动了一定距离叫做平移。特点:大小、形状、方向不变,位置变化。
20.【答案】(1)正确
【知识点】方程的认识及列简易方程
【解析】【解答】解:方程一定是等式,但等式不一定是方程。原题说法正确。
故答案为:正确。
【分析】含有未知数的等式叫做方程,所以方程一定是等式,等式不一定是方程。
21.【答案】(1)错误
【知识点】正、负数的认识与读写
【解析】【解答】解:0不是正数。原题说法错误。
故答案为:错误。
【分析】大于0的数是正数,小于0的数是负数,0不是正数,也不是负数。
22.【答案】(1)错误
【知识点】平行四边形的特征及性质
【解析】【解答】解:例如:底边长为4,高为3和底边长为2,高为6的两个三角形,面积相等,但是不能拼成平行四边形.
面积相等的两个三角形一定能拼成平行四边形,说法错误.
故答案为:错误.
【分析】因为只有完全一样的三角形才可以,面积相等的三角形,未必底边和高分别相等,据此举例说明即可判断.此题应认真进行分析,通过举例进行验证,故而得出问题答案.
23.【答案】(1)正确
【知识点】公因数与最大公因数;互质数的特征;公倍数与最小公倍数
【解析】【解答】解:相邻的两个自然数的最大公因数是1,最小公倍数是它们的乘积。说法正确。
故答案为:正确。
【分析】相邻的两个自然数是互质数;两个数是互质数,最大公因数是1,最小公倍数是它们的积。
24.【答案】(1)正确
【知识点】公因数与最大公因数
【解析】【解答】解:a÷b=9,a、b是倍数关系;则a、b的最大公因数是b。说法正确。
故答案为:正确。
【分析】两个数成倍数关系,最大公因数是较小的数,最小公倍数是较大的数。
25.【答案】
+=1 1-= --= -+=
-= += ++= --=0
【知识点】同分母分数加减法;分数加减混合运算及应用
【解析】【分析】同分母分数相加减,分母不变,分子相加减。计算的结果,能约分的要约成最简分数。
26.【答案】(1)解:3.8x-x=0.56
2.8x=0.56
x=0.56÷2.8
x=0.2
(2)解:7x+5.3=7.4
7x=7.4-5.3
7x=2.1
x=2.1÷7
x=0.3
【知识点】综合应用等式的性质解方程
【解析】【分析】综合运用等式性质解方程;
等式性质1:等式两边加上或减去同一个数,左右两边仍然相等;
等式性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
27.【答案】(1)解:x+130=260
x=260-130
x=130
答:截去130米。
(2)解:4x+6=38
4x=38-6
4x=32
x=32÷4
x=8
答:红花的8朵。
【知识点】列方程解含有一个未知数的应用题
【解析】【分析】(1)截去的长度+还剩的长度=260米,根据等量关系列方程,根据等式性质解方程。
(2)红花的朵数×4+6朵=38朵,根据等量关系列方程,根据等式性质解方程。
28.【答案】32
【知识点】三角形的面积
【解析】【解答】解:32÷4=8(厘米)
8×8÷2=32(平方厘米)
故答案为:32。
【分析】正方形的周长÷4=正方形的边长;三角形的底和高都等于正方形的边长;三角形的底×高÷2=三角形的面积。
29.【答案】(1)解:
(2)解:
(3)解:
【知识点】补全轴对称图形;作平移后的图形;作旋转后的图形
【解析】【分析】(1)补全轴对称图形方法:根据对称点到对称轴的距离相等,找出各个关键点的对称点,然后再连线;
(2)旋转画法:旋转后图形的位置改变,转动的中心点、形状、大小不变。因此画图时,先弄清楚旋转的方向和角度,找准关键线段旋转后的位置,据此作图即可;
(3)平移画法:先把图形中的关键点都按题干要求的方向和格数移动,然后再连接各点。
30.【答案】(1)4;6;25
(2)3;4;7
【知识点】从单式折线统计图获取信息
【解析】【解答】解:(1)4月至6月呈现下降趋势,上半年月最高产量为25吨;
(2)3月至4月产量增长最快,增长了25-18=7(吨)。
故答案为:(1)4;6;25;(2)3;4;7。
【分析】(1)4月至6月折线开始向下走,说明呈现下降趋势;
(2)3月至4月产量增长了1格多,增长的最快。
31.【答案】解:-(1-)
=-
=
答:甲队比乙队多修了这条公路的。
【知识点】分数加减混合运算及应用
【解析】【分析】单位1-甲队修的几分之几=乙队修的几分之几,甲队修的几分之几-乙队修的几分之几=甲队比乙队多修了这条公路的几分之几。
32.【答案】5厘米
【知识点】最大公因数的应用
【解析】【解答】45的因数:1、3、5、9、15、45
20的因数:1、2、4、5、10、20
【分析】因为切成正方形,正方形的特点是4条边都是相等的,所以最长应该是5厘米。
33.【答案】解:(13.5-3.5)×3.5÷2
=10×3.5÷2
=17.5(平方米)
答:梯形菜园的面积是17.5平方米。
【知识点】梯形的面积
【解析】【分析】篱笆的长-3.5米=梯形的上下底之和,梯形的上下底之和×高÷2=梯形面积。
34.【答案】106
【知识点】最小公倍数的应用
【解析】【解答】3×5×7+1=106
【分析】假设,先不考虑多一箱的情况,这车饮料的箱数,是3的倍数,又是5的倍数,还是7的倍数,但是3、5、7相互之间,又没有因数和倍数的关系,所以最小的数就应该是3×5×7=105,再加上一箱,就应该是106箱。
35.【答案】解:设小刚存款数是x元,则小玲的存款数是3x元。
3x-x=120
2x=120
x=60
60×3=180(元)
答:小刚存款数是60元,则小玲的存款数是180元。
【知识点】列方程解含有多个未知数的应用题
【解析】【分析】等量关系:小玲的存款数-小刚存款数=120,根据等量关系列方程,根据等式性质解方程。
36.【答案】解:(30+50)×25÷2-28×12
=80×25÷2-28×12
=1000-336
=664(平方米)
答:剩余草坪的面积是664平方米。
【知识点】梯形的面积;长方形的面积
【解析】【分析】(上底+下底)×高÷2=梯形面积,长×宽=长方形面积,梯形面积-长方形面积=草坪的面积。
一、认真思考,仔细填空(30分)
1.如果小明往前走6步记作+6步,那么小明往后退12步应记作 步。
2.在1、2、4、9、18、23、56、91中,奇数有 ,偶数有 ,质数有 ,合数有 。
3.36和48的最大公因数是 ,最小公倍数是 。
4.1的分数单位是 ,它有 个这样的分数单位,再添上 个这样的分数单位就等于最小的质数。
5. = =18÷ = (填小数)。
6.比较大小。
4 3.5
7.在横线上填上合适的最简分数。
40秒= 分 50公顷= 平方千米
8角= 元 250千克= 吨
8.一个三位数□1□,既是2和3的倍数,又是5的倍数,这个数最小是 ,最大是 。
9.把56分解质因数是:56= 。
10.3个同学排成一行表演节目,可以有 种不同的排法。
11.把10吨沙子平均分4次运完,每次运这些沙子的 ,每次运 吨。
12.一个直角三角形的两条直角边分别是0.3cm和0.4cm,斜边长0.5cm,这个直角三角形的面积是 平方厘米。
13.一个平行四边形的面积是9.2平方分米,高是4分米,底是 分米。与这个平行四边形等底等高的三角形的面积是 平方分米。
二、仔细推敲,合理选择(6分)
14.一个三角形的面积是40平方厘米,高是8厘米。它的底是( )厘米。
A.5 B.10 C.15
15. 的分母增加14,要使这个分数的大小不变,分子应( )。
A.增加14 B.增加4 C.乘2
16.一个正方形的边长是一个质数,这个正方形的周长数一定是( )。
A.合数 B.奇数 C.质数
17.下面两个直角梯形完全相同,它们阴影部分的面积( )。
A.左图大 B.右图大 C.一样大
18.下面的四个平行四边形,根据已知条件,( )平行四边形的面积可以算出。
A. B.
C. D.
19.下面的图案能通过平移得到的是( )。
A. B.
C. D.
三、周密分析,大胆判断(5分)
20.方程一定是等式,但等式不一定是方程.(
)
21.0是最小的正数。( )
22.两个面积相等的三角形一定能拼成一个平行四边形。
23.相邻的两个自然数的最大公因数是1,最小公倍数是它们的乘积。( )
24.a÷b=9,则a、b的最大公因数是b。( )
四、看清数字,细心计算(20分)
25.直接写得数。
+= 1-= --= -+=
-= += ++= --=
26.解方程。
(1)3.8x-x=0.56
(2)7x+5.3=7.4
27.看图列出方程并解答。
(1)
(2)
五、观察操作,分析作答(12分)
28.正方形ABCD的周长是32厘米,那么,三角形CDE的面积是 平方厘米。
29.如图
(1)画出图形①的另一半,使它成为轴对称图形。
(2)将图形②绕点O顺时针旋转90°得到图形A。
(3)将图形A向下平移3格,得到图形B。
30.下面是红星农药厂上半年产量统计图,看图回答问题。
(1) 月至 月呈现下降趋势,上半年月最高产量为 吨。
(2) 月至 月产量增长最快,增长了 吨。
六、灵活应用,解决问题(27分)
31.一条公路甲队修了,剩下的乙队来修,甲队比乙队多修了这条公路的几分之几?
32.一块长45厘米,宽20厘米的长方形木板,把它锯成若干块正方形而无剩余,所锯成的正方形边长最长是多少厘米?
33.王爷爷用长13.5米的篱笆围成一块梯形菜园(如下图所示)。梯形的高是3.5米,求梯形菜园的面积。
34.有一车饮料,如果3箱一数,还剩一箱;如果5箱一数,还剩一箱;如果7箱一数,也剩一箱,这车饮料至少有多少箱?
35.小玲的存款数是小刚存款数的3倍,小玲的存款数比小刚多120元。两人各存款多少元?(用方程解)
36.如图:在一块梯形的草坪中间挖了一个长方形游泳池。算一算剩余草坪的面积是多少平方米?
答案解析部分
1.【答案】-12
【知识点】正、负数的意义与应用
【解析】【解答】解:小明往后退12步应记作-12步。
故答案为:-12。
【分析】往前走用正数表示,往后退用负数表示。
2.【答案】1、9、23、91;2、4、18、56;2、23;4、9、18、56、91
【知识点】奇数和偶数;合数与质数的特征
【解析】【解答】解:奇数有1、9、23、91;
偶数有2、4、18、56;
质数有2、23;
合数有4、9、18、56、91。
故答案为:1、9、23、91;2、4、18、56;2、23;4、9、18、56、91。
【分析】不能被2整除的数是奇数,能被2整除的数是偶数;一个数,如果只有1和它本身两个因数,这样的数叫做质数;一个数,除了1和它本身还有别的因数,这样的数叫做合数。
3.【答案】12;144
【知识点】公因数与最大公因数;公倍数与最小公倍数
【解析】【解答】解:36=12×3,48=12×4,
36和48的最大公因数是12,最小公倍数是12×3×4=144。
故答案为:12;144。
【分析】两个数的最大公因数是把这两个数公有的质因数相乘;两个数的最小公倍数是把这两个数公有的质因数和它们各自独有的质因数相乘。
4.【答案】;13;4
【知识点】分数单位的认识与判断
【解析】【解答】解:最小的质数是2,2=,-1=;
1的分数单位是,它有13个这样的分数单位,再添上5个这样的分数单位就等于最小的质数。
故答案为:;13;4。
【分析】一个分数的分数单位就是分母分之一,它有分子个这样的分数单位。
5.【答案】12;24;0.75
【知识点】分数与除法的关系;分数与小数的互化
【解析】【解答】解:9÷=12;18÷=24;=3÷4=0.75。
故答案为:12;24;0.75。
【分析】分母=分子÷分数值;除数=被除数÷商;分数化小数:用分子除以分母,商写成小数的形式。
6.【答案】=;>;>;<
【知识点】异分子分母分数大小比较;分数与小数的大小比较
【解析】【解答】解:=48÷12=4;
>1,<1,所以>;
>;
=19÷6≈3.2,3.5<。
故答案为:=;>;>;<。
【分析】同分母分数比较大小,分子越大,这个分数就越大;分子和分母都不相同的分数比较大小,可以化为同分母分数比较大小,也可以都化为小数再比较大小。
7.【答案】;;;
【知识点】除数是整数的分数除法
【解析】【解答】解:40秒÷60=分;50公顷÷100=平方千米;
8角÷10=元;250千克÷1000=吨。
故答案为:;;;。
【分析】被除数÷除数=商写成分数的形式,分子是被除数,分母是除数。
8.【答案】210;810
【知识点】2、5的倍数的特征;3的倍数的特征
【解析】【解答】解:同时是2、5的倍数说明个位上的数字是0;
既是2和3的倍数,又是5的倍数,这个数最小是210,最大是810。
故答案为:210;810。
【分析】同时是2、3、5的倍数的数的特征是这个数个位上的数字是0,所有数位上的数字之和是3的倍数。
9.【答案】56=2×2×2×7
【知识点】分解质因数
【解析】【解答】解:56=2×2×2×7。
故答案为:56=2×2×2×7。
【分析】把一个合数分解成若干个质数的乘积的形式,叫做分解质因数。
10.【答案】6
【知识点】排列组合
【解析】【解答】解:可以有6种不同的排法。
故答案为:6。
【分析】可以有123、132、231、213、312、312,据此解答。
11.【答案】;2.5
【知识点】除数是整数的分数除法
【解析】【解答】解:每次运这些沙子的1÷4=;
每次运10÷4=2.5(吨)。
故答案为:;2.5。
【分析】单位1÷运完的次数=每次运这些沙子的分率;沙子吨数÷运的次数=每次运的吨数。
12.【答案】0.06
【知识点】三角形的面积
【解析】【解答】解:0.3×0.4÷2=0.06(平方厘米)
故答案为:0.06。
【分析】直角三角形的两条直角边的积,就是这个直角三角形的面积。
13.【答案】2.3;4.6
【知识点】平行四边形的面积;三角形的面积
【解析】【解答】解:9.2÷4=2.3(分米)
9.2÷2=4.6(平方分米)
故答案为:2.3;4.6。
【分析】平行四边形的面积÷底=高;等底等高的三角形的面积是平行四边形面积的一半。
14.【答案】B
【知识点】三角形的面积
【解析】【解答】解:40×2÷8=10(厘米)
故答案为:B。
【分析】三角形面积×2÷高=底。
15.【答案】B
【知识点】分数的基本性质
【解析】【解答】解:14÷7=2;分子增加2×2=4。
故答案为:B。
【分析】分母增加2倍,要使这个分数的大小不变,分子应增加2倍,2的2倍是4。
16.【答案】A
【知识点】合数与质数的特征
【解析】【解答】解:正方形的边长×4=这个正方形的周长;即质数×4一定是合数。
故答案为:A。
【分析】一个数,如果只有1和它本身两个因数,这样的数叫做质数;一个数,除了1和它本身还有别的因数,这样的数叫做合数。
17.【答案】C
【知识点】组合图形面积的巧算;三角形的面积;梯形的特征及分类
【解析】【解答】解:它们阴影部分的面积一样大。
故答案为:C。
【分析】两个空白三角形等底等高,两个空白三角形的面积相等;所以它们阴影部分的面积也相等。
18.【答案】A
【知识点】平行四边形的面积
【解析】【解答】解:第一个图形平行四边形的面积可以算出。
故答案为:A。
【分析】平行四边形的面积=平行四边形的底×底边上的高。
19.【答案】A
【知识点】平移与平移现象
【解析】【解答】解:第一个图形能通过平移得到。
故答案为:A。
【分析】平移:物体或图形沿着某个方向移动了一定距离叫做平移。特点:大小、形状、方向不变,位置变化。
20.【答案】(1)正确
【知识点】方程的认识及列简易方程
【解析】【解答】解:方程一定是等式,但等式不一定是方程。原题说法正确。
故答案为:正确。
【分析】含有未知数的等式叫做方程,所以方程一定是等式,等式不一定是方程。
21.【答案】(1)错误
【知识点】正、负数的认识与读写
【解析】【解答】解:0不是正数。原题说法错误。
故答案为:错误。
【分析】大于0的数是正数,小于0的数是负数,0不是正数,也不是负数。
22.【答案】(1)错误
【知识点】平行四边形的特征及性质
【解析】【解答】解:例如:底边长为4,高为3和底边长为2,高为6的两个三角形,面积相等,但是不能拼成平行四边形.
面积相等的两个三角形一定能拼成平行四边形,说法错误.
故答案为:错误.
【分析】因为只有完全一样的三角形才可以,面积相等的三角形,未必底边和高分别相等,据此举例说明即可判断.此题应认真进行分析,通过举例进行验证,故而得出问题答案.
23.【答案】(1)正确
【知识点】公因数与最大公因数;互质数的特征;公倍数与最小公倍数
【解析】【解答】解:相邻的两个自然数的最大公因数是1,最小公倍数是它们的乘积。说法正确。
故答案为:正确。
【分析】相邻的两个自然数是互质数;两个数是互质数,最大公因数是1,最小公倍数是它们的积。
24.【答案】(1)正确
【知识点】公因数与最大公因数
【解析】【解答】解:a÷b=9,a、b是倍数关系;则a、b的最大公因数是b。说法正确。
故答案为:正确。
【分析】两个数成倍数关系,最大公因数是较小的数,最小公倍数是较大的数。
25.【答案】
+=1 1-= --= -+=
-= += ++= --=0
【知识点】同分母分数加减法;分数加减混合运算及应用
【解析】【分析】同分母分数相加减,分母不变,分子相加减。计算的结果,能约分的要约成最简分数。
26.【答案】(1)解:3.8x-x=0.56
2.8x=0.56
x=0.56÷2.8
x=0.2
(2)解:7x+5.3=7.4
7x=7.4-5.3
7x=2.1
x=2.1÷7
x=0.3
【知识点】综合应用等式的性质解方程
【解析】【分析】综合运用等式性质解方程;
等式性质1:等式两边加上或减去同一个数,左右两边仍然相等;
等式性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
27.【答案】(1)解:x+130=260
x=260-130
x=130
答:截去130米。
(2)解:4x+6=38
4x=38-6
4x=32
x=32÷4
x=8
答:红花的8朵。
【知识点】列方程解含有一个未知数的应用题
【解析】【分析】(1)截去的长度+还剩的长度=260米,根据等量关系列方程,根据等式性质解方程。
(2)红花的朵数×4+6朵=38朵,根据等量关系列方程,根据等式性质解方程。
28.【答案】32
【知识点】三角形的面积
【解析】【解答】解:32÷4=8(厘米)
8×8÷2=32(平方厘米)
故答案为:32。
【分析】正方形的周长÷4=正方形的边长;三角形的底和高都等于正方形的边长;三角形的底×高÷2=三角形的面积。
29.【答案】(1)解:
(2)解:
(3)解:
【知识点】补全轴对称图形;作平移后的图形;作旋转后的图形
【解析】【分析】(1)补全轴对称图形方法:根据对称点到对称轴的距离相等,找出各个关键点的对称点,然后再连线;
(2)旋转画法:旋转后图形的位置改变,转动的中心点、形状、大小不变。因此画图时,先弄清楚旋转的方向和角度,找准关键线段旋转后的位置,据此作图即可;
(3)平移画法:先把图形中的关键点都按题干要求的方向和格数移动,然后再连接各点。
30.【答案】(1)4;6;25
(2)3;4;7
【知识点】从单式折线统计图获取信息
【解析】【解答】解:(1)4月至6月呈现下降趋势,上半年月最高产量为25吨;
(2)3月至4月产量增长最快,增长了25-18=7(吨)。
故答案为:(1)4;6;25;(2)3;4;7。
【分析】(1)4月至6月折线开始向下走,说明呈现下降趋势;
(2)3月至4月产量增长了1格多,增长的最快。
31.【答案】解:-(1-)
=-
=
答:甲队比乙队多修了这条公路的。
【知识点】分数加减混合运算及应用
【解析】【分析】单位1-甲队修的几分之几=乙队修的几分之几,甲队修的几分之几-乙队修的几分之几=甲队比乙队多修了这条公路的几分之几。
32.【答案】5厘米
【知识点】最大公因数的应用
【解析】【解答】45的因数:1、3、5、9、15、45
20的因数:1、2、4、5、10、20
【分析】因为切成正方形,正方形的特点是4条边都是相等的,所以最长应该是5厘米。
33.【答案】解:(13.5-3.5)×3.5÷2
=10×3.5÷2
=17.5(平方米)
答:梯形菜园的面积是17.5平方米。
【知识点】梯形的面积
【解析】【分析】篱笆的长-3.5米=梯形的上下底之和,梯形的上下底之和×高÷2=梯形面积。
34.【答案】106
【知识点】最小公倍数的应用
【解析】【解答】3×5×7+1=106
【分析】假设,先不考虑多一箱的情况,这车饮料的箱数,是3的倍数,又是5的倍数,还是7的倍数,但是3、5、7相互之间,又没有因数和倍数的关系,所以最小的数就应该是3×5×7=105,再加上一箱,就应该是106箱。
35.【答案】解:设小刚存款数是x元,则小玲的存款数是3x元。
3x-x=120
2x=120
x=60
60×3=180(元)
答:小刚存款数是60元,则小玲的存款数是180元。
【知识点】列方程解含有多个未知数的应用题
【解析】【分析】等量关系:小玲的存款数-小刚存款数=120,根据等量关系列方程,根据等式性质解方程。
36.【答案】解:(30+50)×25÷2-28×12
=80×25÷2-28×12
=1000-336
=664(平方米)
答:剩余草坪的面积是664平方米。
【知识点】梯形的面积;长方形的面积
【解析】【分析】(上底+下底)×高÷2=梯形面积,长×宽=长方形面积,梯形面积-长方形面积=草坪的面积。
同课章节目录
