九年级数学上册试题 4.1成比例线段--黄金分割同步练习 北师大版(含答案)
文档属性
| 名称 | 九年级数学上册试题 4.1成比例线段--黄金分割同步练习 北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 500.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-09 13:49:15 | ||
图片预览




文档简介
4.1成比例线段--黄金分割
一、单选题
1.生活中到处可见黄金分割的美.如图,点C将线段AB分成AC、CB两部分,且AC>BC,如果,那么称点C为线段AB的黄金分割点.若C是线段AB的黄金分割点,AB=2,则分割后较短线段长为( )
A. B. C. D.
2.世界上最有名的建筑物中几乎都包含“黄金分割”,如成都广播电视塔同样蕴含着“黄金分割”,如图,塔高AB为339米,观光区P为塔AB的黄金分割点(AP>PB),那么AP的高度大约为( )米.
A.200 B.210 C.300 D.130
3.点是线段的黄金分割点,且,则的长为( )
A. B.
C.或 D.或
4.已知点是线段的黄金分割点,,则的值为( )
A. B. C.0.618 D.
5.如图,线段AB=1,点P1是线段AB的黄金分割点(且AP1<BP1,即P1B2=AP1 AB),点P2是线段AP1的黄金分割点(AP2<P1P2),点P3是线段AP2的黄金分割点(AP3<P2P3),…,依此类推,则线段AP2017的长度是( )
A.()2017 B.()2017 C.()2017 D.(﹣2)1008
6.古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段分为两线段,,使得其中较长的一段是全长与较短的段的比例中项,即满足,后人把这个数称为“黄金分割”数,把点G称为线段的“黄金分割”点.如图,在中,已知,,若D,E是边的两个“黄金分割”点,则的面积为( )
A. B. C. D.
7.有以下命题:
①如果线段是线段,,的第四比例项,则有;
②如果点是线段的中点,那么是、的比例中项;
③如果点是线段的黄金分割点,且,那么是与的比例中项;
④如果点是线段的黄金分割点,,且,则.
其中正确的判断有( )
A.②④ B.①②③④ C.①③④ D.②③④
8.采用如下方法可以得到线段的黄金分割点:如图,设AB是已知线段,经过点B做BD⊥AB,使;连接DA,在DA上取DE=DB,在AB上截取AC=AE.点C即为线段AB的黄金分割点,若BD=2,则BC的长为( )
A. B. C. D.
9.古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是(,称为黄金分割比例),如图,著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是.若某人满足上述两个黄金分割比例,且腿长为,头顶至脖子下端的长度为,则其身高可能是( )
A. B. C. D.
二、填空题
10.大自然巧夺天工,一片小小树叶,也蕴含着“黄金分割”.如图,为的黄金分割点,如果的长度为,那么的长度是______.
11.人们把这个数叫做黄金分割数,著名数学家华罗庚优选法中的法就应用了黄金分割数.设,,则,记,,…,.则____.
12.点是线段的黄金分割点,,若,则__.
13.如图,线段AB=1,点P1是线段AB的黄金分割点(AP114.大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”.如图,为的黄金分割点,如果的长度为,那么的长度是_____________.
15.已知线段,点c是线段的黄金分割点,.那么________.
16.“黄金分割”被视为最美丽的几何学比率,在建筑、艺术和日常生活中处处可见.如图,D、E是△ABC中边BC的两个“黄金分割”点,则△ADE与△ABC的面积之比是_____.
17.若线段,是的黄金分割点,且,则AC=
18.已知点为线段的黄金分割点,且,则线段的长为________.
19.点 C 是线段 AB 的黄金分割点(AC>BC),若 AC=2则 =______.
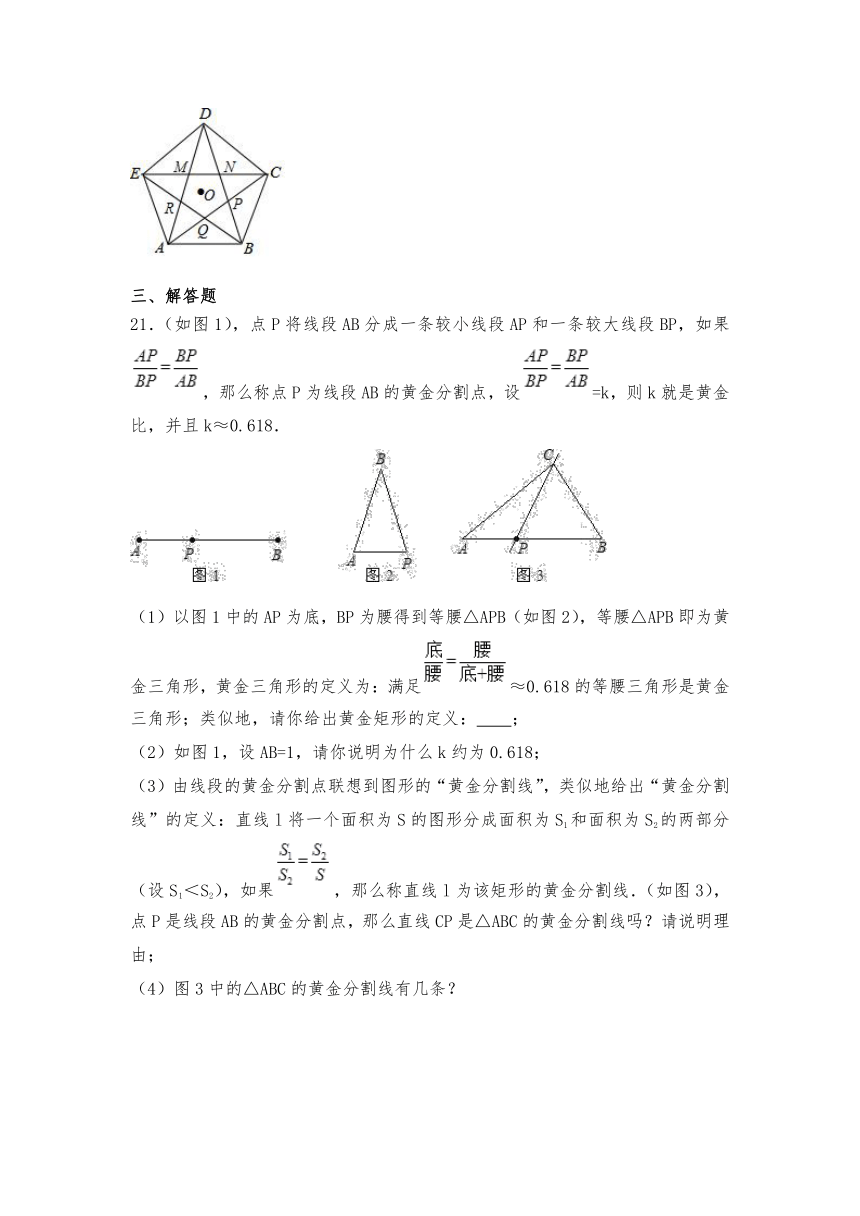
20.如图,正五边形ABCDE的各条对角线的交点为M,N,P,Q,R,它们分别是各条对角线的黄金分割点.若AB=2,则MN的长为__.
三、解答题
21.(如图1),点P将线段AB分成一条较小线段AP和一条较大线段BP,如果,那么称点P为线段AB的黄金分割点,设=k,则k就是黄金比,并且k≈0.618.
(1)以图1中的AP为底,BP为腰得到等腰△APB(如图2),等腰△APB即为黄金三角形,黄金三角形的定义为:满足≈0.618的等腰三角形是黄金三角形;类似地,请你给出黄金矩形的定义: ;
(2)如图1,设AB=1,请你说明为什么k约为0.618;
(3)由线段的黄金分割点联想到图形的“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成面积为S1和面积为S2的两部分(设S1<S2),如果,那么称直线l为该矩形的黄金分割线.(如图3),点P是线段AB的黄金分割点,那么直线CP是△ABC的黄金分割线吗?请说明理由;
(4)图3中的△ABC的黄金分割线有几条?
22.如图1所示,点C将线段AB分成两部分,如果,那么点C为线段AB的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2,如果,那么称直线l为该图形的黄金分割线.
(1)研究小组猜想:在△ABC中,若点D为AB边上的黄金分割点,如图2所示,则直线CD是△ABC的黄金分割线,你认为对吗?说说你的理由;
(2)请你说明:三角形的中线是否是该三角形的黄金分割线.
23.如图①,点C将线段分成两部分,如果,那么称点C为线段的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为,,如果,那么称直线l为该图形的黄金分割线.
(1)研究小组猜想:在中,若点D为边上的黄金分割点(如图②),则直线是的黄金分割线.你认为对吗?为什么?
(2)请你说明:三角形的中线是否也是该三角形的黄金分割线?
(3)在(1)中的中,研究小组在进一步探究中发现:过点C任作一条直线交于点E,再过点D作直线,交AC于点F,连接(如图③),则直线也是的黄金分割线.请你说明理由;
(4)如图④,点E是平行四边形的边的黄金分割点,过点E作,交于点F,显然直线是平行四边形的黄金分割线.请你画一条平行四边形的黄金分割线,使它不经过平行四边形各边黄金分割点.
24.一般地,点把线段分成两条线段和,如果,那么称线段被点黄金分割,点叫做线段的黄金分割点,与的比叫做黄金比.请计算黄金比.
25.阅读与思考
黄金分割
黄金分割起源于古希腊的毕达哥拉斯学派,公元前4世纪,古希腊数学家欧多克索斯第一个系统研究了黄金分割比例这一问题,并建立起比例理论.后来欧几里得进一步系统论述了黄金分割,其《几何原本》成为最早的有关黄金分割的论著.黄金分割指的是把一条线段分成两部分,使其中较长部分与线段总长之比等于较短部分与较长部分之比.
黄金分割在美学、艺术、建筑和日常生活方面有看广泛的应用.如埃及的金字塔、印度的泰姬陵等,都可发现与黄金比有联系的数据.20世纪70年代,这种方法经过我国著名数学家华罗庚的倡导在我国得到大规模推广,取得了很大的成就
如图1的作法是由《几何原本》中给出:
(1)以线段为边作正方形.
(2)取的中点,连接.
(3)在的延长线上取点,使.
(4)以线段为边作正方形.
点就是线段的黄金分割点.
以下是证明点是线段的黄金分割点的部分过程.
证明:设正方形的边长为1,则.
∵点是的中点,∴.
在中,由勾股定理得:.
…
任务:
(1)请根据上面的操作步骤,将上述证明过程补充完整.
(2)如图2,点,是线段的两个黄金分割点,且,则_____,_____.
答案
一、单选题
B.B.C.B.A.A.C.B.B
二、填空题
10.
11.10
12.
13.
14.()cm
.
15.
16.﹣2
17.
18.或
19.4
20..
三、解答题
21.解:
(1)满足≈0.618的矩形是黄金矩形;
(2)由=k得,BP=1×k=k,从而AP=1﹣k,
由得,BP2=AP×AB,
即k2=(1﹣k)×1,
解得k=,
∵k>0,
∴k=≈0.618;
(3)因为点P是线段AB的黄金分割点,所以,
设△ABC的AB上的高为h,则
,
∴
∴直线CP是△ABC的黄金分割线.
(4)由(2)知,在BC边上也存在这样的黄金分割点Q,则AQ也是黄金分割线,设AQ与CP交于点W,则过点W的直线均是△ABC的黄金分割线,故黄金分割线有无数条.
22.解:∵,
又∵D是AB的黄金分割点,
∴,,
∴CD是△ABC的黄金分割线;
(2)不是.
∵CD是△ABC的中线,
∴AD=DB,
∴,
而,
∴,
∴中线不是黄金分割线.
23.(1)解:直线是的黄金分割线.理由如下:
设的边上的高为h.
则,,,
∴,.
又∵点D为边的黄金分割点,
∴,
∴.
故直线是的黄金分割线;
(2)解:∵三角形的中线将三角形分成面积相等的两部分,
∴,即
故三角形的中线不可能是该三角形的黄金分割线;
(3)解:∵,
∴和的公共边上的高也相等,
∴,
∴,
.
又∵,
∴.
因此,直线也是的黄金分割线;
(4)解:画法不唯一,现提供两种画法;
画法一:如解图①,取的中点G,再过点G作一条直线分别交,于M,N点,则直线就是平行四边形的黄金分割线.
画法二:如解图②,在上取一点N,连接,再过点F作交于点M,连接,则直线就是平行四边形的黄金分割线.
24.解:设,,则,
由,得,
则,
整理得;,
解得:,(不合题意,舍去).
故黄金比为:.
25.(1)证明:设正方形的边长为1,则.
∵点是的中点,
∴.
在中,由勾股定理得:,
则,
∴,
∴,,
即.
故点是线段的黄金分割点.
(2)解:∵点是的黄金分割点,
根据(1)可得,解得,
则.
故答案为4,.
一、单选题
1.生活中到处可见黄金分割的美.如图,点C将线段AB分成AC、CB两部分,且AC>BC,如果,那么称点C为线段AB的黄金分割点.若C是线段AB的黄金分割点,AB=2,则分割后较短线段长为( )
A. B. C. D.
2.世界上最有名的建筑物中几乎都包含“黄金分割”,如成都广播电视塔同样蕴含着“黄金分割”,如图,塔高AB为339米,观光区P为塔AB的黄金分割点(AP>PB),那么AP的高度大约为( )米.
A.200 B.210 C.300 D.130
3.点是线段的黄金分割点,且,则的长为( )
A. B.
C.或 D.或
4.已知点是线段的黄金分割点,,则的值为( )
A. B. C.0.618 D.
5.如图,线段AB=1,点P1是线段AB的黄金分割点(且AP1<BP1,即P1B2=AP1 AB),点P2是线段AP1的黄金分割点(AP2<P1P2),点P3是线段AP2的黄金分割点(AP3<P2P3),…,依此类推,则线段AP2017的长度是( )
A.()2017 B.()2017 C.()2017 D.(﹣2)1008
6.古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段分为两线段,,使得其中较长的一段是全长与较短的段的比例中项,即满足,后人把这个数称为“黄金分割”数,把点G称为线段的“黄金分割”点.如图,在中,已知,,若D,E是边的两个“黄金分割”点,则的面积为( )
A. B. C. D.
7.有以下命题:
①如果线段是线段,,的第四比例项,则有;
②如果点是线段的中点,那么是、的比例中项;
③如果点是线段的黄金分割点,且,那么是与的比例中项;
④如果点是线段的黄金分割点,,且,则.
其中正确的判断有( )
A.②④ B.①②③④ C.①③④ D.②③④
8.采用如下方法可以得到线段的黄金分割点:如图,设AB是已知线段,经过点B做BD⊥AB,使;连接DA,在DA上取DE=DB,在AB上截取AC=AE.点C即为线段AB的黄金分割点,若BD=2,则BC的长为( )
A. B. C. D.
9.古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是(,称为黄金分割比例),如图,著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是.若某人满足上述两个黄金分割比例,且腿长为,头顶至脖子下端的长度为,则其身高可能是( )
A. B. C. D.
二、填空题
10.大自然巧夺天工,一片小小树叶,也蕴含着“黄金分割”.如图,为的黄金分割点,如果的长度为,那么的长度是______.
11.人们把这个数叫做黄金分割数,著名数学家华罗庚优选法中的法就应用了黄金分割数.设,,则,记,,…,.则____.
12.点是线段的黄金分割点,,若,则__.
13.如图,线段AB=1,点P1是线段AB的黄金分割点(AP1
15.已知线段,点c是线段的黄金分割点,.那么________.
16.“黄金分割”被视为最美丽的几何学比率,在建筑、艺术和日常生活中处处可见.如图,D、E是△ABC中边BC的两个“黄金分割”点,则△ADE与△ABC的面积之比是_____.
17.若线段,是的黄金分割点,且,则AC=
18.已知点为线段的黄金分割点,且,则线段的长为________.
19.点 C 是线段 AB 的黄金分割点(AC>BC),若 AC=2则 =______.
20.如图,正五边形ABCDE的各条对角线的交点为M,N,P,Q,R,它们分别是各条对角线的黄金分割点.若AB=2,则MN的长为__.
三、解答题
21.(如图1),点P将线段AB分成一条较小线段AP和一条较大线段BP,如果,那么称点P为线段AB的黄金分割点,设=k,则k就是黄金比,并且k≈0.618.
(1)以图1中的AP为底,BP为腰得到等腰△APB(如图2),等腰△APB即为黄金三角形,黄金三角形的定义为:满足≈0.618的等腰三角形是黄金三角形;类似地,请你给出黄金矩形的定义: ;
(2)如图1,设AB=1,请你说明为什么k约为0.618;
(3)由线段的黄金分割点联想到图形的“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成面积为S1和面积为S2的两部分(设S1<S2),如果,那么称直线l为该矩形的黄金分割线.(如图3),点P是线段AB的黄金分割点,那么直线CP是△ABC的黄金分割线吗?请说明理由;
(4)图3中的△ABC的黄金分割线有几条?
22.如图1所示,点C将线段AB分成两部分,如果,那么点C为线段AB的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2,如果,那么称直线l为该图形的黄金分割线.
(1)研究小组猜想:在△ABC中,若点D为AB边上的黄金分割点,如图2所示,则直线CD是△ABC的黄金分割线,你认为对吗?说说你的理由;
(2)请你说明:三角形的中线是否是该三角形的黄金分割线.
23.如图①,点C将线段分成两部分,如果,那么称点C为线段的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为,,如果,那么称直线l为该图形的黄金分割线.
(1)研究小组猜想:在中,若点D为边上的黄金分割点(如图②),则直线是的黄金分割线.你认为对吗?为什么?
(2)请你说明:三角形的中线是否也是该三角形的黄金分割线?
(3)在(1)中的中,研究小组在进一步探究中发现:过点C任作一条直线交于点E,再过点D作直线,交AC于点F,连接(如图③),则直线也是的黄金分割线.请你说明理由;
(4)如图④,点E是平行四边形的边的黄金分割点,过点E作,交于点F,显然直线是平行四边形的黄金分割线.请你画一条平行四边形的黄金分割线,使它不经过平行四边形各边黄金分割点.
24.一般地,点把线段分成两条线段和,如果,那么称线段被点黄金分割,点叫做线段的黄金分割点,与的比叫做黄金比.请计算黄金比.
25.阅读与思考
黄金分割
黄金分割起源于古希腊的毕达哥拉斯学派,公元前4世纪,古希腊数学家欧多克索斯第一个系统研究了黄金分割比例这一问题,并建立起比例理论.后来欧几里得进一步系统论述了黄金分割,其《几何原本》成为最早的有关黄金分割的论著.黄金分割指的是把一条线段分成两部分,使其中较长部分与线段总长之比等于较短部分与较长部分之比.
黄金分割在美学、艺术、建筑和日常生活方面有看广泛的应用.如埃及的金字塔、印度的泰姬陵等,都可发现与黄金比有联系的数据.20世纪70年代,这种方法经过我国著名数学家华罗庚的倡导在我国得到大规模推广,取得了很大的成就
如图1的作法是由《几何原本》中给出:
(1)以线段为边作正方形.
(2)取的中点,连接.
(3)在的延长线上取点,使.
(4)以线段为边作正方形.
点就是线段的黄金分割点.
以下是证明点是线段的黄金分割点的部分过程.
证明:设正方形的边长为1,则.
∵点是的中点,∴.
在中,由勾股定理得:.
…
任务:
(1)请根据上面的操作步骤,将上述证明过程补充完整.
(2)如图2,点,是线段的两个黄金分割点,且,则_____,_____.
答案
一、单选题
B.B.C.B.A.A.C.B.B
二、填空题
10.
11.10
12.
13.
14.()cm
.
15.
16.﹣2
17.
18.或
19.4
20..
三、解答题
21.解:
(1)满足≈0.618的矩形是黄金矩形;
(2)由=k得,BP=1×k=k,从而AP=1﹣k,
由得,BP2=AP×AB,
即k2=(1﹣k)×1,
解得k=,
∵k>0,
∴k=≈0.618;
(3)因为点P是线段AB的黄金分割点,所以,
设△ABC的AB上的高为h,则
,
∴
∴直线CP是△ABC的黄金分割线.
(4)由(2)知,在BC边上也存在这样的黄金分割点Q,则AQ也是黄金分割线,设AQ与CP交于点W,则过点W的直线均是△ABC的黄金分割线,故黄金分割线有无数条.
22.解:∵,
又∵D是AB的黄金分割点,
∴,,
∴CD是△ABC的黄金分割线;
(2)不是.
∵CD是△ABC的中线,
∴AD=DB,
∴,
而,
∴,
∴中线不是黄金分割线.
23.(1)解:直线是的黄金分割线.理由如下:
设的边上的高为h.
则,,,
∴,.
又∵点D为边的黄金分割点,
∴,
∴.
故直线是的黄金分割线;
(2)解:∵三角形的中线将三角形分成面积相等的两部分,
∴,即
故三角形的中线不可能是该三角形的黄金分割线;
(3)解:∵,
∴和的公共边上的高也相等,
∴,
∴,
.
又∵,
∴.
因此,直线也是的黄金分割线;
(4)解:画法不唯一,现提供两种画法;
画法一:如解图①,取的中点G,再过点G作一条直线分别交,于M,N点,则直线就是平行四边形的黄金分割线.
画法二:如解图②,在上取一点N,连接,再过点F作交于点M,连接,则直线就是平行四边形的黄金分割线.
24.解:设,,则,
由,得,
则,
整理得;,
解得:,(不合题意,舍去).
故黄金比为:.
25.(1)证明:设正方形的边长为1,则.
∵点是的中点,
∴.
在中,由勾股定理得:,
则,
∴,
∴,,
即.
故点是线段的黄金分割点.
(2)解:∵点是的黄金分割点,
根据(1)可得,解得,
则.
故答案为4,.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
