2.3简单的轴对称图形 学案 鲁教版(五四制)数学七年级上册
文档属性
| 名称 | 2.3简单的轴对称图形 学案 鲁教版(五四制)数学七年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 165.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-09 13:57:03 | ||
图片预览


文档简介
2.3简单的轴对称图形
课时一:
【学习目标】
1.探索并掌握线段的垂直平分线的性质; 2.掌握线段的垂直平分线的尺规作图;
3.在“操作--探究---归纳---说理”过程中学会有条理地思考和表达,提高演绎推理能力.
【课前预习】阅读课本第46至47页的内容,思考并解答下列问题.
1.按照下面的步骤做一做.
(1)画一条线段AB,对折AB使点A、B重合,折痕与AB的交点为O. (2)在折痕上任取一点C,沿CA将纸折叠. (3)把纸展开,得到折痕CA和CB.
(1)线段是轴对称图形吗?如果是,它的对称轴是什么?
(2)CO与AB有怎样的位置关系?
(3)OA与OB相等吗?CA与CB呢?能说明你的理由吗?
在折痕上另取一点,再试一试.
归纳:1.线段是________图形,线段的__________是它的对称轴;
2.线段的垂直平分线上的点到________________相等.
思考:一条线段有_________条对称轴.
3.如图,直线 l上一点Q满足QA=QB,则Q点是直线l与_________的交点.画图说明.
【课中实施】
点拨:如果直线MN是线段AB的垂直平分线,那么给出一点O,不管O点是在直线上,还是在直线外,只要O点在MN上,我们就可以得出结论:OA=OB.反之亦成立.
【当堂达标】(共10分)
1.线段垂直平分线上的点到这条线段两个端点的距离__________.(1分)
2.到三角形的三个顶点距离相等的点是 ( )(1分)
A.三条角平分线的交点 B.三条中线的交点
C.三条高的交点 D.三条边的垂直平分线的交点
3.在Rt△ABC中,∠C=90°,AC>BC,AB的垂直平分线与AC相交于E点,连结BE,若∠CBE∶∠EBA=1∶4,则∠A=______度,∠ABC=_________度.(1分)
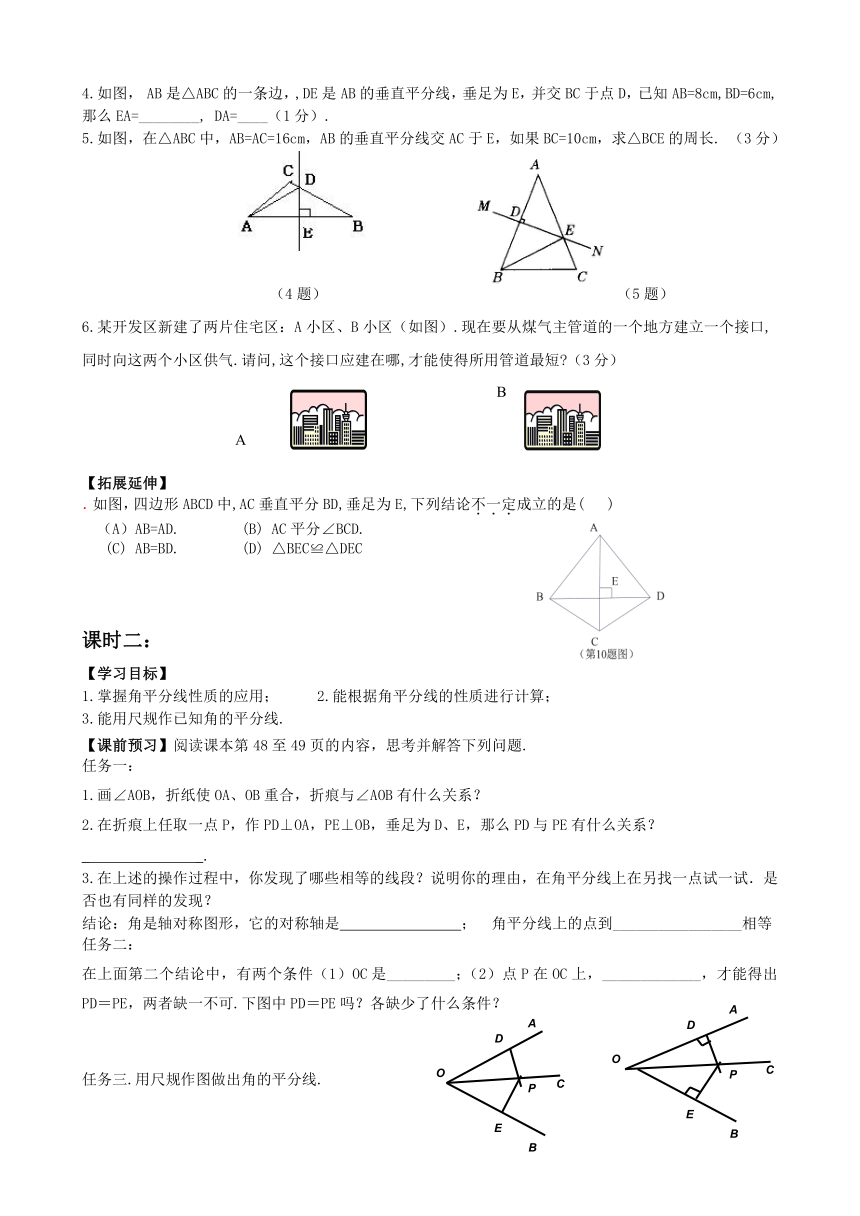
4.如图, AB是△ABC的一条边,,DE是AB的垂直平分线,垂足为E,并交BC于点D,已知AB=8cm,BD=6cm,那么EA=________, DA=____(1分).
5.如图,在△ABC中,AB=AC=16cm,AB的垂直平分线交AC于E,如果BC=10cm,求△BCE的周长. (3分)
(4题) (5题)
6.某开发区新建了两片住宅区:A小区、B小区(如图).现在要从煤气主管道的一个地方建立一个接口,同时向这两个小区供气.请问,这个接口应建在哪,才能使得所用管道最短 (3分)
【拓展延伸】
.如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )
(A)AB=AD. (B) AC平分∠BCD.
(C) AB=BD. (D) △BEC≌△DEC
课时二:
【学习目标】
1.掌握角平分线性质的应用; 2.能根据角平分线的性质进行计算;
3.能用尺规作已知角的平分线.
【课前预习】阅读课本第48至49页的内容,思考并解答下列问题.
任务一:
1.画∠AOB,折纸使OA、OB重合,折痕与∠AOB有什么关系?
2.在折痕上任取一点P,作PD⊥OA,PE⊥OB,垂足为D、E,那么PD与PE有什么关系?
_ _.
3.在上述的操作过程中,你发现了哪些相等的线段?说明你的理由,在角平分线上在另找一点试一试.是否也有同样的发现?
结论:角是轴对称图形,它的对称轴是 ; 角平分线上的点到_________________相等
任务二:
在上面第二个结论中,有两个条件(1)OC是_________;(2)点P在OC上,_____________,才能得出PD=PE,两者缺一不可.下图中PD=PE吗?各缺少了什么条件?
任务三.用尺规作图做出角的平分线.
【当堂达标】(共10分)
1.角的平分线上的点到这个角的两边的距离__________.(1分)
2.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,
则下列说法中正确的个数是( )(1分)
①AD是∠BAC的平分线;②∠ADC=60°;
③AD=AB; ④∠ADB=120°.
A.1 B.2 C.3 D.4.
3.如图,OC是∠AOB的平分线,点P在OC上,PO⊥OA,PE⊥OB,垂足分别是D、E,PE=2.5cm,则PD=__________cm.(2分)
4.如图,已知∠C=90°,∠1=∠2,若BC=10,BD=6,则点D到边AB的距离为_____.
(2分)
5.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D. 若BD:DC=3:2,点D到AB的距离为6,则BC的长是 . (2分)
6.某地有两所大学和两条相交叉的公路,如图所示(点C,D表示大学,AO,BO表示公路).现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.(2分)
(1)你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案;
(2)阐述你设计的理由.
课时三:
【学习目标】
1.掌握等腰三角形、等边三角形性质的应用; 2.理解等腰三角形的性质并会用符号语言表示;
3.认识等边三角形的轴对称性及性质.
【课前预习】
阅读课本第50至51页的内容,思考并解答下列问题.
任务一:拿出你准备的等腰三角形纸片,记作△ABC.把纸片折折看,让两腰AB、AC重叠在一起,折痕为AD.你能发现什么现象吗?
(1)等腰三角形___轴对称图形。(是或不是)
(2)∠B = ___ (3 )∠BAD=___ , AD为顶角的___.
(4)∠ADB=∠ADC=90°,AD为底边上的___.
(5 )BD= ___ ,AD为底边上的 .
结论:等腰三角形的两个_______相等
等腰三角形的 平分线、 上的高和 上的中线互相重合(简称“三线合一”)
几何语言: 在△ABC中, AB=AC时,
(1)若AD平分∠BAC,那么 、
(2)若BD=CD,那么 、
(3)若AD⊥BC,那么 、
任务二:如图,在△ABC中,若AB=AC=BC,则∠B=∠C=∠A
思考(1)等边三角形有几条对称轴?
(2)你能发现等边三角那些特征?
结论: 1.等边三角形是______________,并且有____条对称轴.
2.等边三角形的每个内角都等于________.
【当堂达标】(共10分)
1.等腰三角形是轴对称图形,它的对称轴是( )(1分)
A.过顶点的直线 B.顶角平分线所在的直线
C.底边上的中线 D. 底边上的高
2.等腰三角形的一个角是80°,则它的底角是 ( )(1分)
A.50° B.80° C.20°或80° D.50°或80°
3.等腰三角形中,若底角是65°,则顶角的度数是_____;
等腰三角形的周长为10cm,一边长为3cm,则其他两边长分别为_____;
等腰三角形一个角为70°,则其他两个角分别是_____ . (3分)
4.一个等腰三角形的顶角是底角的两倍,求它的各个内角的度数。(2分)
5.如图,AB = AC = AD,且AD∥BC,
∠C =2∠D吗?试说明理由.(3分)
【拓展延伸】
已知:如图,ΔABC中,AB=AC,D、E在BC边上,且AD=AE.试说明BD=CE.
课时四:
【学习目标】
1.掌握等腰三角形和等边三角形的判定方法; 2.认识和探索30°直角三角形的性质;
3.会综合运用等腰三角形的性质和判定进行有关的计算和推理.
【课前预习】
阅读课本第52至53页的内容,思考并解答下列问题.
(1)预习作业:等腰三角形的判定方法?
定义:有 相等的三角形,叫做等腰三角形.
判定: .
试说明理由:
(2)等边三角形的判定方法?
定义:有 相等的三角形,叫做等边三角形.
判定方法1:三个角都相等的三角形是 三角形;
判定方法2:有一个角等于600 的等腰三角形是 三角形.
应用:在直角三角形中,如果一个锐角 ,那么 的一半.
(3)如图,∠CAE是△ABC的外角,∠1=∠2,AD∥BC
试说明:AB=AC
【当堂达标】(共10分)
1.把两个都有一个锐角为30°的一样大小的直角三角形拼成如图所示的图形,两条直角边在同一直线上,则图中等腰三角形的个数是( )(2分)
A.1个 B.2个 C.3个 D.4个
2.下列两个图形是否是等腰三角形? (2分)
3.如图,∠A=∠B,CE∥DA,CE交AB于E,试说明△CEB是等腰三角形(3分)
4.如图:已知△ABC中,AB=AC, ∠C=30°,AB⊥AD,AD=2cm,求BC的长(3分)
【拓展延伸】
已知AB=AC,D是AB上一点,DE⊥BC于E,ED的延长线交CA的延长线于F,试说明
△ADF是等腰三角形的理由.
课时一:
【学习目标】
1.探索并掌握线段的垂直平分线的性质; 2.掌握线段的垂直平分线的尺规作图;
3.在“操作--探究---归纳---说理”过程中学会有条理地思考和表达,提高演绎推理能力.
【课前预习】阅读课本第46至47页的内容,思考并解答下列问题.
1.按照下面的步骤做一做.
(1)画一条线段AB,对折AB使点A、B重合,折痕与AB的交点为O. (2)在折痕上任取一点C,沿CA将纸折叠. (3)把纸展开,得到折痕CA和CB.
(1)线段是轴对称图形吗?如果是,它的对称轴是什么?
(2)CO与AB有怎样的位置关系?
(3)OA与OB相等吗?CA与CB呢?能说明你的理由吗?
在折痕上另取一点,再试一试.
归纳:1.线段是________图形,线段的__________是它的对称轴;
2.线段的垂直平分线上的点到________________相等.
思考:一条线段有_________条对称轴.
3.如图,直线 l上一点Q满足QA=QB,则Q点是直线l与_________的交点.画图说明.
【课中实施】
点拨:如果直线MN是线段AB的垂直平分线,那么给出一点O,不管O点是在直线上,还是在直线外,只要O点在MN上,我们就可以得出结论:OA=OB.反之亦成立.
【当堂达标】(共10分)
1.线段垂直平分线上的点到这条线段两个端点的距离__________.(1分)
2.到三角形的三个顶点距离相等的点是 ( )(1分)
A.三条角平分线的交点 B.三条中线的交点
C.三条高的交点 D.三条边的垂直平分线的交点
3.在Rt△ABC中,∠C=90°,AC>BC,AB的垂直平分线与AC相交于E点,连结BE,若∠CBE∶∠EBA=1∶4,则∠A=______度,∠ABC=_________度.(1分)
4.如图, AB是△ABC的一条边,,DE是AB的垂直平分线,垂足为E,并交BC于点D,已知AB=8cm,BD=6cm,那么EA=________, DA=____(1分).
5.如图,在△ABC中,AB=AC=16cm,AB的垂直平分线交AC于E,如果BC=10cm,求△BCE的周长. (3分)
(4题) (5题)
6.某开发区新建了两片住宅区:A小区、B小区(如图).现在要从煤气主管道的一个地方建立一个接口,同时向这两个小区供气.请问,这个接口应建在哪,才能使得所用管道最短 (3分)
【拓展延伸】
.如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )
(A)AB=AD. (B) AC平分∠BCD.
(C) AB=BD. (D) △BEC≌△DEC
课时二:
【学习目标】
1.掌握角平分线性质的应用; 2.能根据角平分线的性质进行计算;
3.能用尺规作已知角的平分线.
【课前预习】阅读课本第48至49页的内容,思考并解答下列问题.
任务一:
1.画∠AOB,折纸使OA、OB重合,折痕与∠AOB有什么关系?
2.在折痕上任取一点P,作PD⊥OA,PE⊥OB,垂足为D、E,那么PD与PE有什么关系?
_ _.
3.在上述的操作过程中,你发现了哪些相等的线段?说明你的理由,在角平分线上在另找一点试一试.是否也有同样的发现?
结论:角是轴对称图形,它的对称轴是 ; 角平分线上的点到_________________相等
任务二:
在上面第二个结论中,有两个条件(1)OC是_________;(2)点P在OC上,_____________,才能得出PD=PE,两者缺一不可.下图中PD=PE吗?各缺少了什么条件?
任务三.用尺规作图做出角的平分线.
【当堂达标】(共10分)
1.角的平分线上的点到这个角的两边的距离__________.(1分)
2.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,
则下列说法中正确的个数是( )(1分)
①AD是∠BAC的平分线;②∠ADC=60°;
③AD=AB; ④∠ADB=120°.
A.1 B.2 C.3 D.4.
3.如图,OC是∠AOB的平分线,点P在OC上,PO⊥OA,PE⊥OB,垂足分别是D、E,PE=2.5cm,则PD=__________cm.(2分)
4.如图,已知∠C=90°,∠1=∠2,若BC=10,BD=6,则点D到边AB的距离为_____.
(2分)
5.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D. 若BD:DC=3:2,点D到AB的距离为6,则BC的长是 . (2分)
6.某地有两所大学和两条相交叉的公路,如图所示(点C,D表示大学,AO,BO表示公路).现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.(2分)
(1)你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案;
(2)阐述你设计的理由.
课时三:
【学习目标】
1.掌握等腰三角形、等边三角形性质的应用; 2.理解等腰三角形的性质并会用符号语言表示;
3.认识等边三角形的轴对称性及性质.
【课前预习】
阅读课本第50至51页的内容,思考并解答下列问题.
任务一:拿出你准备的等腰三角形纸片,记作△ABC.把纸片折折看,让两腰AB、AC重叠在一起,折痕为AD.你能发现什么现象吗?
(1)等腰三角形___轴对称图形。(是或不是)
(2)∠B = ___ (3 )∠BAD=___ , AD为顶角的___.
(4)∠ADB=∠ADC=90°,AD为底边上的___.
(5 )BD= ___ ,AD为底边上的 .
结论:等腰三角形的两个_______相等
等腰三角形的 平分线、 上的高和 上的中线互相重合(简称“三线合一”)
几何语言: 在△ABC中, AB=AC时,
(1)若AD平分∠BAC,那么 、
(2)若BD=CD,那么 、
(3)若AD⊥BC,那么 、
任务二:如图,在△ABC中,若AB=AC=BC,则∠B=∠C=∠A
思考(1)等边三角形有几条对称轴?
(2)你能发现等边三角那些特征?
结论: 1.等边三角形是______________,并且有____条对称轴.
2.等边三角形的每个内角都等于________.
【当堂达标】(共10分)
1.等腰三角形是轴对称图形,它的对称轴是( )(1分)
A.过顶点的直线 B.顶角平分线所在的直线
C.底边上的中线 D. 底边上的高
2.等腰三角形的一个角是80°,则它的底角是 ( )(1分)
A.50° B.80° C.20°或80° D.50°或80°
3.等腰三角形中,若底角是65°,则顶角的度数是_____;
等腰三角形的周长为10cm,一边长为3cm,则其他两边长分别为_____;
等腰三角形一个角为70°,则其他两个角分别是_____ . (3分)
4.一个等腰三角形的顶角是底角的两倍,求它的各个内角的度数。(2分)
5.如图,AB = AC = AD,且AD∥BC,
∠C =2∠D吗?试说明理由.(3分)
【拓展延伸】
已知:如图,ΔABC中,AB=AC,D、E在BC边上,且AD=AE.试说明BD=CE.
课时四:
【学习目标】
1.掌握等腰三角形和等边三角形的判定方法; 2.认识和探索30°直角三角形的性质;
3.会综合运用等腰三角形的性质和判定进行有关的计算和推理.
【课前预习】
阅读课本第52至53页的内容,思考并解答下列问题.
(1)预习作业:等腰三角形的判定方法?
定义:有 相等的三角形,叫做等腰三角形.
判定: .
试说明理由:
(2)等边三角形的判定方法?
定义:有 相等的三角形,叫做等边三角形.
判定方法1:三个角都相等的三角形是 三角形;
判定方法2:有一个角等于600 的等腰三角形是 三角形.
应用:在直角三角形中,如果一个锐角 ,那么 的一半.
(3)如图,∠CAE是△ABC的外角,∠1=∠2,AD∥BC
试说明:AB=AC
【当堂达标】(共10分)
1.把两个都有一个锐角为30°的一样大小的直角三角形拼成如图所示的图形,两条直角边在同一直线上,则图中等腰三角形的个数是( )(2分)
A.1个 B.2个 C.3个 D.4个
2.下列两个图形是否是等腰三角形? (2分)
3.如图,∠A=∠B,CE∥DA,CE交AB于E,试说明△CEB是等腰三角形(3分)
4.如图:已知△ABC中,AB=AC, ∠C=30°,AB⊥AD,AD=2cm,求BC的长(3分)
【拓展延伸】
已知AB=AC,D是AB上一点,DE⊥BC于E,ED的延长线交CA的延长线于F,试说明
△ADF是等腰三角形的理由.
