5.3.1 平行线的性质——平行线间的拐点问题 课件(共43张PPT) 2022—2023学年人教版数学七年级下册
文档属性
| 名称 | 5.3.1 平行线的性质——平行线间的拐点问题 课件(共43张PPT) 2022—2023学年人教版数学七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 615.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-09 00:00:00 | ||
图片预览





文档简介
(共43张PPT)
平 行 线 间 的 拐 点 问 题
课堂目标
1、根据关键特征识别子弹图、猪手图模型,能独立推导并掌握模型结论;
2、掌握作辅助线方法及规范的几何语言;
3、能灵活运用“子弹图、猪手图”模型解决延伸问题。
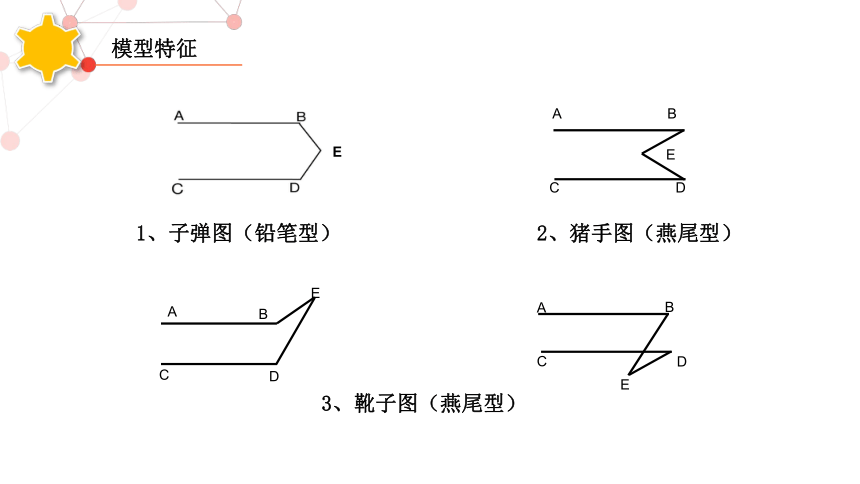
1、子弹图(铅笔型)
2、猪手图(燕尾型)
A
B
C
D
E
E
A
B
C
D
E
A
B
C
D
E
3、靴子图(燕尾型)
模型特征
A
B
C
D
E
E
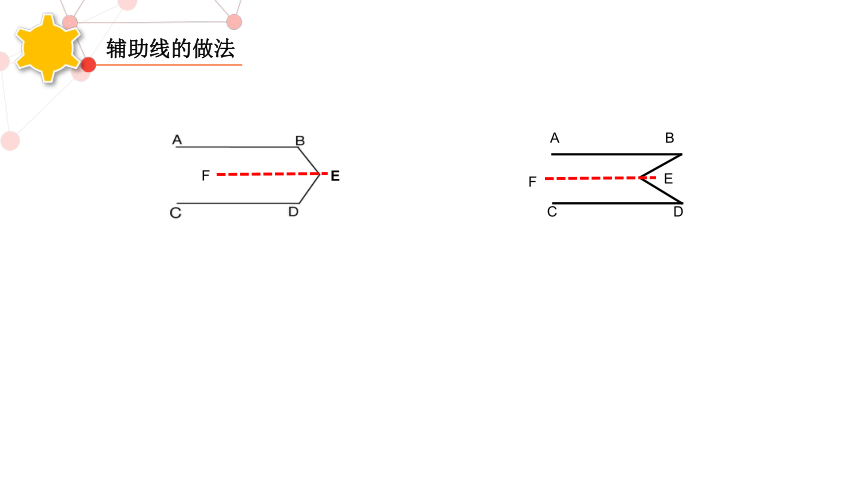
辅助线的做法
F
F
A
B
C
D
E
E
辅助线的做法
F
F
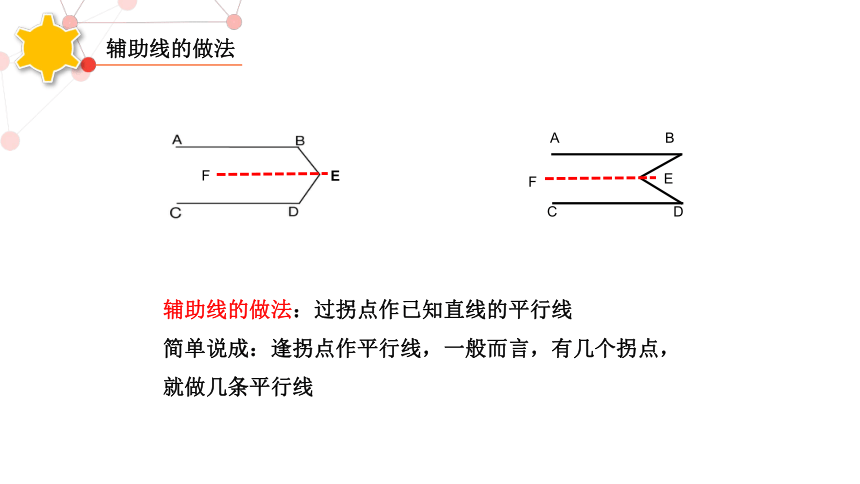
辅助线的做法:过拐点作已知直线的平行线
简单说成:逢拐点作平行线,一般而言,有几个拐点,就做几条平行线
辅助线的做法:过拐点作已知直线的平行线
简单说成:逢拐点作平行线,一般而言,有几个拐点,就做几条平行线
核心方法
1、子弹图
A
B
C
D
A
B
C
D
E
E
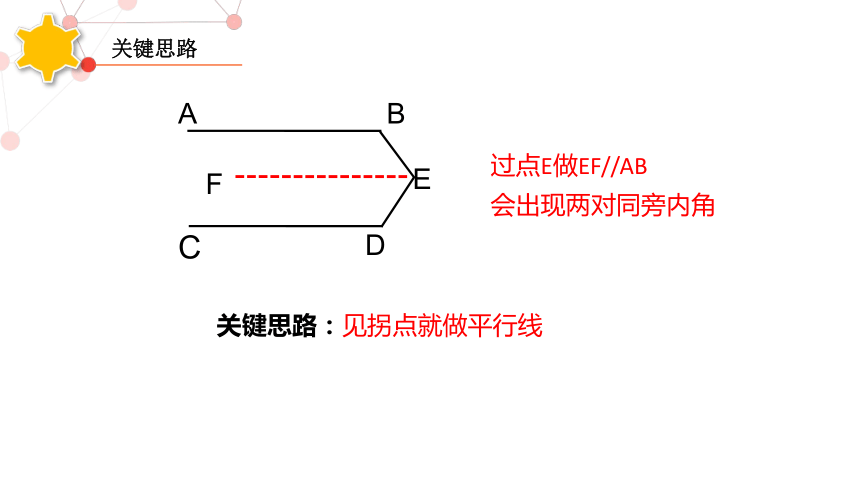
关键思路
A
B
E
C
D
F
关键思路:见拐点就做平行线
过点E做EF//AB
会出现两对同旁内角
关键结论
A
B
C
D
E
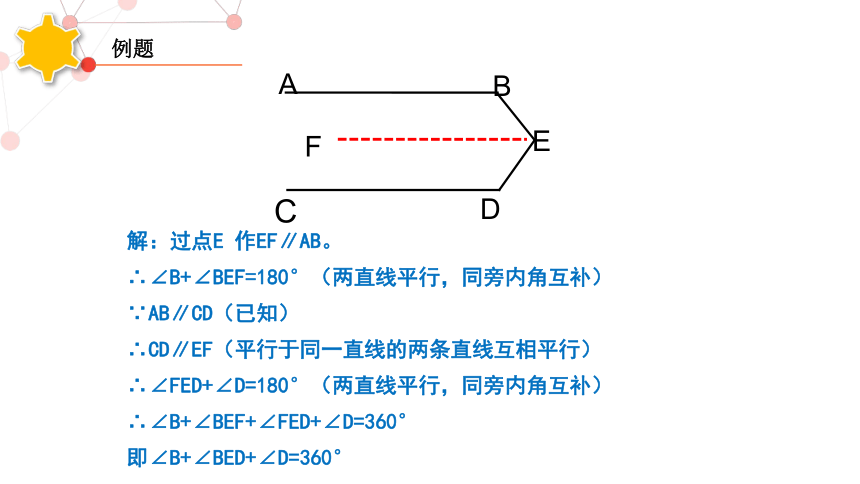
例题
如图1,已知:AB∥CD,点E是平面内一点,那么∠BED与∠B、∠D之间的数量关系是什么呢?
A
B
C
D
E
例题
解:过点E 作EF∥AB。
∴∠B+∠BEF=180°(两直线平行,同旁内角互补)
∵AB∥CD(已知)
∴CD∥EF(平行于同一直线的两条直线互相平行)
∴∠FED+∠D=180°(两直线平行,同旁内角互补)
∴∠B+∠BEF+∠FED+∠D=360°
即∠B+∠BED+∠D=360°
A
B
E
C
D
F
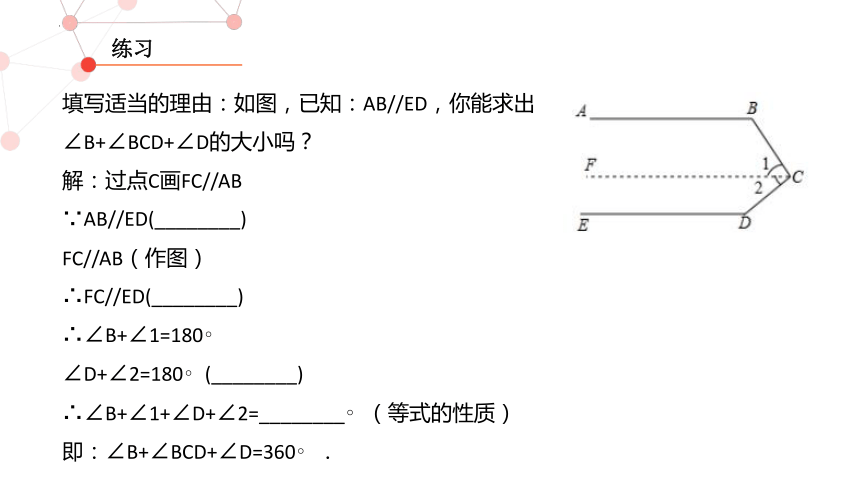
练习
填写适当的理由:如图,已知:AB//ED,你能求出∠B+∠BCD+∠D的大小吗?
解:过点C画FC//AB
∵AB//ED(________)
FC//AB(作图)
∴FC//ED(________)
∴∠B+∠1=180
∠D+∠2=180 (________)
∴∠B+∠1+∠D+∠2=________ (等式的性质)
即:∠B+∠BCD+∠D=360 .
已知,如图,AB//CD,若∠ABE=130 ,∠CDE=152 ,则∠BED=________.
练习
练习
如图,AB//CD,那么∠A+∠C+∠AEC=( )
A.360 B.270 C.200 D.180
A.40 B.50 C.60 D.70
如图,AB//DE,FG⊥BC于F,∠CDE=40 ,则∠FGB=( )
练习
如图,已知∠B+∠BCD+∠D=360 ,则AB//ED,为什么?
练习
解题思路:找拐点,作平行线
结论:平行线间每增加一个拐点,则角度和就增加一个180°即
∠1+∠2+∠3+.....+∠n=180+(n-2)*180=(n-1)*180(注:n为角的个数)
延伸
例题
(1)如图①,AB//CD,那么∠A+∠C=____度;
(2)如图②,AB//CD//EF,那么∠A+∠AEC+∠C=___度;
(3)如图③,AB//GH//MN//CD,那么 ∠A+∠AGM+∠GMC+∠C=______ _ 度,
并说明理由.
练习
如图,已知AB//CD,若按图中规律继续下去,则∠1+∠2+...+∠n=( )
A. n 180 B. 2n 180 C. (n 1) 180 D. (n 1)2 180
如图,直线AB//CD,则∠1+∠2+∠3+∠4+∠5+∠6=( )
练习
如图,AB//CD,则∠1+∠2+∠3+...+∠2n=________度.
练习
已知:如图,AB//CD,求:
(1)在图(1)中∠B+∠D=?
(2)在图(2)中∠B+∠E1+∠D=?
(3)在图(3)中∠B+∠E1+∠E2+...+∠En 1+∠En+∠D=?
练习
2、猪手图
E
E
A
B
C
D
A
B
C
D
关键思路
关键思路:见拐点就做平行线
过点E做EF//AB
会出现两对内错角
A
E
C
D
B
F
关键结论
A
B
C
D
E
例题
如图2,已知:AB∥CD,点E是平面内一点,那么∠BED与∠B、∠D之间的数量关系是什么呢?
A
B
C
D
图2
E
A
E
C
D
B
F
解:过点E 作EF∥AB。
∴∠B=∠BEF(两直线平行,内错角相等)
∵AB∥CD(已知)
∴EF∥CD(平行于同一直线的两条直线互相平行)
∴∠D=∠DEF(两直线平行,内错角相等)
∴∠B+∠D=∠BEF+∠DEF(等量代换)
∴∠B+∠D=∠BED
例题
完成正确的证明如图,已知AB//CD,求证:∠BED=∠B+∠D.
证明:过E点作EF//AB,
∴∠1=________.
∵AB//CD(已知),
∴EF//CD(________),
∴∠2=________.
又∠BED=∠1+∠2,
∴∠BED=∠B+∠D(________).
练习
如图所示,直线AB∥CD,∠B=23°,∠D=42°,则∠E= .
练习
练习
练习
练习
如图,AB//CD,∠BAE=120 ,∠DCE=30 ,则∠AEC=________度.
如图1是我们常用的折叠式小刀,图2中刀柄外形是一个矩形挖去一个小半圆,其中刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成如图2所示的∠1与∠2,则∠1与∠2的度数和是______度.
练习
练习
练习
如图,∠PCN=45°,直线CP与CN分别交AQ、EF于点B、D,∠ABC=20°,∠CDE=25°,试说明:AQ//EF.
如图,已知∠BED=∠B+∠D,试判断AB与CD的位置关系,并说明理由。(请用两种方法解答)
练习
延伸
即:∠1+∠3+∠5=∠2+∠4
开口朝左的所有角度之和与开口朝右的所有角度之和相等
例题
如图,AB//EF,∠C=90 ,则α,β,γ的关系为( )
A. β=α+γ B. α+β+γ=180 C. β+γ α=90 D. α+β γ=90
练习
如图,AB//EF,BC⊥CD,则∠α、∠β、∠γ之间的关系是( )
A.∠α ∠β+∠γ=90
B.∠α+∠β ∠γ=90
C.∠α ∠β+∠γ=180
D.∠β+∠γ ∠α=90
练习
如图,若直线l1//l2,∠α=∠β,∠1=40 ,则∠2的度数为_________.
练习
如图,AB//GF,试猜想∠B,∠C,∠D,∠E,∠F之间的关系,并证明.
练习
(1)如图甲,AB//CD,∠2与∠1+∠3的关系是什么?并写出推理过程;
(2)如图乙,AB//CD,直接写出∠2+∠4与∠1+∠3+∠5的数量关系;
(3)如图丙,AB//CD,试问∠2+∠4+∠6与∠1+∠3+∠5+∠7还有类似的数量关系吗?若有,请直接写出,并将它们推广到一般情况,用一句话写出你的结论.
总结
平行线的拐点问题
子弹图
猪手图
平 行 线 间 的 拐 点 问 题
课堂目标
1、根据关键特征识别子弹图、猪手图模型,能独立推导并掌握模型结论;
2、掌握作辅助线方法及规范的几何语言;
3、能灵活运用“子弹图、猪手图”模型解决延伸问题。
1、子弹图(铅笔型)
2、猪手图(燕尾型)
A
B
C
D
E
E
A
B
C
D
E
A
B
C
D
E
3、靴子图(燕尾型)
模型特征
A
B
C
D
E
E
辅助线的做法
F
F
A
B
C
D
E
E
辅助线的做法
F
F
辅助线的做法:过拐点作已知直线的平行线
简单说成:逢拐点作平行线,一般而言,有几个拐点,就做几条平行线
辅助线的做法:过拐点作已知直线的平行线
简单说成:逢拐点作平行线,一般而言,有几个拐点,就做几条平行线
核心方法
1、子弹图
A
B
C
D
A
B
C
D
E
E
关键思路
A
B
E
C
D
F
关键思路:见拐点就做平行线
过点E做EF//AB
会出现两对同旁内角
关键结论
A
B
C
D
E
例题
如图1,已知:AB∥CD,点E是平面内一点,那么∠BED与∠B、∠D之间的数量关系是什么呢?
A
B
C
D
E
例题
解:过点E 作EF∥AB。
∴∠B+∠BEF=180°(两直线平行,同旁内角互补)
∵AB∥CD(已知)
∴CD∥EF(平行于同一直线的两条直线互相平行)
∴∠FED+∠D=180°(两直线平行,同旁内角互补)
∴∠B+∠BEF+∠FED+∠D=360°
即∠B+∠BED+∠D=360°
A
B
E
C
D
F
练习
填写适当的理由:如图,已知:AB//ED,你能求出∠B+∠BCD+∠D的大小吗?
解:过点C画FC//AB
∵AB//ED(________)
FC//AB(作图)
∴FC//ED(________)
∴∠B+∠1=180
∠D+∠2=180 (________)
∴∠B+∠1+∠D+∠2=________ (等式的性质)
即:∠B+∠BCD+∠D=360 .
已知,如图,AB//CD,若∠ABE=130 ,∠CDE=152 ,则∠BED=________.
练习
练习
如图,AB//CD,那么∠A+∠C+∠AEC=( )
A.360 B.270 C.200 D.180
A.40 B.50 C.60 D.70
如图,AB//DE,FG⊥BC于F,∠CDE=40 ,则∠FGB=( )
练习
如图,已知∠B+∠BCD+∠D=360 ,则AB//ED,为什么?
练习
解题思路:找拐点,作平行线
结论:平行线间每增加一个拐点,则角度和就增加一个180°即
∠1+∠2+∠3+.....+∠n=180+(n-2)*180=(n-1)*180(注:n为角的个数)
延伸
例题
(1)如图①,AB//CD,那么∠A+∠C=____度;
(2)如图②,AB//CD//EF,那么∠A+∠AEC+∠C=___度;
(3)如图③,AB//GH//MN//CD,那么 ∠A+∠AGM+∠GMC+∠C=______ _ 度,
并说明理由.
练习
如图,已知AB//CD,若按图中规律继续下去,则∠1+∠2+...+∠n=( )
A. n 180 B. 2n 180 C. (n 1) 180 D. (n 1)2 180
如图,直线AB//CD,则∠1+∠2+∠3+∠4+∠5+∠6=( )
练习
如图,AB//CD,则∠1+∠2+∠3+...+∠2n=________度.
练习
已知:如图,AB//CD,求:
(1)在图(1)中∠B+∠D=?
(2)在图(2)中∠B+∠E1+∠D=?
(3)在图(3)中∠B+∠E1+∠E2+...+∠En 1+∠En+∠D=?
练习
2、猪手图
E
E
A
B
C
D
A
B
C
D
关键思路
关键思路:见拐点就做平行线
过点E做EF//AB
会出现两对内错角
A
E
C
D
B
F
关键结论
A
B
C
D
E
例题
如图2,已知:AB∥CD,点E是平面内一点,那么∠BED与∠B、∠D之间的数量关系是什么呢?
A
B
C
D
图2
E
A
E
C
D
B
F
解:过点E 作EF∥AB。
∴∠B=∠BEF(两直线平行,内错角相等)
∵AB∥CD(已知)
∴EF∥CD(平行于同一直线的两条直线互相平行)
∴∠D=∠DEF(两直线平行,内错角相等)
∴∠B+∠D=∠BEF+∠DEF(等量代换)
∴∠B+∠D=∠BED
例题
完成正确的证明如图,已知AB//CD,求证:∠BED=∠B+∠D.
证明:过E点作EF//AB,
∴∠1=________.
∵AB//CD(已知),
∴EF//CD(________),
∴∠2=________.
又∠BED=∠1+∠2,
∴∠BED=∠B+∠D(________).
练习
如图所示,直线AB∥CD,∠B=23°,∠D=42°,则∠E= .
练习
练习
练习
练习
如图,AB//CD,∠BAE=120 ,∠DCE=30 ,则∠AEC=________度.
如图1是我们常用的折叠式小刀,图2中刀柄外形是一个矩形挖去一个小半圆,其中刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成如图2所示的∠1与∠2,则∠1与∠2的度数和是______度.
练习
练习
练习
如图,∠PCN=45°,直线CP与CN分别交AQ、EF于点B、D,∠ABC=20°,∠CDE=25°,试说明:AQ//EF.
如图,已知∠BED=∠B+∠D,试判断AB与CD的位置关系,并说明理由。(请用两种方法解答)
练习
延伸
即:∠1+∠3+∠5=∠2+∠4
开口朝左的所有角度之和与开口朝右的所有角度之和相等
例题
如图,AB//EF,∠C=90 ,则α,β,γ的关系为( )
A. β=α+γ B. α+β+γ=180 C. β+γ α=90 D. α+β γ=90
练习
如图,AB//EF,BC⊥CD,则∠α、∠β、∠γ之间的关系是( )
A.∠α ∠β+∠γ=90
B.∠α+∠β ∠γ=90
C.∠α ∠β+∠γ=180
D.∠β+∠γ ∠α=90
练习
如图,若直线l1//l2,∠α=∠β,∠1=40 ,则∠2的度数为_________.
练习
如图,AB//GF,试猜想∠B,∠C,∠D,∠E,∠F之间的关系,并证明.
练习
(1)如图甲,AB//CD,∠2与∠1+∠3的关系是什么?并写出推理过程;
(2)如图乙,AB//CD,直接写出∠2+∠4与∠1+∠3+∠5的数量关系;
(3)如图丙,AB//CD,试问∠2+∠4+∠6与∠1+∠3+∠5+∠7还有类似的数量关系吗?若有,请直接写出,并将它们推广到一般情况,用一句话写出你的结论.
总结
平行线的拐点问题
子弹图
猪手图
