数学人教A版(2019)选择性必修第一册1.3.2空间向量运算的坐标表示课件(共33张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.3.2空间向量运算的坐标表示课件(共33张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-07 18:23:14 | ||
图片预览











文档简介
(共33张PPT)
第一章《空间向量与立体几何》人教A版2019选择性必修第一册1.3.2空间向量运算的坐标表示环节一:创设情境,引入课题
我们所在的教室即是一个三维立体图,如果以教室的一个墙角为始点,沿着三条墙缝作向量可以得到三个空间向量.
这三个空间向量是不共面的,那么如何用这三个向量表示空间中任意的向量呢?
平面向量运算的坐标表示 空间向量运算的坐标表示
问题1:有了空间向量的坐标表示,你能类比平面向量的坐标运算,得出空间向量运算的坐标表示并给出证明吗?
下面我们证明空间向量数量积运算的坐标表示.
其他运算的坐标表示可以类似证明,请同学们自己完成.
知识点1 空间向量及其运算的坐标表示
由上述结论可知,空间向量运算的坐标表示与平面向量运算的坐标表示是完全一致的.
例如,我们有:
一个空间向量的坐标等于表示此向量的有向线段的终点坐标减去起点坐标.
环节二:观察分析,感知概念
知识点2:空间向量共线或平行的判定
类似平面向量运算的坐标表示,我们还可以得到:
环节三:抽象概括,形成概念
知识点3.空间向量的模
知识点4.空间向量的夹角公式
环节四:辨析理解,深化概念
问题2:你能利用空间向量运算的坐标表示推导空间两点间的距离公式吗?
O
x
y
z
图1.3-7
这就是空间两点间的距离公式.
将空间向量的运算与向量的坐标表示结合起来,不仅可以解决夹角和距离的计算问题,而且可以使一些问题的解决变得简单.
P1
P2
知识点5.空间两点之间的距离公式
O
A
B
C
x
y
z
图1.3-8
D
A1
B1
C1
D1
F
E
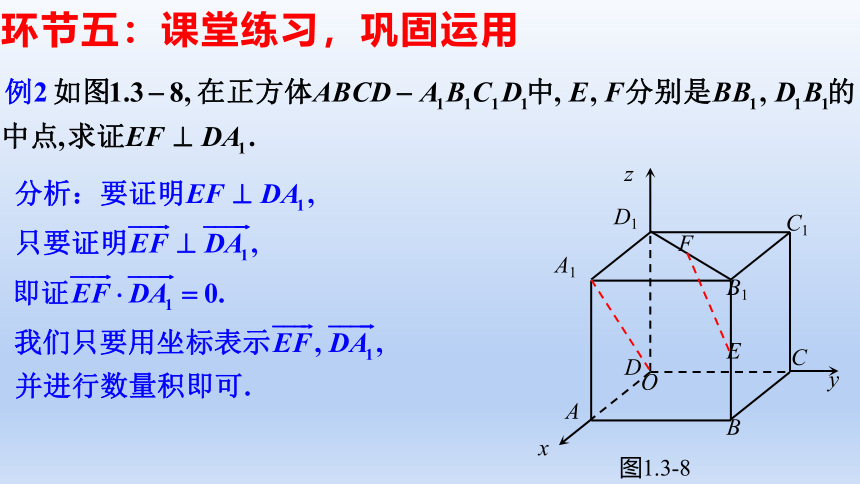
环节五:课堂练习,巩固运用
你能从本题的解答中体会到根据问题的特点,建立适当的空间直角坐标系,用向量表示相关元素,并通过向量及其坐标的运算求解问题的基本思路吗?
O
A
B
C
x
y
z
图1.3-8
D
A1
B1
C1
D1
F
E
O
A
B
C
x
y
z
图1.3-9
D
A1
B1
C1
D1
F1
M
E1
O
A
B
C
x
y
z
图1.3-9
D
A1
B1
C1
D1
F1
M
E1
环节六:归纳总结,反思提升
空间向量运算的坐标表示;
空间向量的长度公式与空间两点间的距离公式;
求两个向量的夹角或角的余弦值的关键是在合适的空间直角坐标系中找到两个向量的坐标,然后用公式计算.
1.基本知识:
环节六:归纳总结,反思提升
2. 思想方法
用向量计算或证明几何问题时,
可以先建立空间直角坐标系,
然后把向量点坐标化,
借助空间向量运算的坐标表示进行计算或证明.
环节七:目标检测,作业布置
教材第21-22页,
练习第1-5题,
习题1.3 第3-5题
练习(第21页)
环节七:目标检测,作业布置
O
A
B
C
x
y
z
M
N
O
A
B
C
x
y
z
M
N
A
B
C
(第5题)
D
A1
B1
C1
D1
M
z
y
x
习题 1.3(第22页)
“关于谁,谁不变,其余的相反”
O
A
B
C
x
y
z
(第3题)
H
I
J
E
F
G
作图略.
A
B
C
D
A1
B1
C1
D1
M
N
x
y
z
A
B
C
D
A1
B1
C1
D1
M
N
x
y
z
第一章《空间向量与立体几何》人教A版2019选择性必修第一册1.3.2空间向量运算的坐标表示环节一:创设情境,引入课题
我们所在的教室即是一个三维立体图,如果以教室的一个墙角为始点,沿着三条墙缝作向量可以得到三个空间向量.
这三个空间向量是不共面的,那么如何用这三个向量表示空间中任意的向量呢?
平面向量运算的坐标表示 空间向量运算的坐标表示
问题1:有了空间向量的坐标表示,你能类比平面向量的坐标运算,得出空间向量运算的坐标表示并给出证明吗?
下面我们证明空间向量数量积运算的坐标表示.
其他运算的坐标表示可以类似证明,请同学们自己完成.
知识点1 空间向量及其运算的坐标表示
由上述结论可知,空间向量运算的坐标表示与平面向量运算的坐标表示是完全一致的.
例如,我们有:
一个空间向量的坐标等于表示此向量的有向线段的终点坐标减去起点坐标.
环节二:观察分析,感知概念
知识点2:空间向量共线或平行的判定
类似平面向量运算的坐标表示,我们还可以得到:
环节三:抽象概括,形成概念
知识点3.空间向量的模
知识点4.空间向量的夹角公式
环节四:辨析理解,深化概念
问题2:你能利用空间向量运算的坐标表示推导空间两点间的距离公式吗?
O
x
y
z
图1.3-7
这就是空间两点间的距离公式.
将空间向量的运算与向量的坐标表示结合起来,不仅可以解决夹角和距离的计算问题,而且可以使一些问题的解决变得简单.
P1
P2
知识点5.空间两点之间的距离公式
O
A
B
C
x
y
z
图1.3-8
D
A1
B1
C1
D1
F
E
环节五:课堂练习,巩固运用
你能从本题的解答中体会到根据问题的特点,建立适当的空间直角坐标系,用向量表示相关元素,并通过向量及其坐标的运算求解问题的基本思路吗?
O
A
B
C
x
y
z
图1.3-8
D
A1
B1
C1
D1
F
E
O
A
B
C
x
y
z
图1.3-9
D
A1
B1
C1
D1
F1
M
E1
O
A
B
C
x
y
z
图1.3-9
D
A1
B1
C1
D1
F1
M
E1
环节六:归纳总结,反思提升
空间向量运算的坐标表示;
空间向量的长度公式与空间两点间的距离公式;
求两个向量的夹角或角的余弦值的关键是在合适的空间直角坐标系中找到两个向量的坐标,然后用公式计算.
1.基本知识:
环节六:归纳总结,反思提升
2. 思想方法
用向量计算或证明几何问题时,
可以先建立空间直角坐标系,
然后把向量点坐标化,
借助空间向量运算的坐标表示进行计算或证明.
环节七:目标检测,作业布置
教材第21-22页,
练习第1-5题,
习题1.3 第3-5题
练习(第21页)
环节七:目标检测,作业布置
O
A
B
C
x
y
z
M
N
O
A
B
C
x
y
z
M
N
A
B
C
(第5题)
D
A1
B1
C1
D1
M
z
y
x
习题 1.3(第22页)
“关于谁,谁不变,其余的相反”
O
A
B
C
x
y
z
(第3题)
H
I
J
E
F
G
作图略.
A
B
C
D
A1
B1
C1
D1
M
N
x
y
z
A
B
C
D
A1
B1
C1
D1
M
N
x
y
z
