数学人教A版(2019)必修第一册3.2.1函数的单调性(共28张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册3.2.1函数的单调性(共28张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-07 18:25:01 | ||
图片预览




文档简介
(共28张PPT)
第三章 函数的概念与性质
3.2.1 函数的单调性
高中数学/人教A版/必修一
知识篇
素养篇
思维篇
3.2.1 函数的单调性
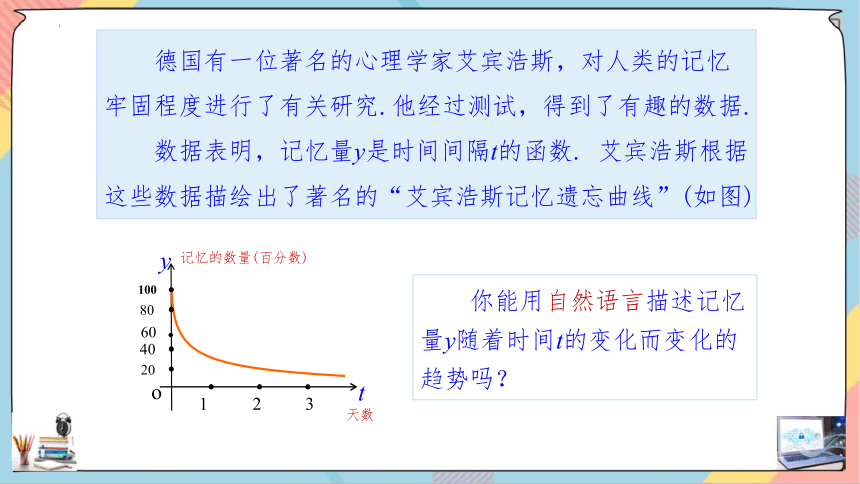
德国有一位著名的心理学家艾宾浩斯,对人类的记忆牢固程度进行了有关研究.他经过测试,得到了有趣的数据.
数据表明,记忆量y是时间间隔t的函数. 艾宾浩斯根据这些数据描绘出了著名的“艾宾浩斯记忆遗忘曲线”(如图)
1
2
3
t
y
o
20
40
60
80
记忆的数量(百分数)
天数
100
你能用自然语言描述记忆量y随着时间t的变化而变化的趋势吗?
在初中,我们利用函数图象研究过函数值随自变量的增大而增大(或减小)的性质,这一性质叫做函数的单调性.
下面进一步用符号语言刻画这种性质.
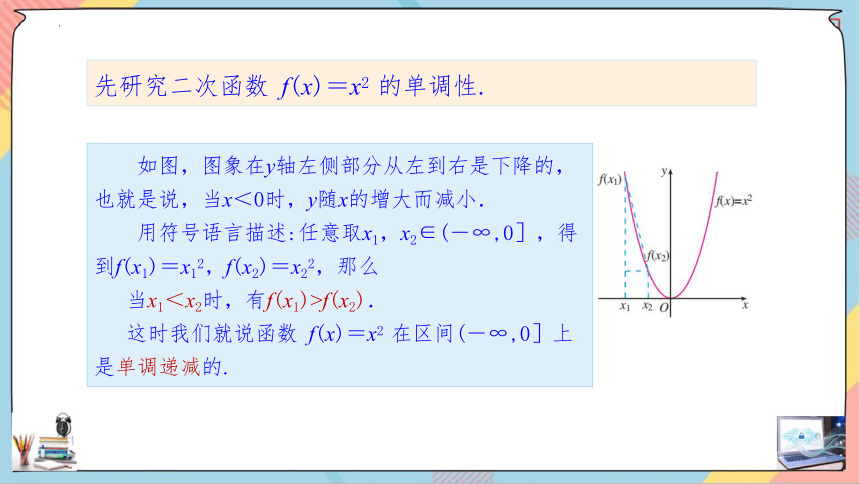
先研究二次函数 f(x)=x2 的单调性.
如图,图象在y轴左侧部分从左到右是下降的,也就是说,当x<0时,y随x的增大而减小.
用符号语言描述:任意取x1,x2∈(-∞,0],得到f(x1)=x12,f(x2)=x22,那么
当x1<x2时,有f(x1)>f(x2).
这时我们就说函数 f(x)=x2 在区间(-∞,0]上是单调递减的.
如图,图象在y轴右侧部分从左到右是上升的,也就是说,当x>0时,y随x的增大而增大.
用符号语言描述:任意取x1,x2∈[0,+∞),得到f(x1)=x12,f(x2)=x22,那么
当x1<x2时,有f(x1)< f(x2).
这时我们就说函数 f(x)=x2 在区间[0,+∞)上是单调递增的.
思考:
函数f(x)=-x2 和 f(x)=各有怎样的单调性?
1
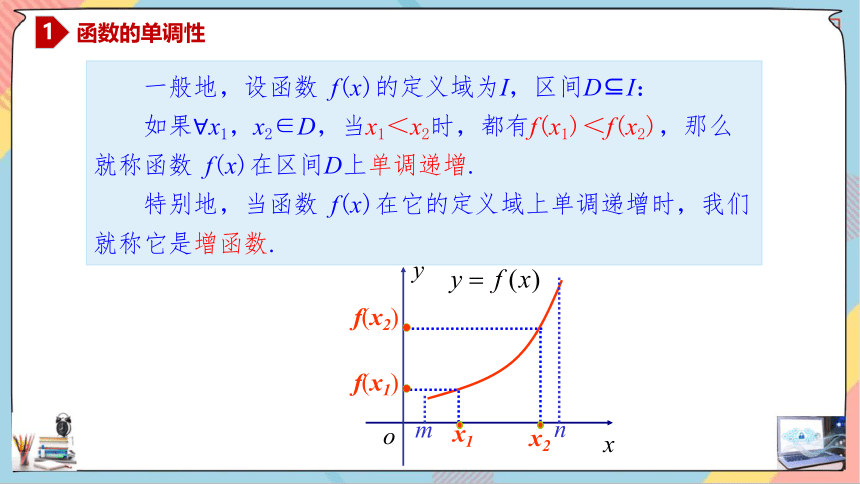
函数的单调性
一般地,设函数 f(x)的定义域为I,区间D I:
如果x1,x2∈D,当x1<x2时,都有f(x1)<f(x2),那么就称函数 f(x)在区间D上单调递增.
特别地,当函数 f(x)在它的定义域上单调递增时,我们就称它是增函数.
x
y
o
m
n
f(x1)
x1
x2
f(x2)
1
函数的单调性
一般地,设函数 f(x)的定义域为I,区间D I:
如果x1,x2∈D,当x1<x2时,都有f(x1)>f(x2),那么就称函数 f(x)在区间D上单调递减.
特别地,当函数 f(x)在它的定义域上单调递减时,我们就称它是减函数.
f(x1)
x1
x2
f(x2)
O
x
y
m
n
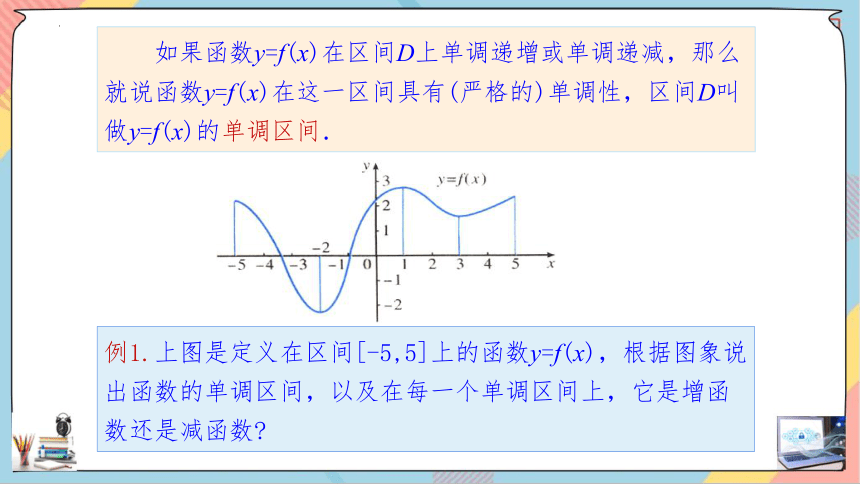
如果函数y=f(x)在区间D上单调递增或单调递减,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做y=f(x)的单调区间.
例1.上图是定义在区间[-5,5]上的函数y=f(x),根据图象说出函数的单调区间,以及在每一个单调区间上,它是增函数还是减函数
函数 f(x)= 有单调递减区间 ;
能否说 f(x)= 是单调递减函数?为什么?
思考
例2.根据定义证明以下各命题:
2
函数的单调性的证明
(1)函数f(x)= 在定义域上是增函数;
(2)函数 f(x)=-x3 在定义域上是减函数.
证明:(1)定义域为[0, + ∞).
x1,x2[0, + ∞),且x1y1-y2=
=
由x1所以,函数f(x)=在定义域上是增函数.
取点
作差
变形
定号
结论
例2.根据定义证明以下各命题:
2
函数的单调性的证明
(1)函数f(x)= 在定义域上是增函数;
(2)函数 f(x)=-x3 在定义域上是减函数
证明:(2)定义域为R.
x1,x2R,且x1y1-y2 = x23-x13 =(x2-x1)(x22-x1x2+x12)
=(x2-x1)[(x2-x1)2+x12]
由x10
得 y1-y2 > 0 ,即y1>y2
所以,函数f(x)=-x3 在定义域上是减函数.
根据定义证明函数 f(x)=x+ 在[1, +∞)上是增函数.
练一练
知识篇
素养篇
思维篇
3.2.1 函数的单调性
1)函数y=x2-4x+5的单调区间是 .
问题系列:
答案:单调递增区间:[2, +∞)
单调递减区间:[-∞, 2)
2)函数y=x2-4x+5在区间(4, 5)上单调递增吗?
问题系列:
答案:单调递增
3)函数y=x2-4x+5的单调递增区间是(4, 5)吗?
问题系列:
答案:不是
4)函数y=x2-4x+5在区间(k, 5)上单调,则k∈ ;
问题系列:
答案:2问题系列:
5)函数y=x2-4x+5在区间(k, k+3)上不单调,则
k∈ .
答案: -1知识篇
素养篇
思维篇
3.2.1 函数的单调性
1.若函数 的单调递减区间
为 ,则 a 的值为______.
答案:a=-3
2. 若函数 在区间
上是减函数,则实数 a 的取值范围是________.
答案:a≤-3
3. 若函数 f(x)是定义域为R的减函数,且 f(a-2)则a的取值范围是 ;
答案:4. 若函数 f(x)定义域为[-1, 1],对于x1,x2[-1, 1],
<0恒成立,且f(a-2)范围是 .
答案:课堂小结
一、本节课学习的新知识
函数的单调性
单调区间
二、本节课提升的核心素养
数学抽象
数据分析
课堂小结
直观想象
数学建模
三、本节课训练的数学思想方法
分类讨论
课堂小结
数形结合
函数思想
01
基础作业: .
02
能力作业: .
03
拓展延伸:(选做)
作业
第三章 函数的概念与性质
3.2.1 函数的单调性
高中数学/人教A版/必修一
知识篇
素养篇
思维篇
3.2.1 函数的单调性
德国有一位著名的心理学家艾宾浩斯,对人类的记忆牢固程度进行了有关研究.他经过测试,得到了有趣的数据.
数据表明,记忆量y是时间间隔t的函数. 艾宾浩斯根据这些数据描绘出了著名的“艾宾浩斯记忆遗忘曲线”(如图)
1
2
3
t
y
o
20
40
60
80
记忆的数量(百分数)
天数
100
你能用自然语言描述记忆量y随着时间t的变化而变化的趋势吗?
在初中,我们利用函数图象研究过函数值随自变量的增大而增大(或减小)的性质,这一性质叫做函数的单调性.
下面进一步用符号语言刻画这种性质.
先研究二次函数 f(x)=x2 的单调性.
如图,图象在y轴左侧部分从左到右是下降的,也就是说,当x<0时,y随x的增大而减小.
用符号语言描述:任意取x1,x2∈(-∞,0],得到f(x1)=x12,f(x2)=x22,那么
当x1<x2时,有f(x1)>f(x2).
这时我们就说函数 f(x)=x2 在区间(-∞,0]上是单调递减的.
如图,图象在y轴右侧部分从左到右是上升的,也就是说,当x>0时,y随x的增大而增大.
用符号语言描述:任意取x1,x2∈[0,+∞),得到f(x1)=x12,f(x2)=x22,那么
当x1<x2时,有f(x1)< f(x2).
这时我们就说函数 f(x)=x2 在区间[0,+∞)上是单调递增的.
思考:
函数f(x)=-x2 和 f(x)=各有怎样的单调性?
1
函数的单调性
一般地,设函数 f(x)的定义域为I,区间D I:
如果x1,x2∈D,当x1<x2时,都有f(x1)<f(x2),那么就称函数 f(x)在区间D上单调递增.
特别地,当函数 f(x)在它的定义域上单调递增时,我们就称它是增函数.
x
y
o
m
n
f(x1)
x1
x2
f(x2)
1
函数的单调性
一般地,设函数 f(x)的定义域为I,区间D I:
如果x1,x2∈D,当x1<x2时,都有f(x1)>f(x2),那么就称函数 f(x)在区间D上单调递减.
特别地,当函数 f(x)在它的定义域上单调递减时,我们就称它是减函数.
f(x1)
x1
x2
f(x2)
O
x
y
m
n
如果函数y=f(x)在区间D上单调递增或单调递减,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做y=f(x)的单调区间.
例1.上图是定义在区间[-5,5]上的函数y=f(x),根据图象说出函数的单调区间,以及在每一个单调区间上,它是增函数还是减函数
函数 f(x)= 有单调递减区间 ;
能否说 f(x)= 是单调递减函数?为什么?
思考
例2.根据定义证明以下各命题:
2
函数的单调性的证明
(1)函数f(x)= 在定义域上是增函数;
(2)函数 f(x)=-x3 在定义域上是减函数.
证明:(1)定义域为[0, + ∞).
x1,x2[0, + ∞),且x1
=
由x1
取点
作差
变形
定号
结论
例2.根据定义证明以下各命题:
2
函数的单调性的证明
(1)函数f(x)= 在定义域上是增函数;
(2)函数 f(x)=-x3 在定义域上是减函数
证明:(2)定义域为R.
x1,x2R,且x1
=(x2-x1)[(x2-x1)2+x12]
由x1
得 y1-y2 > 0 ,即y1>y2
所以,函数f(x)=-x3 在定义域上是减函数.
根据定义证明函数 f(x)=x+ 在[1, +∞)上是增函数.
练一练
知识篇
素养篇
思维篇
3.2.1 函数的单调性
1)函数y=x2-4x+5的单调区间是 .
问题系列:
答案:单调递增区间:[2, +∞)
单调递减区间:[-∞, 2)
2)函数y=x2-4x+5在区间(4, 5)上单调递增吗?
问题系列:
答案:单调递增
3)函数y=x2-4x+5的单调递增区间是(4, 5)吗?
问题系列:
答案:不是
4)函数y=x2-4x+5在区间(k, 5)上单调,则k∈ ;
问题系列:
答案:2
5)函数y=x2-4x+5在区间(k, k+3)上不单调,则
k∈ .
答案: -1
素养篇
思维篇
3.2.1 函数的单调性
1.若函数 的单调递减区间
为 ,则 a 的值为______.
答案:a=-3
2. 若函数 在区间
上是减函数,则实数 a 的取值范围是________.
答案:a≤-3
3. 若函数 f(x)是定义域为R的减函数,且 f(a-2)
答案:4. 若函数 f(x)定义域为[-1, 1],对于x1,x2[-1, 1],
<0恒成立,且f(a-2)
答案:
一、本节课学习的新知识
函数的单调性
单调区间
二、本节课提升的核心素养
数学抽象
数据分析
课堂小结
直观想象
数学建模
三、本节课训练的数学思想方法
分类讨论
课堂小结
数形结合
函数思想
01
基础作业: .
02
能力作业: .
03
拓展延伸:(选做)
作业
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
