2014高中数学二次函数的图像同步课时训练 北师大版必修1
文档属性
| 名称 | 2014高中数学二次函数的图像同步课时训练 北师大版必修1 |

|
|
| 格式 | zip | ||
| 文件大小 | 100.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-23 00:00:00 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
2014高中数学二次函数的图像同步课时训练 北师大版必修1
(30分钟 50分)
一、选择题(每小题4分,共16分)
1.(2012·上饶高一检测)f(x)=x2+ax+b满足f(1)=f(2)=0,则f(-1)的值为( )2·1·c·n·j·y
(A)5 (B)-5 (C)6 (D)-6【来源:21·世纪·教育·网】
2.已知函数y=ax2+bx+c(a≠0),如果a>b>c且a+b+c=0,则它的图像大致为
( )
( http: / / www.21cnjy.com )
3.二次函数y=6x2,y=-6x2,y=,y=-的图像共有的性质是( )
(A)开口向上 (B)对称轴是y轴
(C)都有最高点 (D)y随x的增大而增大
4.(易错题)已知二次函数y=kx2-7x-7的图像和x轴有交点,则k的取值范围是
( )
(A)k>- (B)k≥-且k≠0
(C)k≥- (D)k>-且k≠0
二、填空题(每小题4分,共8分)
5.若顶点坐标为(2,-2)的二次函数f ( http: / / www.21cnjy.com )(x)的图像与g(x)=-3(x+1)2的图像开口大小相同,方向相反,则二次函数f(x)的解析式为____________.www-2-1-cnjy-com
6.(2012·北京高一检测)将二次函数y=-2x2的顶点移到(-3,2)后,得到的函数的解析式为_____________.
三、解答题(每小题8分,共16分)
7.已知二次函数图像的顶点为(1,-3),且其图像与x轴的一个交点为(2,0),求此函数的解析式.
8.已知二次函数y=2x2-4x-6.
(1)求此函数图像的开口方向、对称轴、顶点坐标,并画出函数图像;
(2)求此函数图像与x轴、y轴的交点坐标,并求出以此三点为顶点的三角形的面积.
【挑战能力】
(10分)已知二次函数y=x2-2(m-1)x+m2-2m-3,其中m为实数.
(1)求证:不论m取何实数,这个二次函数的图像与x轴必有两个交点;
(2)设这个二次函数的图像与x轴交于点A(x1,0),B(x2,0),且x1、x2的倒数和为,求这个二次函数的解析式.2-1-c-n-j-y
答案解析
【解析】选C.∵f(1)=f(2)=0,∴解得
∴f(x)=x2-3x+2,
∴f(-1)=1+3+2=6.
2.【解析】选A.由a>b>c,a+b+c=0知a>0,c<0,且x=1时,y=0,故选A.
3.【解题指南】解答本题可从四个二次函数的图像与y=x2的图像的关系入手.
【解析】选B.因为四个二次函数的图像分别由函数y=x2的图像横坐标不变,纵坐标分别变为原来的6倍,-6倍,倍,-倍得到,因此四个函数图像的共同特征是对称轴均是y轴,故选B.21*cnjy*com
4.【解析】选B.因为二次函数y=kx2-7x-7的图像和x轴有交点,所以所以k≥-且k≠0,故选B.
【误区警示】解答本题时易忽视k≠0这一条件.因为当k=0时,函数y=kx2-7x-7不是二次函数,故解答此类题时一定要审好题.
5.【解析】由题意可知f(x)=3(x-2)2-2=3x2-12x+10.
答案:f(x)=3x2-12x+10
6.【解析】∵二次函数y=-2x2的顶点为 ( http: / / www.21cnjy.com )(0,0),∴要将其顶点移到(-3,2),只要把图像向左平移3个单位,向上平移2个单位即可,∴平移后的函数解析式为y=-2(x+3)2+2.
答案:y=-2(x+3)2+2
【变式训练】函数y=3x2-x+2的图像向左平移1个单位长度,再向下平移2个单位长度,所得图像对应的函数解析式是___________.
【解析】函数y=3x2-x+2的图像向左平移1个单位长度得到函数y=3(x+1)2-
(x+1)+2的图像,再向下平移2个单位长 ( http: / / www.21cnjy.com )度,得到函数y=3(x+1)2-(x+1)+2-2的图像,即所得图像对应的函数解析式是y=3x2+5x+2.
答案:y=3x2+5x+2
7.【解题指南】已知图像的两个点,如果用一般式,似乎差一个条件,但考虑到对称轴及顶点坐标公式,就可以列出三元一次方程组求解.
【解析】方法一:设所求函数的解析式为
y=ax2+bx+c(a≠0).
由题意得
所以函数的解析式为y=3x2-6x.
方法二:设所求函数的解析式为
y=ax2+bx+c(a≠0).
由题意得
由②得b=-2a, ④
把④代入③得c-a=-3, ⑤
把④代入①得c=0,把c=0代入⑤得a=3,
把a=3代入④得b=-6.
所以函数的解析式为y=3x2-6x.
方法三:设所求函数的解析式为y=a(x+h)2+k(a≠0),则顶点坐标为(-h,k).
∵顶点为(1,-3),∴h=-1,k=-3.
即所求的二次函数解析式为y=a(x-1)2-3.
∵图像经过点(2,0),∴0=a(2-1)2-3,∴a=3.
∴函数的解析式为y=3(x-1)2-3,
即y=3x2-6x.
方法四:设二次函数的解析式为y=a(x-x1)(x-x2)(a≠0),
其中x1,x2是抛物线与x轴两交点的横坐标.
∵抛物线与x轴的一个交点是(2,0),对称轴是x=1,
∴抛物线与x轴的另一个交点为(0,0),
∴x1=0,x2=2.
∴所求抛物线的解析式为y=a(x-0)(x-2)=ax(x-2).
又∵抛物线的顶点为(1,-3),
∴-3=a×1×(1-2),∴a=3.
∴函数的解析式为y=3x(x-2),
即y=3x2-6x.
【变式训练】已知二次函数y ( http: / / www.21cnjy.com )=ax2+bx+c(a≠0)的图像与x轴相交于点(-3,0),对称轴为x=-1,顶点M到x轴的距离为2,求此函数的解析式.www.21-cn-jy.com
【解析】方法一:因为二次函数图像的对称 ( http: / / www.21cnjy.com )轴是x=-1,又顶点M到x轴的距离为2,所以顶点的坐标为M(-1,2)或M′(-1,-2),故可设二次函数的解析式为y=a(x+1)2+2或y=a(x+1)2-2.【版权所有:21教育】
∵图像过点A(-3,0),
∴0=a(-3+1)2+2或0=a(-3+1)2-2,
解得a=-或a=.
故所求二次函数的解析式为
y=-(x+1)2+2或y=(x+1)2-2.
即y=-x2-x+或y=x2+x-.
方法二:因为二次函数图像的对称轴为 ( http: / / www.21cnjy.com )x=-1,又图像过点A(-3,0),所以点A关于对称轴的对称点A′(1,0)也在图像上,所以可设二次函数的解析式为y=a(x+3)(x-1)(a≠0),由题意得顶点坐标为(-1,2)或(-1,-2),分别代入上式.21cnjy.com
解得a=-或a=.
故所求二次函数的解析式为
y=-(x+3)(x-1)或y=(x+3)(x-1),
即y=-x2-x+或y=x2+x-.
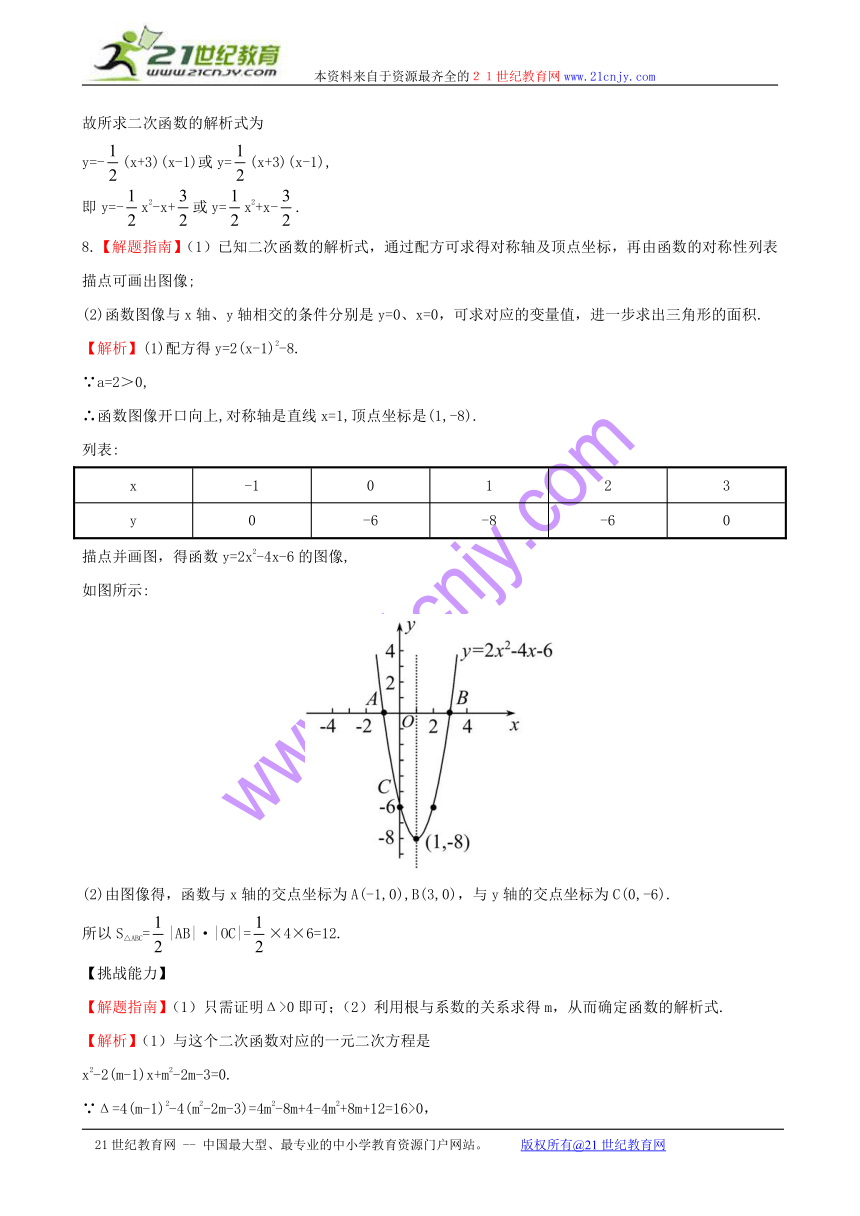
8.【解题指南】(1)已知二次函数的解析式,通过配方可求得对称轴及顶点坐标,再由函数的对称性列表描点可画出图像;
(2)函数图像与x轴、y轴相交的条件分别是y=0、x=0,可求对应的变量值,进一步求出三角形的面积.
【解析】(1)配方得y=2(x-1)2-8.
∵a=2>0,
∴函数图像开口向上,对称轴是直线x=1,顶点坐标是(1,-8).
列表:
x -1 0 1 2 3
y 0 -6 -8 -6 0
描点并画图,得函数y=2x2-4x-6的图像,
如图所示:
( http: / / www.21cnjy.com )
(2)由图像得,函数与x轴的交点坐标为A(-1,0),B(3,0),与y轴的交点坐标为C(0,-6).
所以S△ABC=|AB|·|OC|=×4×6=12.
【挑战能力】
【解题指南】(1)只需证明Δ>0即可;(2)利用根与系数的关系求得m,从而确定函数的解析式.
【解析】(1)与这个二次函数对应的一元二次方程是
x2-2(m-1)x+m2-2m-3=0.
∵Δ=4(m-1)2-4(m2-2m-3)=4m2-8m+4-4m2+8m+12=16>0,
∴方程x2-2(m-1)x+m2-2m-3=0必有两个不相等的实数根,
∴不论m取何实数,这个二次函数的图像与x轴必有两个交点.
(2)由题意可知,x1、x2是方程x2-2(m-1)x+m2-2m-3=0的两个不同的实数根,
∴x1+x2=2(m-1),x1·x2=m2-2m-3.
∵
∴ ①
解得m=0或m=5,经检验m=0,m=5都是方程①的解.
∴二次函数的解析式为y=x2+2x-3或y=x2-8x+12.
3.2 古典概型(第四、五课时)
3.2.1 —3.2.2古典概型及随机数的产生
一、教学目标:
1、知识与技能:(1)正确理解古典概型的两大特点:1)试验中所有可能出现的基本事件只有有限个;2)每个基本事件出现的可能性相等;
(2)掌握古典概型的概率计算公式:P(A)=
(3)了解随机数的概念;
(4)利用计算机产生随机数,并能直接统计出频数与频率。
2、过程与方法:(1)通过对现实生活中具 ( http: / / www.21cnjy.com )体的概率问题的探究,感知应用数学解决问题的方法,体会数学知识与现实世界的联系,培养逻辑推理能力;(2)通过模拟试验,感知应用数字解决问题的方法,自觉养成动手、动脑的良好习惯。21教育名师原创作品
3、情感态度与价值观:通过数学与探究活动,体会理论来源于实践并应用于实践的辩证唯物主义观点.
二、重点与难点:1、正确理解掌握古典概型及其概率公式;2、正确理解随机数的概念,并能应用计算机产生随机数.
三、学法与教学用具:1、与学生共同探讨,应用数学解决现实问题;2、通过模拟试验,感知应用数字解决问题的方法,自觉养成动手、动脑的良好习惯.
四、教学设想:
1、创设情境:(1)掷一枚质地均匀的硬币,结果只有2个,即“正面朝上”或“反面朝上”,它们都是随机事件。
(2)一个盒子中有10个完全相同的球,分别标以号码1,2,3,…,10,从中任取一球,只有10种不同的结果,即标号为1,2,3…,10。21·cn·jy·com
师生共同探讨:根据上述情况,你能发现它们有什么共同特点?
2、基本概念:
(1)基本事件、古典概率模型、随机数、伪随机数的概念见课本P121~126;
(2)古典概型的概率计算公式:P(A)=.
3、例题分析:
课本例题略
例1 掷一颗骰子,观察掷出的点数,求掷得奇数点的概率。
分析:掷骰子有6个基本事件,具有有限性和等可能性,因此是古典概型。
解:这个试验的基本事件共有6个,即(出现1点)、(出现2点)……、(出现6点)
所以基本事件数n=6,
事件A=(掷得奇数点)=(出现1点,出现3点,出现5点),
其包含的基本事件数m=3
所以,P(A)====0.5
小结:利用古典概型的计算公式时应注意两点:
(1)所有的基本事件必须是互斥的;
(2)m为事件A所包含的基本事件数,求m值时,要做到不重不漏。
例2 从含有两件正品a1,a2和一件次品b ( http: / / www.21cnjy.com )1的三件产品中,每次任取一件,每次取出后不放回,连续取两次,求取出的两件产品中恰有一件次品的概率。
解:每次取出一个,取后不放回地连续取两次, ( http: / / www.21cnjy.com )其一切可能的结果组成的基本事件有6个,即(a1,a2)和,(a1,b2),(a2,a1),(a2,b1),(b1,a1),(b2,a2)。其中小括号内左边的字母表示第1次取出的产品,右边的字母表示第2次取出的产用A表示“取出的两种中,恰好有一件次品”这一事件,则
A=[(a1,b1),(a2,b1),(b1,a1),(b1,a2)]
事件A由4个基本事件组成,因而,P(A)==
例3 现有一批产品共有10件,其中8件为正品,2件为次品:
(1)如果从中取出一件,然后放回,再取一件,求连续3次取出的都是正品的概率;
(2)如果从中一次取3件,求3件都是正品的概率.
分析:(1)为返回抽样;(2)为不返回抽样.
解:(1)有放回地抽取3次,按抽取顺序(x,y,z)记录结果,则x,y,z都有10种可能,所以试验结果有10×10×10=103种;设事件A为“连续3次都取正品”,则包含的基本事件共有8×8×8=83种,因此,P(A)= =0.512.【来源:21cnj*y.co*m】
(2)解法1:可以看作不放回抽样3次,顺序不同,基本事件不同,按抽取顺序记录(x,y,z),则x有10种可能,y有9种可能,z有8种可能,所以试验的所有结果为10×9×8=720种.设事件B为“3件都是正品”,则事件B包含的基本事件总数为8×7×6=336, 所以P(B)= ≈0.467.
解法2:可以看作不放回3次无顺序抽样,先按抽取顺序(x,y,z)记录结果,则x有10种可能,y有9种可能,z有8种可能,但(x,y,z),(x,z,y),(y,x,z),(y,z,x),(z,x,y),(z,y,x),是相同的,所以试验的所有结果有10×9×8÷6=120,按同样的方法,事件B包含的基本事件个数为8×7×6÷6=56,因此P(B)= ≈0.467.
小结:关于不放回抽样,计算 ( http: / / www.21cnjy.com )基本事件个数时,既可以看作是有顺序的,也可以看作是无顺序的,其结果是一样的,但不论选择哪一种方式,观察的角度必须一致,否则会导致错误.
例4 利用计算器产生10个1~100之间的取整数值的随机数。
解:具体操作如下:键入
反复操作10次即可得之
小结:利用计算器产生随机数,可以做随机模拟试验,在日常生活中,有着广泛的应用。
例5 某篮球爱好者,做投篮练习,假设其每次投篮命中的概率是40%,那么在连续三次投篮中,恰有两次投中的概率是多少?21教育网
分析:其投篮的可能结果有有限个,但是每 ( http: / / www.21cnjy.com )个结果的出现不是等可能的,所以不能用古典概型的概率公式计算,我们用计算机或计算器做模拟试验可以模拟投篮命中的概率为40%。21·世纪*教育网
解:我们通过设计模拟试验的方法来解决问题,利用计算机或计算器可以生产0到9之间的取整数值的随机数。
我们用1,2,3,4表示投中,用5 ( http: / / www.21cnjy.com ),6,7,8,9,0表示未投中,这样可以体现投中的概率是40%。因为是投篮三次,所以每三个随机数作为一组。 21*cnjy*com
例如:产生20组随机数:
812,932,569,683,271,989,730,537,925,
907,113,966,191,431,257,393,027,556.
这就相当于做了20次试验,在这组数中,如果恰有两个数在1,2,3,4中,则表示恰有两次投中,它们分别是812,932,271,191,393,即共有5个数,我们得到了三次投篮中恰有两次投中的概率近似为=25%。
小结:(1)利用计算机或计算器做随机模拟试验,可以解决非古典概型的概率的求解问题。
(2)对于上述试验,如果亲手做大量重复试验的话,花费的时间太多,因此利用计算机或计算器做随机模拟试验可以大大节省时间。
(3)随机函数RANDBETWEEN(a,b)产生从整数a到整数b的取整数值的随机数。
例6 你还知道哪些产生随机数的函数?请列举出来。
解:(1)每次按SHIFT RNA# 键都会产生一个0~1之间的随机数,而且出现0~1内任何一个数的可能性是相同的。
(2)还可以使用计算机软件来产生随 ( http: / / www.21cnjy.com )机数,如Scilab中产生随机数的方法。Scilab中用rand()函数来产生0~1之间的随机数,每周用一次rand()函数,就产生一个随机数,如果要产生a~b之间的随机数,可以使用变换rand()*(b-a)+a得到.
4、课堂小结:本节主要研究了古典概型的概率求法,解题时要注意两点:
(1)古典概型的使用条件:试验结果的有限性和所有结果的等可能性。
(2)古典概型的解题步骤;
①求出总的基本事件数;
②求出事件A所包含的基本事件数,然后利用公式P(A)=
(3)随机数量具有广泛的应用,可以帮助我们安 ( http: / / www.21cnjy.com )排和模拟一些试验,这样可以代替我们自己做大量重复试验,比如现在很多城市的重要考试采用产生随机数的方法把考生分配到各个考场中。
5、自我评价与课堂练习:
1.在40根纤维中,有12根的长度超过30mm,从中任取一根,取到长度超过30mm的纤维的概率是( )
A. B. C. D.以上都不对
2.盒中有10个铁钉,其中8个是合格的,2个是不合格的,从中任取一个恰为合格铁钉的概率是
A. B. C. D.
3.在大小相同的5个球中,2个是红球,3个是白球,若从中任取2个,则所取的2个球中至少有一个红球的概率是 。
4.抛掷2颗质地均匀的骰子,求点数和为8的概率。
5.利用计算器生产10个1到20之间的取整数值的随机数。
6.用0表示反面朝上,1表正面朝上,请用计算器做模拟掷硬币试验。
6、评价标准:
1.B[提示:在40根纤维中,有12根的长度超过30mm,即基本事件总数为40,且它们是等可能发生的,所求事件包含12个基本事件,故所求事件的概率为,因此选B.]21世纪教育网版权所有
2.C[提示:(方法1)从盒中任取一个铁钉包含基本事件总数为10,其中抽到合格铁订(记为事件A)包含8个基本事件,所以,所求概率为P(A)==.(方法2)本题还可以用对立事件的概率公式求解,因为从盒中任取一个铁钉,取到合格品(记为事件A)与取到不合格品(记为事件B)恰为对立事件,因此,P(A)=1-P(B)=1-=.]
3.[提示;记大小相同的5个球分别为红1,红2,白1,白2,白3,则基本事件为:(红1,红2),(红1,白1),(红1,白2)(红1,白3),(红2,白3),共10个,其中至少有一个红球的事件包括7个基本事件,所以,所求事件的概率为.本题还可以利用“对立事件的概率和为1”来求解,对于求“至多”“至少”等事件的概率头问题,常采用间接法,即求其对立事件的概率P(A),然后利用P(A)1-P(A)求解]。
4.解:在抛掷2颗骰子的试验中,每颗骰子均可出现1点,2点,…,6点6种不同的结果,我们把两颗骰子标上记号1,2以便区分,由于1号骰子的一个结果,因此同时掷两颗骰子的结果共有6×6=36种,在上面的所有结果中,向上的点数之和为8的结果有(2,6),(3,5),(4,4),(5,3),(6,2)5种,所以,所求事件的概率为.【出处:21教育名师】
5.解:具体操作如下
键入
反复按 键10次即可得到。
6.解:具体操作如下:
键入
7、作业:根据情况安排
PRB
RAND RANDI
STAT DEC
ENTER
RANDI(1,100)
STAT DEG
ENTER
RAND (1,100)
3.
STAT DEC
PRB
PAND RANDI
STAT DEG
ENTER
PANDI(1,20)
STAT DEG
ENTER
PANDI(1,20)
3.
STAT DEG
ENTER
PRB
PAND RANDI
STAT DEG
ENTER
PANDI(0,1)
STAT DEG
ENTER
PANDI(0,1)
0
STAT DEG
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
2014高中数学二次函数的图像同步课时训练 北师大版必修1
(30分钟 50分)
一、选择题(每小题4分,共16分)
1.(2012·上饶高一检测)f(x)=x2+ax+b满足f(1)=f(2)=0,则f(-1)的值为( )2·1·c·n·j·y
(A)5 (B)-5 (C)6 (D)-6【来源:21·世纪·教育·网】
2.已知函数y=ax2+bx+c(a≠0),如果a>b>c且a+b+c=0,则它的图像大致为
( )
( http: / / www.21cnjy.com )
3.二次函数y=6x2,y=-6x2,y=,y=-的图像共有的性质是( )
(A)开口向上 (B)对称轴是y轴
(C)都有最高点 (D)y随x的增大而增大
4.(易错题)已知二次函数y=kx2-7x-7的图像和x轴有交点,则k的取值范围是
( )
(A)k>- (B)k≥-且k≠0
(C)k≥- (D)k>-且k≠0
二、填空题(每小题4分,共8分)
5.若顶点坐标为(2,-2)的二次函数f ( http: / / www.21cnjy.com )(x)的图像与g(x)=-3(x+1)2的图像开口大小相同,方向相反,则二次函数f(x)的解析式为____________.www-2-1-cnjy-com
6.(2012·北京高一检测)将二次函数y=-2x2的顶点移到(-3,2)后,得到的函数的解析式为_____________.
三、解答题(每小题8分,共16分)
7.已知二次函数图像的顶点为(1,-3),且其图像与x轴的一个交点为(2,0),求此函数的解析式.
8.已知二次函数y=2x2-4x-6.
(1)求此函数图像的开口方向、对称轴、顶点坐标,并画出函数图像;
(2)求此函数图像与x轴、y轴的交点坐标,并求出以此三点为顶点的三角形的面积.
【挑战能力】
(10分)已知二次函数y=x2-2(m-1)x+m2-2m-3,其中m为实数.
(1)求证:不论m取何实数,这个二次函数的图像与x轴必有两个交点;
(2)设这个二次函数的图像与x轴交于点A(x1,0),B(x2,0),且x1、x2的倒数和为,求这个二次函数的解析式.2-1-c-n-j-y
答案解析
【解析】选C.∵f(1)=f(2)=0,∴解得
∴f(x)=x2-3x+2,
∴f(-1)=1+3+2=6.
2.【解析】选A.由a>b>c,a+b+c=0知a>0,c<0,且x=1时,y=0,故选A.
3.【解题指南】解答本题可从四个二次函数的图像与y=x2的图像的关系入手.
【解析】选B.因为四个二次函数的图像分别由函数y=x2的图像横坐标不变,纵坐标分别变为原来的6倍,-6倍,倍,-倍得到,因此四个函数图像的共同特征是对称轴均是y轴,故选B.21*cnjy*com
4.【解析】选B.因为二次函数y=kx2-7x-7的图像和x轴有交点,所以所以k≥-且k≠0,故选B.
【误区警示】解答本题时易忽视k≠0这一条件.因为当k=0时,函数y=kx2-7x-7不是二次函数,故解答此类题时一定要审好题.
5.【解析】由题意可知f(x)=3(x-2)2-2=3x2-12x+10.
答案:f(x)=3x2-12x+10
6.【解析】∵二次函数y=-2x2的顶点为 ( http: / / www.21cnjy.com )(0,0),∴要将其顶点移到(-3,2),只要把图像向左平移3个单位,向上平移2个单位即可,∴平移后的函数解析式为y=-2(x+3)2+2.
答案:y=-2(x+3)2+2
【变式训练】函数y=3x2-x+2的图像向左平移1个单位长度,再向下平移2个单位长度,所得图像对应的函数解析式是___________.
【解析】函数y=3x2-x+2的图像向左平移1个单位长度得到函数y=3(x+1)2-
(x+1)+2的图像,再向下平移2个单位长 ( http: / / www.21cnjy.com )度,得到函数y=3(x+1)2-(x+1)+2-2的图像,即所得图像对应的函数解析式是y=3x2+5x+2.
答案:y=3x2+5x+2
7.【解题指南】已知图像的两个点,如果用一般式,似乎差一个条件,但考虑到对称轴及顶点坐标公式,就可以列出三元一次方程组求解.
【解析】方法一:设所求函数的解析式为
y=ax2+bx+c(a≠0).
由题意得
所以函数的解析式为y=3x2-6x.
方法二:设所求函数的解析式为
y=ax2+bx+c(a≠0).
由题意得
由②得b=-2a, ④
把④代入③得c-a=-3, ⑤
把④代入①得c=0,把c=0代入⑤得a=3,
把a=3代入④得b=-6.
所以函数的解析式为y=3x2-6x.
方法三:设所求函数的解析式为y=a(x+h)2+k(a≠0),则顶点坐标为(-h,k).
∵顶点为(1,-3),∴h=-1,k=-3.
即所求的二次函数解析式为y=a(x-1)2-3.
∵图像经过点(2,0),∴0=a(2-1)2-3,∴a=3.
∴函数的解析式为y=3(x-1)2-3,
即y=3x2-6x.
方法四:设二次函数的解析式为y=a(x-x1)(x-x2)(a≠0),
其中x1,x2是抛物线与x轴两交点的横坐标.
∵抛物线与x轴的一个交点是(2,0),对称轴是x=1,
∴抛物线与x轴的另一个交点为(0,0),
∴x1=0,x2=2.
∴所求抛物线的解析式为y=a(x-0)(x-2)=ax(x-2).
又∵抛物线的顶点为(1,-3),
∴-3=a×1×(1-2),∴a=3.
∴函数的解析式为y=3x(x-2),
即y=3x2-6x.
【变式训练】已知二次函数y ( http: / / www.21cnjy.com )=ax2+bx+c(a≠0)的图像与x轴相交于点(-3,0),对称轴为x=-1,顶点M到x轴的距离为2,求此函数的解析式.www.21-cn-jy.com
【解析】方法一:因为二次函数图像的对称 ( http: / / www.21cnjy.com )轴是x=-1,又顶点M到x轴的距离为2,所以顶点的坐标为M(-1,2)或M′(-1,-2),故可设二次函数的解析式为y=a(x+1)2+2或y=a(x+1)2-2.【版权所有:21教育】
∵图像过点A(-3,0),
∴0=a(-3+1)2+2或0=a(-3+1)2-2,
解得a=-或a=.
故所求二次函数的解析式为
y=-(x+1)2+2或y=(x+1)2-2.
即y=-x2-x+或y=x2+x-.
方法二:因为二次函数图像的对称轴为 ( http: / / www.21cnjy.com )x=-1,又图像过点A(-3,0),所以点A关于对称轴的对称点A′(1,0)也在图像上,所以可设二次函数的解析式为y=a(x+3)(x-1)(a≠0),由题意得顶点坐标为(-1,2)或(-1,-2),分别代入上式.21cnjy.com
解得a=-或a=.
故所求二次函数的解析式为
y=-(x+3)(x-1)或y=(x+3)(x-1),
即y=-x2-x+或y=x2+x-.
8.【解题指南】(1)已知二次函数的解析式,通过配方可求得对称轴及顶点坐标,再由函数的对称性列表描点可画出图像;
(2)函数图像与x轴、y轴相交的条件分别是y=0、x=0,可求对应的变量值,进一步求出三角形的面积.
【解析】(1)配方得y=2(x-1)2-8.
∵a=2>0,
∴函数图像开口向上,对称轴是直线x=1,顶点坐标是(1,-8).
列表:
x -1 0 1 2 3
y 0 -6 -8 -6 0
描点并画图,得函数y=2x2-4x-6的图像,
如图所示:
( http: / / www.21cnjy.com )
(2)由图像得,函数与x轴的交点坐标为A(-1,0),B(3,0),与y轴的交点坐标为C(0,-6).
所以S△ABC=|AB|·|OC|=×4×6=12.
【挑战能力】
【解题指南】(1)只需证明Δ>0即可;(2)利用根与系数的关系求得m,从而确定函数的解析式.
【解析】(1)与这个二次函数对应的一元二次方程是
x2-2(m-1)x+m2-2m-3=0.
∵Δ=4(m-1)2-4(m2-2m-3)=4m2-8m+4-4m2+8m+12=16>0,
∴方程x2-2(m-1)x+m2-2m-3=0必有两个不相等的实数根,
∴不论m取何实数,这个二次函数的图像与x轴必有两个交点.
(2)由题意可知,x1、x2是方程x2-2(m-1)x+m2-2m-3=0的两个不同的实数根,
∴x1+x2=2(m-1),x1·x2=m2-2m-3.
∵
∴ ①
解得m=0或m=5,经检验m=0,m=5都是方程①的解.
∴二次函数的解析式为y=x2+2x-3或y=x2-8x+12.
3.2 古典概型(第四、五课时)
3.2.1 —3.2.2古典概型及随机数的产生
一、教学目标:
1、知识与技能:(1)正确理解古典概型的两大特点:1)试验中所有可能出现的基本事件只有有限个;2)每个基本事件出现的可能性相等;
(2)掌握古典概型的概率计算公式:P(A)=
(3)了解随机数的概念;
(4)利用计算机产生随机数,并能直接统计出频数与频率。
2、过程与方法:(1)通过对现实生活中具 ( http: / / www.21cnjy.com )体的概率问题的探究,感知应用数学解决问题的方法,体会数学知识与现实世界的联系,培养逻辑推理能力;(2)通过模拟试验,感知应用数字解决问题的方法,自觉养成动手、动脑的良好习惯。21教育名师原创作品
3、情感态度与价值观:通过数学与探究活动,体会理论来源于实践并应用于实践的辩证唯物主义观点.
二、重点与难点:1、正确理解掌握古典概型及其概率公式;2、正确理解随机数的概念,并能应用计算机产生随机数.
三、学法与教学用具:1、与学生共同探讨,应用数学解决现实问题;2、通过模拟试验,感知应用数字解决问题的方法,自觉养成动手、动脑的良好习惯.
四、教学设想:
1、创设情境:(1)掷一枚质地均匀的硬币,结果只有2个,即“正面朝上”或“反面朝上”,它们都是随机事件。
(2)一个盒子中有10个完全相同的球,分别标以号码1,2,3,…,10,从中任取一球,只有10种不同的结果,即标号为1,2,3…,10。21·cn·jy·com
师生共同探讨:根据上述情况,你能发现它们有什么共同特点?
2、基本概念:
(1)基本事件、古典概率模型、随机数、伪随机数的概念见课本P121~126;
(2)古典概型的概率计算公式:P(A)=.
3、例题分析:
课本例题略
例1 掷一颗骰子,观察掷出的点数,求掷得奇数点的概率。
分析:掷骰子有6个基本事件,具有有限性和等可能性,因此是古典概型。
解:这个试验的基本事件共有6个,即(出现1点)、(出现2点)……、(出现6点)
所以基本事件数n=6,
事件A=(掷得奇数点)=(出现1点,出现3点,出现5点),
其包含的基本事件数m=3
所以,P(A)====0.5
小结:利用古典概型的计算公式时应注意两点:
(1)所有的基本事件必须是互斥的;
(2)m为事件A所包含的基本事件数,求m值时,要做到不重不漏。
例2 从含有两件正品a1,a2和一件次品b ( http: / / www.21cnjy.com )1的三件产品中,每次任取一件,每次取出后不放回,连续取两次,求取出的两件产品中恰有一件次品的概率。
解:每次取出一个,取后不放回地连续取两次, ( http: / / www.21cnjy.com )其一切可能的结果组成的基本事件有6个,即(a1,a2)和,(a1,b2),(a2,a1),(a2,b1),(b1,a1),(b2,a2)。其中小括号内左边的字母表示第1次取出的产品,右边的字母表示第2次取出的产用A表示“取出的两种中,恰好有一件次品”这一事件,则
A=[(a1,b1),(a2,b1),(b1,a1),(b1,a2)]
事件A由4个基本事件组成,因而,P(A)==
例3 现有一批产品共有10件,其中8件为正品,2件为次品:
(1)如果从中取出一件,然后放回,再取一件,求连续3次取出的都是正品的概率;
(2)如果从中一次取3件,求3件都是正品的概率.
分析:(1)为返回抽样;(2)为不返回抽样.
解:(1)有放回地抽取3次,按抽取顺序(x,y,z)记录结果,则x,y,z都有10种可能,所以试验结果有10×10×10=103种;设事件A为“连续3次都取正品”,则包含的基本事件共有8×8×8=83种,因此,P(A)= =0.512.【来源:21cnj*y.co*m】
(2)解法1:可以看作不放回抽样3次,顺序不同,基本事件不同,按抽取顺序记录(x,y,z),则x有10种可能,y有9种可能,z有8种可能,所以试验的所有结果为10×9×8=720种.设事件B为“3件都是正品”,则事件B包含的基本事件总数为8×7×6=336, 所以P(B)= ≈0.467.
解法2:可以看作不放回3次无顺序抽样,先按抽取顺序(x,y,z)记录结果,则x有10种可能,y有9种可能,z有8种可能,但(x,y,z),(x,z,y),(y,x,z),(y,z,x),(z,x,y),(z,y,x),是相同的,所以试验的所有结果有10×9×8÷6=120,按同样的方法,事件B包含的基本事件个数为8×7×6÷6=56,因此P(B)= ≈0.467.
小结:关于不放回抽样,计算 ( http: / / www.21cnjy.com )基本事件个数时,既可以看作是有顺序的,也可以看作是无顺序的,其结果是一样的,但不论选择哪一种方式,观察的角度必须一致,否则会导致错误.
例4 利用计算器产生10个1~100之间的取整数值的随机数。
解:具体操作如下:键入
反复操作10次即可得之
小结:利用计算器产生随机数,可以做随机模拟试验,在日常生活中,有着广泛的应用。
例5 某篮球爱好者,做投篮练习,假设其每次投篮命中的概率是40%,那么在连续三次投篮中,恰有两次投中的概率是多少?21教育网
分析:其投篮的可能结果有有限个,但是每 ( http: / / www.21cnjy.com )个结果的出现不是等可能的,所以不能用古典概型的概率公式计算,我们用计算机或计算器做模拟试验可以模拟投篮命中的概率为40%。21·世纪*教育网
解:我们通过设计模拟试验的方法来解决问题,利用计算机或计算器可以生产0到9之间的取整数值的随机数。
我们用1,2,3,4表示投中,用5 ( http: / / www.21cnjy.com ),6,7,8,9,0表示未投中,这样可以体现投中的概率是40%。因为是投篮三次,所以每三个随机数作为一组。 21*cnjy*com
例如:产生20组随机数:
812,932,569,683,271,989,730,537,925,
907,113,966,191,431,257,393,027,556.
这就相当于做了20次试验,在这组数中,如果恰有两个数在1,2,3,4中,则表示恰有两次投中,它们分别是812,932,271,191,393,即共有5个数,我们得到了三次投篮中恰有两次投中的概率近似为=25%。
小结:(1)利用计算机或计算器做随机模拟试验,可以解决非古典概型的概率的求解问题。
(2)对于上述试验,如果亲手做大量重复试验的话,花费的时间太多,因此利用计算机或计算器做随机模拟试验可以大大节省时间。
(3)随机函数RANDBETWEEN(a,b)产生从整数a到整数b的取整数值的随机数。
例6 你还知道哪些产生随机数的函数?请列举出来。
解:(1)每次按SHIFT RNA# 键都会产生一个0~1之间的随机数,而且出现0~1内任何一个数的可能性是相同的。
(2)还可以使用计算机软件来产生随 ( http: / / www.21cnjy.com )机数,如Scilab中产生随机数的方法。Scilab中用rand()函数来产生0~1之间的随机数,每周用一次rand()函数,就产生一个随机数,如果要产生a~b之间的随机数,可以使用变换rand()*(b-a)+a得到.
4、课堂小结:本节主要研究了古典概型的概率求法,解题时要注意两点:
(1)古典概型的使用条件:试验结果的有限性和所有结果的等可能性。
(2)古典概型的解题步骤;
①求出总的基本事件数;
②求出事件A所包含的基本事件数,然后利用公式P(A)=
(3)随机数量具有广泛的应用,可以帮助我们安 ( http: / / www.21cnjy.com )排和模拟一些试验,这样可以代替我们自己做大量重复试验,比如现在很多城市的重要考试采用产生随机数的方法把考生分配到各个考场中。
5、自我评价与课堂练习:
1.在40根纤维中,有12根的长度超过30mm,从中任取一根,取到长度超过30mm的纤维的概率是( )
A. B. C. D.以上都不对
2.盒中有10个铁钉,其中8个是合格的,2个是不合格的,从中任取一个恰为合格铁钉的概率是
A. B. C. D.
3.在大小相同的5个球中,2个是红球,3个是白球,若从中任取2个,则所取的2个球中至少有一个红球的概率是 。
4.抛掷2颗质地均匀的骰子,求点数和为8的概率。
5.利用计算器生产10个1到20之间的取整数值的随机数。
6.用0表示反面朝上,1表正面朝上,请用计算器做模拟掷硬币试验。
6、评价标准:
1.B[提示:在40根纤维中,有12根的长度超过30mm,即基本事件总数为40,且它们是等可能发生的,所求事件包含12个基本事件,故所求事件的概率为,因此选B.]21世纪教育网版权所有
2.C[提示:(方法1)从盒中任取一个铁钉包含基本事件总数为10,其中抽到合格铁订(记为事件A)包含8个基本事件,所以,所求概率为P(A)==.(方法2)本题还可以用对立事件的概率公式求解,因为从盒中任取一个铁钉,取到合格品(记为事件A)与取到不合格品(记为事件B)恰为对立事件,因此,P(A)=1-P(B)=1-=.]
3.[提示;记大小相同的5个球分别为红1,红2,白1,白2,白3,则基本事件为:(红1,红2),(红1,白1),(红1,白2)(红1,白3),(红2,白3),共10个,其中至少有一个红球的事件包括7个基本事件,所以,所求事件的概率为.本题还可以利用“对立事件的概率和为1”来求解,对于求“至多”“至少”等事件的概率头问题,常采用间接法,即求其对立事件的概率P(A),然后利用P(A)1-P(A)求解]。
4.解:在抛掷2颗骰子的试验中,每颗骰子均可出现1点,2点,…,6点6种不同的结果,我们把两颗骰子标上记号1,2以便区分,由于1号骰子的一个结果,因此同时掷两颗骰子的结果共有6×6=36种,在上面的所有结果中,向上的点数之和为8的结果有(2,6),(3,5),(4,4),(5,3),(6,2)5种,所以,所求事件的概率为.【出处:21教育名师】
5.解:具体操作如下
键入
反复按 键10次即可得到。
6.解:具体操作如下:
键入
7、作业:根据情况安排
PRB
RAND RANDI
STAT DEC
ENTER
RANDI(1,100)
STAT DEG
ENTER
RAND (1,100)
3.
STAT DEC
PRB
PAND RANDI
STAT DEG
ENTER
PANDI(1,20)
STAT DEG
ENTER
PANDI(1,20)
3.
STAT DEG
ENTER
PRB
PAND RANDI
STAT DEG
ENTER
PANDI(0,1)
STAT DEG
ENTER
PANDI(0,1)
0
STAT DEG
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
