4.1 光的折射 课件 (共33张PPT)
文档属性
| 名称 | 4.1 光的折射 课件 (共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 93.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-09-11 16:49:53 | ||
图片预览








文档简介
(共33张PPT)
第四章 光
第1节 光的折射
课堂引入
射水鱼在水中能准确射中水面上不远处的小昆虫。水中的鱼看到小昆虫在什么位置?是在昆虫的上方还是下方?
铅笔折断了吗?
海市蜃楼是怎么形成的?
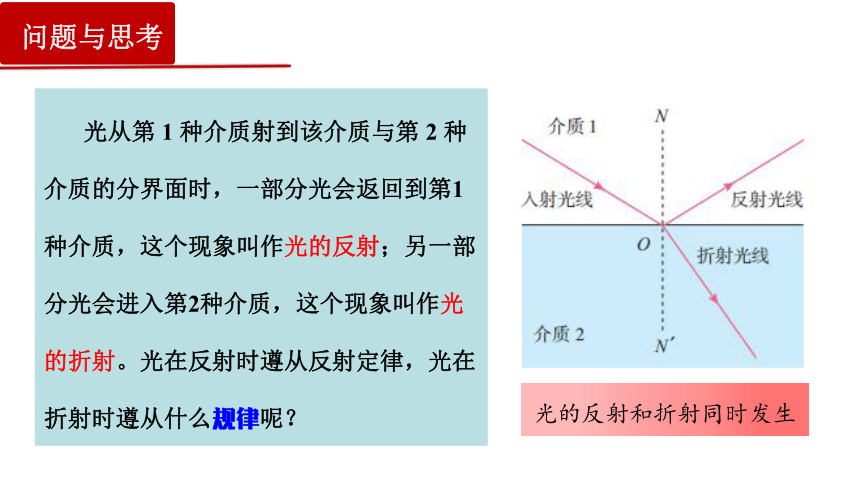
光从第 1 种介质射到该介质与第 2 种介质的分界面时,一部分光会返回到第1种介质,这个现象叫作光的反射;另一部分光会进入第2种介质,这个现象叫作光的折射。光在反射时遵从反射定律,光在折射时遵从什么规律呢?
光的反射和折射同时发生
问题与思考
界面
入射光线
反射光线
法线
入射角
反射角
1.光的反射:光照射到两种介质的界面上,一部分返回原来介质的现象。
(1)反射光线与入射光线、法线在同一平面内;(2)反射光线和入射光线分居法线两侧:(3)反射角等于入射角.
光路可逆
一、光的反射
2.光的反射定律:
光的折射:光从一种介质斜射入另一种介质时,传播方向发生改变的现象。
二、光的折射
θ1
θ2
空气
玻璃
N
N'
A
O
B
光的折射规律
二、光的折射
N
N′
空气
玻璃
i
r
O
A
B
界面
法线
入射光线
折射光线
入射角
折射角
(
(
反射光线
1.折射光线、入射光线、法线在同一平面内
2.折射光线和入射光线分居法线两侧
3.当光从空气斜射入玻璃中时,折射角小于入射角
4.当光从玻璃斜射入空气中时,折射角大于入射角
5.当入射角增大时,折射角也随着增大
二、光的折射
入射角与折射角有什么定量关系呢?
入射角i
10
30
40
50
60
70
80
折射角r
6.6
19.5
25.4
30.7
35.3
38.8
41.1
i / r
1.51
1.54
1.57
1.63
1.70
1.80
1.95
sini/sinr
1.51
1.50
1.50
1.50
1.50
1.50
1.50
=n(n为常数)
实验结论:入射角的正弦跟折射角的正弦成正比
以光从空气射入玻璃为例
折射角和入射角的关系
二、光的折射
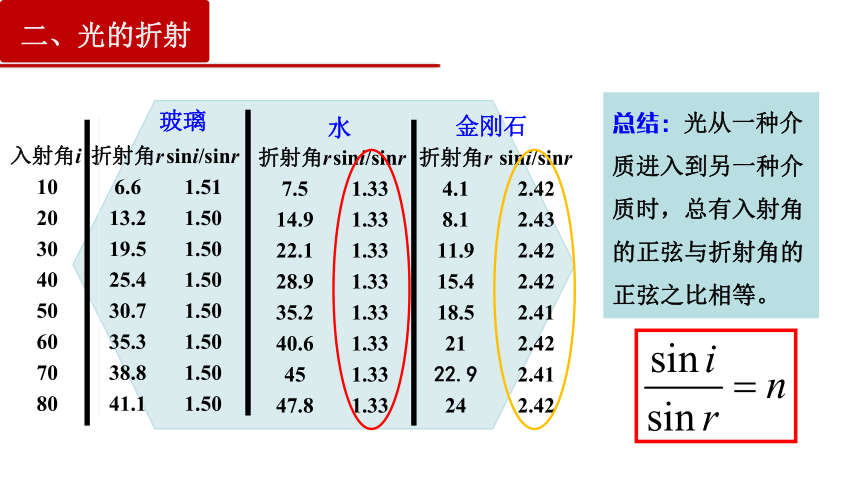
思考:如果将玻璃换成其它介质,入射角和折射角的正弦之比是否具有相同的结论?
sini/sinr
1.51
1.50
1.50
1.50
1.50
1.50
1.50
1.50
入射角i
10
20
30
40
50
60
70
80
折射角r
6.6
13.2
19.5
25.4
30.7
35.3
38.8
41.1
玻璃
水
折射角r
7.5
14.9
22.1
28.9
35.2
40.6
45
47.8
sini/sinr
1.33
1.33
1.33
1.33
1.33
1.33
1.33
1.33
金刚石
折射角r
4.1
8.1
11.9
15.4
18.5
21
22.9
24
sini/sinr
2.42
2.43
2.42
2.42
2.41
2.42
2.41
2.42
总结:光从一种介质进入到另一种介质时,总有入射角的正弦与折射角的正弦之比相等。
二、光的折射
斯涅耳
1621 年,荷兰数学家斯涅耳在分析了大量实验数据后,找到了两者
之间的关系,并把它总结为光的折射定律(refraction law):
二、光的折射
入射光线、法线处在同一平面内,折射光线与入射光线分别位于法线的两侧;入射角的正弦与折射角的正弦成正比,即:
说明:
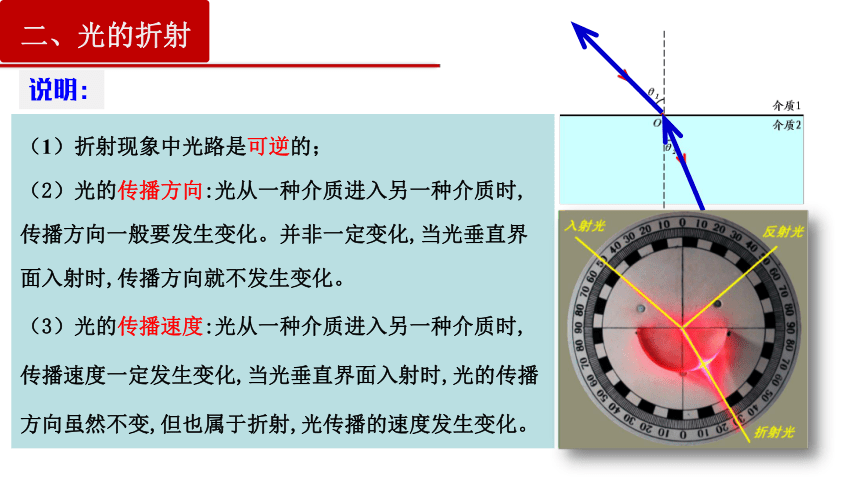
(1)折射现象中光路是可逆的;
(2)光的传播方向:光从一种介质进入另一种介质时,传播方向一般要发生变化。并非一定变化,当光垂直界面入射时,传播方向就不发生变化。
(3)光的传播速度:光从一种介质进入另一种介质时,传播速度一定发生变化,当光垂直界面入射时,光的传播方向虽然不变,但也属于折射,光传播的速度发生变化。
二、光的折射
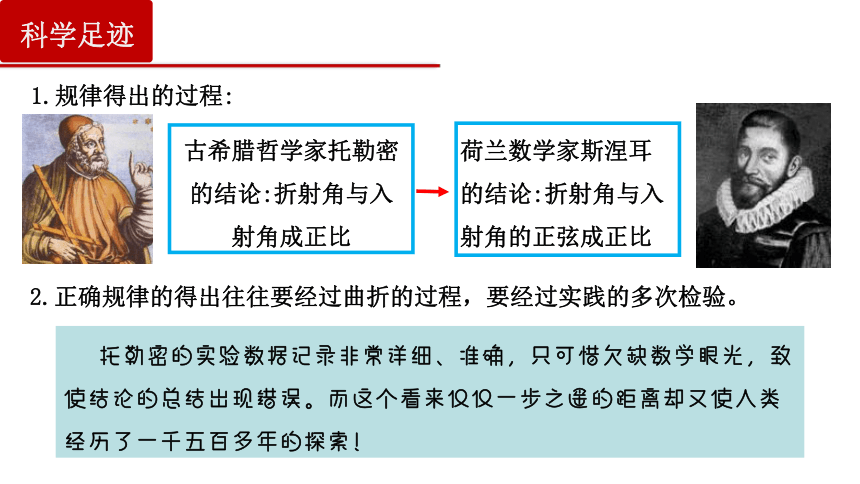
1.规律得出的过程:
2.正确规律的得出往往要经过曲折的过程,要经过实践的多次检验。
古希腊哲学家托勒密的结论:折射角与入射角成正比
托勒密的实验数据记录非常详细、准确,只可惜欠缺数学眼光,致使结论的总结出现错误。而这个看来仅仅一步之遥的距离却又使人类经历了一千五百多年的探索!
科学足迹
荷兰数学家斯涅耳的结论:折射角与入射角的正弦成正比
说明:(1)n的大小与θ1和θ2无关,与介质和入射光
的频率有关,对于确定的介质,n是定值,不能说n∝sinθ1或n∝1/sinθ2
(2)折射率无单位,任何介质的折射率皆大于1。
2.定义式:
1.定义:光从真空射入某种介质发生折射时,入射角的正弦与折射角的正弦之比,叫做这种介质的绝对折射率,简称折射率。用符号 n 表示。
(3)折射率反映介质对光的偏折作用,n越大光线偏折越厉害。
三、折射率
(4)光从一种介质进入另一种介质时,折射角与入射角的大小关系不要一概而论,要视两种介质的折射率大小而定。
(5)当光从折射率小的介质斜射入折射率大的介质时,入射角大于折射角,当光从折射率大的介质斜射入折射率小的介质时,入射角小于折射角。
三、折射率
空气对光的传播影响很小,可以作为真空处理
由于光的折射,水中物体的位置看起来比实际位置要高些。
应用1:渔民叉鱼
渔民怎样才能叉到鱼?
四、生活中的折射现象
高
水
看到的气球在折射光线的反向延长线上.
空气
应用2:在水下看水面上的物体比实际位置高还是低?
四、生活中的折射现象
应用3:铅笔弯折之谜
空气
水
A
A
界面
四、生活中的折射现象
应用4:井中的青蛙看岸上的物体的位置偏向哪里?
偏向上方
井中的青蛙看井口的宽度是偏大还是偏小?
偏小
四、生活中的折射现象
SS′有大气,看到太阳更早没有大气,将迟一些看到太阳四、生活中的折射现象应用5:蒙气差现象
四、生活中的折射现象
1.常规思路
(1)根据题意画出正确的光路图.
(2)利用几何关系确定光路图中的边、角关系,要注意入射角、折射角均是与法线的夹角.
(3)利用折射定律、折射率公式列式求解.
解决光的折射问题的常规思路
2.视深问题
(1)视深是人眼看透明物质内部某物点时像点离界面的距离.在中学阶段,一般都是沿着界面的法线方向去观察,在计算时,由于入射角很小,折射角也很小,故有 ,这是在视深问题中经常用到的关系式.
(2)当沿竖直方向看水中物体时,“视深”是实际深度的倍,n是水的折射率.
解决光的折射问题的视深问题
课堂小结
光的
折射
折射率
光的折射:光从一种介质斜射入另一种介质时,传播方向发生改变的现象。
入射光线、法线处在同一平面内,折射光线与入射光线分别位于法线的两侧;入射角的正弦与折射角的正弦成正比,即:
光从真空射入某种介质发生折射时,入射角的正弦与折射角的正弦之比,叫做这种介质的绝对折射率,简称折射率。用符号 n 表示。
【典例1】如图所示是光线以相同的入射角从空气射入三种不同介质时的折射情况,则在三种介质中光的传播速度最小的是( )
A.介质甲 B.介质乙 C.介质丙 D.三种介质均一样
【正确答案】C
典例分析
【典例2】光在某种玻璃中的传播速度是 ,要使光由玻璃射入空气时折射光线与反射光线成90°,则入射光线与反射光线的夹角成( )
A.30° B.60° C.45° D.90°
【正确答案】B
典例分析
【典例3】物理社团的同学想测量一透明物体的折射率。如图所示,透明物体左右两侧紧靠遮光板,右下方压着一片小树叶,观察点距离透明物体左上边缘的高度为h、水平距离为2h时,恰好看到树叶。移走透明物体(小树叶和遮光板的位置不动),观察点水平向右移动,当水平移动距离 时,恰好又看到小树叶。则透明物体的折射率为( )
A. B. C. D.2
【正确答案】D
典例分析
【典例4】光线以60°的入射角从空气射入玻璃中,折射光线与反射光线恰好垂直。(真空中的光速c=3.0×108 m/s)
(1)画出折射光路图;
(2)求出玻璃的折射率和光在玻璃中的传播速度大小;
(3)当入射角变为45°时,折射角的正弦值是多大
(4)当入射角增大或减小时,玻璃的折射率是否变化
典例分析
【解析】 (1)由题意知入射角θ1=60°,反射角θ'=60°,折射角
θ2=180°-60°-90°=30°,光路图如图所示。
(4)折射率不会变化,折射率由介质和入射光线的频率决定,跟入射角的大小无关。
【典例5】如图所示,一束激光垂直于AC面照射到等边玻璃三棱镜的AB面上。已知AB面的反射光线与折射光线的夹角为90°。光在真空中的传播速度为c。求:(1)玻璃的折射率;
(2)激光在玻璃中传播的速度。
典例分析
【典例6】如图所示,一小孩站在宽6 m的河边,在他正对面的岸边有一距离河面高度为3 m的树,树的正下方河底有一块石头,小孩向河面看去,可同时看到树顶和石头两者的像,并发现两个像重合,若小孩的眼睛离河面高为1.5 m,河水的折射率为 ,试估算河水深度。
典例分析
【答案】 5.3 m
【解析】树顶反射和石头折射成像的光路图如图所示
第四章 光
第1节 光的折射
课堂引入
射水鱼在水中能准确射中水面上不远处的小昆虫。水中的鱼看到小昆虫在什么位置?是在昆虫的上方还是下方?
铅笔折断了吗?
海市蜃楼是怎么形成的?
光从第 1 种介质射到该介质与第 2 种介质的分界面时,一部分光会返回到第1种介质,这个现象叫作光的反射;另一部分光会进入第2种介质,这个现象叫作光的折射。光在反射时遵从反射定律,光在折射时遵从什么规律呢?
光的反射和折射同时发生
问题与思考
界面
入射光线
反射光线
法线
入射角
反射角
1.光的反射:光照射到两种介质的界面上,一部分返回原来介质的现象。
(1)反射光线与入射光线、法线在同一平面内;(2)反射光线和入射光线分居法线两侧:(3)反射角等于入射角.
光路可逆
一、光的反射
2.光的反射定律:
光的折射:光从一种介质斜射入另一种介质时,传播方向发生改变的现象。
二、光的折射
θ1
θ2
空气
玻璃
N
N'
A
O
B
光的折射规律
二、光的折射
N
N′
空气
玻璃
i
r
O
A
B
界面
法线
入射光线
折射光线
入射角
折射角
(
(
反射光线
1.折射光线、入射光线、法线在同一平面内
2.折射光线和入射光线分居法线两侧
3.当光从空气斜射入玻璃中时,折射角小于入射角
4.当光从玻璃斜射入空气中时,折射角大于入射角
5.当入射角增大时,折射角也随着增大
二、光的折射
入射角与折射角有什么定量关系呢?
入射角i
10
30
40
50
60
70
80
折射角r
6.6
19.5
25.4
30.7
35.3
38.8
41.1
i / r
1.51
1.54
1.57
1.63
1.70
1.80
1.95
sini/sinr
1.51
1.50
1.50
1.50
1.50
1.50
1.50
=n(n为常数)
实验结论:入射角的正弦跟折射角的正弦成正比
以光从空气射入玻璃为例
折射角和入射角的关系
二、光的折射
思考:如果将玻璃换成其它介质,入射角和折射角的正弦之比是否具有相同的结论?
sini/sinr
1.51
1.50
1.50
1.50
1.50
1.50
1.50
1.50
入射角i
10
20
30
40
50
60
70
80
折射角r
6.6
13.2
19.5
25.4
30.7
35.3
38.8
41.1
玻璃
水
折射角r
7.5
14.9
22.1
28.9
35.2
40.6
45
47.8
sini/sinr
1.33
1.33
1.33
1.33
1.33
1.33
1.33
1.33
金刚石
折射角r
4.1
8.1
11.9
15.4
18.5
21
22.9
24
sini/sinr
2.42
2.43
2.42
2.42
2.41
2.42
2.41
2.42
总结:光从一种介质进入到另一种介质时,总有入射角的正弦与折射角的正弦之比相等。
二、光的折射
斯涅耳
1621 年,荷兰数学家斯涅耳在分析了大量实验数据后,找到了两者
之间的关系,并把它总结为光的折射定律(refraction law):
二、光的折射
入射光线、法线处在同一平面内,折射光线与入射光线分别位于法线的两侧;入射角的正弦与折射角的正弦成正比,即:
说明:
(1)折射现象中光路是可逆的;
(2)光的传播方向:光从一种介质进入另一种介质时,传播方向一般要发生变化。并非一定变化,当光垂直界面入射时,传播方向就不发生变化。
(3)光的传播速度:光从一种介质进入另一种介质时,传播速度一定发生变化,当光垂直界面入射时,光的传播方向虽然不变,但也属于折射,光传播的速度发生变化。
二、光的折射
1.规律得出的过程:
2.正确规律的得出往往要经过曲折的过程,要经过实践的多次检验。
古希腊哲学家托勒密的结论:折射角与入射角成正比
托勒密的实验数据记录非常详细、准确,只可惜欠缺数学眼光,致使结论的总结出现错误。而这个看来仅仅一步之遥的距离却又使人类经历了一千五百多年的探索!
科学足迹
荷兰数学家斯涅耳的结论:折射角与入射角的正弦成正比
说明:(1)n的大小与θ1和θ2无关,与介质和入射光
的频率有关,对于确定的介质,n是定值,不能说n∝sinθ1或n∝1/sinθ2
(2)折射率无单位,任何介质的折射率皆大于1。
2.定义式:
1.定义:光从真空射入某种介质发生折射时,入射角的正弦与折射角的正弦之比,叫做这种介质的绝对折射率,简称折射率。用符号 n 表示。
(3)折射率反映介质对光的偏折作用,n越大光线偏折越厉害。
三、折射率
(4)光从一种介质进入另一种介质时,折射角与入射角的大小关系不要一概而论,要视两种介质的折射率大小而定。
(5)当光从折射率小的介质斜射入折射率大的介质时,入射角大于折射角,当光从折射率大的介质斜射入折射率小的介质时,入射角小于折射角。
三、折射率
空气对光的传播影响很小,可以作为真空处理
由于光的折射,水中物体的位置看起来比实际位置要高些。
应用1:渔民叉鱼
渔民怎样才能叉到鱼?
四、生活中的折射现象
高
水
看到的气球在折射光线的反向延长线上.
空气
应用2:在水下看水面上的物体比实际位置高还是低?
四、生活中的折射现象
应用3:铅笔弯折之谜
空气
水
A
A
界面
四、生活中的折射现象
应用4:井中的青蛙看岸上的物体的位置偏向哪里?
偏向上方
井中的青蛙看井口的宽度是偏大还是偏小?
偏小
四、生活中的折射现象
SS′有大气,看到太阳更早没有大气,将迟一些看到太阳四、生活中的折射现象应用5:蒙气差现象
四、生活中的折射现象
1.常规思路
(1)根据题意画出正确的光路图.
(2)利用几何关系确定光路图中的边、角关系,要注意入射角、折射角均是与法线的夹角.
(3)利用折射定律、折射率公式列式求解.
解决光的折射问题的常规思路
2.视深问题
(1)视深是人眼看透明物质内部某物点时像点离界面的距离.在中学阶段,一般都是沿着界面的法线方向去观察,在计算时,由于入射角很小,折射角也很小,故有 ,这是在视深问题中经常用到的关系式.
(2)当沿竖直方向看水中物体时,“视深”是实际深度的倍,n是水的折射率.
解决光的折射问题的视深问题
课堂小结
光的
折射
折射率
光的折射:光从一种介质斜射入另一种介质时,传播方向发生改变的现象。
入射光线、法线处在同一平面内,折射光线与入射光线分别位于法线的两侧;入射角的正弦与折射角的正弦成正比,即:
光从真空射入某种介质发生折射时,入射角的正弦与折射角的正弦之比,叫做这种介质的绝对折射率,简称折射率。用符号 n 表示。
【典例1】如图所示是光线以相同的入射角从空气射入三种不同介质时的折射情况,则在三种介质中光的传播速度最小的是( )
A.介质甲 B.介质乙 C.介质丙 D.三种介质均一样
【正确答案】C
典例分析
【典例2】光在某种玻璃中的传播速度是 ,要使光由玻璃射入空气时折射光线与反射光线成90°,则入射光线与反射光线的夹角成( )
A.30° B.60° C.45° D.90°
【正确答案】B
典例分析
【典例3】物理社团的同学想测量一透明物体的折射率。如图所示,透明物体左右两侧紧靠遮光板,右下方压着一片小树叶,观察点距离透明物体左上边缘的高度为h、水平距离为2h时,恰好看到树叶。移走透明物体(小树叶和遮光板的位置不动),观察点水平向右移动,当水平移动距离 时,恰好又看到小树叶。则透明物体的折射率为( )
A. B. C. D.2
【正确答案】D
典例分析
【典例4】光线以60°的入射角从空气射入玻璃中,折射光线与反射光线恰好垂直。(真空中的光速c=3.0×108 m/s)
(1)画出折射光路图;
(2)求出玻璃的折射率和光在玻璃中的传播速度大小;
(3)当入射角变为45°时,折射角的正弦值是多大
(4)当入射角增大或减小时,玻璃的折射率是否变化
典例分析
【解析】 (1)由题意知入射角θ1=60°,反射角θ'=60°,折射角
θ2=180°-60°-90°=30°,光路图如图所示。
(4)折射率不会变化,折射率由介质和入射光线的频率决定,跟入射角的大小无关。
【典例5】如图所示,一束激光垂直于AC面照射到等边玻璃三棱镜的AB面上。已知AB面的反射光线与折射光线的夹角为90°。光在真空中的传播速度为c。求:(1)玻璃的折射率;
(2)激光在玻璃中传播的速度。
典例分析
【典例6】如图所示,一小孩站在宽6 m的河边,在他正对面的岸边有一距离河面高度为3 m的树,树的正下方河底有一块石头,小孩向河面看去,可同时看到树顶和石头两者的像,并发现两个像重合,若小孩的眼睛离河面高为1.5 m,河水的折射率为 ,试估算河水深度。
典例分析
【答案】 5.3 m
【解析】树顶反射和石头折射成像的光路图如图所示
