北师数学必修第一册第一章集合1.3集合的基本运算第2课时全集与补集(知识点+题型+自测题)(有答案)
文档属性
| 名称 | 北师数学必修第一册第一章集合1.3集合的基本运算第2课时全集与补集(知识点+题型+自测题)(有答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 175.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-07 00:00:00 | ||
图片预览




文档简介
集合
1.3集合的基本运算
第2课时 全集与补集
教学目标
1.能根据集合间的运算结果判断两个集合之间的关系.
2.能根据两个集合的运算结果求参数的取值范围.
知识点归类
知识点1 全集
(1)定义:在研究某些集合的时候,它们往往是某个给定集合的__子集__,这个给定的集合叫作全集.
(2)表示方法:常用符号U表示.
思考1:在集合运算问题中,全集一定是实数集吗?
提示:全集是一个相对性的概念,只包含研究问题中涉及的所有的元素,所以全集因问题的不同而异.
知识点2 补集
思考2:怎样理解补集?
提示:(1)补集是相对于全集而言的,一方面,若没有定义全集,则不存在补集的说法;另一方面,补集的元素逃不出全集的范围.
(2)补集既是集合之间的一种关系,也是集合之间的一种运算.在给定全集U的情况下,求集合A的补集的前提是A为全集U的子集,随着所选全集的不同,得到的补集也是不同的.
知识点3 补集的性质
对任何集合A,有A∪( UA)=__U__,A∩( UA)=__ __, U( UA)=__A__.
题型归类
题型一 补集的运算
例 1 (1)已知全集为U,集合A={1,3,5,7}, UA={2,4,6}, UB={1,4,6},则集合B=__{2,3,5,7}__.
(2)已知全集U={x|x≤5},集合A={x|-3≤x<5},则 UA=__{x|x<-3,或x=5}__.
[分析] (1)先结合条件,由补集的性质求出全集U,再由补集的定义求出集合B,也可借助Venn图求解.
(2)利用补集的定义,借助于数轴的直观作用求解.
[解析] (1)∵A={1,3,5,7}, UA={2,4,6},
∴U={1,2,3,4,5,6,7}.
又 UB={1,4,6},∴B={2,3,5,7}.
(2)将全集U和集合A分别表示在数轴上,如图所示.
由补集的定义可知 UA={x|x<-3,或x=5}.
[归纳提升] 求集合的补集的方法
1.定义法:当集合中的元素较少时,可利用定义直接求解.
2.数轴法:当集合中的元素连续且无限时,可借助数轴求解,此时需注意端点问题.
【对点练习】 (1)设全集U={x∈N|x≥2},集合A={x∈N|x2≥5},则 UA=( B )
A. B.{2}
C.{5} D.{2,5}
(2)已知全集U={x|1≤x≤5},A={x|1≤x<a},若 UA={x|2≤x≤5},则a=__2__.
[解析] (1)由题意知集合A={x∈N|x≥},则 UA={x∈N|2≤x<}={2},故选B.
(2)∵A∪( UA)=U,且A∩( UA)= ,
∴A={x|1≤x<2},∴a=2.
题型二 交集、并集、补集的综合运算
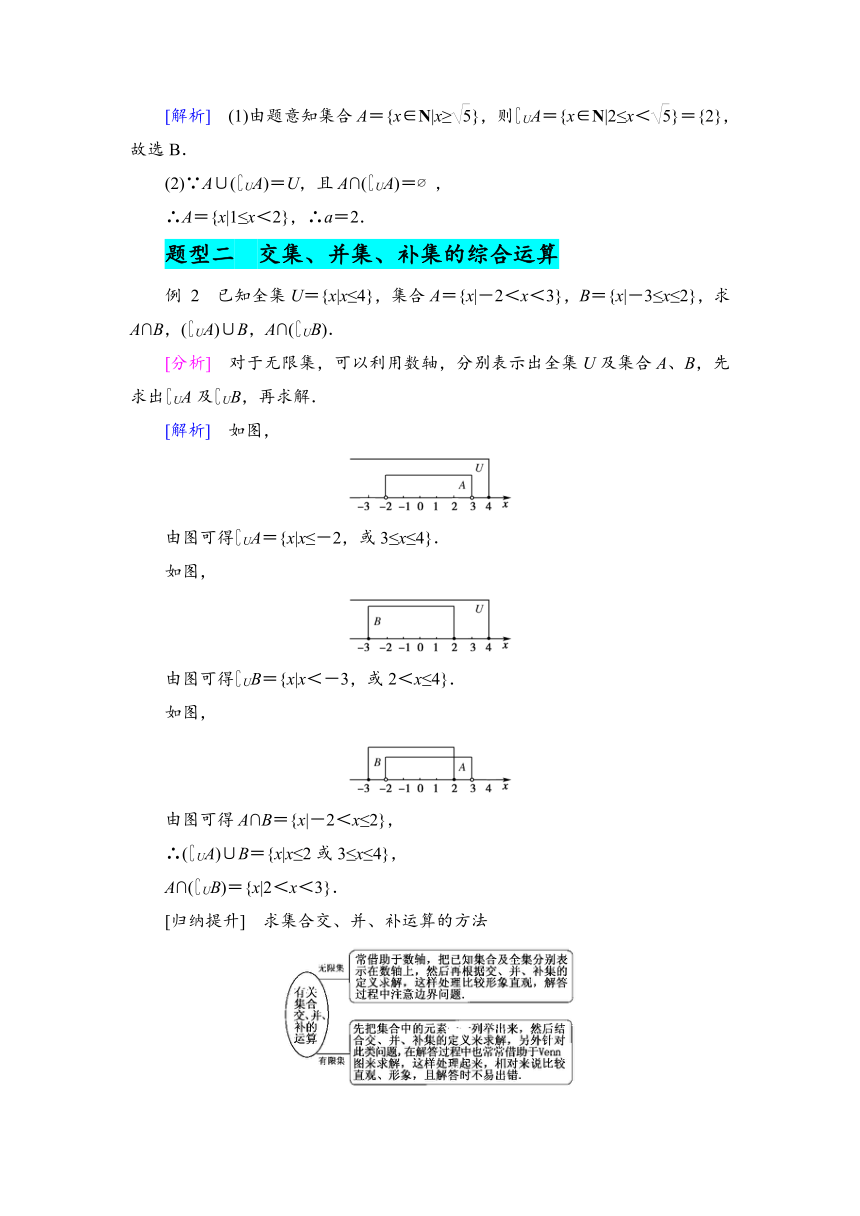
例 2 已知全集U={x|x≤4},集合A={x|-2<x<3},B={x|-3≤x≤2},求A∩B,( UA)∪B,A∩( UB).
[分析] 对于无限集,可以利用数轴,分别表示出全集U及集合A、B,先求出 UA及 UB,再求解.
[解析] 如图,
由图可得 UA={x|x≤-2,或3≤x≤4}.
如图,
由图可得 UB={x|x<-3,或2<x≤4}.
如图,
由图可得A∩B={x|-2<x≤2},
∴( UA)∪B={x|x≤2或3≤x≤4},
A∩( UB)={x|2<x<3}.
[归纳提升] 求集合交、并、补运算的方法
【对点练习】 (1)已知集合U={1,2,3,4},A={1,3},B={1,3,4},则A∪( UB)=__{1,2,3}__;
(2)设U=R,A={x|x>0},B={x|x>1},则A∩( UB)=( B )
A.{x|0≤x<1} B.{x|0<x≤1}
C.{x|x<0} D.{x|x>1}
[解析] (1) UB={2},A∪( UB)={1,2,3}.
(2)∵U=R,B={x|x>1},∴ UB={x|x≤1}.又A={x|x>0},∴A∩( UB)={x|0<x≤1}.
题型三 根据集合运算结果求参数的值或范围
例 3 已知全集U=R,集合A={x|x≤1或x≥3},集合B={x|k<x<2k+1},且( UA)∩B= ,求实数k的取值范围.
[分析] 求 UA,然后根据( UA)∩B= 分类讨论.
[解析] 因为全集U=R,集合A={x|x≤1或x≥3},
所以 UA={x|1<x<3},
因为集合B={x|k<x<2k+1},( UA)∩B= ,
所以分以下两种情况讨论:
(1)若B= ,则k≥2k+1,解得k≤-1;
(2)若B≠ ,则或解得k≥3或-1<k≤0.
由(1)(2)可知,实数k的取值范围是k≤0或k≥3.
[归纳提升] 由集合运算结果求参数的方法
(1)利用数轴分析.
当集合中元素个数无限时,可根据集合运算结果画数轴直观展示各集合之间的关系,通过分析数轴上有关点的位置关系列方程(或不等式)求参数的值(或范围).
【对点练习】 若集合A={x|ax2+3x+2=0}中至多有1个元素,则实数a的取值范围为____.
[解析] 假设集合A中含有2个元素,即ax2+3x+2=0有两个不相等的实数根,则解得a<且a≠0,则此时实数a的取值范围是.在全集U=R中,集合的补集是
.
所以满足题意的实数a的取值范围是.
A 组·基础自测
一、选择题
1.设全集U={1,2,3,4,5},集合A={1,2},则 UA等于( )
A.{1,2} B.{3,4,5}
C.{1,2,3,4,5} D.
2.已知A={x|x+1>0},B={-2,-1,0,1},则( RA)∩B等于( )
A.{-2,-1} B.{-2}
C.{-1,0,1} D.{0,1}
3.如图所示,U是全集,A,B是U的子集,则阴影部分所表示的集合是( )
A.A∩B B.A∪B
C.B∩( UA) D.A∩( UB)
4.已知集合U=(0,+∞), UA=(0,2),那么集合A=( )
A.(-∞,0]∪[2,+∞)B.(-∞,0)∪(2,+∞)
C.[2,+∞) D.(2,+∞)
5.设集合U={-1,1,2,3},M={x|x2+px+q=0},若 UM={-1,1},则实数p+q的值为( )
A.-1 B.-5
C.5 D.1
6.设全集U=R,集合A={x|x≤1,或x≥3},集合B={x|k<x<k+1,k∈R},且B∩( UA)≠ ,则( )
A.k<0或k>3 B.2<k<3
C.0<k<3 D.-1<k<3
二、填空题
7.设集合A={x|1<x<4},B={x|-1≤x≤3},则A∩( RB)=____.
8.有15人进入家电超市,其中有9人买了电视机,有7人买了电脑,两种均买的有3人,则这两种均没买的有____人.
三、解答题
9.已知全集U=R,A={x|-4≤x<2},B={x|-1<x≤3},P={x|x≤0或x≥},求A∩B,( UB)∪P,(A∩B)∩( UP).
10.已知集合U={1,2,3,4,5},若A∪B=U,A∩B= ,且A∩( UB)={1,2},试写出满足上述条件的集合A,B.
B 组·能力提升
一、选择题
1.设全集U={1,2,3,4,5},A={1,3,5},则 UA的所有非空子集的个数为( )
A.4 B.3
C.2 D.1
2.设P=(4,+∞),Q=(-2,2),则( )
A.P Q B.Q P
C.P RQ D.Q RP
3.设M、P是两个非空集合,定义M与P的差集为M-P={x|x∈M,且x P},则M-(M-P)等于( )
A.P B.M
C.M∩P D.M∪P
4.(多选题)已知集合U=R,集合A={x|1≤x≤3或4<x<6},集合B={x|2≤x<5},下列集合运算正确的是( )
A. UA={x|x<1或3<x<4或x>6}
B. UB={x|x<2或x≥5}
C.A∩( UB)={x|1≤x<2或5≤x<6}
D.( UA)∪B={x|x<1或2<x<5或x>6}
二、填空题
5.已知集合A={x|m-4<x<2m},B={x|-1<x<4},若A∩B=B,则实数m的取值范围为___.
6.设全集U={(x,y)|x∈R,y∈R},A=,B={(x,y)|y=x+1},则( UA)∩B=___.
三、解答题
7.设全集I={2,3,x2+2x-3},A={5}, IA={2,y},求实数x、y的值.
8.已知集合A={x|x2+ax+2b=0}和B={x|x2-ax+b=0},满足( UA)∩B={2},A∩( UB)={4},U=R,求实数a,b的值.
A 组·基础自测
一、选择题
1.设全集U={1,2,3,4,5},集合A={1,2},则 UA等于( B )
A.{1,2} B.{3,4,5}
C.{1,2,3,4,5} D.
[解析] ∵U={1,2,3,4,5},A={1,2},∴ UA={3,4,5}.
2.已知A={x|x+1>0},B={-2,-1,0,1},则( RA)∩B等于( A )
A.{-2,-1} B.{-2}
C.{-1,0,1} D.{0,1}
[解析] 因为集合A={x|x>-1},所以 RA={x|x≤-1},则( RA)∩B={x|x≤-1}∩{-2,-1,0,1}={-2,-1}.
3.如图所示,U是全集,A,B是U的子集,则阴影部分所表示的集合是( C )
A.A∩B B.A∪B
C.B∩( UA) D.A∩( UB)
[解析] 题图阴影部分表示由所有属于B且不属于A的元素组成的集合,故为B∩( UA).
4.已知集合U=(0,+∞), UA=(0,2),那么集合A=( C )
A.(-∞,0]∪[2,+∞)B.(-∞,0)∪(2,+∞)
C.[2,+∞) D.(2,+∞)
[解析] 利用数轴分析,可知A=[2,+∞).
5.设集合U={-1,1,2,3},M={x|x2+px+q=0},若 UM={-1,1},则实数p+q的值为( D )
A.-1 B.-5
C.5 D.1
[解析] 由已知可得M={2,3},
则2,3为方程x2+px+q=0的两根,
则p=-(2+3)=-5,
q=2×3=6,故p+q=-5+6=1.故选D.
6.设全集U=R,集合A={x|x≤1,或x≥3},集合B={x|k<x<k+1,k∈R},且B∩( UA)≠ ,则( C )
A.k<0或k>3 B.2<k<3
C.0<k<3 D.-1<k<3
[解析] UA={x|1<x<3},借助于数轴可得
∴0<k<3.
二、填空题
7.设集合A={x|1<x<4},B={x|-1≤x≤3},则A∩( RB)=__{x|3<x<4}__.
[解析] ∵B={x|-1≤x≤3},
则 RB={x|x<-1或x>3},
∴A∩( RB)={x|3<x<4}.
8.有15人进入家电超市,其中有9人买了电视机,有7人买了电脑,两种均买的有3人,则这两种均没买的有
__2__人.
[解析] 设这15人构成全集U,买电视机的9人构成集合A,买电脑的7人构成集合B,用Venn图表示,如图所示.
则两种均没买的有15-(9-3)-3-(7-3)=2(人).
三、解答题
9.已知全集U=R,A={x|-4≤x<2},B={x|-1<x≤3},P={x|x≤0或x≥},求A∩B,( UB)∪P,(A∩B)∩( UP).
[解析] 将集合A,B,P表示在数轴上,如图.
∵A={x|-4≤x<2},B={x|-1<x≤3},
∴A∩B={x|-1<x<2}.
∵ UB={x|x≤-1或x>3},
∴( UB)∪P=,
∴(A∩B)∩( UP)={x|-1<x<2}∩={x|0<x<2}.
10.已知集合U={1,2,3,4,5},若A∪B=U,A∩B= ,且A∩( UB)={1,2},试写出满足上述条件的集合A,B.
[解析] ∵A∪B=U,A∩B= ,
∴A= UB,又A∩( UB)={1,2},
∴A={1,2},∴B={3,4,5}.
B 组·能力提升
一、选择题
1.设全集U={1,2,3,4,5},A={1,3,5},则 UA的所有非空子集的个数为( B )
A.4 B.3
C.2 D.1
[解析] ∵ UA={2,4},∴非空子集有22-1=3个,故选B.
2.设P=(4,+∞),Q=(-2,2),则( D )
A.P Q B.Q P
C.P RQ D.Q RP
[解析] ∵Q=(-2,2),
而 RP=(-∞,4],
∴Q RP.
3.设M、P是两个非空集合,定义M与P的差集为M-P={x|x∈M,且x P},则M-(M-P)等于( C )
A.P B.M
C.M∩P D.M∪P
[解析] 当M∩P= 时,由于对任意x∈M都有x P,所以M-P=M,因此M-(M-P)=M-M= =M∩P;当M∩P≠ 时,作出Venn图如图所示,
则M-P表示在M中但不在P中的元素构成的集合,因而M-(M-P)表示由在M中但不在M-P中的元素构成的集合.由于M-P中的元素都不在P中,所以M-(M-P)中的元素都在P中,所以M-(M-P)中的元素都在M∩P中,反过来M∩P中的元素也符合M-(M-P)的定义,因此M-(M-P)=M∩P,故选C.
4.(多选题)已知集合U=R,集合A={x|1≤x≤3或4<x<6},集合B={x|2≤x<5},下列集合运算正确的是( BC )
A. UA={x|x<1或3<x<4或x>6}
B. UB={x|x<2或x≥5}
C.A∩( UB)={x|1≤x<2或5≤x<6}
D.( UA)∪B={x|x<1或2<x<5或x>6}
[解析] 由 UA={x|x<1或3<x≤4或x≥6}知选项A错误;
由 UB={x|x<2或x≥5}知选项B正确;
由A∩( UB)={x|1≤x≤3或4<x<6}∩{x|x<2或x≥5}={x|1≤x<2或5≤x<6}知选项C正确;
由( UA)∪B={x|x<1或3<x≤4或x≥6}∪{x|2≤x<5}={x|x<1或2≤x<5或x≥6}知选项D错误.
二、填空题
5.已知集合A={x|m-4<x<2m},B={x|-1<x<4},若A∩B=B,则实数m的取值范围为__{m|2≤m≤3}__.
[解析] ∵A∩B=B,∴B A,∵A={x|m-4<x<2m},B={x|-1<x<4},
∴解得2≤m≤3,
即实数m的取值范围为{m|2≤m≤3}.
6.设全集U={(x,y)|x∈R,y∈R},A=,B={(x,y)|y=x+1},则( UA)∩B=__{(2,3)}__.
[解析] ∵A=={(x,y)|y=x+1,x≠2},∴ UA={(x,y)|y≠x+1}∪{(2,3)}.
又B={(x,y)|y=x+1},
∴( UA)∩B={(2,3)}.
三、解答题
7.设全集I={2,3,x2+2x-3},A={5}, IA={2,y},求实数x、y的值.
[解析] 因为A={5}, IA={2,y}.
所以I={2,5,y},
又I={2,3,x2+2x-3},
所以,
所以或.
故x=2,y=3或x=-4,y=3.
8.已知集合A={x|x2+ax+2b=0}和B={x|x2-ax+b=0},满足( UA)∩B={2},A∩( UB)={4},U=R,求实数a,b的值.
[解析] ∵( UA)∩B={2},∴2∈B,
∴4-2a+b=0. ①
又∵A∩( UB)={4},∴4∈A,
∴16+4a+2b=0. ②
联立①②,得解得
经检验,符合题意:∴a=-1,b=-6.
1.3集合的基本运算
第2课时 全集与补集
教学目标
1.能根据集合间的运算结果判断两个集合之间的关系.
2.能根据两个集合的运算结果求参数的取值范围.
知识点归类
知识点1 全集
(1)定义:在研究某些集合的时候,它们往往是某个给定集合的__子集__,这个给定的集合叫作全集.
(2)表示方法:常用符号U表示.
思考1:在集合运算问题中,全集一定是实数集吗?
提示:全集是一个相对性的概念,只包含研究问题中涉及的所有的元素,所以全集因问题的不同而异.
知识点2 补集
思考2:怎样理解补集?
提示:(1)补集是相对于全集而言的,一方面,若没有定义全集,则不存在补集的说法;另一方面,补集的元素逃不出全集的范围.
(2)补集既是集合之间的一种关系,也是集合之间的一种运算.在给定全集U的情况下,求集合A的补集的前提是A为全集U的子集,随着所选全集的不同,得到的补集也是不同的.
知识点3 补集的性质
对任何集合A,有A∪( UA)=__U__,A∩( UA)=__ __, U( UA)=__A__.
题型归类
题型一 补集的运算
例 1 (1)已知全集为U,集合A={1,3,5,7}, UA={2,4,6}, UB={1,4,6},则集合B=__{2,3,5,7}__.
(2)已知全集U={x|x≤5},集合A={x|-3≤x<5},则 UA=__{x|x<-3,或x=5}__.
[分析] (1)先结合条件,由补集的性质求出全集U,再由补集的定义求出集合B,也可借助Venn图求解.
(2)利用补集的定义,借助于数轴的直观作用求解.
[解析] (1)∵A={1,3,5,7}, UA={2,4,6},
∴U={1,2,3,4,5,6,7}.
又 UB={1,4,6},∴B={2,3,5,7}.
(2)将全集U和集合A分别表示在数轴上,如图所示.
由补集的定义可知 UA={x|x<-3,或x=5}.
[归纳提升] 求集合的补集的方法
1.定义法:当集合中的元素较少时,可利用定义直接求解.
2.数轴法:当集合中的元素连续且无限时,可借助数轴求解,此时需注意端点问题.
【对点练习】 (1)设全集U={x∈N|x≥2},集合A={x∈N|x2≥5},则 UA=( B )
A. B.{2}
C.{5} D.{2,5}
(2)已知全集U={x|1≤x≤5},A={x|1≤x<a},若 UA={x|2≤x≤5},则a=__2__.
[解析] (1)由题意知集合A={x∈N|x≥},则 UA={x∈N|2≤x<}={2},故选B.
(2)∵A∪( UA)=U,且A∩( UA)= ,
∴A={x|1≤x<2},∴a=2.
题型二 交集、并集、补集的综合运算
例 2 已知全集U={x|x≤4},集合A={x|-2<x<3},B={x|-3≤x≤2},求A∩B,( UA)∪B,A∩( UB).
[分析] 对于无限集,可以利用数轴,分别表示出全集U及集合A、B,先求出 UA及 UB,再求解.
[解析] 如图,
由图可得 UA={x|x≤-2,或3≤x≤4}.
如图,
由图可得 UB={x|x<-3,或2<x≤4}.
如图,
由图可得A∩B={x|-2<x≤2},
∴( UA)∪B={x|x≤2或3≤x≤4},
A∩( UB)={x|2<x<3}.
[归纳提升] 求集合交、并、补运算的方法
【对点练习】 (1)已知集合U={1,2,3,4},A={1,3},B={1,3,4},则A∪( UB)=__{1,2,3}__;
(2)设U=R,A={x|x>0},B={x|x>1},则A∩( UB)=( B )
A.{x|0≤x<1} B.{x|0<x≤1}
C.{x|x<0} D.{x|x>1}
[解析] (1) UB={2},A∪( UB)={1,2,3}.
(2)∵U=R,B={x|x>1},∴ UB={x|x≤1}.又A={x|x>0},∴A∩( UB)={x|0<x≤1}.
题型三 根据集合运算结果求参数的值或范围
例 3 已知全集U=R,集合A={x|x≤1或x≥3},集合B={x|k<x<2k+1},且( UA)∩B= ,求实数k的取值范围.
[分析] 求 UA,然后根据( UA)∩B= 分类讨论.
[解析] 因为全集U=R,集合A={x|x≤1或x≥3},
所以 UA={x|1<x<3},
因为集合B={x|k<x<2k+1},( UA)∩B= ,
所以分以下两种情况讨论:
(1)若B= ,则k≥2k+1,解得k≤-1;
(2)若B≠ ,则或解得k≥3或-1<k≤0.
由(1)(2)可知,实数k的取值范围是k≤0或k≥3.
[归纳提升] 由集合运算结果求参数的方法
(1)利用数轴分析.
当集合中元素个数无限时,可根据集合运算结果画数轴直观展示各集合之间的关系,通过分析数轴上有关点的位置关系列方程(或不等式)求参数的值(或范围).
【对点练习】 若集合A={x|ax2+3x+2=0}中至多有1个元素,则实数a的取值范围为____.
[解析] 假设集合A中含有2个元素,即ax2+3x+2=0有两个不相等的实数根,则解得a<且a≠0,则此时实数a的取值范围是.在全集U=R中,集合的补集是
.
所以满足题意的实数a的取值范围是.
A 组·基础自测
一、选择题
1.设全集U={1,2,3,4,5},集合A={1,2},则 UA等于( )
A.{1,2} B.{3,4,5}
C.{1,2,3,4,5} D.
2.已知A={x|x+1>0},B={-2,-1,0,1},则( RA)∩B等于( )
A.{-2,-1} B.{-2}
C.{-1,0,1} D.{0,1}
3.如图所示,U是全集,A,B是U的子集,则阴影部分所表示的集合是( )
A.A∩B B.A∪B
C.B∩( UA) D.A∩( UB)
4.已知集合U=(0,+∞), UA=(0,2),那么集合A=( )
A.(-∞,0]∪[2,+∞)B.(-∞,0)∪(2,+∞)
C.[2,+∞) D.(2,+∞)
5.设集合U={-1,1,2,3},M={x|x2+px+q=0},若 UM={-1,1},则实数p+q的值为( )
A.-1 B.-5
C.5 D.1
6.设全集U=R,集合A={x|x≤1,或x≥3},集合B={x|k<x<k+1,k∈R},且B∩( UA)≠ ,则( )
A.k<0或k>3 B.2<k<3
C.0<k<3 D.-1<k<3
二、填空题
7.设集合A={x|1<x<4},B={x|-1≤x≤3},则A∩( RB)=____.
8.有15人进入家电超市,其中有9人买了电视机,有7人买了电脑,两种均买的有3人,则这两种均没买的有____人.
三、解答题
9.已知全集U=R,A={x|-4≤x<2},B={x|-1<x≤3},P={x|x≤0或x≥},求A∩B,( UB)∪P,(A∩B)∩( UP).
10.已知集合U={1,2,3,4,5},若A∪B=U,A∩B= ,且A∩( UB)={1,2},试写出满足上述条件的集合A,B.
B 组·能力提升
一、选择题
1.设全集U={1,2,3,4,5},A={1,3,5},则 UA的所有非空子集的个数为( )
A.4 B.3
C.2 D.1
2.设P=(4,+∞),Q=(-2,2),则( )
A.P Q B.Q P
C.P RQ D.Q RP
3.设M、P是两个非空集合,定义M与P的差集为M-P={x|x∈M,且x P},则M-(M-P)等于( )
A.P B.M
C.M∩P D.M∪P
4.(多选题)已知集合U=R,集合A={x|1≤x≤3或4<x<6},集合B={x|2≤x<5},下列集合运算正确的是( )
A. UA={x|x<1或3<x<4或x>6}
B. UB={x|x<2或x≥5}
C.A∩( UB)={x|1≤x<2或5≤x<6}
D.( UA)∪B={x|x<1或2<x<5或x>6}
二、填空题
5.已知集合A={x|m-4<x<2m},B={x|-1<x<4},若A∩B=B,则实数m的取值范围为___.
6.设全集U={(x,y)|x∈R,y∈R},A=,B={(x,y)|y=x+1},则( UA)∩B=___.
三、解答题
7.设全集I={2,3,x2+2x-3},A={5}, IA={2,y},求实数x、y的值.
8.已知集合A={x|x2+ax+2b=0}和B={x|x2-ax+b=0},满足( UA)∩B={2},A∩( UB)={4},U=R,求实数a,b的值.
A 组·基础自测
一、选择题
1.设全集U={1,2,3,4,5},集合A={1,2},则 UA等于( B )
A.{1,2} B.{3,4,5}
C.{1,2,3,4,5} D.
[解析] ∵U={1,2,3,4,5},A={1,2},∴ UA={3,4,5}.
2.已知A={x|x+1>0},B={-2,-1,0,1},则( RA)∩B等于( A )
A.{-2,-1} B.{-2}
C.{-1,0,1} D.{0,1}
[解析] 因为集合A={x|x>-1},所以 RA={x|x≤-1},则( RA)∩B={x|x≤-1}∩{-2,-1,0,1}={-2,-1}.
3.如图所示,U是全集,A,B是U的子集,则阴影部分所表示的集合是( C )
A.A∩B B.A∪B
C.B∩( UA) D.A∩( UB)
[解析] 题图阴影部分表示由所有属于B且不属于A的元素组成的集合,故为B∩( UA).
4.已知集合U=(0,+∞), UA=(0,2),那么集合A=( C )
A.(-∞,0]∪[2,+∞)B.(-∞,0)∪(2,+∞)
C.[2,+∞) D.(2,+∞)
[解析] 利用数轴分析,可知A=[2,+∞).
5.设集合U={-1,1,2,3},M={x|x2+px+q=0},若 UM={-1,1},则实数p+q的值为( D )
A.-1 B.-5
C.5 D.1
[解析] 由已知可得M={2,3},
则2,3为方程x2+px+q=0的两根,
则p=-(2+3)=-5,
q=2×3=6,故p+q=-5+6=1.故选D.
6.设全集U=R,集合A={x|x≤1,或x≥3},集合B={x|k<x<k+1,k∈R},且B∩( UA)≠ ,则( C )
A.k<0或k>3 B.2<k<3
C.0<k<3 D.-1<k<3
[解析] UA={x|1<x<3},借助于数轴可得
∴0<k<3.
二、填空题
7.设集合A={x|1<x<4},B={x|-1≤x≤3},则A∩( RB)=__{x|3<x<4}__.
[解析] ∵B={x|-1≤x≤3},
则 RB={x|x<-1或x>3},
∴A∩( RB)={x|3<x<4}.
8.有15人进入家电超市,其中有9人买了电视机,有7人买了电脑,两种均买的有3人,则这两种均没买的有
__2__人.
[解析] 设这15人构成全集U,买电视机的9人构成集合A,买电脑的7人构成集合B,用Venn图表示,如图所示.
则两种均没买的有15-(9-3)-3-(7-3)=2(人).
三、解答题
9.已知全集U=R,A={x|-4≤x<2},B={x|-1<x≤3},P={x|x≤0或x≥},求A∩B,( UB)∪P,(A∩B)∩( UP).
[解析] 将集合A,B,P表示在数轴上,如图.
∵A={x|-4≤x<2},B={x|-1<x≤3},
∴A∩B={x|-1<x<2}.
∵ UB={x|x≤-1或x>3},
∴( UB)∪P=,
∴(A∩B)∩( UP)={x|-1<x<2}∩={x|0<x<2}.
10.已知集合U={1,2,3,4,5},若A∪B=U,A∩B= ,且A∩( UB)={1,2},试写出满足上述条件的集合A,B.
[解析] ∵A∪B=U,A∩B= ,
∴A= UB,又A∩( UB)={1,2},
∴A={1,2},∴B={3,4,5}.
B 组·能力提升
一、选择题
1.设全集U={1,2,3,4,5},A={1,3,5},则 UA的所有非空子集的个数为( B )
A.4 B.3
C.2 D.1
[解析] ∵ UA={2,4},∴非空子集有22-1=3个,故选B.
2.设P=(4,+∞),Q=(-2,2),则( D )
A.P Q B.Q P
C.P RQ D.Q RP
[解析] ∵Q=(-2,2),
而 RP=(-∞,4],
∴Q RP.
3.设M、P是两个非空集合,定义M与P的差集为M-P={x|x∈M,且x P},则M-(M-P)等于( C )
A.P B.M
C.M∩P D.M∪P
[解析] 当M∩P= 时,由于对任意x∈M都有x P,所以M-P=M,因此M-(M-P)=M-M= =M∩P;当M∩P≠ 时,作出Venn图如图所示,
则M-P表示在M中但不在P中的元素构成的集合,因而M-(M-P)表示由在M中但不在M-P中的元素构成的集合.由于M-P中的元素都不在P中,所以M-(M-P)中的元素都在P中,所以M-(M-P)中的元素都在M∩P中,反过来M∩P中的元素也符合M-(M-P)的定义,因此M-(M-P)=M∩P,故选C.
4.(多选题)已知集合U=R,集合A={x|1≤x≤3或4<x<6},集合B={x|2≤x<5},下列集合运算正确的是( BC )
A. UA={x|x<1或3<x<4或x>6}
B. UB={x|x<2或x≥5}
C.A∩( UB)={x|1≤x<2或5≤x<6}
D.( UA)∪B={x|x<1或2<x<5或x>6}
[解析] 由 UA={x|x<1或3<x≤4或x≥6}知选项A错误;
由 UB={x|x<2或x≥5}知选项B正确;
由A∩( UB)={x|1≤x≤3或4<x<6}∩{x|x<2或x≥5}={x|1≤x<2或5≤x<6}知选项C正确;
由( UA)∪B={x|x<1或3<x≤4或x≥6}∪{x|2≤x<5}={x|x<1或2≤x<5或x≥6}知选项D错误.
二、填空题
5.已知集合A={x|m-4<x<2m},B={x|-1<x<4},若A∩B=B,则实数m的取值范围为__{m|2≤m≤3}__.
[解析] ∵A∩B=B,∴B A,∵A={x|m-4<x<2m},B={x|-1<x<4},
∴解得2≤m≤3,
即实数m的取值范围为{m|2≤m≤3}.
6.设全集U={(x,y)|x∈R,y∈R},A=,B={(x,y)|y=x+1},则( UA)∩B=__{(2,3)}__.
[解析] ∵A=={(x,y)|y=x+1,x≠2},∴ UA={(x,y)|y≠x+1}∪{(2,3)}.
又B={(x,y)|y=x+1},
∴( UA)∩B={(2,3)}.
三、解答题
7.设全集I={2,3,x2+2x-3},A={5}, IA={2,y},求实数x、y的值.
[解析] 因为A={5}, IA={2,y}.
所以I={2,5,y},
又I={2,3,x2+2x-3},
所以,
所以或.
故x=2,y=3或x=-4,y=3.
8.已知集合A={x|x2+ax+2b=0}和B={x|x2-ax+b=0},满足( UA)∩B={2},A∩( UB)={4},U=R,求实数a,b的值.
[解析] ∵( UA)∩B={2},∴2∈B,
∴4-2a+b=0. ①
又∵A∩( UB)={4},∴4∈A,
∴16+4a+2b=0. ②
联立①②,得解得
经检验,符合题意:∴a=-1,b=-6.
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
