2.1代数式 第4课时 代数式的值 课件(共24张PPT) 沪科版七年级数学上册
文档属性
| 名称 | 2.1代数式 第4课时 代数式的值 课件(共24张PPT) 沪科版七年级数学上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-09 21:01:07 | ||
图片预览








文档简介
(共24张PPT)
第2章 整式加减
沪科版七年级数学上册
2.1 代数式
第4课时 代 数 式 的 值
根据代数式求值推断代数式所反映的规律
学 习 目 标
了解代数式的值的意义,会计算代数式的值.
认识两个数量之间的对应关系,在实际问题中列出代数式,解决简单的实际问题
2
1
3
一项调查研究显示:一个10—50岁的人,每天所需要的睡眠时间t h与他的年龄n岁之间的关系为:
例如,数学老师我今年33岁,那么我的每天所需要的睡眠时间为:
t=
算一算,你每天所需要的睡眠时间?
=7.7(h)
即约7小时42分钟。
新知导入
游戏方法:
活动:请四个同学来做一个传数的游戏
新知讲解
请第一个同学任意报一个数给第二个 同学,
第二个同学把这个数加1传给第三个同学,
第三个同学再把听到的数平方后传给第四个同学,
第四个同学把听到的数减去1报出答案。
问题一:若一个同学报给第二个同学的数是5,而第四个同学报出的答案是35。其结果对吗?
问题二:若第一个同学报给第二个同学的数是x,
则第二个同学报给第三个同学的数是_________,
第三个同学报给第四个同学的数是__________,
第四个同学报出的答案是______________.
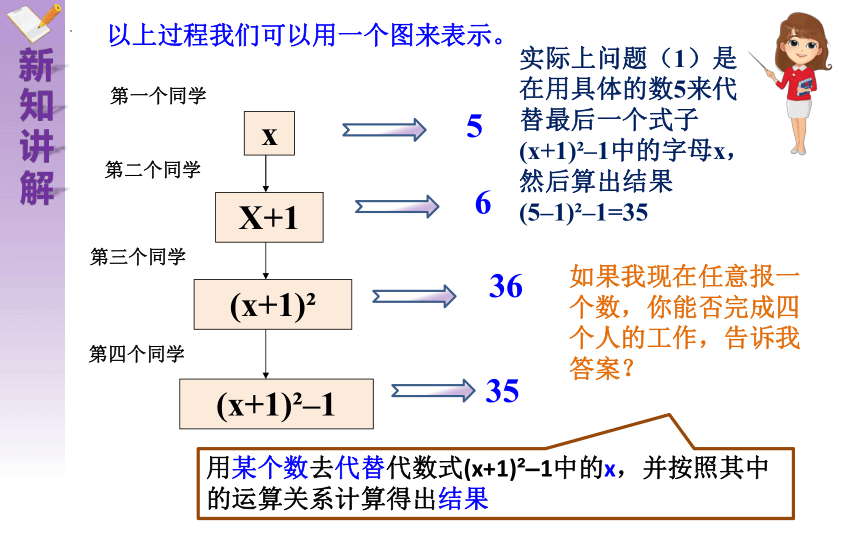
以上过程我们可以用一个图来表示。
5
6
36
35
x
X+1
(x+1)
(x+1) –1
实际上问题(1)是在用具体的数5来代替最后一个式子(x+1) –1中的字母x,然后算出结果(5–1) –1=35
如果我现在任意报一个数,你能否完成四个人的工作,告诉我答案?
新知讲解
第一个同学
第四个同学
第三个同学
第二个同学
用某个数去代替代数式(x+1) –1中的x,并按照其中的运算关系计算得出结果
代数式的值
新知讲解
用数值代替代数式里的字母,按照代数式中运算关系计算得出的结果,叫做代数式的值。
注意:
代数式中的字母在取值时必须保证在取值后代数式有意义
例1 当 x = -3,y = 2 时,求下列代数式的值:
解:
当 x = -3,y = 2 时
新知讲解
步骤
1.写出字母的值,用“当……时”写出来。
2.代入:在代入时只是将相应的字母换成数值,其他性质符号和运算符号不改变;
3.计算:按照运算顺序进行计算。
新知讲解
求代数式的值的步骤
在代数式中原来省略的乘号代入数值后要还原成“ × ”号
代入负数数值时要加上括号,代入乘方运算时,底数是负数或分数时也要加上括号
1、先代入后计算,代入步骤必不可少。
2、在将数字代入字母过程中,有时要适当地加入运算符号或括号
注意
例1 求下列各题
(1)当x=-3时,求 的值;
(2)当a=0.5,b=-2时,求 的值.
解:(1)当x=-3时,
(2)当a=0.5,b=-2时,
求代数式的值
典例精析
(1) 写出条件:当……时
(2) 抄写代数式
(3) 代入数值
(4) 计算
整体代入法求代数式的值
例2 已知x+y=5, xy=2, 求代数式(x+y)2-5xy 的值.
=25-10
解:∵x+y=5, xy=2,
原式=52-5×2
=15
典例精析
相同的代数式可以看作一个字母——整体代入
解析:
题中 x,y 的值没单独给出,可将 x+y,xy看做整体,代入到所求代数式中.
1、已知 x - 2y = 3,则代数式 6 - 2(x - 2y) 的值 为____.
随堂练习
0
2. 若已知 如何求 的值呢?
提示:3x2 - 12x = 3(x2 - 4x)
解:3x2 - 12x - 10 = 3(x2 - 4x) - 10 = 3×3 - 10 = - 1.
例3、某农场购买了一台新型拖拉机用来耕地.为了测试耕地时的耗油量,用它试耕了三块地,其面积分别为0.4公顷,0.6公顷和1公顷.油量表的指针变化情况如图所示(油表中的一个大格表示10升油).
典例精析
(1)根据油量表指针的变化,估算耕地0.4公顷,0.6公顷,1公顷的耗油量(升),与同学交流,并将结果填入表中.
耕地面积/公顷 0.4 0.6 1
耗油量/升
耕地面积/公顷 0.4 0.6 1
耗油量/升 10 15 25
典例精析
(2)如果设耕地a (公顷)耗油量为b(升),列代数式表示a和b之间的关系.
解:每耕1公顷地,耗油量为25升
b=25a
(3)根据所列的关系式,求解下列问题:
①耕地面积为0.5公顷,2公顷时,耗油量分别是多少?
②如果两次耕地耗油量分别是12升和40升,那么所耕地的面积分别是多少公顷?
当a=0.5公顷时
b=25×0.5=12.5(升)
当a=2公顷时
b=25×2=50(升)
解:
当b=12升时
a = 12÷25 = 4.8(公顷)
解:
1. 当x=﹣1时,代数式3x+1的值是( )
A.﹣1 B.﹣2
C.4 D.﹣4
解析:把x=﹣1代入代数式中,得
3x+1=﹣3+1=﹣2.
B
链接中考
解析:观察图形知,第一个图形有3个正方形,第二个有5=3+2×1个,第三个图形有7=3+2×2个……
故第⑥个图中的黑色正方形纸片有3+2×5=13(张).
2. 下列图形都是由同样大小的黑色正方形纸片组成的,其中第①个图中有3张黑色正方形纸片,第②个图中有5张黑色正方形纸片,第③个图中有7张黑色正方形纸片……按此规律排列下去,第⑥个图中黑色正方形纸片的张数为( ).
A.11 B.13
C.15 D.17
B
链接中考
1. 当 a = 2,b = 1,c = 3 时,代数式 c - (c - a)(c - b) 的值是( )
A. 1 B. 2 C. 3 D. 4
A
3. 已知 a + b = 5,ab = 6,则 ab - (a + b) =___.
2. 当 a = - 2,b = - 1 时,1 - |b - a| =___.
1
0
4. 如果 2a + 3b = 5,那么 4a + 6b - 7 =__.
3
课堂检测
5、填图:
n
3n2-2n+4
3
0
-4
课堂检测
(1)一个旅游团有成人x人、学生y人,那么该旅游团应付多少门票费?
(2)如果该旅游团有37个成人、15个学生,那么他们应付多少门票费?
6、某公园的门票价格是:成人10元/张;学生5元/张.
解:(1)该旅游团应付的门票费是(10x+5y)元.
(2)把x=37,y=15代入代数式,得
10x+5y =10×37+5×15 =445.
因此,他们应付445元门票费.
课堂检测
拓展提升
1.已知a、b为两个不相等的有理数,根据流程图中的程序,若输入的a值是10,输出的c值为20,则输入的b值是( )
A.15 B.10 C.0 D.20
C
课堂检测
拓展提升
解:a>b时,根据题意得:c=m+a+b=2(a+b)=20,即a+b=10,
将a=10代入得:b=0,
经检验符合题意,
a<b时,m=b-a,c=b-a+a+b=2b=20,
解得:b=10,
经检验a=b,不合题意,舍去,
则b的值为0.
课堂检测
课堂检测
拓展提升
2、如图,文化广场上摆了一些桌子,若并排摆n张桌子,可同时容纳多少人?当n=20时,可同时容纳多少人?
解: , ,
1
1
2
n
1
2
……
……
(1)
(2)
(n)
当 时,可同时容纳:
(人).
3、一辆卡车在行驶时平均每小时耗油8升,行驶前油箱中有油80升.
⑴用代数式表示行驶x小时后,油箱中的剩余油量
Q=______;
⑵计算行驶2小时,5小时,8小时后,油箱中的剩余油量。
⑶这里,能求x=12小时时剩余油量Q的值吗?
80—8x
拓展提升
课堂检测
当x=2小时
(2)解:
Q=80- 8x
=80-8×2
=64(升)
当x=5小时
Q=80- 8x
=80-8×5
=40(升)
当x=8小时
Q=80- 8x
=80-8×8
=16(升)
(3)解:
当x=12小时
Q=80- 8x=80-8×12
=-16(升)<0
没有实际意义,不能求出剩余油量
本题中的x不能取负数和大于10的值
代数式里的字母虽然可以取不同的数值,但是这些数值不能使代数式和它表示的实际问题失去意义。
代数式的值
概念
应用
用数值代替代数式中的 ,
按照代数式中的 关系计算得出的结果叫做代数式的值
运算
字母
直接代入求值
列代数式求值
整体代入求值
步骤
1. 代入
2. 计算
课堂总结
第2章 整式加减
沪科版七年级数学上册
2.1 代数式
第4课时 代 数 式 的 值
根据代数式求值推断代数式所反映的规律
学 习 目 标
了解代数式的值的意义,会计算代数式的值.
认识两个数量之间的对应关系,在实际问题中列出代数式,解决简单的实际问题
2
1
3
一项调查研究显示:一个10—50岁的人,每天所需要的睡眠时间t h与他的年龄n岁之间的关系为:
例如,数学老师我今年33岁,那么我的每天所需要的睡眠时间为:
t=
算一算,你每天所需要的睡眠时间?
=7.7(h)
即约7小时42分钟。
新知导入
游戏方法:
活动:请四个同学来做一个传数的游戏
新知讲解
请第一个同学任意报一个数给第二个 同学,
第二个同学把这个数加1传给第三个同学,
第三个同学再把听到的数平方后传给第四个同学,
第四个同学把听到的数减去1报出答案。
问题一:若一个同学报给第二个同学的数是5,而第四个同学报出的答案是35。其结果对吗?
问题二:若第一个同学报给第二个同学的数是x,
则第二个同学报给第三个同学的数是_________,
第三个同学报给第四个同学的数是__________,
第四个同学报出的答案是______________.
以上过程我们可以用一个图来表示。
5
6
36
35
x
X+1
(x+1)
(x+1) –1
实际上问题(1)是在用具体的数5来代替最后一个式子(x+1) –1中的字母x,然后算出结果(5–1) –1=35
如果我现在任意报一个数,你能否完成四个人的工作,告诉我答案?
新知讲解
第一个同学
第四个同学
第三个同学
第二个同学
用某个数去代替代数式(x+1) –1中的x,并按照其中的运算关系计算得出结果
代数式的值
新知讲解
用数值代替代数式里的字母,按照代数式中运算关系计算得出的结果,叫做代数式的值。
注意:
代数式中的字母在取值时必须保证在取值后代数式有意义
例1 当 x = -3,y = 2 时,求下列代数式的值:
解:
当 x = -3,y = 2 时
新知讲解
步骤
1.写出字母的值,用“当……时”写出来。
2.代入:在代入时只是将相应的字母换成数值,其他性质符号和运算符号不改变;
3.计算:按照运算顺序进行计算。
新知讲解
求代数式的值的步骤
在代数式中原来省略的乘号代入数值后要还原成“ × ”号
代入负数数值时要加上括号,代入乘方运算时,底数是负数或分数时也要加上括号
1、先代入后计算,代入步骤必不可少。
2、在将数字代入字母过程中,有时要适当地加入运算符号或括号
注意
例1 求下列各题
(1)当x=-3时,求 的值;
(2)当a=0.5,b=-2时,求 的值.
解:(1)当x=-3时,
(2)当a=0.5,b=-2时,
求代数式的值
典例精析
(1) 写出条件:当……时
(2) 抄写代数式
(3) 代入数值
(4) 计算
整体代入法求代数式的值
例2 已知x+y=5, xy=2, 求代数式(x+y)2-5xy 的值.
=25-10
解:∵x+y=5, xy=2,
原式=52-5×2
=15
典例精析
相同的代数式可以看作一个字母——整体代入
解析:
题中 x,y 的值没单独给出,可将 x+y,xy看做整体,代入到所求代数式中.
1、已知 x - 2y = 3,则代数式 6 - 2(x - 2y) 的值 为____.
随堂练习
0
2. 若已知 如何求 的值呢?
提示:3x2 - 12x = 3(x2 - 4x)
解:3x2 - 12x - 10 = 3(x2 - 4x) - 10 = 3×3 - 10 = - 1.
例3、某农场购买了一台新型拖拉机用来耕地.为了测试耕地时的耗油量,用它试耕了三块地,其面积分别为0.4公顷,0.6公顷和1公顷.油量表的指针变化情况如图所示(油表中的一个大格表示10升油).
典例精析
(1)根据油量表指针的变化,估算耕地0.4公顷,0.6公顷,1公顷的耗油量(升),与同学交流,并将结果填入表中.
耕地面积/公顷 0.4 0.6 1
耗油量/升
耕地面积/公顷 0.4 0.6 1
耗油量/升 10 15 25
典例精析
(2)如果设耕地a (公顷)耗油量为b(升),列代数式表示a和b之间的关系.
解:每耕1公顷地,耗油量为25升
b=25a
(3)根据所列的关系式,求解下列问题:
①耕地面积为0.5公顷,2公顷时,耗油量分别是多少?
②如果两次耕地耗油量分别是12升和40升,那么所耕地的面积分别是多少公顷?
当a=0.5公顷时
b=25×0.5=12.5(升)
当a=2公顷时
b=25×2=50(升)
解:
当b=12升时
a = 12÷25 = 4.8(公顷)
解:
1. 当x=﹣1时,代数式3x+1的值是( )
A.﹣1 B.﹣2
C.4 D.﹣4
解析:把x=﹣1代入代数式中,得
3x+1=﹣3+1=﹣2.
B
链接中考
解析:观察图形知,第一个图形有3个正方形,第二个有5=3+2×1个,第三个图形有7=3+2×2个……
故第⑥个图中的黑色正方形纸片有3+2×5=13(张).
2. 下列图形都是由同样大小的黑色正方形纸片组成的,其中第①个图中有3张黑色正方形纸片,第②个图中有5张黑色正方形纸片,第③个图中有7张黑色正方形纸片……按此规律排列下去,第⑥个图中黑色正方形纸片的张数为( ).
A.11 B.13
C.15 D.17
B
链接中考
1. 当 a = 2,b = 1,c = 3 时,代数式 c - (c - a)(c - b) 的值是( )
A. 1 B. 2 C. 3 D. 4
A
3. 已知 a + b = 5,ab = 6,则 ab - (a + b) =___.
2. 当 a = - 2,b = - 1 时,1 - |b - a| =___.
1
0
4. 如果 2a + 3b = 5,那么 4a + 6b - 7 =__.
3
课堂检测
5、填图:
n
3n2-2n+4
3
0
-4
课堂检测
(1)一个旅游团有成人x人、学生y人,那么该旅游团应付多少门票费?
(2)如果该旅游团有37个成人、15个学生,那么他们应付多少门票费?
6、某公园的门票价格是:成人10元/张;学生5元/张.
解:(1)该旅游团应付的门票费是(10x+5y)元.
(2)把x=37,y=15代入代数式,得
10x+5y =10×37+5×15 =445.
因此,他们应付445元门票费.
课堂检测
拓展提升
1.已知a、b为两个不相等的有理数,根据流程图中的程序,若输入的a值是10,输出的c值为20,则输入的b值是( )
A.15 B.10 C.0 D.20
C
课堂检测
拓展提升
解:a>b时,根据题意得:c=m+a+b=2(a+b)=20,即a+b=10,
将a=10代入得:b=0,
经检验符合题意,
a<b时,m=b-a,c=b-a+a+b=2b=20,
解得:b=10,
经检验a=b,不合题意,舍去,
则b的值为0.
课堂检测
课堂检测
拓展提升
2、如图,文化广场上摆了一些桌子,若并排摆n张桌子,可同时容纳多少人?当n=20时,可同时容纳多少人?
解: , ,
1
1
2
n
1
2
……
……
(1)
(2)
(n)
当 时,可同时容纳:
(人).
3、一辆卡车在行驶时平均每小时耗油8升,行驶前油箱中有油80升.
⑴用代数式表示行驶x小时后,油箱中的剩余油量
Q=______;
⑵计算行驶2小时,5小时,8小时后,油箱中的剩余油量。
⑶这里,能求x=12小时时剩余油量Q的值吗?
80—8x
拓展提升
课堂检测
当x=2小时
(2)解:
Q=80- 8x
=80-8×2
=64(升)
当x=5小时
Q=80- 8x
=80-8×5
=40(升)
当x=8小时
Q=80- 8x
=80-8×8
=16(升)
(3)解:
当x=12小时
Q=80- 8x=80-8×12
=-16(升)<0
没有实际意义,不能求出剩余油量
本题中的x不能取负数和大于10的值
代数式里的字母虽然可以取不同的数值,但是这些数值不能使代数式和它表示的实际问题失去意义。
代数式的值
概念
应用
用数值代替代数式中的 ,
按照代数式中的 关系计算得出的结果叫做代数式的值
运算
字母
直接代入求值
列代数式求值
整体代入求值
步骤
1. 代入
2. 计算
课堂总结
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
