小学数学人教版六年级上倒数的认识说课课件(共43张PPT)
文档属性
| 名称 | 小学数学人教版六年级上倒数的认识说课课件(共43张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-08 17:43:30 | ||
图片预览








文档简介
(共43张PPT)
倒数的认识
说课流程
说教材
说教法学法
一
三
说教学过程
四
二
说学情
五
说板书设计
一、说教材
地位与作用
“倒数的认识”是人教版数学六年级上册第三单元中的内容,它是在分数乘法的基础上进行教学的,为后面学习分数除法做准备,因为除以分数等于乘这个分数的倒数,所以“倒数”是分数除法计算的关键,它沟通了分数乘法和除法的计算,起着承前启后的桥梁作用。
教学目标
知识与技能目标:
1、理解倒数的意义;
2、掌握求一个数倒数的方法。
过程与方法目标:
让学生主动参与观察、交流、探究等活动,经历探索求倒数方法的过程。
情感态度与价值观目标:
通过自主探索、合作交流,培养学生爱学数学、乐学数学的情感。
目标
重点
理解倒数的意义;熟练掌握求一个数的倒数的方法。
难点
理解倒数相互依存的关系。
教学重、难点
二、说学情
六年级学生已具备一定的观察、类比事物的能力,能够进行合作探究学习,同时,我们班学生思维比较活跃,对于分数的认识和分数乘法的计算掌握较好,因此,我采用直入主题的方法,通过让学生比较一组分数乘法中两个因数和积的特点,来引导学生发现倒数的特征并理解倒数的意义,然后让学生在寻找一个数的倒数的过程中自主探究,逐步总结出求一个数倒数的方法。
三、说教法学法
组织者
引导者
合作者
教师
学生
观察
比较
交流
归纳
四、说教学过程
1
创设情境,引入概念(约3分钟)
3
观察探究,归纳方法(约8分钟)
4
辨析比较,弄清特例(约6分钟)
5
巩固练习,拓展提高(约10分钟)
6
总结评价,内化提升(约5分钟)
2
讨论交流,理解意义(约8分钟)
(一)创设情境,引入概念
客上天然居
居然天上客
人过大佛寺
寺佛大过人
一个数和它倒数的和是2,这个数是( )
例如, 和 的
因为0可以看作 、 、 等,但是把分子分母调换位置后的分母是0,而0不能作分母,所以0没有倒数。
设计力求让学生成为学习的主人,做到“一切真理都要由学生自己获得或由他们重新发现,至少由他们重建。
讨论交流,理解意义(约8分钟)
整数 带分数 小数
乘积是1的两个数互为倒数
乘积是1的两个数互为倒数!
理解倒数相互依存的关系。
所以分子分母调换位置还是 ,所以1的倒数还是1.
3、同桌互相问、互相说
1和0没有找到它们的倒数,是不是所有的数都有倒数呢?
2、举出几个假分数的倒数
巩固练习2:我来当名医
作业做得快的同学,自由结合讨论,有困难的可以请教老师。
说一说你是怎样求一个数的倒数呢 ?
乘积是1,我们就说 和 互为倒数,也可以说成
观察: 找规律
吞
杏
士
吴
呆
干
在我们的数学王国中也有这样交换位置的数.
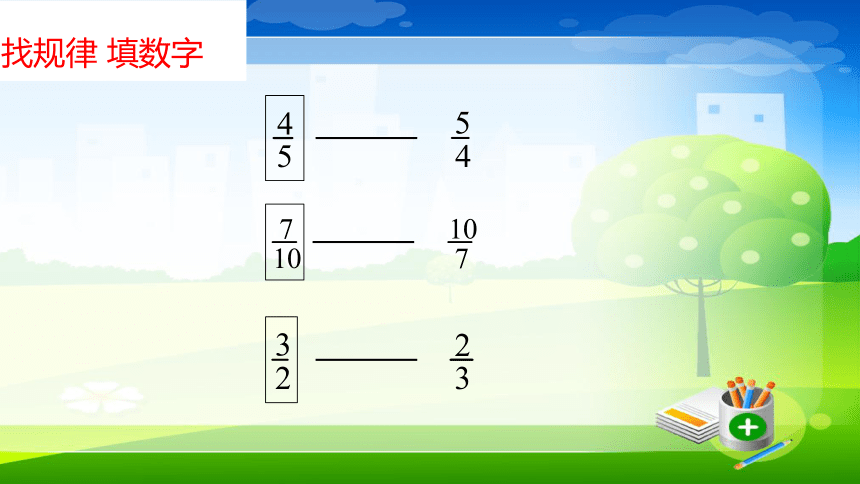
找规律 填数字
倒数的认识
你想知道什么?
学习重点:
一、什么是倒数?
二、怎样求一个数的倒数?
【设计意图】
在这个环节中,我从学生喜闻乐见的故事引入,更接近生活,更能让学生接受,从而激发学生深厚的学习兴趣和求知欲望,快速地进入学习状态。
乘积是 1 的两个数互为倒数。
倒数
它们的乘积都等于1
是什么意思?
×
=1
×
=1
×
= 1
(二)讨论交流,理解意义
看看得数有什么特点?
乘积是1的两个数互为倒数。例如, 和 的
乘积是1,我们就说 和 互为倒数,也可以说成
的倒数是 , 的倒数是
倒数是指两个数之间的关系,这两个数相互依存,一个数不能叫倒数。
【设计意图】
此处在学生自学的基础上,让学生举例说明倒数,积累感性材料,引导学生重点理解倒数意义的关键点。
(三)观察探究,归纳方法
第一步:好朋友-手牵手
第二步:我来试试看,我能行
说一说你是怎样求一个数的倒数呢 ?
局限性
从倒数的意义或者因数×因数=乘积的关系的角度来看
第三步:回顾交流
求一个数的倒数,
可以用1去除以这个数
求一个数的倒数,可以把这个数的分子、分母交换位置。
有没有一种更简单的方法来求一个数的倒数呢
从倒数特点的角度来看
试着写出 、 的倒数。
3
5
5
3
分子、分母调换位置
7
2
2
7
分子、分母调换位置
强调:倒数可以用“
”或“→”表示,不能用“=”
【设计意图】
此环节引导学生在仔细观察数据特征的基础上,细心体会分子与分母的位置关系,尝试发现求倒数的方法。设计力求让学生成为学习的主人,做到“一切真理都要由学生自己获得或由他们重新发现,至少由他们重建。”
说说下面哪两个数互为倒数。
1和0没有找到它们的倒数,是不是所有的数都有倒数呢?
1
那1和0有没有倒数?
它们的倒数是多少呢?
4
6
(四)辨析比较,弄清特例
0
因为1×1=1,所以1的倒数还是1.
因为1= ,
所以分子分母调换位置还是 ,所以1的倒数还是1.
1的倒数是它本身
0有没有倒数呢?
一个数和它倒数的和是2,这个数是( )
所以分子分母调换位置还是 ,所以1的倒数还是1.
1、举出几个真分数的倒数
乘积是1的两个数互为倒数
因为1= ,
因为0和任何数的乘积都等于0,不等于1,所以0没有倒数。
所以分子分母调换位置还是 ,所以1的倒数还是1.
因为1×1=1,所以1的倒数还是1.
2、举出几个假分数的倒数
求一个数的倒数,可以把这个数的分子、分母交换位置。
怎样求一个数的倒数呢?
乘积是1,我们就说 和 互为倒数,也可以说成
巩固练习1:开火车,说倒数
本环节这样设计,既突出本课的重点,又有利于突破难点;
2、整数(0除外)、带分数、小数先转化成真分数或假分数形式,再把分子、分母调换位置。
因为0和任何数的乘积都等于0,不等于1,所以0没有倒数。
因为0可以看作 、 、 等,但是把分子分母调换位置后的分母是0,而0不能作分母,所以0没有倒数。
1的倒数是它本身
0没有倒数
【设计意图】
本环节这样设计,既突出本课的重点,又有利于突破难点;既有对刚刚学过的倒数求法的运用,又使学生产生新的认知冲突:1的倒数为什么是它本身?为什么0没有倒数?这样学生在宽松的氛围里,勇于发言、敢于辩论。
(五)巩固练习,拓展提高
1、举出几个真分数的倒数
2、举出几个假分数的倒数
3、同桌互相问、互相说
巩固练习1:开火车,说倒数
因为 ,
所以 是倒数。
× =1
4
5
5
4
5
4
因为 ,
所以 是倒数。
× =1
4
5
5
4
5
4
×
因为 ,
所以 和 互为倒数。
× =1
3
5
5
3
3
5
5
3
因为 ,
所以 和 互为倒数。
× =1
3
5
5
3
3
5
5
3
√
1的倒数是1,
0的倒数是0。
1的倒数是1,
0的倒数是0。
×
巩固练习2:我来当名医
1.填空:
×( )= ×( )= ×( )
2.一个数和它倒数的和是2,这个数是( )
3.最小的质数的倒数是多少?
拓展练习
作业做得快的同学,自由结合讨论,有困难的可以请教老师。
我们除了学过的真分数、假分数还学过哪些形式的数?
整数 带分数 小数
0除外
课外延伸
它们有没有倒数?它们的倒数该怎么求呢?
【设计意图】
本环节我依据教学目标和学生在学习中存在的问题,设计有针对性、层次分明的练习题组,让学生在解决这些问题的过程中,进一步理解、巩固新知,训练思维的灵活性、敏捷性、创造性,使学生的创新精神和实践能力得到进一步提高。
我们今天学习了什么?
什么叫倒数?
1、真分数或者假分数直接将分子与分母调换位置。
2、整数(0除外)、带分数、小数先转化成真分数或假分数形式,再把分子、分母调换位置。
乘积是1的两个数互为倒数!
倒数!
怎样求一个数的倒数呢?
(六)总结评价,内化提升
五、说板书设计
倒数的认识
什么是倒数?
怎样求一个数的倒数?
乘积是1的两个数互为倒数
分子、分母颠倒位置
1的倒数是它本身;0没有倒数
×
=1
×
=1
→
→
【设计意图】
此处在学生自学的基础上,让学生举例说明倒数,积累感性材料,引导学生重点理解倒数意义的关键点。
(三)观察探究,归纳方法
第一步:好朋友-手牵手
因为0和任何数的乘积都等于0,不等于1,所以0没有倒数。
因为0可以看作 、 、 等,但是把分子分母调换位置后的分母是0,而0不能作分母,所以0没有倒数。
1.填空:
×( )= ×( )= ×( )
2.一个数和它倒数的和是2,这个数是( )
3.最小的质数的倒数是多少?
拓展练习
作业做得快的同学,自由结合讨论,有困难的可以请教老师。
我们今天学习了什么?
什么叫倒数?
1、真分数或者假分数直接将分子与分母调换位置。
2、整数(0除外)、带分数、小数先转化成真分数或假分数形式,再把分子、分母调换位置。
乘积是1的两个数互为倒数!
倒数!
怎样求一个数的倒数呢?
(六)总结评价,内化提升
五、说板书设计
倒数的认识
什么是倒数?
怎样求一个数的倒数?
乘积是1的两个数互为倒数
分子、分母颠倒位置
1的倒数是它本身;0没有倒数
×
=1
×
=1
→
→
倒数的认识
说课流程
说教材
说教法学法
一
三
说教学过程
四
二
说学情
五
说板书设计
一、说教材
地位与作用
“倒数的认识”是人教版数学六年级上册第三单元中的内容,它是在分数乘法的基础上进行教学的,为后面学习分数除法做准备,因为除以分数等于乘这个分数的倒数,所以“倒数”是分数除法计算的关键,它沟通了分数乘法和除法的计算,起着承前启后的桥梁作用。
教学目标
知识与技能目标:
1、理解倒数的意义;
2、掌握求一个数倒数的方法。
过程与方法目标:
让学生主动参与观察、交流、探究等活动,经历探索求倒数方法的过程。
情感态度与价值观目标:
通过自主探索、合作交流,培养学生爱学数学、乐学数学的情感。
目标
重点
理解倒数的意义;熟练掌握求一个数的倒数的方法。
难点
理解倒数相互依存的关系。
教学重、难点
二、说学情
六年级学生已具备一定的观察、类比事物的能力,能够进行合作探究学习,同时,我们班学生思维比较活跃,对于分数的认识和分数乘法的计算掌握较好,因此,我采用直入主题的方法,通过让学生比较一组分数乘法中两个因数和积的特点,来引导学生发现倒数的特征并理解倒数的意义,然后让学生在寻找一个数的倒数的过程中自主探究,逐步总结出求一个数倒数的方法。
三、说教法学法
组织者
引导者
合作者
教师
学生
观察
比较
交流
归纳
四、说教学过程
1
创设情境,引入概念(约3分钟)
3
观察探究,归纳方法(约8分钟)
4
辨析比较,弄清特例(约6分钟)
5
巩固练习,拓展提高(约10分钟)
6
总结评价,内化提升(约5分钟)
2
讨论交流,理解意义(约8分钟)
(一)创设情境,引入概念
客上天然居
居然天上客
人过大佛寺
寺佛大过人
一个数和它倒数的和是2,这个数是( )
例如, 和 的
因为0可以看作 、 、 等,但是把分子分母调换位置后的分母是0,而0不能作分母,所以0没有倒数。
设计力求让学生成为学习的主人,做到“一切真理都要由学生自己获得或由他们重新发现,至少由他们重建。
讨论交流,理解意义(约8分钟)
整数 带分数 小数
乘积是1的两个数互为倒数
乘积是1的两个数互为倒数!
理解倒数相互依存的关系。
所以分子分母调换位置还是 ,所以1的倒数还是1.
3、同桌互相问、互相说
1和0没有找到它们的倒数,是不是所有的数都有倒数呢?
2、举出几个假分数的倒数
巩固练习2:我来当名医
作业做得快的同学,自由结合讨论,有困难的可以请教老师。
说一说你是怎样求一个数的倒数呢 ?
乘积是1,我们就说 和 互为倒数,也可以说成
观察: 找规律
吞
杏
士
吴
呆
干
在我们的数学王国中也有这样交换位置的数.
找规律 填数字
倒数的认识
你想知道什么?
学习重点:
一、什么是倒数?
二、怎样求一个数的倒数?
【设计意图】
在这个环节中,我从学生喜闻乐见的故事引入,更接近生活,更能让学生接受,从而激发学生深厚的学习兴趣和求知欲望,快速地进入学习状态。
乘积是 1 的两个数互为倒数。
倒数
它们的乘积都等于1
是什么意思?
×
=1
×
=1
×
= 1
(二)讨论交流,理解意义
看看得数有什么特点?
乘积是1的两个数互为倒数。例如, 和 的
乘积是1,我们就说 和 互为倒数,也可以说成
的倒数是 , 的倒数是
倒数是指两个数之间的关系,这两个数相互依存,一个数不能叫倒数。
【设计意图】
此处在学生自学的基础上,让学生举例说明倒数,积累感性材料,引导学生重点理解倒数意义的关键点。
(三)观察探究,归纳方法
第一步:好朋友-手牵手
第二步:我来试试看,我能行
说一说你是怎样求一个数的倒数呢 ?
局限性
从倒数的意义或者因数×因数=乘积的关系的角度来看
第三步:回顾交流
求一个数的倒数,
可以用1去除以这个数
求一个数的倒数,可以把这个数的分子、分母交换位置。
有没有一种更简单的方法来求一个数的倒数呢
从倒数特点的角度来看
试着写出 、 的倒数。
3
5
5
3
分子、分母调换位置
7
2
2
7
分子、分母调换位置
强调:倒数可以用“
”或“→”表示,不能用“=”
【设计意图】
此环节引导学生在仔细观察数据特征的基础上,细心体会分子与分母的位置关系,尝试发现求倒数的方法。设计力求让学生成为学习的主人,做到“一切真理都要由学生自己获得或由他们重新发现,至少由他们重建。”
说说下面哪两个数互为倒数。
1和0没有找到它们的倒数,是不是所有的数都有倒数呢?
1
那1和0有没有倒数?
它们的倒数是多少呢?
4
6
(四)辨析比较,弄清特例
0
因为1×1=1,所以1的倒数还是1.
因为1= ,
所以分子分母调换位置还是 ,所以1的倒数还是1.
1的倒数是它本身
0有没有倒数呢?
一个数和它倒数的和是2,这个数是( )
所以分子分母调换位置还是 ,所以1的倒数还是1.
1、举出几个真分数的倒数
乘积是1的两个数互为倒数
因为1= ,
因为0和任何数的乘积都等于0,不等于1,所以0没有倒数。
所以分子分母调换位置还是 ,所以1的倒数还是1.
因为1×1=1,所以1的倒数还是1.
2、举出几个假分数的倒数
求一个数的倒数,可以把这个数的分子、分母交换位置。
怎样求一个数的倒数呢?
乘积是1,我们就说 和 互为倒数,也可以说成
巩固练习1:开火车,说倒数
本环节这样设计,既突出本课的重点,又有利于突破难点;
2、整数(0除外)、带分数、小数先转化成真分数或假分数形式,再把分子、分母调换位置。
因为0和任何数的乘积都等于0,不等于1,所以0没有倒数。
因为0可以看作 、 、 等,但是把分子分母调换位置后的分母是0,而0不能作分母,所以0没有倒数。
1的倒数是它本身
0没有倒数
【设计意图】
本环节这样设计,既突出本课的重点,又有利于突破难点;既有对刚刚学过的倒数求法的运用,又使学生产生新的认知冲突:1的倒数为什么是它本身?为什么0没有倒数?这样学生在宽松的氛围里,勇于发言、敢于辩论。
(五)巩固练习,拓展提高
1、举出几个真分数的倒数
2、举出几个假分数的倒数
3、同桌互相问、互相说
巩固练习1:开火车,说倒数
因为 ,
所以 是倒数。
× =1
4
5
5
4
5
4
因为 ,
所以 是倒数。
× =1
4
5
5
4
5
4
×
因为 ,
所以 和 互为倒数。
× =1
3
5
5
3
3
5
5
3
因为 ,
所以 和 互为倒数。
× =1
3
5
5
3
3
5
5
3
√
1的倒数是1,
0的倒数是0。
1的倒数是1,
0的倒数是0。
×
巩固练习2:我来当名医
1.填空:
×( )= ×( )= ×( )
2.一个数和它倒数的和是2,这个数是( )
3.最小的质数的倒数是多少?
拓展练习
作业做得快的同学,自由结合讨论,有困难的可以请教老师。
我们除了学过的真分数、假分数还学过哪些形式的数?
整数 带分数 小数
0除外
课外延伸
它们有没有倒数?它们的倒数该怎么求呢?
【设计意图】
本环节我依据教学目标和学生在学习中存在的问题,设计有针对性、层次分明的练习题组,让学生在解决这些问题的过程中,进一步理解、巩固新知,训练思维的灵活性、敏捷性、创造性,使学生的创新精神和实践能力得到进一步提高。
我们今天学习了什么?
什么叫倒数?
1、真分数或者假分数直接将分子与分母调换位置。
2、整数(0除外)、带分数、小数先转化成真分数或假分数形式,再把分子、分母调换位置。
乘积是1的两个数互为倒数!
倒数!
怎样求一个数的倒数呢?
(六)总结评价,内化提升
五、说板书设计
倒数的认识
什么是倒数?
怎样求一个数的倒数?
乘积是1的两个数互为倒数
分子、分母颠倒位置
1的倒数是它本身;0没有倒数
×
=1
×
=1
→
→
【设计意图】
此处在学生自学的基础上,让学生举例说明倒数,积累感性材料,引导学生重点理解倒数意义的关键点。
(三)观察探究,归纳方法
第一步:好朋友-手牵手
因为0和任何数的乘积都等于0,不等于1,所以0没有倒数。
因为0可以看作 、 、 等,但是把分子分母调换位置后的分母是0,而0不能作分母,所以0没有倒数。
1.填空:
×( )= ×( )= ×( )
2.一个数和它倒数的和是2,这个数是( )
3.最小的质数的倒数是多少?
拓展练习
作业做得快的同学,自由结合讨论,有困难的可以请教老师。
我们今天学习了什么?
什么叫倒数?
1、真分数或者假分数直接将分子与分母调换位置。
2、整数(0除外)、带分数、小数先转化成真分数或假分数形式,再把分子、分母调换位置。
乘积是1的两个数互为倒数!
倒数!
怎样求一个数的倒数呢?
(六)总结评价,内化提升
五、说板书设计
倒数的认识
什么是倒数?
怎样求一个数的倒数?
乘积是1的两个数互为倒数
分子、分母颠倒位置
1的倒数是它本身;0没有倒数
×
=1
×
=1
→
→
