人教版数学六年级上册 3分数除法单元解读 课件(19张ppt)
文档属性
| 名称 | 人教版数学六年级上册 3分数除法单元解读 课件(19张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 49.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-08 00:00:00 | ||
图片预览




文档简介
聚焦除法运算本质 凸显运算一致性
——《分数除法》单元整体教学解读
说课过程
01 单元整体解读
02 重点课时设计思考
01
单元整体解读
研课标
做前测
理教材
整框架
研课标 明方向
《义务教育数学课程标准(2022年版)》:
感悟数的运算以及运算之间的关系,体会数的运算本质上的一致性,形成运算能力和推理意识。(P.18)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}第
三
学
段
内容
要求
能进行简单的小数、分数四则运算和混合运算,感悟运算的一致性,发展运算能力和推理意识。
学业
要求
能进行简单小数和分数的四则运算和混合运算(不超过三步),
并说明运算过程
教学
提示
数的运算的教学应注重对整数、小数和分数四则运算的统筹,
感悟计数单位在运算中的作用,让学生进一步感悟运算的一致性。
运算的一致性
运算的一致性
计数单位
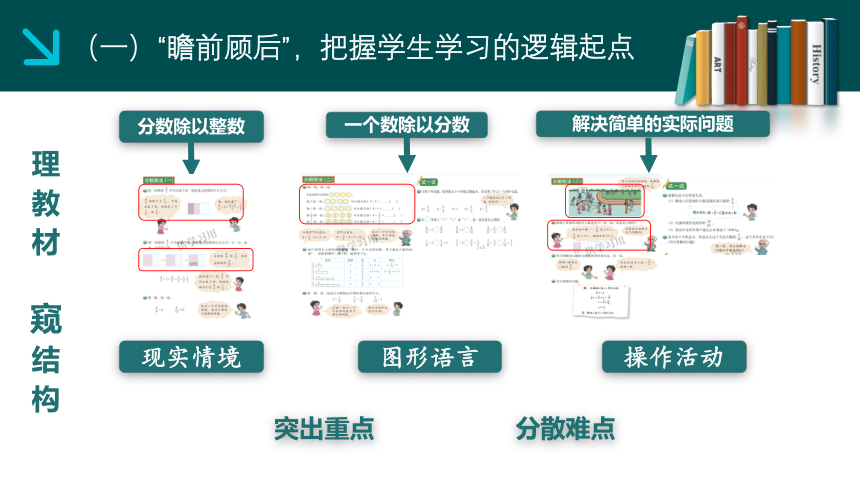
(一)“瞻前顾后”,把握学生学习的逻辑起点
理教材 窥结构
分数除以整数
一个数除以分数
解决简单的实际问题
现实情境
图形语言
操作活动
突出重点
分散难点
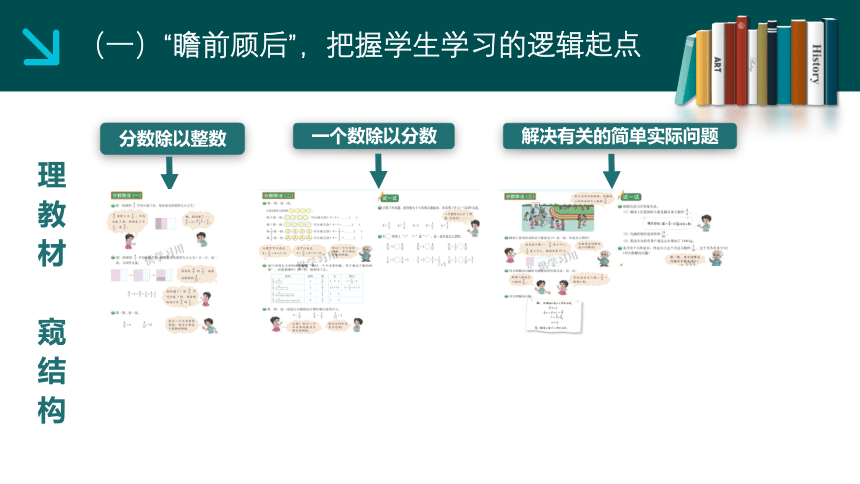
理教材 窥结构
(一)“瞻前顾后”,把握学生学习的逻辑起点
分数除以整数
一个数除以分数
解决有关的简单实际问题
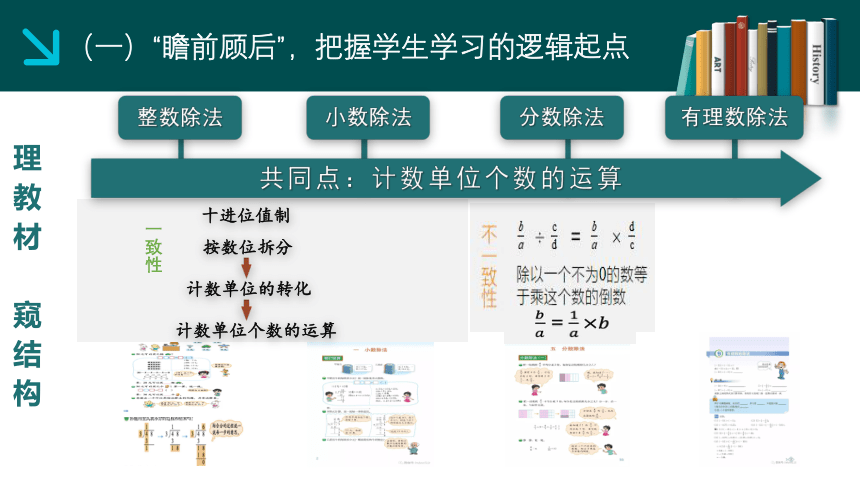
整数除法
除法的认识
小数除法
分数除法
有理数除法
除数是整数的小数除法
分数除以整数
两三位数除以一(两)位数
除数是小数的小数除法
除数是分数的除法
十进位值制
按数位拆分
计数单位的转化
计数单位个数的运算
一致性
(一)“瞻前顾后”,把握学生学习的逻辑起点
理教材 窥结构
共同点:计数单位个数的运算
理教材 窥结构
(二)“左顾右盼”,感悟不同版本的精彩纷呈
{5940675A-B579-460E-94D1-54222C63F5DA}任务序列
北师版
人教版
西师版
分数除以整数
一个数除以分数
分数除法的应用
利于融通意义
利于理解算理
思考:算法的过早呈现,学生是否还有欲望继续探究一个数除以分数的算理?
做前测 知起点
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}维度
学生作品
人数占比
前测
后测
教师访谈
93%
约93%
50%
约13%
9%
2%
95%
20%
10%
超50%
超80%
1.
2.
3.
1.
2.
(1) (2)
算法
算理
观点①:知道算法后忽视算理探索。
观点②:分数除法算理难讲、难懂。
唤醒经验
迁移经验
发现共性
①
②
③
(1)
(2)
①
②
③
①
②
②
①
①
②
《分数除法》前测题
1.计算下面各题,请写出自己的计算过程。
(1)56÷4 (2)3.6÷2
2.你能用解决整数除法、小数除法计算中的经验解决下面的问题吗?可以用画一画、写一写等方法。
(1)把一张纸的310平均分成3份,每份是多少?
(2)把一张纸的25平均分成3份,每份是多少?
3.通过以上计算,你有什么发现?请写下自己的想法。
?
《分数除法》后测题
1.计算,请写出计算过程。
59÷4= 23÷37=
2.我们在计算“a÷b(b≠0)”时,用“a÷b=a×1b”,也就是“除以一个不为零的数等于乘它的倒数”。你知道为什么可以这样做吗?请写下自己的想法。
?
能关注算法的多
VS
能关注算理的少
能正确计算的多
VS
能理解算理的少
能迁移经验的多
VS
能发现共性的少
整框架 定路径
运算一致性
分数除法(一)
分数除法(二)
+1课时
分数除法应用
单元引导课
解释乘倒数的算法
为了实现迁移,感悟运算一致性,通过回顾学习历程,唤醒已有经验,再引导猜想分数除法怎么学。这样,经历本单元前4课时的学习,将分数除法运算融入到已有的整数、小数除法中,建立不同数系的除法运算的联系,促进学生对运算一致性的感悟。
迁移已有学习经验,借助直观模型,把“细分计数单位”作为核心要素,让学生的丰富思维方法得以展现,深刻感悟到分数除法其实是细分计数单位后的运算。
弱化过早提炼算法对探索算理的负面影响
沟通算理,形成通法。
新课标将方程内容移至第四学段,因此我们弱化了方程,利用数量关系及乘除互逆,实现算术法与代数法的并行,有效理解除法的本质意义。
(一)改变序列,夯实过程
(二)拉长过程,强化算理
(三)沟通联系,体现一致
(四)弱化方程,理解意义
单元主题
课时安排
核心要素
主要目标
关键任务
分 数 除 法
对接经验
理解算理
沟通算理
互通互联
课时一
课时二
课时三
课时四
课时五
单元引导课
分数除以整数
一个数除以分数
解释乘倒数的算法
分数除法应用
细分计数单位
细分计数单位
细分计数单位
细分计数单位
数量关系
唤醒经验
寻找路径
感悟意义
理解算理
多元表征
理解算理
沟通算理
形成通法
理清关系
实践应用
1.回顾意义算理算法
2.思考:分数除法怎么学
1.探究整数除以分数
2.解决问题
1.举例验证,解释算理
2.沟通联系,回顾整理
1.尝试解决
2.交流方法
3.解决问题
运 算 一 致 性
1.探究????????÷2
2. 探究????????÷3
3.理清算理
?
4
5
3
5
重点课时设计思考
重点课时设计思考
整体设计
设计思考
整体设计
基于“运算一致性”视角下《分数除以整数》学习路径重建图
任务一
目标:算法辨析,
感悟运算一致性
通过 ÷2的各种算法比较,感悟整数、小数、分数除法都是计数单位个数的运算。
4
5
任务二
目标:细分单位,
疏通分数除法通法
通过 ÷2的算法探究,在细分计数单位的过程中寻找合适的分数单位,疏通分数除法的通法。
3
5
任务三
目标:贯通联系,
构建数运算模型
沟通分数除法与整数除法、小数除法间的联系,突破数系限制,抽象除法运算的模型。
(一)唤醒经验,在联系中产生猜想
设计思考
思考:为什么用除法计算?
猜想:分数除法和整数、小数除法的意义一样,那么在算理上有什么相通的地方呢?
(二)
设计思考
初探算理,在比较中感悟运算的一致性
通过三种算法的探究,充分运用迁移、转化思想,利用已有知识算一算或借助直观图画一画,探究“计算的过程中有什么相同之处” ,聚焦“4÷2”,从图形到算式,再从算式到图形,数形结合,进一步加深学生对分数除法算理的理解。
设计思考
(三)聚焦问题,在细分单位中疏通分数除法的通法
核心问题:4个五分之一怎么平均分成3份?
层层推进 运算本质
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
比较
第一
层次
横分
竖分
第二
层次
第三
层次
设计思考
(四)融会贯通,在内化中抽象数运算的模型
正向
逆向
通过两道题,从正向和逆向两个角度帮助学生内化算理算法。
借助微课回顾与梳理,发现分数除法与整数除法、小数除法仅仅是数域的不同,算理是相通的:进行计数单位个数的运算,有利于学生认知的结构化,体现知识的贯通性、整体性与一致性。
整体设计
运算一致性
唤 醒
感 悟
疏 通
构 建
计数单位
感 谢 聆 听
——《分数除法》单元整体教学解读
说课过程
01 单元整体解读
02 重点课时设计思考
01
单元整体解读
研课标
做前测
理教材
整框架
研课标 明方向
《义务教育数学课程标准(2022年版)》:
感悟数的运算以及运算之间的关系,体会数的运算本质上的一致性,形成运算能力和推理意识。(P.18)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}第
三
学
段
内容
要求
能进行简单的小数、分数四则运算和混合运算,感悟运算的一致性,发展运算能力和推理意识。
学业
要求
能进行简单小数和分数的四则运算和混合运算(不超过三步),
并说明运算过程
教学
提示
数的运算的教学应注重对整数、小数和分数四则运算的统筹,
感悟计数单位在运算中的作用,让学生进一步感悟运算的一致性。
运算的一致性
运算的一致性
计数单位
(一)“瞻前顾后”,把握学生学习的逻辑起点
理教材 窥结构
分数除以整数
一个数除以分数
解决简单的实际问题
现实情境
图形语言
操作活动
突出重点
分散难点
理教材 窥结构
(一)“瞻前顾后”,把握学生学习的逻辑起点
分数除以整数
一个数除以分数
解决有关的简单实际问题
整数除法
除法的认识
小数除法
分数除法
有理数除法
除数是整数的小数除法
分数除以整数
两三位数除以一(两)位数
除数是小数的小数除法
除数是分数的除法
十进位值制
按数位拆分
计数单位的转化
计数单位个数的运算
一致性
(一)“瞻前顾后”,把握学生学习的逻辑起点
理教材 窥结构
共同点:计数单位个数的运算
理教材 窥结构
(二)“左顾右盼”,感悟不同版本的精彩纷呈
{5940675A-B579-460E-94D1-54222C63F5DA}任务序列
北师版
人教版
西师版
分数除以整数
一个数除以分数
分数除法的应用
利于融通意义
利于理解算理
思考:算法的过早呈现,学生是否还有欲望继续探究一个数除以分数的算理?
做前测 知起点
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}维度
学生作品
人数占比
前测
后测
教师访谈
93%
约93%
50%
约13%
9%
2%
95%
20%
10%
超50%
超80%
1.
2.
3.
1.
2.
(1) (2)
算法
算理
观点①:知道算法后忽视算理探索。
观点②:分数除法算理难讲、难懂。
唤醒经验
迁移经验
发现共性
①
②
③
(1)
(2)
①
②
③
①
②
②
①
①
②
《分数除法》前测题
1.计算下面各题,请写出自己的计算过程。
(1)56÷4 (2)3.6÷2
2.你能用解决整数除法、小数除法计算中的经验解决下面的问题吗?可以用画一画、写一写等方法。
(1)把一张纸的310平均分成3份,每份是多少?
(2)把一张纸的25平均分成3份,每份是多少?
3.通过以上计算,你有什么发现?请写下自己的想法。
?
《分数除法》后测题
1.计算,请写出计算过程。
59÷4= 23÷37=
2.我们在计算“a÷b(b≠0)”时,用“a÷b=a×1b”,也就是“除以一个不为零的数等于乘它的倒数”。你知道为什么可以这样做吗?请写下自己的想法。
?
能关注算法的多
VS
能关注算理的少
能正确计算的多
VS
能理解算理的少
能迁移经验的多
VS
能发现共性的少
整框架 定路径
运算一致性
分数除法(一)
分数除法(二)
+1课时
分数除法应用
单元引导课
解释乘倒数的算法
为了实现迁移,感悟运算一致性,通过回顾学习历程,唤醒已有经验,再引导猜想分数除法怎么学。这样,经历本单元前4课时的学习,将分数除法运算融入到已有的整数、小数除法中,建立不同数系的除法运算的联系,促进学生对运算一致性的感悟。
迁移已有学习经验,借助直观模型,把“细分计数单位”作为核心要素,让学生的丰富思维方法得以展现,深刻感悟到分数除法其实是细分计数单位后的运算。
弱化过早提炼算法对探索算理的负面影响
沟通算理,形成通法。
新课标将方程内容移至第四学段,因此我们弱化了方程,利用数量关系及乘除互逆,实现算术法与代数法的并行,有效理解除法的本质意义。
(一)改变序列,夯实过程
(二)拉长过程,强化算理
(三)沟通联系,体现一致
(四)弱化方程,理解意义
单元主题
课时安排
核心要素
主要目标
关键任务
分 数 除 法
对接经验
理解算理
沟通算理
互通互联
课时一
课时二
课时三
课时四
课时五
单元引导课
分数除以整数
一个数除以分数
解释乘倒数的算法
分数除法应用
细分计数单位
细分计数单位
细分计数单位
细分计数单位
数量关系
唤醒经验
寻找路径
感悟意义
理解算理
多元表征
理解算理
沟通算理
形成通法
理清关系
实践应用
1.回顾意义算理算法
2.思考:分数除法怎么学
1.探究整数除以分数
2.解决问题
1.举例验证,解释算理
2.沟通联系,回顾整理
1.尝试解决
2.交流方法
3.解决问题
运 算 一 致 性
1.探究????????÷2
2. 探究????????÷3
3.理清算理
?
4
5
3
5
重点课时设计思考
重点课时设计思考
整体设计
设计思考
整体设计
基于“运算一致性”视角下《分数除以整数》学习路径重建图
任务一
目标:算法辨析,
感悟运算一致性
通过 ÷2的各种算法比较,感悟整数、小数、分数除法都是计数单位个数的运算。
4
5
任务二
目标:细分单位,
疏通分数除法通法
通过 ÷2的算法探究,在细分计数单位的过程中寻找合适的分数单位,疏通分数除法的通法。
3
5
任务三
目标:贯通联系,
构建数运算模型
沟通分数除法与整数除法、小数除法间的联系,突破数系限制,抽象除法运算的模型。
(一)唤醒经验,在联系中产生猜想
设计思考
思考:为什么用除法计算?
猜想:分数除法和整数、小数除法的意义一样,那么在算理上有什么相通的地方呢?
(二)
设计思考
初探算理,在比较中感悟运算的一致性
通过三种算法的探究,充分运用迁移、转化思想,利用已有知识算一算或借助直观图画一画,探究“计算的过程中有什么相同之处” ,聚焦“4÷2”,从图形到算式,再从算式到图形,数形结合,进一步加深学生对分数除法算理的理解。
设计思考
(三)聚焦问题,在细分单位中疏通分数除法的通法
核心问题:4个五分之一怎么平均分成3份?
层层推进 运算本质
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
比较
第一
层次
横分
竖分
第二
层次
第三
层次
设计思考
(四)融会贯通,在内化中抽象数运算的模型
正向
逆向
通过两道题,从正向和逆向两个角度帮助学生内化算理算法。
借助微课回顾与梳理,发现分数除法与整数除法、小数除法仅仅是数域的不同,算理是相通的:进行计数单位个数的运算,有利于学生认知的结构化,体现知识的贯通性、整体性与一致性。
整体设计
运算一致性
唤 醒
感 悟
疏 通
构 建
计数单位
感 谢 聆 听
