广东省佛山市2022-2023学年高二下学期期末考试数学试题(含答案)
文档属性
| 名称 | 广东省佛山市2022-2023学年高二下学期期末考试数学试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 551.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-08 12:20:12 | ||
图片预览




文档简介
佛山市2022-2023学年高二下学期期末考试
数学
2023年7月
本试卷共5页,22小题.满分150分.考试用时120分钟.
注意事项:
1. 答卷前,考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上,将条形码横贴在答题卡右上角“条形码粘贴处”.
2. 作答选择题时,选出每小题答案后,用2B铅笔在答题卡上对应题目后面的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案.答案不能答在试卷上.
3. 非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液.不按以上要求作答无效.
4. 考生必须保持答题卡的整洁.考试结束后,请将答题卡交回.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 的展开式中常数项是( )
A. 0 B. 1 C. 2 D. 3
2. 四名志愿者到3个小区开展防诈骗宣传活动,向社区居民普及防诈骗、反诈骗的知识.每名志愿者只去1个小区,每个小区至少安排1名志愿者,则不同的安排方法共有( )
A. 18种 B. 30种 C. 36种 D. 72种
3. 吹气球时,气球的半径r(单位:dm)与体积V(单位:L)之间的函数关系是,估计时气球的膨胀率为( )(参考数据:)
A. 0.2 B. 0.6 C. 1 D. 1.2
4. 根据变量Y和x的成对样本数据,由一元线性回归模型,得到经验回归模型,对应的残差如图所示,则模型误差( )
A. 不满足一元线性回归模型的的假设
B. 不满足一元线性回归模型的的假设
C. 不满足一元线性回归模型的和的假设
D. 满足一元线性回归模型的所有假设
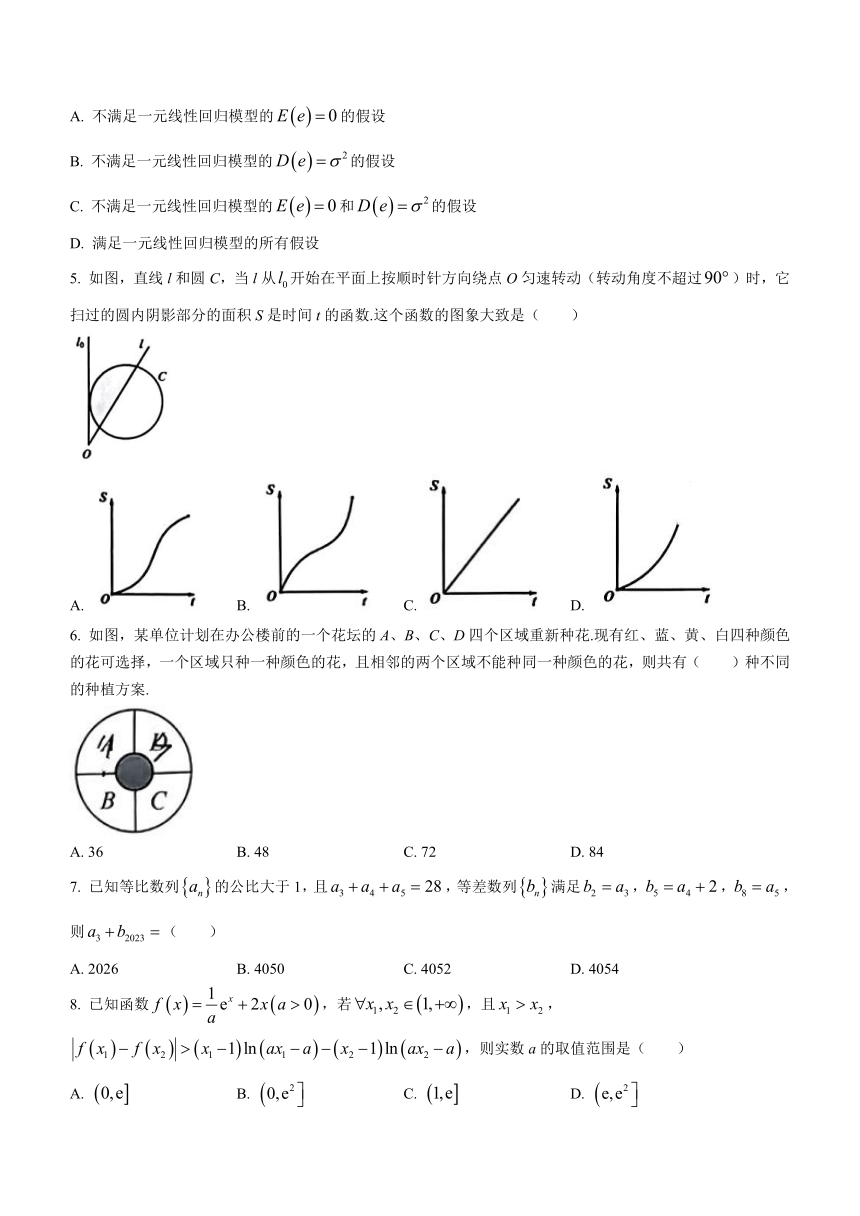
5. 如图,直线l和圆C,当l从开始在平面上按顺时针方向绕点O匀速转动(转动角度不超过)时,它扫过的圆内阴影部分的面积S是时间t的函数.这个函数的图象大致是( )
A. B. C. D.
6. 如图,某单位计划在办公楼前的一个花坛的A、B、C、D四个区域重新种花.现有红、蓝、黄、白四种颜色的花可选择,一个区域只种一种颜色的花,且相邻的两个区域不能种同一种颜色的花,则共有( )种不同的种植方案.
A. 36 B. 48 C. 72 D. 84
7. 已知等比数列的公比大于1,且,等差数列满足,,,则( )
A. 2026 B. 4050 C. 4052 D. 4054
8. 已知函数,若,且,,则实数a的取值范围是( )
A. B. C. D.
二、选择题:本题共4小题.每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9. 已知,则( )
A. B.
C. D.
10. 三名男生和四名女生,按照不同的要求站成一排,则( )
A. 任何两名男生不相邻的排队方案有1440种
B. 若3名男生的顺序一定,则不同的排队方案有210种
C. 甲不站左端,乙不站右端的排队方案有3720种
D. 甲乙两名同学之间恰有2人的不同排队方案有960种
11. 事件A,B满足,,,则( )
A. B. C. D.
12. 记等差数列的前n和为,数列的前k和为,则( )
A. 若,均有,则
B. 若当且仅当时,取得最小值,则
C. 若且,则当且仅当时,取得最小值
D. 若和时,取得最小值,则,
三、填空题:本题共4小题,每小题5分,共20分.其中16题第一空2分,第二空3分.
13. 设随机变量,,则______.
14. 已知成对样本数据,,…,中,,…,不全相等,且所有样本点都在直线上,则这组成对样本数据的样本相关系数______.
15. 直线是曲线的一条切线,则______.
16. 河图、洛书是我国古代流传下来的两幅神秘图案,蕴含了深奥的宇宙星象之理,被誉为“宇宙魔方”.洛书是世界上最古老的三阶幻方(一般地,将连续的正整数1,2,3,…,填入个方格中,使得每行、每列、每条对角线上的数的和相等,这个正方形叫做n阶幻方).记n阶幻方的数之和为,则______,若,则n的最小值为______.
四、解答题:本题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.(10分)
某商家为了提高服务质量,专门开设了顾客反馈热线电话.热线电话共有3个分机专供与顾客通话.设每个分机在每一时刻占线的概率为,并且各个分机是否占线是相互独立的.
(1)求在某一时刻恰好有一个分机占线的概率;
(2)求任一时刻占线的分机个数X的分布列与数学期望.
18.(12分)
已知函数.
(1)讨论的单调性;
(2)求在区间上的最小值与最大值.
19.(12分)
记数列的前n项和为,已知,.
(1)求的通项公式;
(2)若对任意,,求m的最小整数值.
20.(12分)
ChatGPT作为一个基于大型语言模型的聊天机器人,最近成为全球关注的焦点.ChatGPT是一个超强的AI,它能像人类一样聊天交流,甚至能完成撰写邮件、文案、写论文、答辩、编程等任务.专家预言,随着人工智能技术的发展,越来越多的职业可能会被ChatGPT或其他类似的人工智能工具所取代.某地区为了了解ChatGPT的普及情况,统计了该地区从2023年1月至5月使用ChatGPT的用户人数y(万人),详见下表:
x(月份) 1 2 3 4 5
y(万人) 3.6 6.4 11.7 18.8 27.5
(1)根据表中数据信息及模型①与模型②,判断哪一个模型更适合描述变量x和y的变化规律(无需说明理由),并求出y关于x的经验回归方程;
(2)为了进一步了解人们对适应人工智能所将带来的职业结构变化的自信程度(分为“基本适应”和“不适应”)是否跟年龄有关,某部门从该地区随机抽取300人进行调查,调查数据如下表:
基本适应 不适应
年龄小于30岁 100 50
年龄不小于30岁 75 75
根据小概率的独立性检验,分析该地区对职业结构变化的自信程度是否与年龄有关.
附参考数据:,;,.
15 55 979 68 264 1122
0.15 0.1 0.05 0.025 0.01 0.001
2.072 2.706 3.841 5.024 6.635 10.828
21.(12分)
机动车辆保险即汽车保险(简称车险),是指对机动车辆由于自然灾害或意外事故所造成的人身伤亡或财产损失负赔偿责任的一种商业保险.机动车辆保险一般包括交强险和商业险两部分,其中商业险包括基本险和附加险.经验表明新车商业险保费y(单位:元)与购车价格x(单位:元)近似满足函数,且上一年的出险次数决定了下一年的保费倍率.佛山市某机动车辆保险公司将上一年的出险次数与下一年的保费倍率的具体关系制作如下表格:
上一年出险次数 0 1 2 3 4 5次以上(含5次)
下一年保费倍率 85% 100% 125% 150% 175% 200%
连续两年没有出险打7折,连续三年没有出险打6折
王先生于2021年3月份购买了一辆30万元的新车,一直到2022年12月没有出过险,但于2023年买保险前仅出过两次险.
(1)王先生在2023年应交商业险保费多少元?
(2)保险公司计划为前来续保的每一位车主提供抽奖的机会,抽奖规则是:有放回的从装有大小相同的6个红球和4个黑球的袋中任意抽取一个,若第一次抽到红球则奖励100元的奖券,抽到黑球则奖励50元的奖券,第二次开始,每一次抽到红球则奖券数额是上一次奖券数额的2倍,抽到黑球则奖励50元的奖券,车主所获得的奖券可以抵扣续保费.为了激励车主谨慎驾驶,保险公司规定:上一年没有出险的车主可以抽奖6次,车主每增加一次出险就减少一次抽奖机会.记车主第i次抽奖所得的奖券数额的数学期望为.
(i)写出与的递推关系式(其中且);
(ii)若按照保险公司的计划,且王先生不放弃每一次抽奖机会,王先生在2023年续保商业险时,实际支付保费的期望值为多少?
22.(12分)
已知函数.
(1)当时,证明:;
(2)若函数在上只有一个零点,求实数a的取值范围.
佛山市2022-2023学年高二下学期期末考试
数学参考答案
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
题号 1 2 3 4 5 6 7 8
答案 D C A B A D B B
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
题号 9 10 11 12
答案 BC ACD ABC BD
三、填空题:本题共4小题,每小题5分,共20分.其中16题第一空2分,第二空3分.
13. 0.15 14. -1 15. E 16. 136,8
四、解答题:本大题共6小题,共70分,解答须写出必要的文字说明、证明过程或演算步骤.
17.【解析】(1)设事件“恰好有一个分机占线”,……1分
则.……4分
(2)由于各个分机是否占线是相互独立的,则,……6分
所以,,
,.……8分
故X的分布列为:
X 0 1 2 3
P
……9分
所以X的期望(或).……10分
18.【解析】(1)由题知,
所以.……1分
令,解得或.……2分
当x变化时,,的变化情况如下表所示.
x 2
+ 0 - 0 +
……4分
由表可知在区间上单调递减,在区间和上单调递增.……6分
(2)由(1)知,函数的极大值为,极小值为.……8分
又,.……10分
所以,函数在上的最大值为2,最小值为-1.……12分
19.【解析】(1)因为,所以,……1分
两式相减得,即,……3分
又,所以,……4分
所以是首项为3,公差为2的等差数列,……5分
所以.……6分
(2)(法一)因为,设,
所以,……7分
两式相减得:……8分
……10分
所以……11分
因为,所以m的最小整数值是2.……12分
(法二)设,,则,……7分
所以,……8分
所以……9分
所以,即是常数列.……10分
所以,所以.……11分
因为,所以m的最小整数值是2.……12分
20.【解析】(1)选择模型②.……1分
记,则.……2分
由题知,,,,,
所以,……5分
所以,即y关于x的回归方程为.……6分
(2)由题意,得到列联表:
基本适应 不适应 合计
年龄不小于30岁 75 75 150
年龄小于30岁 100 50 150
合计 175 125 300
……7分
零假设为:该地区对职业结构变化的自信程度与年龄无关.……8分
则,……10分
根据的独立性检验,我们可以推断不成立,即认为该地区对职业结构变化的自信程度与年龄有关,此推断犯错误的概率不大于0.01.……12分
21.【解析】(1)王先生于2021年买新车时需交商业险为:元,……1分
由于2021年3月份至2022年3月份没有出险,
所以2022年3月份李先生需交商业险费为:元,……2分
但在2023年1月份出过两次险,
故王先生在2023年3月应交商业险费为:元.……3分
(2)(i)因为袋中装有6个红球和4个黑球,所以从中任意抽取一个是红球的概率为0.6,是黑球的概率为:0.4,……4分
,……5分
当时,车主第i次抽到奖券数额的期望为,
且,……7分
(ii)由(i)知,,
当时,,即,而,
因此是以180为首项,为公比的等比数列,……9分
所以,即,……10分
由于王先生在2023年买保险前出过两次险,故续保时只有4次抽奖机会,4次抽奖获得奖券数额的期望值之和为,……11分
按照保险公司的计划,王先生在2023年续保商业险时,实际支付保费的期望值为:
元.……12分
22.【解析】(1)令,
因为,所以,……1分
令,则在上恒成立,……2分
所以在上单调递减,所以,即在上恒成立,……3分
所以,
令,则在上恒成立,……4分
所以在上单调递减,所以,
即在上恒成立,
所以当时,.……5分
(2)由得,令,……6分
则,令,
当时,,故在上单调递减,……8分
所以,所以,故在上单调递减,……10分
因为,当时,,所以的值域为,
所以,即,所以a的取值范围为.……12分
数学
2023年7月
本试卷共5页,22小题.满分150分.考试用时120分钟.
注意事项:
1. 答卷前,考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上,将条形码横贴在答题卡右上角“条形码粘贴处”.
2. 作答选择题时,选出每小题答案后,用2B铅笔在答题卡上对应题目后面的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案.答案不能答在试卷上.
3. 非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液.不按以上要求作答无效.
4. 考生必须保持答题卡的整洁.考试结束后,请将答题卡交回.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 的展开式中常数项是( )
A. 0 B. 1 C. 2 D. 3
2. 四名志愿者到3个小区开展防诈骗宣传活动,向社区居民普及防诈骗、反诈骗的知识.每名志愿者只去1个小区,每个小区至少安排1名志愿者,则不同的安排方法共有( )
A. 18种 B. 30种 C. 36种 D. 72种
3. 吹气球时,气球的半径r(单位:dm)与体积V(单位:L)之间的函数关系是,估计时气球的膨胀率为( )(参考数据:)
A. 0.2 B. 0.6 C. 1 D. 1.2
4. 根据变量Y和x的成对样本数据,由一元线性回归模型,得到经验回归模型,对应的残差如图所示,则模型误差( )
A. 不满足一元线性回归模型的的假设
B. 不满足一元线性回归模型的的假设
C. 不满足一元线性回归模型的和的假设
D. 满足一元线性回归模型的所有假设
5. 如图,直线l和圆C,当l从开始在平面上按顺时针方向绕点O匀速转动(转动角度不超过)时,它扫过的圆内阴影部分的面积S是时间t的函数.这个函数的图象大致是( )
A. B. C. D.
6. 如图,某单位计划在办公楼前的一个花坛的A、B、C、D四个区域重新种花.现有红、蓝、黄、白四种颜色的花可选择,一个区域只种一种颜色的花,且相邻的两个区域不能种同一种颜色的花,则共有( )种不同的种植方案.
A. 36 B. 48 C. 72 D. 84
7. 已知等比数列的公比大于1,且,等差数列满足,,,则( )
A. 2026 B. 4050 C. 4052 D. 4054
8. 已知函数,若,且,,则实数a的取值范围是( )
A. B. C. D.
二、选择题:本题共4小题.每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9. 已知,则( )
A. B.
C. D.
10. 三名男生和四名女生,按照不同的要求站成一排,则( )
A. 任何两名男生不相邻的排队方案有1440种
B. 若3名男生的顺序一定,则不同的排队方案有210种
C. 甲不站左端,乙不站右端的排队方案有3720种
D. 甲乙两名同学之间恰有2人的不同排队方案有960种
11. 事件A,B满足,,,则( )
A. B. C. D.
12. 记等差数列的前n和为,数列的前k和为,则( )
A. 若,均有,则
B. 若当且仅当时,取得最小值,则
C. 若且,则当且仅当时,取得最小值
D. 若和时,取得最小值,则,
三、填空题:本题共4小题,每小题5分,共20分.其中16题第一空2分,第二空3分.
13. 设随机变量,,则______.
14. 已知成对样本数据,,…,中,,…,不全相等,且所有样本点都在直线上,则这组成对样本数据的样本相关系数______.
15. 直线是曲线的一条切线,则______.
16. 河图、洛书是我国古代流传下来的两幅神秘图案,蕴含了深奥的宇宙星象之理,被誉为“宇宙魔方”.洛书是世界上最古老的三阶幻方(一般地,将连续的正整数1,2,3,…,填入个方格中,使得每行、每列、每条对角线上的数的和相等,这个正方形叫做n阶幻方).记n阶幻方的数之和为,则______,若,则n的最小值为______.
四、解答题:本题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.(10分)
某商家为了提高服务质量,专门开设了顾客反馈热线电话.热线电话共有3个分机专供与顾客通话.设每个分机在每一时刻占线的概率为,并且各个分机是否占线是相互独立的.
(1)求在某一时刻恰好有一个分机占线的概率;
(2)求任一时刻占线的分机个数X的分布列与数学期望.
18.(12分)
已知函数.
(1)讨论的单调性;
(2)求在区间上的最小值与最大值.
19.(12分)
记数列的前n项和为,已知,.
(1)求的通项公式;
(2)若对任意,,求m的最小整数值.
20.(12分)
ChatGPT作为一个基于大型语言模型的聊天机器人,最近成为全球关注的焦点.ChatGPT是一个超强的AI,它能像人类一样聊天交流,甚至能完成撰写邮件、文案、写论文、答辩、编程等任务.专家预言,随着人工智能技术的发展,越来越多的职业可能会被ChatGPT或其他类似的人工智能工具所取代.某地区为了了解ChatGPT的普及情况,统计了该地区从2023年1月至5月使用ChatGPT的用户人数y(万人),详见下表:
x(月份) 1 2 3 4 5
y(万人) 3.6 6.4 11.7 18.8 27.5
(1)根据表中数据信息及模型①与模型②,判断哪一个模型更适合描述变量x和y的变化规律(无需说明理由),并求出y关于x的经验回归方程;
(2)为了进一步了解人们对适应人工智能所将带来的职业结构变化的自信程度(分为“基本适应”和“不适应”)是否跟年龄有关,某部门从该地区随机抽取300人进行调查,调查数据如下表:
基本适应 不适应
年龄小于30岁 100 50
年龄不小于30岁 75 75
根据小概率的独立性检验,分析该地区对职业结构变化的自信程度是否与年龄有关.
附参考数据:,;,.
15 55 979 68 264 1122
0.15 0.1 0.05 0.025 0.01 0.001
2.072 2.706 3.841 5.024 6.635 10.828
21.(12分)
机动车辆保险即汽车保险(简称车险),是指对机动车辆由于自然灾害或意外事故所造成的人身伤亡或财产损失负赔偿责任的一种商业保险.机动车辆保险一般包括交强险和商业险两部分,其中商业险包括基本险和附加险.经验表明新车商业险保费y(单位:元)与购车价格x(单位:元)近似满足函数,且上一年的出险次数决定了下一年的保费倍率.佛山市某机动车辆保险公司将上一年的出险次数与下一年的保费倍率的具体关系制作如下表格:
上一年出险次数 0 1 2 3 4 5次以上(含5次)
下一年保费倍率 85% 100% 125% 150% 175% 200%
连续两年没有出险打7折,连续三年没有出险打6折
王先生于2021年3月份购买了一辆30万元的新车,一直到2022年12月没有出过险,但于2023年买保险前仅出过两次险.
(1)王先生在2023年应交商业险保费多少元?
(2)保险公司计划为前来续保的每一位车主提供抽奖的机会,抽奖规则是:有放回的从装有大小相同的6个红球和4个黑球的袋中任意抽取一个,若第一次抽到红球则奖励100元的奖券,抽到黑球则奖励50元的奖券,第二次开始,每一次抽到红球则奖券数额是上一次奖券数额的2倍,抽到黑球则奖励50元的奖券,车主所获得的奖券可以抵扣续保费.为了激励车主谨慎驾驶,保险公司规定:上一年没有出险的车主可以抽奖6次,车主每增加一次出险就减少一次抽奖机会.记车主第i次抽奖所得的奖券数额的数学期望为.
(i)写出与的递推关系式(其中且);
(ii)若按照保险公司的计划,且王先生不放弃每一次抽奖机会,王先生在2023年续保商业险时,实际支付保费的期望值为多少?
22.(12分)
已知函数.
(1)当时,证明:;
(2)若函数在上只有一个零点,求实数a的取值范围.
佛山市2022-2023学年高二下学期期末考试
数学参考答案
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
题号 1 2 3 4 5 6 7 8
答案 D C A B A D B B
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
题号 9 10 11 12
答案 BC ACD ABC BD
三、填空题:本题共4小题,每小题5分,共20分.其中16题第一空2分,第二空3分.
13. 0.15 14. -1 15. E 16. 136,8
四、解答题:本大题共6小题,共70分,解答须写出必要的文字说明、证明过程或演算步骤.
17.【解析】(1)设事件“恰好有一个分机占线”,……1分
则.……4分
(2)由于各个分机是否占线是相互独立的,则,……6分
所以,,
,.……8分
故X的分布列为:
X 0 1 2 3
P
……9分
所以X的期望(或).……10分
18.【解析】(1)由题知,
所以.……1分
令,解得或.……2分
当x变化时,,的变化情况如下表所示.
x 2
+ 0 - 0 +
……4分
由表可知在区间上单调递减,在区间和上单调递增.……6分
(2)由(1)知,函数的极大值为,极小值为.……8分
又,.……10分
所以,函数在上的最大值为2,最小值为-1.……12分
19.【解析】(1)因为,所以,……1分
两式相减得,即,……3分
又,所以,……4分
所以是首项为3,公差为2的等差数列,……5分
所以.……6分
(2)(法一)因为,设,
所以,……7分
两式相减得:……8分
……10分
所以……11分
因为,所以m的最小整数值是2.……12分
(法二)设,,则,……7分
所以,……8分
所以……9分
所以,即是常数列.……10分
所以,所以.……11分
因为,所以m的最小整数值是2.……12分
20.【解析】(1)选择模型②.……1分
记,则.……2分
由题知,,,,,
所以,……5分
所以,即y关于x的回归方程为.……6分
(2)由题意,得到列联表:
基本适应 不适应 合计
年龄不小于30岁 75 75 150
年龄小于30岁 100 50 150
合计 175 125 300
……7分
零假设为:该地区对职业结构变化的自信程度与年龄无关.……8分
则,……10分
根据的独立性检验,我们可以推断不成立,即认为该地区对职业结构变化的自信程度与年龄有关,此推断犯错误的概率不大于0.01.……12分
21.【解析】(1)王先生于2021年买新车时需交商业险为:元,……1分
由于2021年3月份至2022年3月份没有出险,
所以2022年3月份李先生需交商业险费为:元,……2分
但在2023年1月份出过两次险,
故王先生在2023年3月应交商业险费为:元.……3分
(2)(i)因为袋中装有6个红球和4个黑球,所以从中任意抽取一个是红球的概率为0.6,是黑球的概率为:0.4,……4分
,……5分
当时,车主第i次抽到奖券数额的期望为,
且,……7分
(ii)由(i)知,,
当时,,即,而,
因此是以180为首项,为公比的等比数列,……9分
所以,即,……10分
由于王先生在2023年买保险前出过两次险,故续保时只有4次抽奖机会,4次抽奖获得奖券数额的期望值之和为,……11分
按照保险公司的计划,王先生在2023年续保商业险时,实际支付保费的期望值为:
元.……12分
22.【解析】(1)令,
因为,所以,……1分
令,则在上恒成立,……2分
所以在上单调递减,所以,即在上恒成立,……3分
所以,
令,则在上恒成立,……4分
所以在上单调递减,所以,
即在上恒成立,
所以当时,.……5分
(2)由得,令,……6分
则,令,
当时,,故在上单调递减,……8分
所以,所以,故在上单调递减,……10分
因为,当时,,所以的值域为,
所以,即,所以a的取值范围为.……12分
同课章节目录
