湖北省黄冈市黄州中学(黄冈外校)2022-2023学年高一下学期平行班+宏志班第六次阶段性测试数学试卷(含答案)
文档属性
| 名称 | 湖北省黄冈市黄州中学(黄冈外校)2022-2023学年高一下学期平行班+宏志班第六次阶段性测试数学试卷(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 417.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-08 00:00:00 | ||
图片预览

文档简介
机密★启用前
2023年黄州中学(黄冈外校)高一第二学期第六次阶段性测试
数学试卷
2023年6月1日 考试范围:第六章-第八章;考试时间:120分钟;联合命题:黄冈袭明卓越教育中心
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
第I卷(选择题)
一、单选题(本大题共8小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1. 已知全集,集合,则( )
A. B. C. D.
2. 若点A在平面内,直线l在平面内,点A不在直线l上,下列用集合表示这些语句的描述中,正确的是( )
A. 且 B. 且 C. 且 D. 且
3. 下列说法中正确的是( )
A. 第一象限角是锐角 B. 钝角是第二象限角
C. 终边相同的角一定相等 D. 不相等的角,它们的终边必不相同
4. i为虚数单位,已知复数是纯虚数,则a等于( )
A. B. 1 C. D. 0
5. 已知向量,,若,则( )
A. B. 1 C. D.
6. 已知侧棱长为2a的正三棱锥底面为等边三角形其底面周长为9a,则棱锥的高为( )
A. a B. 2a C. D.
7. 在正方体中,与棱异面的棱的条数为( )
A. 2 B. 4 C. 6 D. 8
8. 如图所示,棱柱的侧面是矩形,D是上的动点,若平面,则的值为 ( )
A. B. C. D. 1
二、多选题(本大题共4小题,共20.0分。在每小题有多项符合题目要求)
9. 若,则下列不等式恒成立的是( )
A. B. C. D.
10. 已知向量,,则下列叙述正确的是( )
A. 若,则 B. 若与的夹角为锐角,则
C. 若,则 D. 与共线的单位向量
11. 如图所示,在正方体中,M,N分别为棱,的中点,其中正确的结论为( )
A. 直线AM与是相交直线 B. 直线 AM与 BN是平行直线
C. 直线 BN与是异面直线 D. 直线MN与AC所成的角为
12. 在中,角A,B,C所对的边分别为a,b,c,已知,则下列结论正确的是( )
A. B.
C. 若,则的面积是15 D. 若,则外接圆半径是
第II卷(非选择题)
三、填空题(本大题共4小题,共20.0分)
13. 若函数为定义在上的偶函数,则__________.
若,,则__________.
已知球O的表面积为,则球O的半径为__________.
一个长方体的长、宽、高分别为9,8,3,若在上面钻一个高为3的贯穿上下表面的圆柱形孔后,其表面积没有变化,则孔的半径为__________.
14. 已知向量,,
设与的夹角为,求的值;
若与平行,求实数t的值.
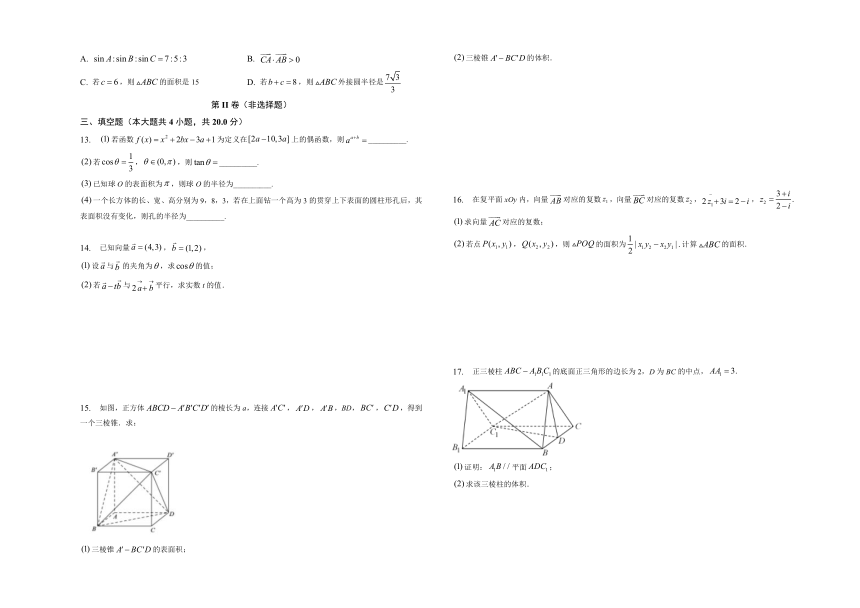
15. 如图,正方体的棱长为a,连接,,,BD,,,得到一个三棱锥.求:
三棱锥的表面积;
三棱锥的体积.
16. 在复平面xOy内,向量对应的复数,向量对应的复数,,
求向量对应的复数;
若点,,则的面积为计算的面积.
17. 正三棱柱的底面正三角形的边长为2,D为BC的中点,
证明:平面;
求该三棱柱的体积.
18. 在中,内角A,B,C的对边分别为a,b,c,且
求角B的大小;
若,,求a,c的值.
19. 如图,四棱锥的底面为平行四边形.设平面PAD与平面PBC的交线为l,M、N、Q分别为PC、CD、AB的中点.
求证:平面平面 PAD ;
求证:
黄州中学(黄冈外校)高一年级数学周测6.1(数学)
答案
1.【答案】B
2.【答案】B
3.【答案】B
4.【答案】C
5.【答案】B
6.【答案】A
7.【答案】B
8.【答案】B
9.【答案】BC
10.【答案】AB
11.【答案】CD
12.【答案】ABD
13.【答案】(1)4;
(2)2;
(3);
(4)3
14.【答案】解:(1)向量,,
则 =4×1+3×2=10,
且||==5,
||==;
设与的夹角为θ,
则cosθ===;
(2)若与平行,
则-t=(2+),
所以,解得t=-.
15.【答案】解:(1)∵是正方体,
∴,
∴三棱锥的表面积为.
(2)三棱锥,,,是完全一样的.
且正方体的体积为,
故.
16.【答案】解:(1)依题意,,即,
则z1=1+2i,
又,
因为,
所以向量对应的复数为:z1+z2=(1+2i)+(1+i)=2+3i.
(2)依题意,,,△POQ的面积S=,
由(1)知,对应的复数为2+3i,即有;对应的复数为1+2i,即有,
所以△ABC的面积为.
17.【答案】(1)证明:连接,设,连接
∵四边形是正三棱柱的侧面,
∴四边形为矩形,
∴是的中点,又为的中点,
∴是的中位线,
∴,
又平面,平面,
∴平面.
(2)因为在正三棱柱中,底面正三角形的边长为2,为的中点,
所以,,
故,
又平面,,
所以正三棱柱的体积
18.【答案】解:(1)由bsinA=acosB及正弦定理得:sinBsinA=sinAcosB,
∵,sinA≠0,
∴sinB=cosB tanB=,
而B∈(0,π),
故B=;
(2)由sinC=2sinA及=,得c=2a,①
又b=3,由余弦定理b2=a2+c2-2accosB,得9=a2+c2-ac,②
由①②得a=,c=2.
19.【答案】证明:(1)M、N分别为PC、CD的中点,MNPD,
又PD平面PAD,MN平面PAD,MN平面PAD,
四边形ABCD是平行四边形,Q、N分别为AB、CD的中点,ADQN,
又AD平面PAD,QN平面PAD,QN平面PAD,
又QNMN=N,QN、MN平面MNQ,平面MNQ平面PAD;
(2)四边形ABCD是平行四边形,BCAD,
又AD平面PAD,BC 平面PAD,BC平面PAD,
又BC平面PBC,平面PAD平面PBC=l,BCl.
2023年黄州中学(黄冈外校)高一第二学期第六次阶段性测试
数学试卷
2023年6月1日 考试范围:第六章-第八章;考试时间:120分钟;联合命题:黄冈袭明卓越教育中心
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
第I卷(选择题)
一、单选题(本大题共8小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1. 已知全集,集合,则( )
A. B. C. D.
2. 若点A在平面内,直线l在平面内,点A不在直线l上,下列用集合表示这些语句的描述中,正确的是( )
A. 且 B. 且 C. 且 D. 且
3. 下列说法中正确的是( )
A. 第一象限角是锐角 B. 钝角是第二象限角
C. 终边相同的角一定相等 D. 不相等的角,它们的终边必不相同
4. i为虚数单位,已知复数是纯虚数,则a等于( )
A. B. 1 C. D. 0
5. 已知向量,,若,则( )
A. B. 1 C. D.
6. 已知侧棱长为2a的正三棱锥底面为等边三角形其底面周长为9a,则棱锥的高为( )
A. a B. 2a C. D.
7. 在正方体中,与棱异面的棱的条数为( )
A. 2 B. 4 C. 6 D. 8
8. 如图所示,棱柱的侧面是矩形,D是上的动点,若平面,则的值为 ( )
A. B. C. D. 1
二、多选题(本大题共4小题,共20.0分。在每小题有多项符合题目要求)
9. 若,则下列不等式恒成立的是( )
A. B. C. D.
10. 已知向量,,则下列叙述正确的是( )
A. 若,则 B. 若与的夹角为锐角,则
C. 若,则 D. 与共线的单位向量
11. 如图所示,在正方体中,M,N分别为棱,的中点,其中正确的结论为( )
A. 直线AM与是相交直线 B. 直线 AM与 BN是平行直线
C. 直线 BN与是异面直线 D. 直线MN与AC所成的角为
12. 在中,角A,B,C所对的边分别为a,b,c,已知,则下列结论正确的是( )
A. B.
C. 若,则的面积是15 D. 若,则外接圆半径是
第II卷(非选择题)
三、填空题(本大题共4小题,共20.0分)
13. 若函数为定义在上的偶函数,则__________.
若,,则__________.
已知球O的表面积为,则球O的半径为__________.
一个长方体的长、宽、高分别为9,8,3,若在上面钻一个高为3的贯穿上下表面的圆柱形孔后,其表面积没有变化,则孔的半径为__________.
14. 已知向量,,
设与的夹角为,求的值;
若与平行,求实数t的值.
15. 如图,正方体的棱长为a,连接,,,BD,,,得到一个三棱锥.求:
三棱锥的表面积;
三棱锥的体积.
16. 在复平面xOy内,向量对应的复数,向量对应的复数,,
求向量对应的复数;
若点,,则的面积为计算的面积.
17. 正三棱柱的底面正三角形的边长为2,D为BC的中点,
证明:平面;
求该三棱柱的体积.
18. 在中,内角A,B,C的对边分别为a,b,c,且
求角B的大小;
若,,求a,c的值.
19. 如图,四棱锥的底面为平行四边形.设平面PAD与平面PBC的交线为l,M、N、Q分别为PC、CD、AB的中点.
求证:平面平面 PAD ;
求证:
黄州中学(黄冈外校)高一年级数学周测6.1(数学)
答案
1.【答案】B
2.【答案】B
3.【答案】B
4.【答案】C
5.【答案】B
6.【答案】A
7.【答案】B
8.【答案】B
9.【答案】BC
10.【答案】AB
11.【答案】CD
12.【答案】ABD
13.【答案】(1)4;
(2)2;
(3);
(4)3
14.【答案】解:(1)向量,,
则 =4×1+3×2=10,
且||==5,
||==;
设与的夹角为θ,
则cosθ===;
(2)若与平行,
则-t=(2+),
所以,解得t=-.
15.【答案】解:(1)∵是正方体,
∴,
∴三棱锥的表面积为.
(2)三棱锥,,,是完全一样的.
且正方体的体积为,
故.
16.【答案】解:(1)依题意,,即,
则z1=1+2i,
又,
因为,
所以向量对应的复数为:z1+z2=(1+2i)+(1+i)=2+3i.
(2)依题意,,,△POQ的面积S=,
由(1)知,对应的复数为2+3i,即有;对应的复数为1+2i,即有,
所以△ABC的面积为.
17.【答案】(1)证明:连接,设,连接
∵四边形是正三棱柱的侧面,
∴四边形为矩形,
∴是的中点,又为的中点,
∴是的中位线,
∴,
又平面,平面,
∴平面.
(2)因为在正三棱柱中,底面正三角形的边长为2,为的中点,
所以,,
故,
又平面,,
所以正三棱柱的体积
18.【答案】解:(1)由bsinA=acosB及正弦定理得:sinBsinA=sinAcosB,
∵,sinA≠0,
∴sinB=cosB tanB=,
而B∈(0,π),
故B=;
(2)由sinC=2sinA及=,得c=2a,①
又b=3,由余弦定理b2=a2+c2-2accosB,得9=a2+c2-ac,②
由①②得a=,c=2.
19.【答案】证明:(1)M、N分别为PC、CD的中点,MNPD,
又PD平面PAD,MN平面PAD,MN平面PAD,
四边形ABCD是平行四边形,Q、N分别为AB、CD的中点,ADQN,
又AD平面PAD,QN平面PAD,QN平面PAD,
又QNMN=N,QN、MN平面MNQ,平面MNQ平面PAD;
(2)四边形ABCD是平行四边形,BCAD,
又AD平面PAD,BC 平面PAD,BC平面PAD,
又BC平面PBC,平面PAD平面PBC=l,BCl.
同课章节目录
