湖北省黄冈市黄州中学(黄冈外校)2022-2023学年高一下学期实验朝阳班第六次阶段性测试数学试卷(含答案)
文档属性
| 名称 | 湖北省黄冈市黄州中学(黄冈外校)2022-2023学年高一下学期实验朝阳班第六次阶段性测试数学试卷(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 798.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-08 00:00:00 | ||
图片预览

文档简介
机密★启用前
2023年湖北省黄州中学(黄冈外校)高一第二学期实验朝阳班第六次阶段性测试
数学试卷
2023年6月1日 考试范围:第六章-第八章;考试时间:120分钟;联合命题:黄冈袭明卓越教育中心
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
第I卷(选择题)
一、单选题(本大题共8小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1. 已知i是虚数单位,复数z满足,则复数z的共轭复数虚部为( )
A. B. C. D.
2. 已知是两条不重合的直线,是两个不重合的平面,下列命题正确的是( )
A. 若,则 B. 若,则
C. 若,则 D. 若,则
3. 已知二面角的大小为,b和c是两条异面直线,且,则b与c所成的角的大小为( )
A. B. C. D.
4. 如图1,在高为h的直三棱柱容器中,现往该容器内灌进一些水,水深为2,然后固定容器底面的一边AB于地面上,再将容器倾斜,当倾斜到某一位置时,水面恰为如图,则容器的体积为( )
A. B. 3 C. D. 6
5. 已知外接圆的半径为1,圆心为若,且,则等于( )
A. B. C. D. 3
6. 若,,,,则( )
A. B. C. D.
7. 正四棱台上、下底边长为、,外接球表面积为,则正四棱台侧棱与底面所成角的正切值为( )
A. 1 B. 3 C. 1或3 D. 或
8. 在锐角中,角的对边分别为,且满足若恒成立,则实数的取值范围为( )
A. B. C. D.
二、多选题(本大题共4小题,共20.0分。在每小题有多项符合题目要求)
9. 在中,已知,,,则角A的值可能为( )
A. B. C. D.
10. 下列论断中,正确的有( )
A. 在中,若A为钝角,则
B. 在中,角的对边分别为,若,则为等腰三角形
C. 已知向量是非零向量,则向量与向量共线存在不全为零的实数,使
D. 向量 满足,则或
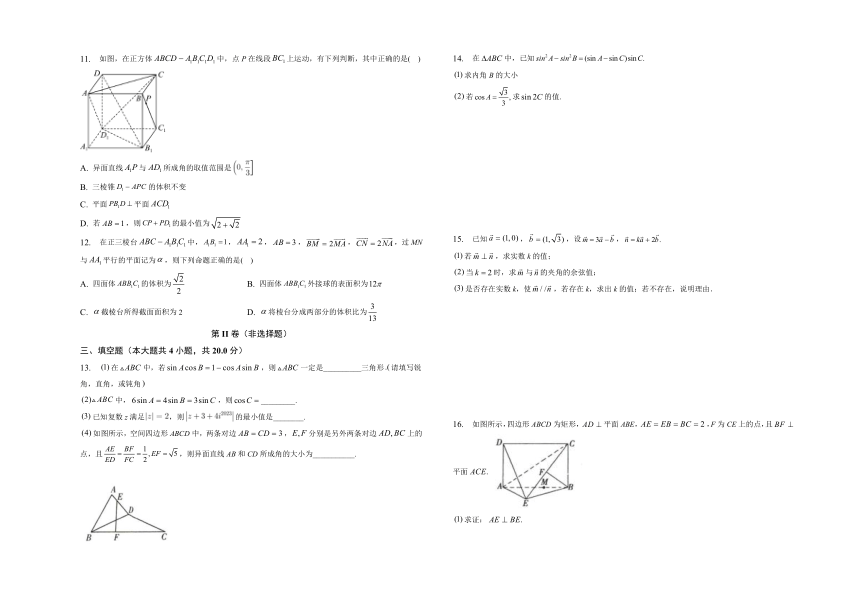
11. 如图,在正方体中,点P在线段上运动,有下列判断,其中正确的是( )
A. 异面直线与所成角的取值范围是
B. 三棱锥的体积不变
C. 平面平面
D. 若,则的最小值为
12. 在正三棱台中,,,,,,过MN与平行的平面记为,则下列命题正确的是( )
A. 四面体的体积为 B. 四面体外接球的表面积为
C. 截棱台所得截面面积为2 D. 将棱台分成两部分的体积比为
第II卷(非选择题)
三、填空题(本大题共4小题,共20.0分)
13. 在中,若,则一定是__________三角形请填写锐角,直角,或钝角
中,,则_________.
已知复数z满足,则的最小值是________.
如图所示,空间四边形ABCD中,两条对边,分别是另外两条对边上的点,且,则异面直线AB和CD所成角的大小为___________.
14. 在中,已知
求内角B的大小
若求的值.
15. 已知,,设,
若,求实数k的值;
当时,求与的夹角的余弦值;
是否存在实数k,使,若存在k,求出k的值;若不存在,说明理由.
16. 如图所示,四边形ABCD为矩形,平面ABE,,F为CE上的点,且平面
求证:
若点M在线段AB上,且满足,则线段CE上是否存在一点N,使得平面ADE?若存在,求出点N的位置;若不存在,请说明理由.
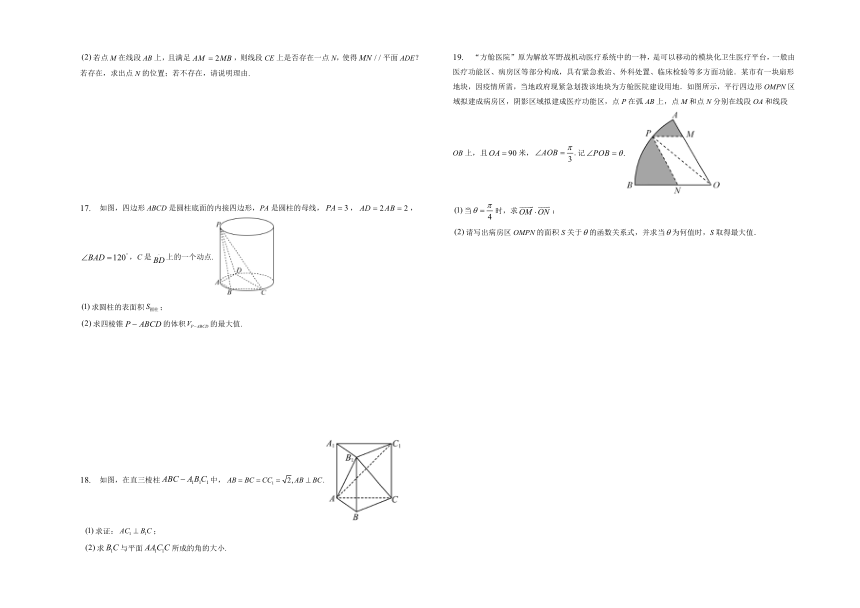
17. 如图,四边形ABCD是圆柱底面的内接四边形,PA是圆柱的母线,,,,C是上的一个动点.
求圆柱的表面积;
求四棱锥的体积的最大值.
18. 如图,在直三棱柱中,
求证:;
求与平面所成的角的大小.
19. “方舱医院”原为解放军野战机动医疗系统中的一种,是可以移动的模块化卫生医疗平台,一般由医疗功能区、病房区等部分构成,具有紧急救治、外科处置、临床检验等多方面功能.某市有一块扇形地块,因疫情所需,当地政府现紧急划拨该地块为方舱医院建设用地.如图所示,平行四边形OMPN区域拟建成病房区,阴影区域拟建成医疗功能区,点P在弧AB上,点M和点N分别在线段OA和线段OB上,且米,记
当时,求;
请写出病房区OMPN的面积S关于的函数关系式,并求当为何值时,S取得最大值.
黄州中学(黄冈外校)高一朝阳班数学测试6.1(数学)
答案
1.【答案】B
2.【答案】D
3.【答案】C
4.【答案】D
5.【答案】D
6.【答案】C
7.【答案】C
8.【答案】B
9.【答案】BC
10.【答案】AC
11.【答案】BCD
12.【答案】ABC
13.【答案】(1)直角
(2)
(3)3
(4)90°
14.【答案】解:(1)在中,设角,,的对边分别为,,,
由正弦定理
及得,
,即,
由余弦定理得,
因为,所以.
(2)因为在中,,
所以,
所以,
,
而,
所以
.
15.【答案】解:(1)由题意,向量 , ,可得 ,
由⊥,得=
=3k+6-k-8=0,解得k=1;
(2)k=2时,=,
=,
=6+4-8=2.
∴cos<>=,
∴与的夹角的余弦值为;
(3)由∥,则成立,得(λ≠0),
因为不共线,故,解得.
∴存在实数k=-6,使得∥.
16.【答案】(1)证明:∵AD⊥平面ABE,AD∥BC,∴BC⊥平面ABE.
又AE 平面ABE,∴AE⊥BC.
∵BF⊥平面ACE,AE 平面ACE,∴AE⊥BF.
又BC∩BF=B,BC,BF都在平面BCE内,∴AE⊥平面BCE.
又BE 平面BCE,∴AE⊥BE.
(2)存在满足题意得点N.
如图所示,在△ABE中,过点M作MG∥AE交BE于点G,
在△BEC中,过点G作GN∥BC交EC于点N,连接MN,
则由比例关系,易得CN=CE.
∵MG∥AE,MG 平面ADE,AE 平面ADE,
∴MG∥平面ADE,
∵GN∥BC,BC∥AD,GN 平面ADE,AD 平面ADE,
∴GN∥平面ADE,
又GN∩MG,GN,MG都在平面MGN内,∴平面MGN∥平面ADE,
又MN 平面MGN,∴MN∥平面ADE,
∴点N为线段CE上靠近点C的三等分点.
17.【答案】解:(1)连接BD,在 中, , , ,
由余弦定理,得 ,
所以 ,设圆柱底面半径为r,
由正弦定理,得 ,
所以 ,故圆柱的表面积 .
(2)由(1)知, 中, , ,
由余弦定理,得
,
即 ,当且仅当 时,等号成立,
所以 ,
因为 , ,
所以四棱锥 的体积,
,
故四棱锥 的体积 的最大值为 .
18.【答案】(1)证明: 连接与C相交于点D,
直棱柱ABC-中,面ABC,AB 面ABC,
AB,
又ABBC,BC=B,BC,面C,
AB面C,又C面C,
ABC
BC=,
四边形为菱形,
即C
又AB=D,且AB,面,
C面
又面,
C.
(2)解:取的中点E,连接E,CE.
=,E=,
E,
又面A1B1C1,E面A1B1C1,
E,
又=,且,面C,
E面C,
CE是在面C内的射影,是与平面C所成的角.
在RT中,E=1,=2,
==,
=
与平面C所成的角的大小为.
19.【答案】解:(1)根据题意,在OPM中,
MOP=,PMO=,MPO=,
又OP=90,
sin=sin(-)
=sincos-cossin=,
故由正弦定理==,
可得:==,
解得PM=ON=45(-),OM=30,
=OMONAOB
=3045(-)=1350(-1)
即=1350(-1);
(2)由题可知,在PMO中,OP=90,PMO=,MPO=,MOP=-,
则由正弦定理==,
可得==,
故OM=60,PM=60(-),
=PMOMPMO
=60(-)60
=2700(-)=2700(-)
=2700(2+2-)
=2700[(2+)-]
=1350(2+)-675,(0<<)
即S==2700(2+)-1350,(0<<)
显然 ,因此当 ,即 时, , 取得最大值,
所以 ,当 时, 取得最大值.
当=时,(2+)=1,此时S取得最大值.
2023年湖北省黄州中学(黄冈外校)高一第二学期实验朝阳班第六次阶段性测试
数学试卷
2023年6月1日 考试范围:第六章-第八章;考试时间:120分钟;联合命题:黄冈袭明卓越教育中心
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
第I卷(选择题)
一、单选题(本大题共8小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1. 已知i是虚数单位,复数z满足,则复数z的共轭复数虚部为( )
A. B. C. D.
2. 已知是两条不重合的直线,是两个不重合的平面,下列命题正确的是( )
A. 若,则 B. 若,则
C. 若,则 D. 若,则
3. 已知二面角的大小为,b和c是两条异面直线,且,则b与c所成的角的大小为( )
A. B. C. D.
4. 如图1,在高为h的直三棱柱容器中,现往该容器内灌进一些水,水深为2,然后固定容器底面的一边AB于地面上,再将容器倾斜,当倾斜到某一位置时,水面恰为如图,则容器的体积为( )
A. B. 3 C. D. 6
5. 已知外接圆的半径为1,圆心为若,且,则等于( )
A. B. C. D. 3
6. 若,,,,则( )
A. B. C. D.
7. 正四棱台上、下底边长为、,外接球表面积为,则正四棱台侧棱与底面所成角的正切值为( )
A. 1 B. 3 C. 1或3 D. 或
8. 在锐角中,角的对边分别为,且满足若恒成立,则实数的取值范围为( )
A. B. C. D.
二、多选题(本大题共4小题,共20.0分。在每小题有多项符合题目要求)
9. 在中,已知,,,则角A的值可能为( )
A. B. C. D.
10. 下列论断中,正确的有( )
A. 在中,若A为钝角,则
B. 在中,角的对边分别为,若,则为等腰三角形
C. 已知向量是非零向量,则向量与向量共线存在不全为零的实数,使
D. 向量 满足,则或
11. 如图,在正方体中,点P在线段上运动,有下列判断,其中正确的是( )
A. 异面直线与所成角的取值范围是
B. 三棱锥的体积不变
C. 平面平面
D. 若,则的最小值为
12. 在正三棱台中,,,,,,过MN与平行的平面记为,则下列命题正确的是( )
A. 四面体的体积为 B. 四面体外接球的表面积为
C. 截棱台所得截面面积为2 D. 将棱台分成两部分的体积比为
第II卷(非选择题)
三、填空题(本大题共4小题,共20.0分)
13. 在中,若,则一定是__________三角形请填写锐角,直角,或钝角
中,,则_________.
已知复数z满足,则的最小值是________.
如图所示,空间四边形ABCD中,两条对边,分别是另外两条对边上的点,且,则异面直线AB和CD所成角的大小为___________.
14. 在中,已知
求内角B的大小
若求的值.
15. 已知,,设,
若,求实数k的值;
当时,求与的夹角的余弦值;
是否存在实数k,使,若存在k,求出k的值;若不存在,说明理由.
16. 如图所示,四边形ABCD为矩形,平面ABE,,F为CE上的点,且平面
求证:
若点M在线段AB上,且满足,则线段CE上是否存在一点N,使得平面ADE?若存在,求出点N的位置;若不存在,请说明理由.
17. 如图,四边形ABCD是圆柱底面的内接四边形,PA是圆柱的母线,,,,C是上的一个动点.
求圆柱的表面积;
求四棱锥的体积的最大值.
18. 如图,在直三棱柱中,
求证:;
求与平面所成的角的大小.
19. “方舱医院”原为解放军野战机动医疗系统中的一种,是可以移动的模块化卫生医疗平台,一般由医疗功能区、病房区等部分构成,具有紧急救治、外科处置、临床检验等多方面功能.某市有一块扇形地块,因疫情所需,当地政府现紧急划拨该地块为方舱医院建设用地.如图所示,平行四边形OMPN区域拟建成病房区,阴影区域拟建成医疗功能区,点P在弧AB上,点M和点N分别在线段OA和线段OB上,且米,记
当时,求;
请写出病房区OMPN的面积S关于的函数关系式,并求当为何值时,S取得最大值.
黄州中学(黄冈外校)高一朝阳班数学测试6.1(数学)
答案
1.【答案】B
2.【答案】D
3.【答案】C
4.【答案】D
5.【答案】D
6.【答案】C
7.【答案】C
8.【答案】B
9.【答案】BC
10.【答案】AC
11.【答案】BCD
12.【答案】ABC
13.【答案】(1)直角
(2)
(3)3
(4)90°
14.【答案】解:(1)在中,设角,,的对边分别为,,,
由正弦定理
及得,
,即,
由余弦定理得,
因为,所以.
(2)因为在中,,
所以,
所以,
,
而,
所以
.
15.【答案】解:(1)由题意,向量 , ,可得 ,
由⊥,得=
=3k+6-k-8=0,解得k=1;
(2)k=2时,=,
=,
=6+4-8=2.
∴cos<>=,
∴与的夹角的余弦值为;
(3)由∥,则成立,得(λ≠0),
因为不共线,故,解得.
∴存在实数k=-6,使得∥.
16.【答案】(1)证明:∵AD⊥平面ABE,AD∥BC,∴BC⊥平面ABE.
又AE 平面ABE,∴AE⊥BC.
∵BF⊥平面ACE,AE 平面ACE,∴AE⊥BF.
又BC∩BF=B,BC,BF都在平面BCE内,∴AE⊥平面BCE.
又BE 平面BCE,∴AE⊥BE.
(2)存在满足题意得点N.
如图所示,在△ABE中,过点M作MG∥AE交BE于点G,
在△BEC中,过点G作GN∥BC交EC于点N,连接MN,
则由比例关系,易得CN=CE.
∵MG∥AE,MG 平面ADE,AE 平面ADE,
∴MG∥平面ADE,
∵GN∥BC,BC∥AD,GN 平面ADE,AD 平面ADE,
∴GN∥平面ADE,
又GN∩MG,GN,MG都在平面MGN内,∴平面MGN∥平面ADE,
又MN 平面MGN,∴MN∥平面ADE,
∴点N为线段CE上靠近点C的三等分点.
17.【答案】解:(1)连接BD,在 中, , , ,
由余弦定理,得 ,
所以 ,设圆柱底面半径为r,
由正弦定理,得 ,
所以 ,故圆柱的表面积 .
(2)由(1)知, 中, , ,
由余弦定理,得
,
即 ,当且仅当 时,等号成立,
所以 ,
因为 , ,
所以四棱锥 的体积,
,
故四棱锥 的体积 的最大值为 .
18.【答案】(1)证明: 连接与C相交于点D,
直棱柱ABC-中,面ABC,AB 面ABC,
AB,
又ABBC,BC=B,BC,面C,
AB面C,又C面C,
ABC
BC=,
四边形为菱形,
即C
又AB=D,且AB,面,
C面
又面,
C.
(2)解:取的中点E,连接E,CE.
=,E=,
E,
又面A1B1C1,E面A1B1C1,
E,
又=,且,面C,
E面C,
CE是在面C内的射影,是与平面C所成的角.
在RT中,E=1,=2,
==,
=
与平面C所成的角的大小为.
19.【答案】解:(1)根据题意,在OPM中,
MOP=,PMO=,MPO=,
又OP=90,
sin=sin(-)
=sincos-cossin=,
故由正弦定理==,
可得:==,
解得PM=ON=45(-),OM=30,
=OMONAOB
=3045(-)=1350(-1)
即=1350(-1);
(2)由题可知,在PMO中,OP=90,PMO=,MPO=,MOP=-,
则由正弦定理==,
可得==,
故OM=60,PM=60(-),
=PMOMPMO
=60(-)60
=2700(-)=2700(-)
=2700(2+2-)
=2700[(2+)-]
=1350(2+)-675,(0<<)
即S==2700(2+)-1350,(0<<)
显然 ,因此当 ,即 时, , 取得最大值,
所以 ,当 时, 取得最大值.
当=时,(2+)=1,此时S取得最大值.
同课章节目录
