三角形的中位线[下学期]
图片预览




文档简介
课件23张PPT。三角形的中位线 课前热身------折纸游戏你能做到吗?
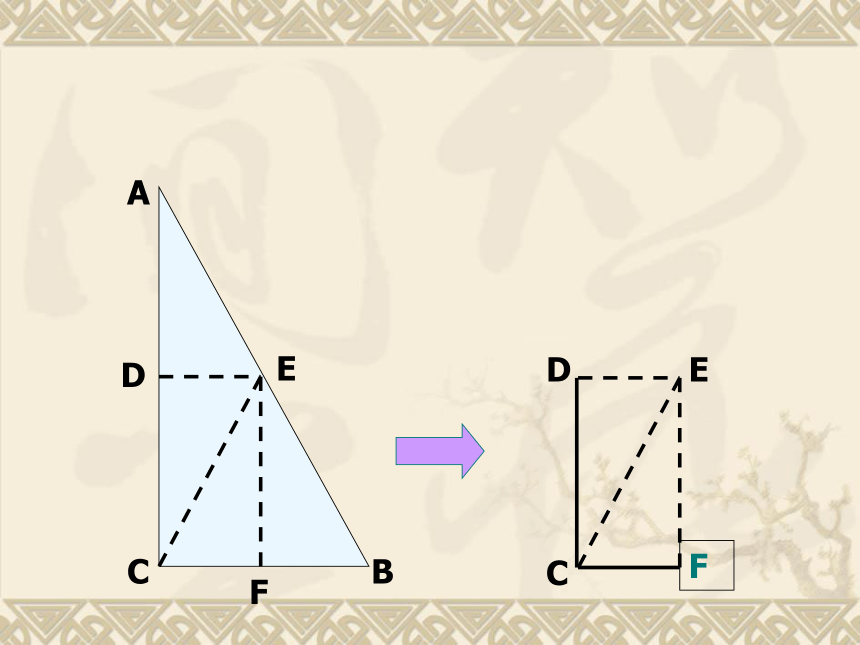
1. 用一张直角三角形形状的纸片,你能折叠成面积减半的长方形吗?课前热身------折纸游戏
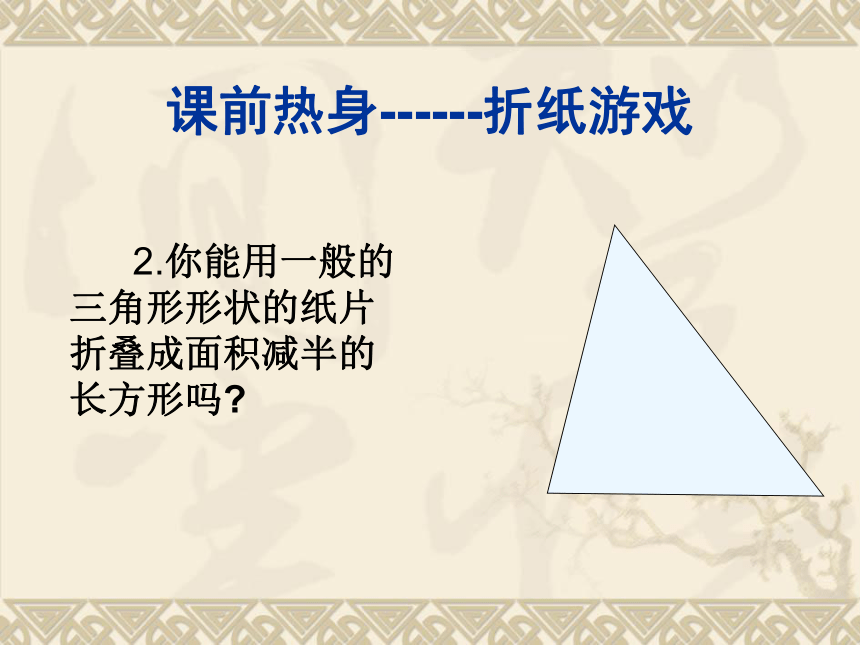
2.你能用一般的三角形形状的纸片折叠成面积减半的长方形吗? 观察图中的折痕DE,你发现它有什么特点吗?观察与发现AB问题:A、B两点被池塘隔开,如何测量A、B两点距离呢?为什么?
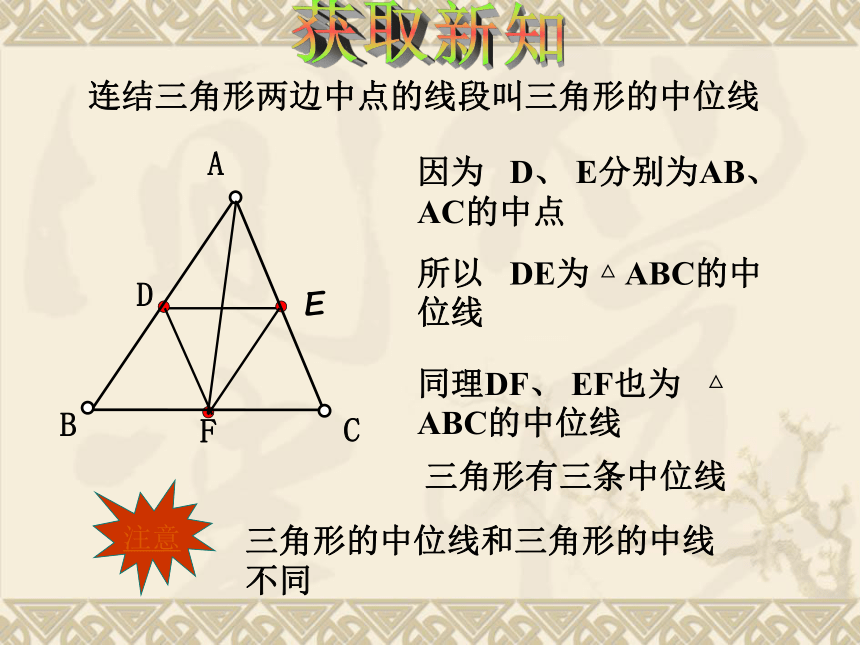
获取新知连结三角形两边中点的线段叫三角形的中位线三角形有三条中位线因为 D、 E分别为AB、 AC的中点
所以 DE为 △ ABC的中位线
三角形的中位线和三角形的中线不同同理DF、 EF也为 △ ABC的中位线
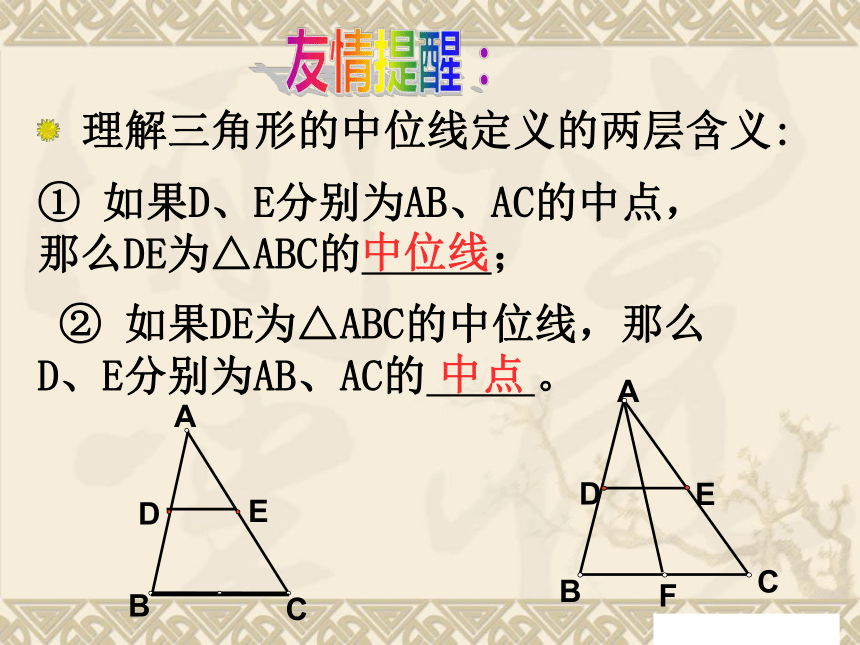
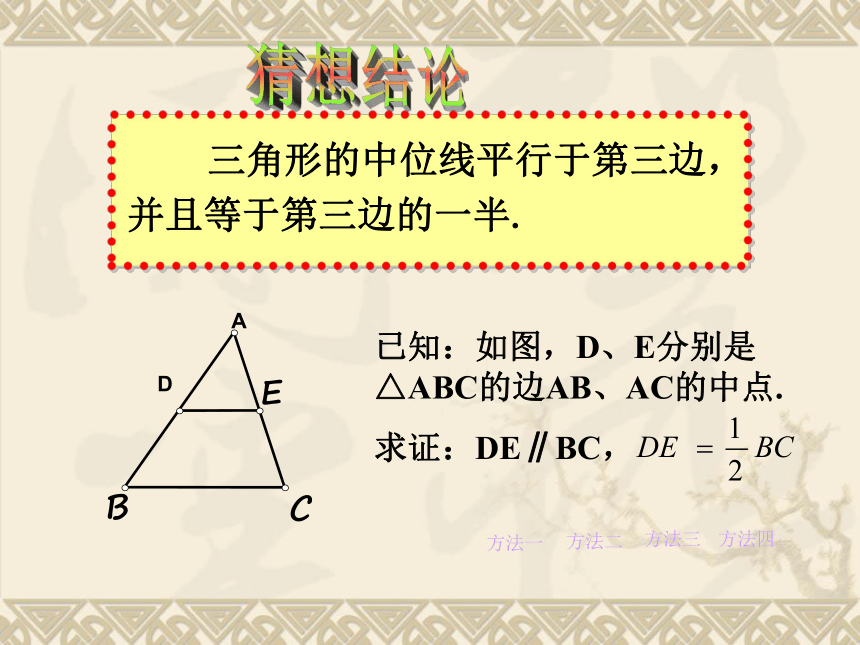
EDF友情提醒: 理解三角形的中位线定义的两层含义: ② 如果DE为△ABC的中位线,那么 D、E分别为AB、AC的 。① 如果D、E分别为AB、AC的中点, 那么DE为△ABC的 ;CBAED中位线中点猜想结论 三角形的中位线平行于第三边,并且等于第三边的一半.已知:如图,D、E分别是△ABC的边AB、AC的中点.
求证:DE∥BC,方法二方法三方法一方法四A三角形中位线定理 三角形的中位线平行于第三边,并且等于第三边的一半.几何语言:∵DE是△ABC的中位线(或AD=BD,AE=CE)
∴DE∥BC,且DE= BC
(三角形的中位线平行于第三边,并且等于它的一半)
方法点拨:
在处理问题时,要求同时出现三角形及中位线
①有中点连线而无三角形,要作辅助线产生三角形
②有三角形而无中位线,要连结两边中点得中位线定 理 应 用:⑴定理为证明平行关系提供了新的工具
⑵定理为证明一条线段是另一条线段的2倍或 提供了一个新的途径若DE分别是AB,AC的中点,则测出DE的长,就可以求出池塘的宽BC.你知道为什么吗?1.△ABC中,D、E分别是AB、AC的中点,
BC=10cm,则DE=______.
2. △ABC中,D、E分别是AB、AC的中点,
∠A=50°, ∠B=70°,则∠AED=_____.AEDCB(1)AEDBC(2)新知应用初显身手△ABC中所有的中位线 三条中位线围成一个新的三角形,它与原来的三角形有无关系?哪方面有关系?(1) △DEF的周长与 △ABC的周长有什么关系?(2) △DEF的面积与 △ABC的面积有什么关系?探索研究: 已知:△ABC的周长为a,面积为s,连接各边中点得△A1B1C1,再连接△A1B1C1各边中点得△A2B2C2 ……,
则(1) 第3次连接所得
△A3B3C3的周长=____,面积=____
(2)第n次连接所得
△AnBnCn的周长=____,面积=____ ABCA1B1C1
A2B2C2分析:填表例1 求证三角形的一条中位线与第三边上的中线互相平分。
已知:如图,在△ABC中,AD=DB,BE=EC,AF=FC
求证:AE、DF互相平分例3、如图:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,四边形EFGH是什么四边形?为什么?结论: 顺次连结四边形各边中点所得四边形是平行四边形。中点四边形3.已知:如图,在四边形ABCD中,E,F,G,H分
别是边AB,CD,AC,BD的中点.
求证:四边形EGFH是平行四边形.菱形矩形正方形用平行四边形、矩形、菱形、正方形填空。
1.顺次连结平行四边形各边中点所得的四边形是
2.顺次连结矩形各边中点所得的四边形是
3.顺次连结菱形各边中点所得的四边形是
4.顺次连结正方形各边中点所得的四边形是
5.顺次连结等腰梯形各边中点所得的四边形是平行四边形菱形矩形正方形菱形结论:原四边形中点四边形对角线相等对角线垂直对角线垂直、相等对角线既不相等也不垂直平行四边形 顺次连接四边形各边中点所得到的四边形一定是平行四边形,但它是否特殊的平行四边形取决于什么呢?议一议课堂训练 练一练:1。如图(1)ΔABC中,
AB=6㎝, AC=8㎝,BC=10㎝,
D﹑E﹑F分别是ABACBC的中点
则ΔDEF的周长是____ ,
面积是____。 2.如图(2)ΔABC中,DE是
中位线,AF是中线,则DE与
AF的关系是____3.若顺次连接四边形四边中
点所得的四边形是菱形,则
原四边形( )
(A)一定是矩形 (B)一定是菱形
(C)对角线一定互相垂直 (D)对角线一定相等
FACBDEF(2)互相平分6cm212cmD这节课我们学了: 1.三角形中位线的概念:连接三角形两边的中点的线段叫做三角形的中位线。
2.三角形中位线的性质:三角形的中位线平行与第三边,并且等于它的一半。
3.应用三角形中位线的性质解决有关计算或说理等问题。再见
1. 用一张直角三角形形状的纸片,你能折叠成面积减半的长方形吗?课前热身------折纸游戏
2.你能用一般的三角形形状的纸片折叠成面积减半的长方形吗? 观察图中的折痕DE,你发现它有什么特点吗?观察与发现AB问题:A、B两点被池塘隔开,如何测量A、B两点距离呢?为什么?
获取新知连结三角形两边中点的线段叫三角形的中位线三角形有三条中位线因为 D、 E分别为AB、 AC的中点
所以 DE为 △ ABC的中位线
三角形的中位线和三角形的中线不同同理DF、 EF也为 △ ABC的中位线
EDF友情提醒: 理解三角形的中位线定义的两层含义: ② 如果DE为△ABC的中位线,那么 D、E分别为AB、AC的 。① 如果D、E分别为AB、AC的中点, 那么DE为△ABC的 ;CBAED中位线中点猜想结论 三角形的中位线平行于第三边,并且等于第三边的一半.已知:如图,D、E分别是△ABC的边AB、AC的中点.
求证:DE∥BC,方法二方法三方法一方法四A三角形中位线定理 三角形的中位线平行于第三边,并且等于第三边的一半.几何语言:∵DE是△ABC的中位线(或AD=BD,AE=CE)
∴DE∥BC,且DE= BC
(三角形的中位线平行于第三边,并且等于它的一半)
方法点拨:
在处理问题时,要求同时出现三角形及中位线
①有中点连线而无三角形,要作辅助线产生三角形
②有三角形而无中位线,要连结两边中点得中位线定 理 应 用:⑴定理为证明平行关系提供了新的工具
⑵定理为证明一条线段是另一条线段的2倍或 提供了一个新的途径若DE分别是AB,AC的中点,则测出DE的长,就可以求出池塘的宽BC.你知道为什么吗?1.△ABC中,D、E分别是AB、AC的中点,
BC=10cm,则DE=______.
2. △ABC中,D、E分别是AB、AC的中点,
∠A=50°, ∠B=70°,则∠AED=_____.AEDCB(1)AEDBC(2)新知应用初显身手△ABC中所有的中位线 三条中位线围成一个新的三角形,它与原来的三角形有无关系?哪方面有关系?(1) △DEF的周长与 △ABC的周长有什么关系?(2) △DEF的面积与 △ABC的面积有什么关系?探索研究: 已知:△ABC的周长为a,面积为s,连接各边中点得△A1B1C1,再连接△A1B1C1各边中点得△A2B2C2 ……,
则(1) 第3次连接所得
△A3B3C3的周长=____,面积=____
(2)第n次连接所得
△AnBnCn的周长=____,面积=____ ABCA1B1C1
A2B2C2分析:填表例1 求证三角形的一条中位线与第三边上的中线互相平分。
已知:如图,在△ABC中,AD=DB,BE=EC,AF=FC
求证:AE、DF互相平分例3、如图:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,四边形EFGH是什么四边形?为什么?结论: 顺次连结四边形各边中点所得四边形是平行四边形。中点四边形3.已知:如图,在四边形ABCD中,E,F,G,H分
别是边AB,CD,AC,BD的中点.
求证:四边形EGFH是平行四边形.菱形矩形正方形用平行四边形、矩形、菱形、正方形填空。
1.顺次连结平行四边形各边中点所得的四边形是
2.顺次连结矩形各边中点所得的四边形是
3.顺次连结菱形各边中点所得的四边形是
4.顺次连结正方形各边中点所得的四边形是
5.顺次连结等腰梯形各边中点所得的四边形是平行四边形菱形矩形正方形菱形结论:原四边形中点四边形对角线相等对角线垂直对角线垂直、相等对角线既不相等也不垂直平行四边形 顺次连接四边形各边中点所得到的四边形一定是平行四边形,但它是否特殊的平行四边形取决于什么呢?议一议课堂训练 练一练:1。如图(1)ΔABC中,
AB=6㎝, AC=8㎝,BC=10㎝,
D﹑E﹑F分别是ABACBC的中点
则ΔDEF的周长是____ ,
面积是____。 2.如图(2)ΔABC中,DE是
中位线,AF是中线,则DE与
AF的关系是____3.若顺次连接四边形四边中
点所得的四边形是菱形,则
原四边形( )
(A)一定是矩形 (B)一定是菱形
(C)对角线一定互相垂直 (D)对角线一定相等
FACBDEF(2)互相平分6cm212cmD这节课我们学了: 1.三角形中位线的概念:连接三角形两边的中点的线段叫做三角形的中位线。
2.三角形中位线的性质:三角形的中位线平行与第三边,并且等于它的一半。
3.应用三角形中位线的性质解决有关计算或说理等问题。再见
同课章节目录
