图形的相似复习课件

课件12张PPT。 图形的相似
（复 习 课）2018/12/27复习要求 考查角度
1．了解相似多边形、相似比和相似三角形的概念，掌握其性质和判定并会运用图形的相似解决一些简单的实际问题．
2．了解位似变换和位似图形的概念，掌握并运用其性质. 　　
3.相似多边形的性质是重点，其中以相似多边形的相似比、面积比、周长比的关系考查较多．相似三角形的判定、性质及应用是考查的重点。3问题1：何谓相似形？ 相似形是指形状相同，大小不一定相等两个图形。
问题3：何谓相似三角形？如何判定？
定义：三个对应相等，三条对应边成比例的两个三角形
判定方法：1、有两个角相等的两个三角形相似。 2、两边对应成比例，并且夹角相等的两个三角形相似。3、三边对应成比例的两个三角形相似。 问题2：任意两个多边形具备什么条件时它们相似 呢？
只有在对应边都对应成比例，对应角都对应相等时它们相似
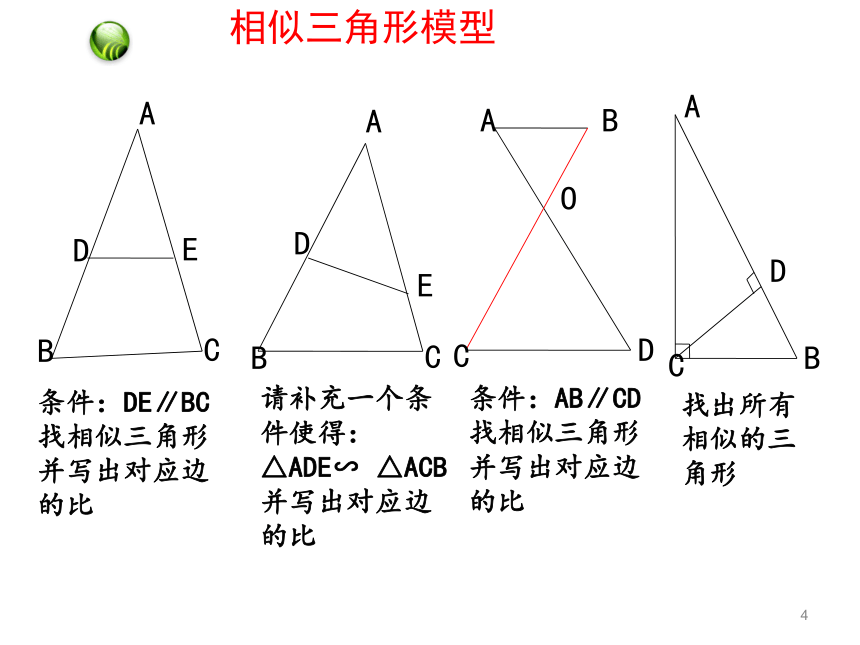
4相似三角形模型条件：DE∥BC
找相似三角形并写出对应边的比条件：AB∥CD
找相似三角形并写出对应边的比
请补充一个条件使得：
△ADE∽ △ACB
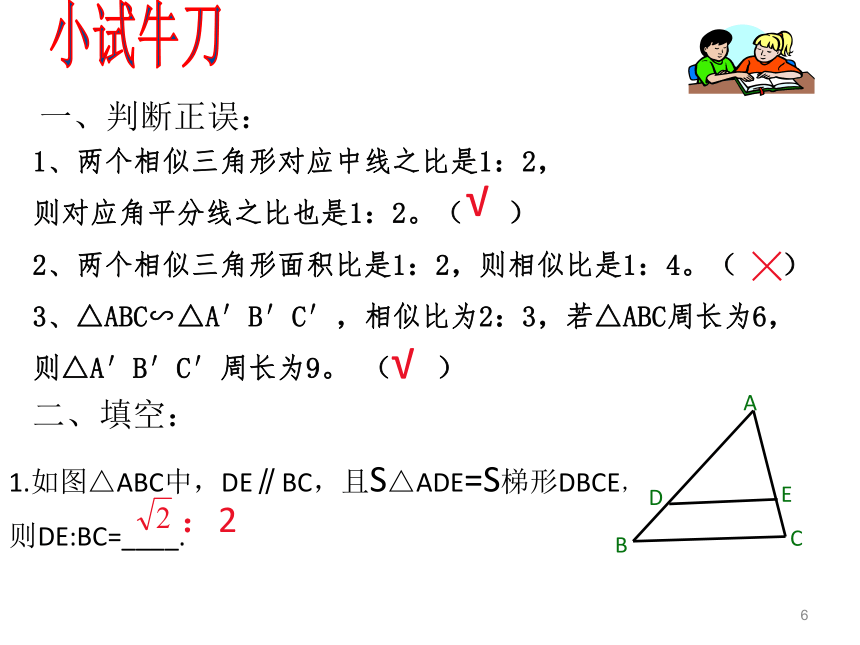
并写出对应边的比找出所有相似的三角形问题4：两个三角形相似时，有哪些性质呢？ ①相似三角形对应边_____，对应角_____ ②相似三角形对应边上中线的比等于_______ ⑥相似三角形面积的比等于___________。③相似三角形对应边上高的比等于_____④相似三角形对应角的角平分线的比等于______⑤相似三角形周长的比等于_______61、两个相似三角形对应中线之比是1：2，
则对应角平分线之比也是1：2。（ ）
2、两个相似三角形面积比是1：2，则相似比是1：4。（ ）
3、△ABC∽△A′B′C′，相似比为2：3，若△ABC周长为6，
则△A′B′C′周长为9。 （ ）二、填空：1.如图△ABC中，DE∥BC，且S△ADE=S梯形DBCE，
则DE:BC=____.一、判断正误：小试牛刀√×√：22018/12/27三、相似图形的特例图形的位似1.如果两个图形不仅相似,而且每组对应顶点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比.2．画位似图形的步骤
(1)确定位似________；
(2)连接图形各顶点与位似中心的线段(或延长线)；
(3)按位似比进行取点；
(4)顺次连接各点，所得的图形就是所求图形2018/12/27如图，在直角坐标系中，矩形OABC的顶点O在坐标原点，边OA在x轴上，OC在y轴上，如果矩形OA′B′C′与矩形OABC关于点O位似，且矩形OA′B′C′的面积等于矩形OABC面积的1/4，那么点B′的坐标是(　　)A．(3,2) B．(－2，－3 ) C．(2,3)或(－2，－3) D．(3,2)或(－3，－2)
9如图, 在△ABC中,AB=5,AC=4,E是AB上一点,AE=2,
在AC上取一点F,使以A、E、F为顶点的三角形与
△ABC相似,那么AF=________如图, 在直角梯形中, ∠BAD=∠D=∠ACB=90。，
CD= 4, AB= 9, 则 AC=______6复习检测（3/8）2018/12/277.如图所示,在△ABC中,底边BC=60cm,高 AD=40cm,四边形PQRS是正方形.
(1)△ASR与△ABC相似吗?为什么?
(2)求正方形PQRS的边长. 本节课主要是复习相似三角形的性质
判定及其运用。在解题中要熟悉基本图
形。并能从条件和结论两方面同时考虑问
题。灵活应用。 回顾与反思12同学们
再见！