湖北省黄冈市黄州中学(黄冈外校)2022-2023学年高一下学期6月阶段性测试数学试题(含答案)
文档属性
| 名称 | 湖北省黄冈市黄州中学(黄冈外校)2022-2023学年高一下学期6月阶段性测试数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 679.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-08 16:07:08 | ||
图片预览


文档简介
机密★启用前
黄州中学(黄冈外校)2022-2023学年高一下学期6月阶段性测试
数学试卷
2023年5月26日 考试范围:第六章-第八章;考试时间:120分钟;联合命题:黄冈袭明卓越教育中心
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
第I卷(选择题)
一、单选题(本大题共8小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1. 在复平面内,复数对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 已知圆台的上下底面圆的半径分别为1与2,高为,则圆台的侧面积为( )
A. B. C. D.
3. 正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( )
A. B. C. D.
4. 已知函数的图象关于点对称,则( )
A. B. C. D.
5. 函数,,则下列结论正确的是( )
A. 是偶函数 B. 是奇函数 C. 是奇函数 D. 是奇函数
6. 如图,已知平面四边形ABCD,,,,AC与BD交于点 O,记,,,则( )
A. B. C. D.
7. 如图所示,在空间四边形ABCD中,E,F分别为AB,AD的中点,分别在,CD上,且则下面几个说法中正确的个数是( )
①E,E,G,H四点共面; ②③若直线EG与直线FH交于点P,则P,A,C三点共线.
A. 0 B. 1 C. 2 D. 3
8. 如图,正方体的棱长为6,P为BC的中点,Q为的中点, 过点,P,Q的平面截正方体所得的截面的面积( )
A. B. C. D.
二、多选题(本大题共4小题,共20.0分。在每小题有多项符合题目要求)
9. 设a,b是两条不重合的直线,,是两个不同的平面.下列四个命题中,正确的是( )
A. 若,,则 B. 若,,则
C. 若,,则 D. 若,,则
10. 已知圆锥的母线长为6,侧面积为,则下列说法正确的是( )
A. 该圆锥的体积为 B. 该圆锥的内切球的体积为
C. 该圆锥的外接球的表面积为 D. 该圆锥的内接正方体的棱长为
11. 已知的内角所对的边分别为a,b,c,下列四个命题中正确的是( )
A. 若,则一定是钝角三角形
B. 若,则一定是锐角三角形
C. 若,则一定是等腰三角形
D. 若,则一定是等边三角形
12. 已知三棱锥中,分别是的中点,P是棱AC上除端点外的动点,下列选项正确的是( )
A. 直线PF与AB是异面直线
B. 当时,三棱锥体积为
C. 的最小值为
D. 三棱锥外接球的表面积
第II卷(非选择题)
三、填空题(本大题共4小题,共20.0分)
13. 已知则使得的实数___________.
在中,若,,,则角 A 的值是_________.
我国古代数学著作《九章算术》中用“圭田”一词代指等腰三角形田地,若一“圭田”的腰长为4,顶角的余弦值为,则该“圭田”的底边长为________.
将边长为1的正方形纸片绕着它的一条边所在的直线旋转弧度,则纸片扫过的区域形成的几何体的表面积为____________.
14. 中,角A,B,C所对的边分别为a,b,c,且,,
求 a ;
求的值.
15. 如图矩形是水平放置的一个平面四边形OABC的直观图,其中,,
画出平面四边形OABC的平面图并标出边长,并求平面四边形OABC的面积;
若该四边形OABC以OA为旋转轴,旋转一周,求旋转形成的几何体的体积及表面积.
16. 函数的图象两相邻对称轴之间的距离是,若将的图象上每个点先向左平移个单位长度,再向上平移1个单位长度,所得函数为偶函数.
求的解析式;
若对任意,恒成立,求实数m的取值范围;
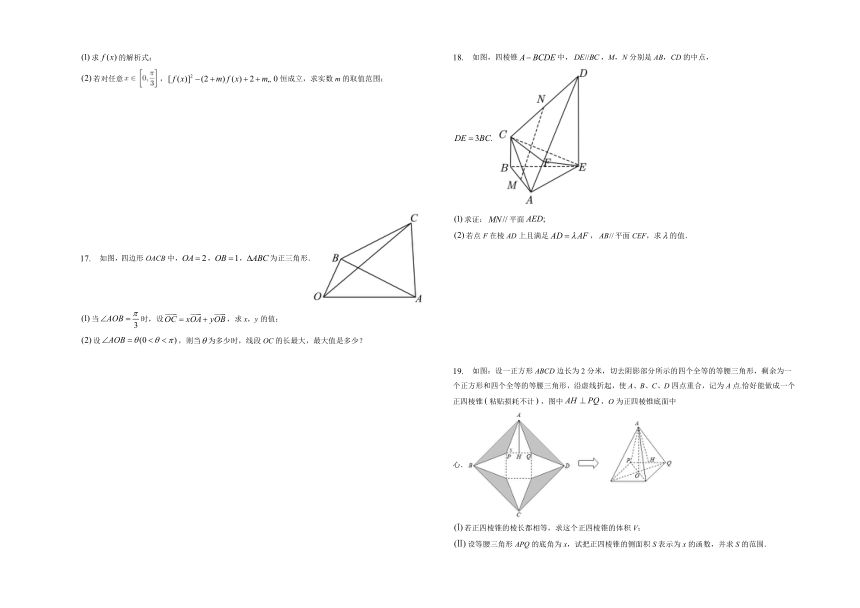
17. 如图,四边形OACB中,,,为正三角形.
当时,设,求x,y的值;
设,则当为多少时,线段OC的长最大,最大值是多少?
18. 如图,四棱锥中,,M,N分别是AB,CD的中点,
求证:平面
若点F在棱AD上且满足,平面CEF,求的值.
19. 如图:设一正方形ABCD边长为2分米,切去阴影部分所示的四个全等的等腰三角形,剩余为一个正方形和四个全等的等腰三角形,沿虚线折起,使A、B、C、D四点重合,记为A点.恰好能做成一个正四棱锥粘贴损耗不计,图中,O为正四棱锥底面中心.
若正四棱锥的棱长都相等,求这个正四棱锥的体积V;
设等腰三角形APQ的底角为x,试把正四棱锥的侧面积S表示为x的函数,并求S的范围.
答案
1.【答案】B
2.【答案】C
3.【答案】A
4.【答案】C
5.【答案】C
6.【答案】C
7.【答案】C
8.【答案】B
9.【答案】BCD
10.【答案】AC
11.【答案】CD
12.【答案】ACD
13.【答案】(1)-2;
(2)或 ;
(3)2;
(4)2+
14.【答案】解:(1)=bcA=-6,A=-,bc=24,
由,解得或(舍去).
=+-2bcA=36+16-26×4×(-)=64,a=8.
(2)由余弦定理,得C===,
C===.
(C-)=C-C=.
15.【答案】解:(1)将直观图还原得 OABC,
.
(2),
,
,
,
所以.
16.【答案】解:由,得,则,
则为偶函数,所以,
又,所以,故;
因为x∈[0,],所以,,
故,,
而恒成立,
即,
整理可得,令,,
设,,
设,且,
则,
由于,,则,所以,
即在区间上单调递增,故,
故,即实数的取值范围是.
17.【答案】解:(1)在 中, , ,
, , ,
解法一:
以 为坐标原点,射线 所在直线为 轴建立平面直角坐标系.
由 ,得 .
由 , ,得
由 及
得 ,
解得 .
解法二:
过点 作 交 于点 ,
在 中 , ,
,
,
(2)由正弦定理得 ,即 ,
所以 ,
所以 ,
,
由余弦定理得
,
因为 ,所以当 时, 取得最大值3.
18.【答案】解:(1)证明:取BE的中点为Q,连接NQ,MQ,
CBDE,N、Q分别为CD、BE的中点;
NQDE,NQ 面AED,DE面AED,
NQ面AED,
又M为BA的中点,
MQAE,MQ 面AED,AE面AEDMQ面AED,
MQNQ=Q,MQ面MNQ,NQ面MNQ ,
面MNQ面AED,又面MNQ,MN面AED.
(2)如图所示:
连接交于点,连接.
∵平面,平面平面,AB 平面ABD,
∴,∴.
在直角梯形中,,∴,
所以,所以,
∴.
19.【答案】解:(I)若正四棱锥的棱长都相等,则在正方形ABCD中,三角形APQ为等边三角形,设边长为a,
∵正方形ABCD边长为2分米,∴AH=a==,解得a==-
∴正四棱锥的棱长a=-
∴PO=a,AO==a,
∴V=×a2×AO=a3=×(-)3=4-
(II)∵AH=PQ×tanx===-PQ
∴PQ=,AH=
∴S=4××PQ×AH
=2×PQ×AH
=2××
= x∈[,)
∵S===≤=2 (当且仅当tanx=1即x=时取等号)
而tanx>0,故s>0
∵S等于2时三角形APQ是等腰直角三角形,顶角PAQ等于90°,阴影部分不存在,折叠后A与O重合,构不成棱锥,∴S的范围为(0,2).
黄州中学(黄冈外校)2022-2023学年高一下学期6月阶段性测试
数学试卷
2023年5月26日 考试范围:第六章-第八章;考试时间:120分钟;联合命题:黄冈袭明卓越教育中心
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
第I卷(选择题)
一、单选题(本大题共8小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1. 在复平面内,复数对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 已知圆台的上下底面圆的半径分别为1与2,高为,则圆台的侧面积为( )
A. B. C. D.
3. 正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( )
A. B. C. D.
4. 已知函数的图象关于点对称,则( )
A. B. C. D.
5. 函数,,则下列结论正确的是( )
A. 是偶函数 B. 是奇函数 C. 是奇函数 D. 是奇函数
6. 如图,已知平面四边形ABCD,,,,AC与BD交于点 O,记,,,则( )
A. B. C. D.
7. 如图所示,在空间四边形ABCD中,E,F分别为AB,AD的中点,分别在,CD上,且则下面几个说法中正确的个数是( )
①E,E,G,H四点共面; ②③若直线EG与直线FH交于点P,则P,A,C三点共线.
A. 0 B. 1 C. 2 D. 3
8. 如图,正方体的棱长为6,P为BC的中点,Q为的中点, 过点,P,Q的平面截正方体所得的截面的面积( )
A. B. C. D.
二、多选题(本大题共4小题,共20.0分。在每小题有多项符合题目要求)
9. 设a,b是两条不重合的直线,,是两个不同的平面.下列四个命题中,正确的是( )
A. 若,,则 B. 若,,则
C. 若,,则 D. 若,,则
10. 已知圆锥的母线长为6,侧面积为,则下列说法正确的是( )
A. 该圆锥的体积为 B. 该圆锥的内切球的体积为
C. 该圆锥的外接球的表面积为 D. 该圆锥的内接正方体的棱长为
11. 已知的内角所对的边分别为a,b,c,下列四个命题中正确的是( )
A. 若,则一定是钝角三角形
B. 若,则一定是锐角三角形
C. 若,则一定是等腰三角形
D. 若,则一定是等边三角形
12. 已知三棱锥中,分别是的中点,P是棱AC上除端点外的动点,下列选项正确的是( )
A. 直线PF与AB是异面直线
B. 当时,三棱锥体积为
C. 的最小值为
D. 三棱锥外接球的表面积
第II卷(非选择题)
三、填空题(本大题共4小题,共20.0分)
13. 已知则使得的实数___________.
在中,若,,,则角 A 的值是_________.
我国古代数学著作《九章算术》中用“圭田”一词代指等腰三角形田地,若一“圭田”的腰长为4,顶角的余弦值为,则该“圭田”的底边长为________.
将边长为1的正方形纸片绕着它的一条边所在的直线旋转弧度,则纸片扫过的区域形成的几何体的表面积为____________.
14. 中,角A,B,C所对的边分别为a,b,c,且,,
求 a ;
求的值.
15. 如图矩形是水平放置的一个平面四边形OABC的直观图,其中,,
画出平面四边形OABC的平面图并标出边长,并求平面四边形OABC的面积;
若该四边形OABC以OA为旋转轴,旋转一周,求旋转形成的几何体的体积及表面积.
16. 函数的图象两相邻对称轴之间的距离是,若将的图象上每个点先向左平移个单位长度,再向上平移1个单位长度,所得函数为偶函数.
求的解析式;
若对任意,恒成立,求实数m的取值范围;
17. 如图,四边形OACB中,,,为正三角形.
当时,设,求x,y的值;
设,则当为多少时,线段OC的长最大,最大值是多少?
18. 如图,四棱锥中,,M,N分别是AB,CD的中点,
求证:平面
若点F在棱AD上且满足,平面CEF,求的值.
19. 如图:设一正方形ABCD边长为2分米,切去阴影部分所示的四个全等的等腰三角形,剩余为一个正方形和四个全等的等腰三角形,沿虚线折起,使A、B、C、D四点重合,记为A点.恰好能做成一个正四棱锥粘贴损耗不计,图中,O为正四棱锥底面中心.
若正四棱锥的棱长都相等,求这个正四棱锥的体积V;
设等腰三角形APQ的底角为x,试把正四棱锥的侧面积S表示为x的函数,并求S的范围.
答案
1.【答案】B
2.【答案】C
3.【答案】A
4.【答案】C
5.【答案】C
6.【答案】C
7.【答案】C
8.【答案】B
9.【答案】BCD
10.【答案】AC
11.【答案】CD
12.【答案】ACD
13.【答案】(1)-2;
(2)或 ;
(3)2;
(4)2+
14.【答案】解:(1)=bcA=-6,A=-,bc=24,
由,解得或(舍去).
=+-2bcA=36+16-26×4×(-)=64,a=8.
(2)由余弦定理,得C===,
C===.
(C-)=C-C=.
15.【答案】解:(1)将直观图还原得 OABC,
.
(2),
,
,
,
所以.
16.【答案】解:由,得,则,
则为偶函数,所以,
又,所以,故;
因为x∈[0,],所以,,
故,,
而恒成立,
即,
整理可得,令,,
设,,
设,且,
则,
由于,,则,所以,
即在区间上单调递增,故,
故,即实数的取值范围是.
17.【答案】解:(1)在 中, , ,
, , ,
解法一:
以 为坐标原点,射线 所在直线为 轴建立平面直角坐标系.
由 ,得 .
由 , ,得
由 及
得 ,
解得 .
解法二:
过点 作 交 于点 ,
在 中 , ,
,
,
(2)由正弦定理得 ,即 ,
所以 ,
所以 ,
,
由余弦定理得
,
因为 ,所以当 时, 取得最大值3.
18.【答案】解:(1)证明:取BE的中点为Q,连接NQ,MQ,
CBDE,N、Q分别为CD、BE的中点;
NQDE,NQ 面AED,DE面AED,
NQ面AED,
又M为BA的中点,
MQAE,MQ 面AED,AE面AEDMQ面AED,
MQNQ=Q,MQ面MNQ,NQ面MNQ ,
面MNQ面AED,又面MNQ,MN面AED.
(2)如图所示:
连接交于点,连接.
∵平面,平面平面,AB 平面ABD,
∴,∴.
在直角梯形中,,∴,
所以,所以,
∴.
19.【答案】解:(I)若正四棱锥的棱长都相等,则在正方形ABCD中,三角形APQ为等边三角形,设边长为a,
∵正方形ABCD边长为2分米,∴AH=a==,解得a==-
∴正四棱锥的棱长a=-
∴PO=a,AO==a,
∴V=×a2×AO=a3=×(-)3=4-
(II)∵AH=PQ×tanx===-PQ
∴PQ=,AH=
∴S=4××PQ×AH
=2×PQ×AH
=2××
= x∈[,)
∵S===≤=2 (当且仅当tanx=1即x=时取等号)
而tanx>0,故s>0
∵S等于2时三角形APQ是等腰直角三角形,顶角PAQ等于90°,阴影部分不存在,折叠后A与O重合,构不成棱锥,∴S的范围为(0,2).
同课章节目录
