2023——2024学年苏科版数学八年级上册1.1全等图形 自主学习同步练习题(含解析)
文档属性
| 名称 | 2023——2024学年苏科版数学八年级上册1.1全等图形 自主学习同步练习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 230.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-10 00:00:00 | ||
图片预览

文档简介
2023-2024学年苏科版八年级数学上册《1.1全等图形》自主学习同步练习题(附答案)
一、单选题
1.全等图形是指两个图形( )
A.大小相同 B.形状相同
C.能够完全重合 D.相等
2.下列图形中,和所给图形全等的图形是( )
A. B. C. D.
3.如图,与所给图案是全等图形的是( )
A. B. C. D.
4.下列图形中被虚线分成的两部分不是全等形的是( )
A.等腰梯形 B.正方形
C.正六边形 D.正五角星
5.观察如下图所示的各个图形,其中全等图形正确的是( ).
A.②≌④ B.⑤≌⑧ C.①≌⑥ D.③≌⑦
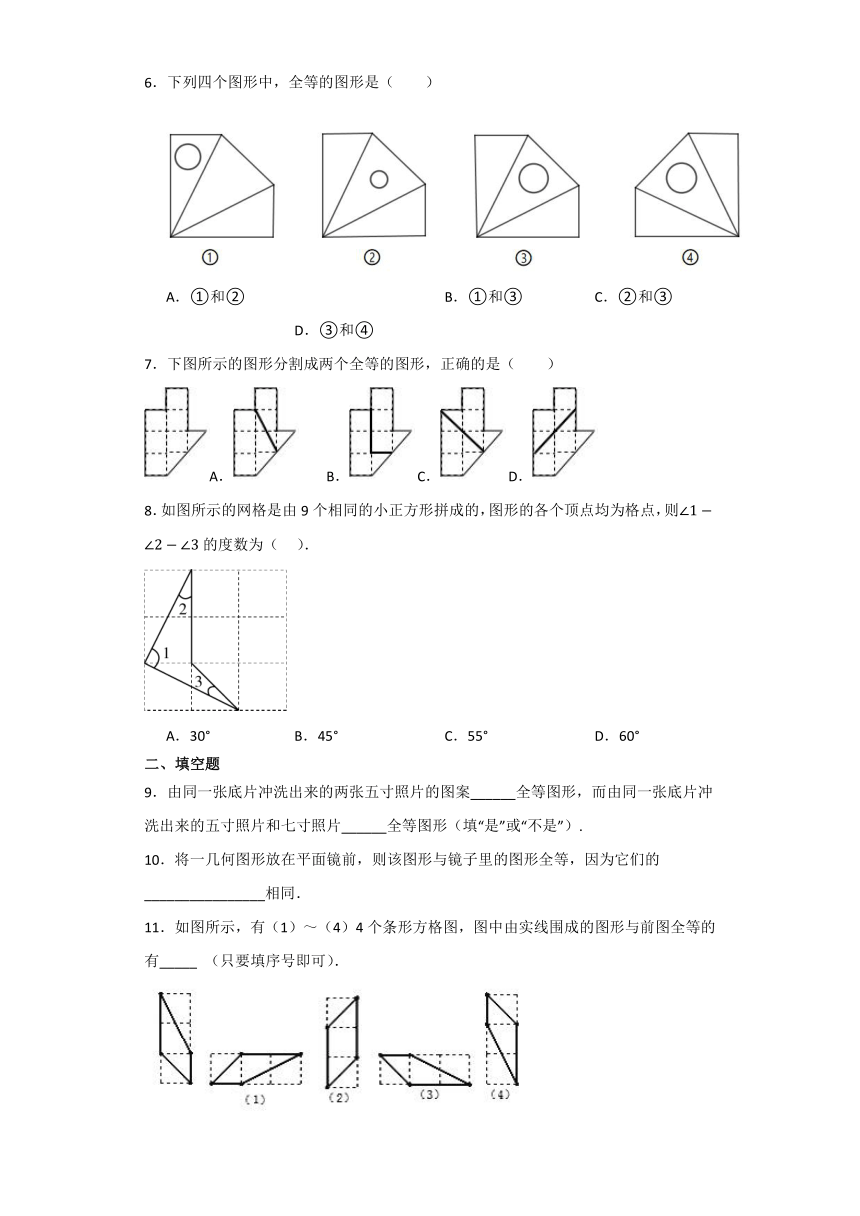
6.下列四个图形中,全等的图形是( )
A.①和② B.①和③ C.②和③ D.③和④
7.下图所示的图形分割成两个全等的图形,正确的是( )
A. B. C. D.
8.如图所示的网格是由9个相同的小正方形拼成的,图形的各个顶点均为格点,则的度数为( ).
A.30° B.45° C.55° D.60°
二、填空题
9.由同一张底片冲洗出来的两张五寸照片的图案______全等图形,而由同一张底片冲洗出来的五寸照片和七寸照片______全等图形(填“是”或“不是”).
10.将一几何图形放在平面镜前,则该图形与镜子里的图形全等,因为它们的________________相同.
11.如图所示,有(1)~(4)4个条形方格图,图中由实线围成的图形与前图全等的有_____ (只要填序号即可).
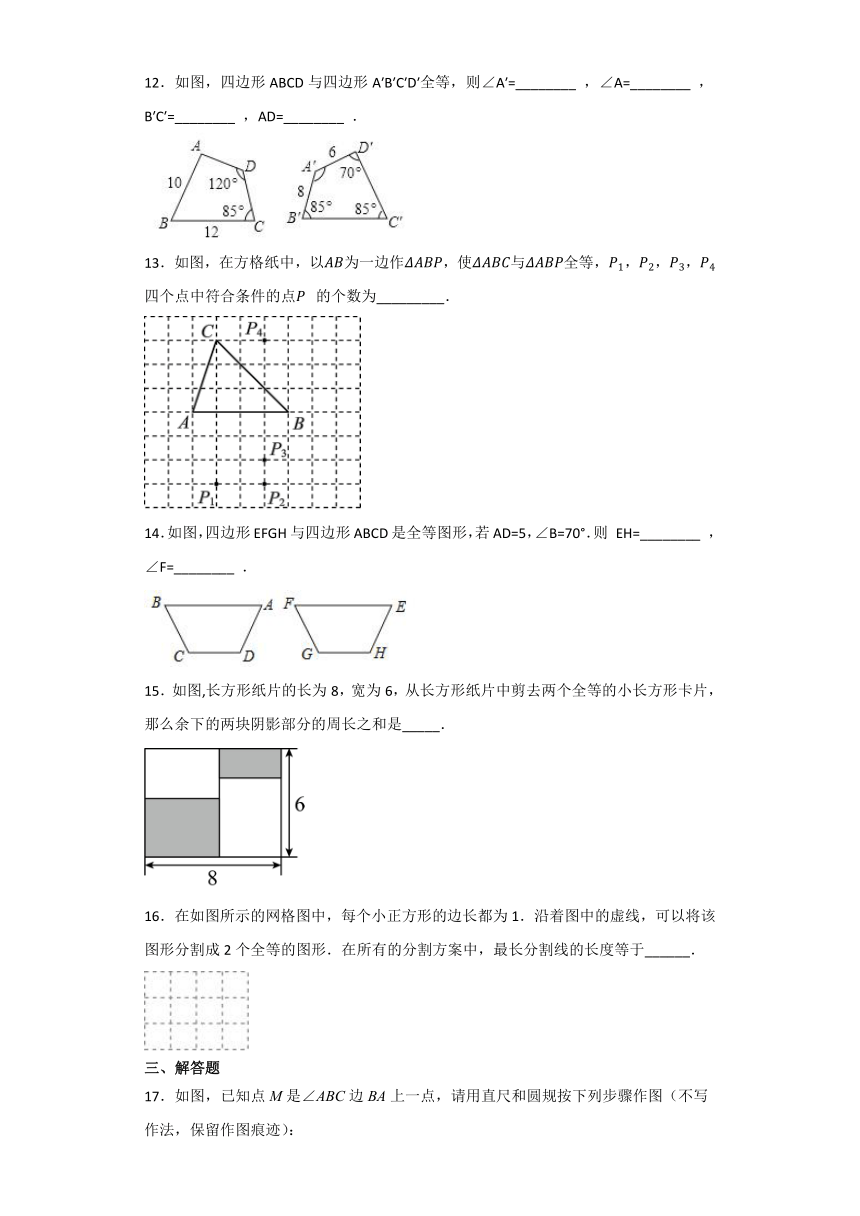
12.如图,四边形ABCD与四边形A′B′C′D′全等,则∠A′=________ ,∠A=________ ,B′C′=________ ,AD=________ .
13.如图,在方格纸中,以为一边作,使与全等,,,,四个点中符合条件的点的个数为_________.
14.如图,四边形EFGH与四边形ABCD是全等图形,若AD=5,∠B=70°.则 EH=________ ,∠F=________ .
15.如图,长方形纸片的长为8,宽为6,从长方形纸片中剪去两个全等的小长方形卡片,那么余下的两块阴影部分的周长之和是_____.
16.在如图所示的网格图中,每个小正方形的边长都为1.沿着图中的虚线,可以将该图形分割成2个全等的图形.在所有的分割方案中,最长分割线的长度等于______.
三、解答题
17.如图,已知点M是∠ABC边BA上一点,请用直尺和圆规按下列步骤作图(不写作法,保留作图痕迹):
(1)在射线BC上作线段BO,使BO=BM;
(2)以点O为顶点,OB为一边作∠BON,使∠BON=∠B,边ON交射线BA于点N;
18.用三种方法将如图所示的等边三角形分成三个全等的图形.
19.下图是几个4×4的正方形方格图,请沿着格线画出四种不同的分法,把它分成两个全等图形.
20.如图,用三种不同的方法沿网格线把正方形分割成4个全等的图形(三种方法得到的图形相互间不全等).
参考答案:
1.解:全等图形是指两个图形的形状和大小都相等,能够完全重合,
故选C.
2.解:根据全等图形的定义只需找出与原图形大小相等,形状相同的图形即可,A、B、C选项均不符合题意,只有D符合题意,D中的图形相对于原图形顺时针作了180°的旋转变换.
故选D.
3.解:由全等图形的定义可知,与所给图案是全等图形的是选项C,
故选:C.
4.解:观察选项可知,选项B,C,D中的虚线把图形分成两个完全重合的两部分,而选项A的虚线把图形分成两个不能重合的三角形,故选项A这两部分不是全等图形;
故选:A.
5.解:观察可知 ②≌⑤,③≌⑧,①≌⑥,
故选C.
6.解:③和④可以完全重合,因此全等的图形是③和④.
故选D.
点评:此题主要考查了全等图形,关键是掌握全等图形的概念.
7.解:图形分割成两个全等的图形,如图所示:
故选B.
8.解:如图,则,,,
∴ ,
故选:B.
9. 解:由同一张底片冲洗出来的两张五寸照片的图案是全等图形,而由同一张底片冲洗出来的五寸照片和七寸照片不是全等图形.
故答案为:是,不是.
10.解:∵平面镜不改变图形的大小与形状,
∴答案为大小和形状,
故答案为:大小和形状.
11.解:观察图形,可得(1)(3)(4)各图形的角度与原图形相等,边长与原图形相等,由此可得与前图全等的有(1)、(3)、(4).
12.解:∵四边形ABCD与四边形A′B′C′D′全等,
由题意得:∠A′=∠D =∠120°,∠D′=∠A=70°,B′C′=CB=12,AD = D′A′=6.
13.解:要使△ABP与△ABC全等,点P到AB的距离应该等于点C到AB的距离,即3个单位长度,故点P的位置可以是三个,故答案为3.
14.解:∵四边形EFGH与四边形ABCD是全等图形,AD=5,∠B=70°,
∴EH=AD=5,∠F=∠B=70°,
故答案为5,70°.
15.解:设两个全等的小长方形卡片的长为a,宽为b,
则左边的阴影长方形的周长=2(a+6-b)=12+2a-2b,
右边的阴影长方形的周长=2(b+6-a)=12+2b-2a,
∴两块阴影部分的周长之和=(12+2a-2b)+( 12+2b-2a)=24.
故答案为:24.
16.解:分割方案如图所示:
由图可得,最长分割线的长度等于7.
故答案为:7.
17.(1)解:如下图,线段BO即为所求;
(2)如上图,射线ON即为所求.
18.解:如图所示(答案不唯一).
19.解:
20.解:如图所示:
一、单选题
1.全等图形是指两个图形( )
A.大小相同 B.形状相同
C.能够完全重合 D.相等
2.下列图形中,和所给图形全等的图形是( )
A. B. C. D.
3.如图,与所给图案是全等图形的是( )
A. B. C. D.
4.下列图形中被虚线分成的两部分不是全等形的是( )
A.等腰梯形 B.正方形
C.正六边形 D.正五角星
5.观察如下图所示的各个图形,其中全等图形正确的是( ).
A.②≌④ B.⑤≌⑧ C.①≌⑥ D.③≌⑦
6.下列四个图形中,全等的图形是( )
A.①和② B.①和③ C.②和③ D.③和④
7.下图所示的图形分割成两个全等的图形,正确的是( )
A. B. C. D.
8.如图所示的网格是由9个相同的小正方形拼成的,图形的各个顶点均为格点,则的度数为( ).
A.30° B.45° C.55° D.60°
二、填空题
9.由同一张底片冲洗出来的两张五寸照片的图案______全等图形,而由同一张底片冲洗出来的五寸照片和七寸照片______全等图形(填“是”或“不是”).
10.将一几何图形放在平面镜前,则该图形与镜子里的图形全等,因为它们的________________相同.
11.如图所示,有(1)~(4)4个条形方格图,图中由实线围成的图形与前图全等的有_____ (只要填序号即可).
12.如图,四边形ABCD与四边形A′B′C′D′全等,则∠A′=________ ,∠A=________ ,B′C′=________ ,AD=________ .
13.如图,在方格纸中,以为一边作,使与全等,,,,四个点中符合条件的点的个数为_________.
14.如图,四边形EFGH与四边形ABCD是全等图形,若AD=5,∠B=70°.则 EH=________ ,∠F=________ .
15.如图,长方形纸片的长为8,宽为6,从长方形纸片中剪去两个全等的小长方形卡片,那么余下的两块阴影部分的周长之和是_____.
16.在如图所示的网格图中,每个小正方形的边长都为1.沿着图中的虚线,可以将该图形分割成2个全等的图形.在所有的分割方案中,最长分割线的长度等于______.
三、解答题
17.如图,已知点M是∠ABC边BA上一点,请用直尺和圆规按下列步骤作图(不写作法,保留作图痕迹):
(1)在射线BC上作线段BO,使BO=BM;
(2)以点O为顶点,OB为一边作∠BON,使∠BON=∠B,边ON交射线BA于点N;
18.用三种方法将如图所示的等边三角形分成三个全等的图形.
19.下图是几个4×4的正方形方格图,请沿着格线画出四种不同的分法,把它分成两个全等图形.
20.如图,用三种不同的方法沿网格线把正方形分割成4个全等的图形(三种方法得到的图形相互间不全等).
参考答案:
1.解:全等图形是指两个图形的形状和大小都相等,能够完全重合,
故选C.
2.解:根据全等图形的定义只需找出与原图形大小相等,形状相同的图形即可,A、B、C选项均不符合题意,只有D符合题意,D中的图形相对于原图形顺时针作了180°的旋转变换.
故选D.
3.解:由全等图形的定义可知,与所给图案是全等图形的是选项C,
故选:C.
4.解:观察选项可知,选项B,C,D中的虚线把图形分成两个完全重合的两部分,而选项A的虚线把图形分成两个不能重合的三角形,故选项A这两部分不是全等图形;
故选:A.
5.解:观察可知 ②≌⑤,③≌⑧,①≌⑥,
故选C.
6.解:③和④可以完全重合,因此全等的图形是③和④.
故选D.
点评:此题主要考查了全等图形,关键是掌握全等图形的概念.
7.解:图形分割成两个全等的图形,如图所示:
故选B.
8.解:如图,则,,,
∴ ,
故选:B.
9. 解:由同一张底片冲洗出来的两张五寸照片的图案是全等图形,而由同一张底片冲洗出来的五寸照片和七寸照片不是全等图形.
故答案为:是,不是.
10.解:∵平面镜不改变图形的大小与形状,
∴答案为大小和形状,
故答案为:大小和形状.
11.解:观察图形,可得(1)(3)(4)各图形的角度与原图形相等,边长与原图形相等,由此可得与前图全等的有(1)、(3)、(4).
12.解:∵四边形ABCD与四边形A′B′C′D′全等,
由题意得:∠A′=∠D =∠120°,∠D′=∠A=70°,B′C′=CB=12,AD = D′A′=6.
13.解:要使△ABP与△ABC全等,点P到AB的距离应该等于点C到AB的距离,即3个单位长度,故点P的位置可以是三个,故答案为3.
14.解:∵四边形EFGH与四边形ABCD是全等图形,AD=5,∠B=70°,
∴EH=AD=5,∠F=∠B=70°,
故答案为5,70°.
15.解:设两个全等的小长方形卡片的长为a,宽为b,
则左边的阴影长方形的周长=2(a+6-b)=12+2a-2b,
右边的阴影长方形的周长=2(b+6-a)=12+2b-2a,
∴两块阴影部分的周长之和=(12+2a-2b)+( 12+2b-2a)=24.
故答案为:24.
16.解:分割方案如图所示:
由图可得,最长分割线的长度等于7.
故答案为:7.
17.(1)解:如下图,线段BO即为所求;
(2)如上图,射线ON即为所求.
18.解:如图所示(答案不唯一).
19.解:
20.解:如图所示:
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
