2023—2024学年人教版数学八年级上册11.3多边形及其内角和自主学习同步练习题(含答案)
文档属性
| 名称 | 2023—2024学年人教版数学八年级上册11.3多边形及其内角和自主学习同步练习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 792.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-10 10:21:43 | ||
图片预览



文档简介
2023-2024学年人教版八年级数学上册《11.3多边形及其内角和》
自主学习同步练习题(附答案)
一、单选题
1.若一个多边形的内角和是,则该多边形的边数为( )
A.4 B.5 C.6 D.7
2.已知正多边形的一个外角等于,则该正多边形的边数为( )
A.十 B.九 C.八 D.七
3.十边形的内角和为( )
A.1800° B.1620° C.1440° D.1260°
4.如图,一束太阳光线平行照射在放置于地面的正六边形上,若,则的度数为( )
A. B. C. D.
5.当多边形的边数增加1时,它的内角和与外角和的变化情况是( )
A.都不变 B.都增加
C.内角和增加,外角和减少 D.内角和增加,外角和不变
6.题目:“如图,用10个全等的正五边形依次排列可以围成环状.若改为正n边形也能围成环状,除了外,请求出其他所有n的可能的值.”对于其答案,甲答:,乙答:,则正确的是( )
A.只有甲答的对 B.只有乙答的对
C.甲、乙答案合在一起才完整 D.甲、乙答案合在一起也不完整
7.等边三角形、正方形及正五边形各一个,按下图放在同一平面内,则( )
A. B. C. D.
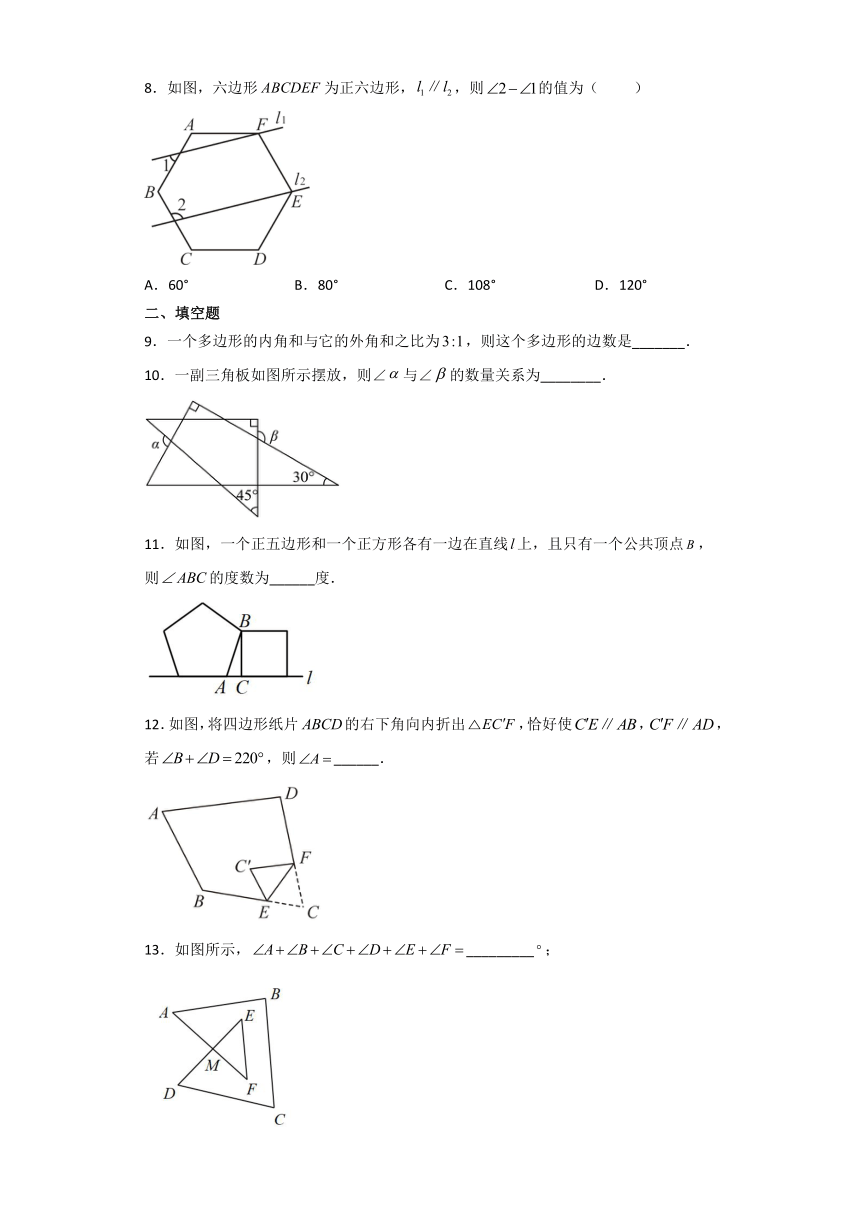
8.如图,六边形为正六边形,,则的值为( )
A.60° B.80° C.108° D.120°
二、填空题
9.一个多边形的内角和与它的外角和之比为,则这个多边形的边数是_______.
10.一副三角板如图所示摆放,则∠与∠的数量关系为________.
11.如图,一个正五边形和一个正方形各有一边在直线上,且只有一个公共顶点,则的度数为______度.
12.如图,将四边形纸片的右下角向内折出,恰好使,,若,则______.
13.如图所示,_________;
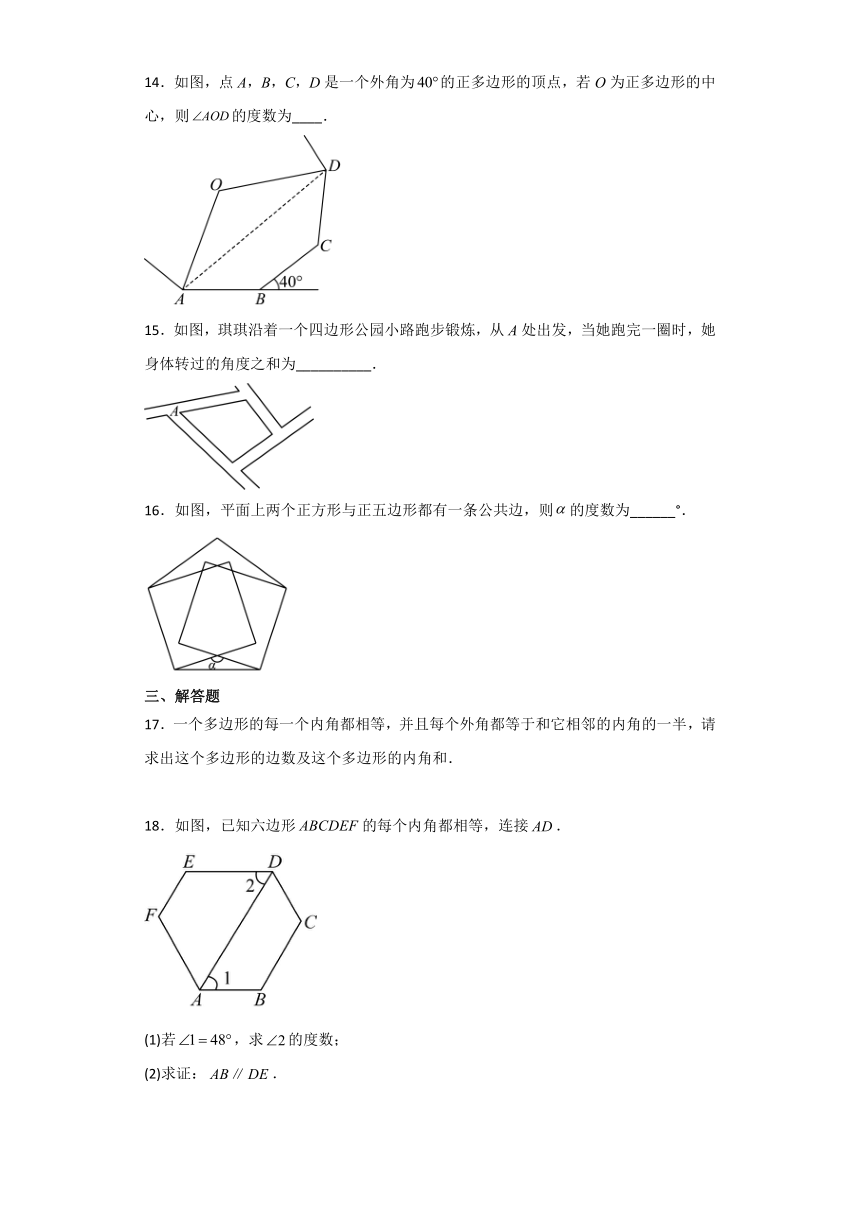
14.如图,点A,B,C,D是一个外角为的正多边形的顶点,若O为正多边形的中心,则的度数为____.
15.如图,琪琪沿着一个四边形公园小路跑步锻炼,从A处出发,当她跑完一圈时,她身体转过的角度之和为__________.
16.如图,平面上两个正方形与正五边形都有一条公共边,则的度数为______°.
三、解答题
17.一个多边形的每一个内角都相等,并且每个外角都等于和它相邻的内角的一半,请求出这个多边形的边数及这个多边形的内角和.
18.如图,已知六边形的每个内角都相等,连接.
(1)若,求的度数;
(2)求证:.
19.如图,在四边形ABCD中,∠A与∠C互补,∠ABC、∠ADC的平分线分别交CD、AB于点E、F,EG∥AB.
(1)∠1与∠2有怎样的数量关系 为什么
(2)若∠A=100°,∠1=42°,求∠CEG的度数.
20.(1)已知:如图1,P为△ADC内一点,DP、CP分别平分∠ADC和∠ACD.如果∠A=50°,那么∠P=_____°;如果∠A=100°,那么∠P=______°.(直接写出答案,不必说明理由)
(2)如图2,P为四边形ABCD内一点DP,CP分别平分∠ADC和∠BCD,请直接写出∠P与∠A+∠B的数量关系:______(直接写出答案,不必说明理由)
(3)如图3,P为五边形ABCDEP内一点;DP、CP分别平分∠EDC、∠BCD,试探究∠P与∠A+∠B+∠E的数量关系,并说明理由.
21.如图①,已知线段AB,CD相交于点O,连接AC,BD,我们把形如图①的图形称之为“8字形”.如图②,∠CAB和∠BDC的平分线AP和DP相交于点P,并且与CD,AB分别相交于M,N.试解答下列问题:
(1)在图①中,写出一个关于∠A、∠B、∠C、∠D的关系的等式 .
(2)在图②中,若∠B=96°,∠C=100°,求∠P的度数;
(3)在图②中,若设∠C=α,∠B=β,∠CAP=∠CAB,∠CDP=∠CDB,试问∠P与∠C,∠B之间存在着怎样的数量关系(用α,β表示∠P),并说明理由;
(4)如图③,则∠A+∠B+∠C+∠D+∠E+∠F的度数为 .
参考答案:
1.解:设多边形的边数是,则
,
解得.
故选:B.
2.解:边数,所以边数为九 故选B.
3.解:根据多边形内角和公式,当时,
十边形的内角和为,故选:C.
4.解:如图:
∵正六边形的一个外角的度数为:,
∴正六边形的一个内角的度数为:,
即:,
∵一束太阳光线平行照射在放置于地面的正六边形上,,
∴,
∴,
∴;故选B.
5.解:当多边形边数增加1时,内角和增加,外角和是个固定值为.
故选:D.
6.解:如图所示,
∵正n边形也能围成环状,
∴,
∴,
∴由题意可得,圆环里面是以为边的正多边形,
∴这个正多边形的外角为,
∴这个正多边形的边数为,
∴是正整数,
∴当时,,符合题意;
当时,,符合题意;
当时,,符合题意;
当时,,符合题意.
综上所述,其他所有n的可能的值为6,8,12.
故选:D.
7.解:正三角形的每个内角为,
正五边形的每个内角,
正方形的每一个内角为,
∴,
故选:A.
8.解:如图,延长交于点G,
∵六边形为正六边形,
∴,
∵,
∴,
∵,
∴.
故选:A.
9.解:设多边形的边数是n,则
,
整理得,
解得.
故答案为:8.
10.解:在四边形中,,
,,
,
,,
,
故答案为:.
11.解:因为正五边形的每一个外角的度数为,
∴.
∵同理可得:,
在中,
∴.
故答案为:.
12.解:∵,,
∴,,
∵,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
故答案为:.
13.解:如图,连接;
∵
∴
∵
∴
故答案为:.
14.解:连接、,
正多边形的每个外角相等,且其和为,
据此可得多边形的边数为:,
,
.
故答案为:
15.解:多边形的外角和等于360度,
琪琪跑完一圈时,身体转过的角度之和是360度.
故答案为:360度.
16.解:由题意可得:
正五边形的每个内角为:,正方形的内角为,
即:,,
则,
同理可得:,
∴,即:的度数为,
故答案为:144.
17.解:∵多边形的每一个内角都相等,
∴设多边形的每一个内角为,则每一个外角为,由题意得,,解方程得,,即多边形的内角为,则多边形的一个外角为,
∴由多边形的外角和等于可得,多边形的边数为:,
∴多边形的内角和为,
故答案为:六边形,内角和为.
18.解:(1)∵六边形的每个内角都相等,
∴一个内角为,
∴,
∵,
∴,
∵,
∴
(2)∵,,
∴,
∴.
19.解:(1)∠1与∠2互余.
∵四边形ABCD的内角和为360°,∠A与∠C互补,
∴∠ABC+∠ADC=360°-180°=180°,
∵BE、DF分别平分∠ABC、∠ADC,
∴∠1=∠ADC,∠ABE=∠ABC,
∵EG∥AB,
∴∠2=∠ABE,
∴∠1+∠2=∠ADC+∠ABC=90°,
即∠1与∠2互余.
(2)∵∠A=100°,∠1=42°,
∴∠C=80°,∠2=48°,
∴∠ABE=∠CBE=48°,
∴∠BEC=180°-48°-80°=52°,
∴∠CEG=52°-48°=4°.
20.解:(1)∵∠A=50°,
∴∠ADC+∠ACD=130°,
∵DP、CP分别平分∠ADC和∠ACD,
∴,
∴,
∴;
同理:如果∠A=100°,那么∠P=140°;
故答案为:115,140;
(2)∵DP、CP分别平分∠ADC和∠BCD,
∴,
∴
;
∴;
故答案为:;
(3)五边形ABCDE的内角和为:,
∵DP、CP分别平分∠EDC、∠BCD,
∴,
∴
,
即;
21.(1)解:结论:∠A+∠C=∠B+∠D.
理由:如图中,
∠A+∠C+∠AOC =∠B+∠D+∠DOB=180°,
∵∠AOC=∠DOB,
∴∠A+∠C=∠B+∠D.
故答案为:∠A+∠C=∠B+∠D;
(2)解:∵∠CAB和∠BDC的平分线AP和DP相交于点P,
∴∠CAP=∠BAP,∠BDP=∠CDP,
∵∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,
∴∠C-∠P=∠P-∠B,
即∠P=(∠C+∠B),
∵∠C=100°,∠B=96°,
∴∠P=(100°+96°)=98°;
(3)解:结论:∠P=(β+2α).
理由:∵∠CAP=∠CAB,∠CDP=∠CDB,
∴∠BAP=∠BAC,∠BDP=∠BDC,
∵∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,
∴∠C-∠P=∠BDC-∠BAC,∠P-∠B=∠BDC-∠BAC,
∴2(∠C-∠P)=∠P-∠B,
∴∠P=(∠B+2∠C),
∵∠C=α,∠B=β,
∴∠P=(β+2α);
(4)
解:∵∠B+∠A=∠1,∠C+∠D=∠2,
∴∠A+∠B+∠C+∠D=∠1+∠2,
∵∠1+∠2+∠F+∠E=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
故答案为:360°.
自主学习同步练习题(附答案)
一、单选题
1.若一个多边形的内角和是,则该多边形的边数为( )
A.4 B.5 C.6 D.7
2.已知正多边形的一个外角等于,则该正多边形的边数为( )
A.十 B.九 C.八 D.七
3.十边形的内角和为( )
A.1800° B.1620° C.1440° D.1260°
4.如图,一束太阳光线平行照射在放置于地面的正六边形上,若,则的度数为( )
A. B. C. D.
5.当多边形的边数增加1时,它的内角和与外角和的变化情况是( )
A.都不变 B.都增加
C.内角和增加,外角和减少 D.内角和增加,外角和不变
6.题目:“如图,用10个全等的正五边形依次排列可以围成环状.若改为正n边形也能围成环状,除了外,请求出其他所有n的可能的值.”对于其答案,甲答:,乙答:,则正确的是( )
A.只有甲答的对 B.只有乙答的对
C.甲、乙答案合在一起才完整 D.甲、乙答案合在一起也不完整
7.等边三角形、正方形及正五边形各一个,按下图放在同一平面内,则( )
A. B. C. D.
8.如图,六边形为正六边形,,则的值为( )
A.60° B.80° C.108° D.120°
二、填空题
9.一个多边形的内角和与它的外角和之比为,则这个多边形的边数是_______.
10.一副三角板如图所示摆放,则∠与∠的数量关系为________.
11.如图,一个正五边形和一个正方形各有一边在直线上,且只有一个公共顶点,则的度数为______度.
12.如图,将四边形纸片的右下角向内折出,恰好使,,若,则______.
13.如图所示,_________;
14.如图,点A,B,C,D是一个外角为的正多边形的顶点,若O为正多边形的中心,则的度数为____.
15.如图,琪琪沿着一个四边形公园小路跑步锻炼,从A处出发,当她跑完一圈时,她身体转过的角度之和为__________.
16.如图,平面上两个正方形与正五边形都有一条公共边,则的度数为______°.
三、解答题
17.一个多边形的每一个内角都相等,并且每个外角都等于和它相邻的内角的一半,请求出这个多边形的边数及这个多边形的内角和.
18.如图,已知六边形的每个内角都相等,连接.
(1)若,求的度数;
(2)求证:.
19.如图,在四边形ABCD中,∠A与∠C互补,∠ABC、∠ADC的平分线分别交CD、AB于点E、F,EG∥AB.
(1)∠1与∠2有怎样的数量关系 为什么
(2)若∠A=100°,∠1=42°,求∠CEG的度数.
20.(1)已知:如图1,P为△ADC内一点,DP、CP分别平分∠ADC和∠ACD.如果∠A=50°,那么∠P=_____°;如果∠A=100°,那么∠P=______°.(直接写出答案,不必说明理由)
(2)如图2,P为四边形ABCD内一点DP,CP分别平分∠ADC和∠BCD,请直接写出∠P与∠A+∠B的数量关系:______(直接写出答案,不必说明理由)
(3)如图3,P为五边形ABCDEP内一点;DP、CP分别平分∠EDC、∠BCD,试探究∠P与∠A+∠B+∠E的数量关系,并说明理由.
21.如图①,已知线段AB,CD相交于点O,连接AC,BD,我们把形如图①的图形称之为“8字形”.如图②,∠CAB和∠BDC的平分线AP和DP相交于点P,并且与CD,AB分别相交于M,N.试解答下列问题:
(1)在图①中,写出一个关于∠A、∠B、∠C、∠D的关系的等式 .
(2)在图②中,若∠B=96°,∠C=100°,求∠P的度数;
(3)在图②中,若设∠C=α,∠B=β,∠CAP=∠CAB,∠CDP=∠CDB,试问∠P与∠C,∠B之间存在着怎样的数量关系(用α,β表示∠P),并说明理由;
(4)如图③,则∠A+∠B+∠C+∠D+∠E+∠F的度数为 .
参考答案:
1.解:设多边形的边数是,则
,
解得.
故选:B.
2.解:边数,所以边数为九 故选B.
3.解:根据多边形内角和公式,当时,
十边形的内角和为,故选:C.
4.解:如图:
∵正六边形的一个外角的度数为:,
∴正六边形的一个内角的度数为:,
即:,
∵一束太阳光线平行照射在放置于地面的正六边形上,,
∴,
∴,
∴;故选B.
5.解:当多边形边数增加1时,内角和增加,外角和是个固定值为.
故选:D.
6.解:如图所示,
∵正n边形也能围成环状,
∴,
∴,
∴由题意可得,圆环里面是以为边的正多边形,
∴这个正多边形的外角为,
∴这个正多边形的边数为,
∴是正整数,
∴当时,,符合题意;
当时,,符合题意;
当时,,符合题意;
当时,,符合题意.
综上所述,其他所有n的可能的值为6,8,12.
故选:D.
7.解:正三角形的每个内角为,
正五边形的每个内角,
正方形的每一个内角为,
∴,
故选:A.
8.解:如图,延长交于点G,
∵六边形为正六边形,
∴,
∵,
∴,
∵,
∴.
故选:A.
9.解:设多边形的边数是n,则
,
整理得,
解得.
故答案为:8.
10.解:在四边形中,,
,,
,
,,
,
故答案为:.
11.解:因为正五边形的每一个外角的度数为,
∴.
∵同理可得:,
在中,
∴.
故答案为:.
12.解:∵,,
∴,,
∵,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
故答案为:.
13.解:如图,连接;
∵
∴
∵
∴
故答案为:.
14.解:连接、,
正多边形的每个外角相等,且其和为,
据此可得多边形的边数为:,
,
.
故答案为:
15.解:多边形的外角和等于360度,
琪琪跑完一圈时,身体转过的角度之和是360度.
故答案为:360度.
16.解:由题意可得:
正五边形的每个内角为:,正方形的内角为,
即:,,
则,
同理可得:,
∴,即:的度数为,
故答案为:144.
17.解:∵多边形的每一个内角都相等,
∴设多边形的每一个内角为,则每一个外角为,由题意得,,解方程得,,即多边形的内角为,则多边形的一个外角为,
∴由多边形的外角和等于可得,多边形的边数为:,
∴多边形的内角和为,
故答案为:六边形,内角和为.
18.解:(1)∵六边形的每个内角都相等,
∴一个内角为,
∴,
∵,
∴,
∵,
∴
(2)∵,,
∴,
∴.
19.解:(1)∠1与∠2互余.
∵四边形ABCD的内角和为360°,∠A与∠C互补,
∴∠ABC+∠ADC=360°-180°=180°,
∵BE、DF分别平分∠ABC、∠ADC,
∴∠1=∠ADC,∠ABE=∠ABC,
∵EG∥AB,
∴∠2=∠ABE,
∴∠1+∠2=∠ADC+∠ABC=90°,
即∠1与∠2互余.
(2)∵∠A=100°,∠1=42°,
∴∠C=80°,∠2=48°,
∴∠ABE=∠CBE=48°,
∴∠BEC=180°-48°-80°=52°,
∴∠CEG=52°-48°=4°.
20.解:(1)∵∠A=50°,
∴∠ADC+∠ACD=130°,
∵DP、CP分别平分∠ADC和∠ACD,
∴,
∴,
∴;
同理:如果∠A=100°,那么∠P=140°;
故答案为:115,140;
(2)∵DP、CP分别平分∠ADC和∠BCD,
∴,
∴
;
∴;
故答案为:;
(3)五边形ABCDE的内角和为:,
∵DP、CP分别平分∠EDC、∠BCD,
∴,
∴
,
即;
21.(1)解:结论:∠A+∠C=∠B+∠D.
理由:如图中,
∠A+∠C+∠AOC =∠B+∠D+∠DOB=180°,
∵∠AOC=∠DOB,
∴∠A+∠C=∠B+∠D.
故答案为:∠A+∠C=∠B+∠D;
(2)解:∵∠CAB和∠BDC的平分线AP和DP相交于点P,
∴∠CAP=∠BAP,∠BDP=∠CDP,
∵∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,
∴∠C-∠P=∠P-∠B,
即∠P=(∠C+∠B),
∵∠C=100°,∠B=96°,
∴∠P=(100°+96°)=98°;
(3)解:结论:∠P=(β+2α).
理由:∵∠CAP=∠CAB,∠CDP=∠CDB,
∴∠BAP=∠BAC,∠BDP=∠BDC,
∵∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,
∴∠C-∠P=∠BDC-∠BAC,∠P-∠B=∠BDC-∠BAC,
∴2(∠C-∠P)=∠P-∠B,
∴∠P=(∠B+2∠C),
∵∠C=α,∠B=β,
∴∠P=(β+2α);
(4)
解:∵∠B+∠A=∠1,∠C+∠D=∠2,
∴∠A+∠B+∠C+∠D=∠1+∠2,
∵∠1+∠2+∠F+∠E=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
故答案为:360°.
