4.2.2指数函数的图象和性质(第1课时) 课件(共36张PPT)
文档属性
| 名称 | 4.2.2指数函数的图象和性质(第1课时) 课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 58.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-09 16:26:38 | ||
图片预览


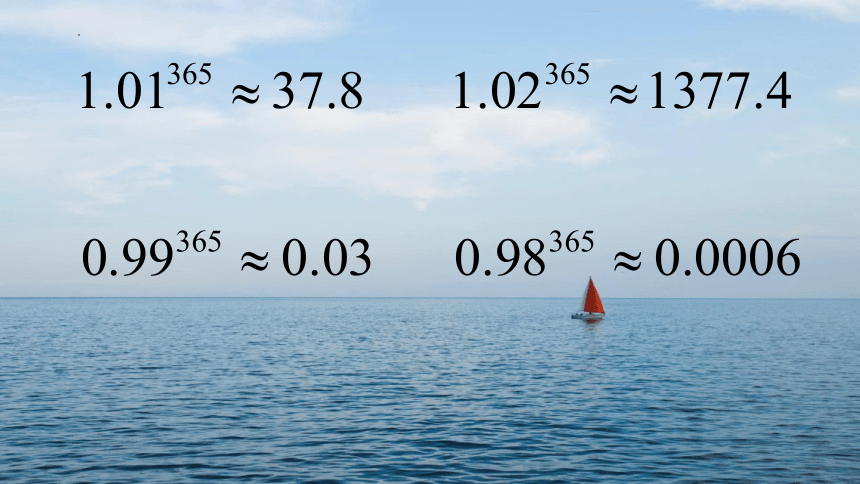







文档简介
(共36张PPT)
4.2.2指数函数的图象与性质(1)
第四章 指数函数与对数函数
人教A版 必修一
课堂展示
第一部分
4.2.2指数函数的图象与性质(1)
第四章 指数函数与对数函数
人教A版 必修一
学习目标 1.掌握指数函数的图象以及函数图象随参数变化而变化的规律;
2.能从具体的指数函数图象,推广到一般指数函数的图象规律
进而得到指数函数的性质,体会特殊到一般、数形结合、分类
讨论的数学思想;.
3. 提升数学抽象、逻辑推理、数学运算、数据分析等数学学科
素养。
学习重点 指数函数的图象及其随参数变化而变化的规律
学习难点 对底数的分类,如何由图象、解析式归纳指数函数的性质
学习目标、重难点
课前小测
C
[1,+∞)
指数函数
一般地,函数 叫做指数函数。
其中指数x是自变量,定义域是R。
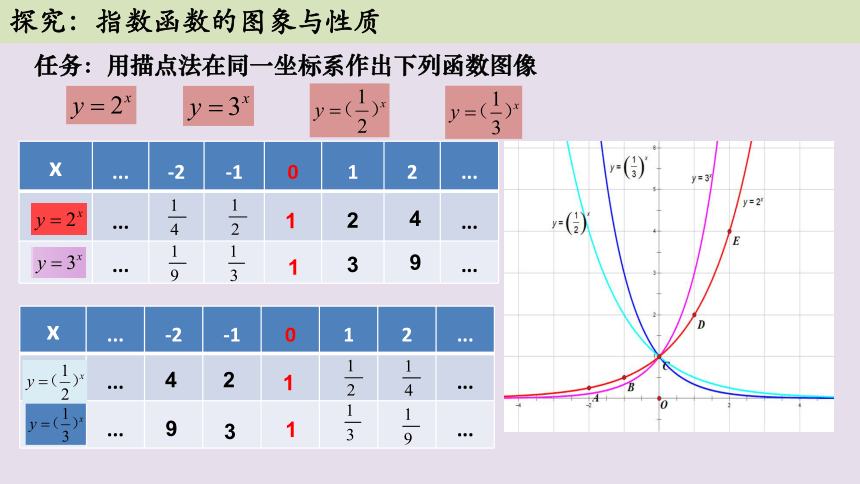
任务:用描点法在同一坐标系作出下列函数图像
x ... -2 -1 0 1 2 ...
... ...
... ...
x ... -2 -1 0 1 2 ...
... ...
... ...
探究:指数函数的图象与性质
2
4
3
9
4
2
9
3
1
1
1
1
探究:指数函数的图象与性质
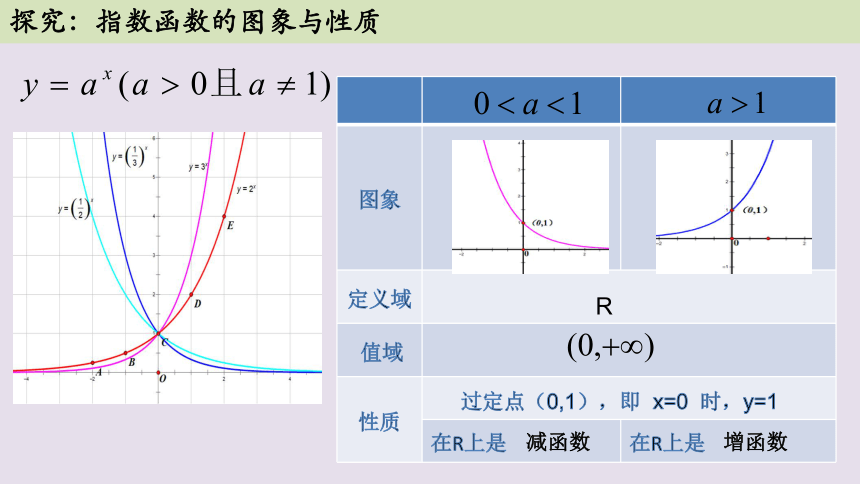
探究:指数函数的图象与性质
图象
定义域
值域
性质
在R上是 在R上是
R
过定点(0,1),即 x=0 时,y=1
减函数
增函数
探究:指数函数的图象与性质
探究:指数函数的图象与性质
减
②
例1.比较下列各题中两个值的大小。
指数函数的图象与性质的应用
同类练:比较下列各题中两值的大小。
例2. 如图4.2-7,某城市人口呈指数增长.
(1)根据图象,估计该城市人口每翻一番所需的时间(倍增期);
(2)该城市人口从80万人开始,经过20年会增长到多少万人?
例1.比较下列各题中两个值的大小。
指数函数的图象与性质的应用
解:
同类练:比较下列各题中两值的大小。
指数函数的图象与性质的应用
指数函数的图象与性质的应用
例2 如图4.2-7,某城市人口呈指数增长.
(1)根据图象,估计该城市人口每翻一番所需的时间(倍增期);
(2)该城市人口从80万人开始,经过20年会增长到多少万人?
解:(1)观察图4.3-7,发现该城市人口经过20年约为10万人,经过40年约为20万人,即由10万人口增加到20 万人口所用的时间约为20年,所以该城市人口每翻一番所需的时间约为20年.
解:(2)因为倍增期为20年,所以每经过20年, 人口将翻一番.因此,从80万人开始,经过20年, 该城市人口大约会增长到160万人.
课堂总结
图象
定义域
值域
性质
在R上是 在R上是
R
过定点(0,1),即 x=0 时,y=1
减函数
增函数
数形结合
分类讨论
特殊到一般
... ...
当堂检测
B
A
(-1,-1)
必做题:课本118页练习1,2题,119页6,7题
选做题:课本120页10题
课后作业
努力拼搏!无悔青春!不负韶华!
教学阐释
第二部分
学情分析
教材分析
教学目标
教学过程
方法策略
学情分析
前面幂函数的学习提供了“背景—概念—图象和性质—应用”的学习思路;学生初步掌握函数的基本性质、简单的指数运算以及用描点法作函数图象等;也从上节课学习中了解了指数函数是描述变化率的增长或衰减的一种函数模型;这都有助于学生对指数函数图象与性质的理解和掌握。而不同底数的指数函数图象及其联系对学生来说是一个难点,需要学生实操并借助信息技术手段加以突破。此外,学生的思维严谨性以及分类讨论、归纳概括等能力有待提升,要鼓励学生积极思考探索。
教材分析
本节课是人教A版(2019版)高中数学必修一第四章《指数函数与对数函数》第二节《指数函数》中基于函数的概念进一步研究其图像和性质,从而深化学生对函数的理解,使学生得到较为全面系统的函数知识和研究函数的方法,也为以后研究对数函数等其它函数打下坚实基础。
01
这节课具体内容是指数函数的图象与性质,探索学习过程实现课程标准要求的“③能用描点法或借助计算工具画出具体指数函数的图象,探索并理解指数函数的单调性与特殊点。”。
02
教学目标
课程目标
1.掌握指数函数的图象以及函数图象随参数变化而变化的规律;
2.能从具体的指数函数图象,推广到一般指数函数的图象规律进而得到指数函数的性质,培养学生特殊到一般、数形结合、分类讨论的数学思想;
素养目标
培养学生数学抽象、逻辑推理、数学运算、数据分析、数学建模的学科素养
重点 指数函数的图象及性质
难点 指数函数的性质中对底数的分类
教学过程
课前准备
课堂学习
课后整理
课前准备
课堂学习
作图观察
构建新知
辨析理解
深化概念
温习旧识
明确目标
02
03
04
05
06
当堂检测
作业布置
07
梳理课堂
归纳总结
新知应用
巩固内化
创设情境
导入新课
01
用
3
1
2
4
辨
引
识
问题
独立思考
组间交流
动脑
动手
动口
组内交流
成果展示
课后整理
导学案
学习评价表
作业批改
教学反思
方法策略
本节课的教学坚持以“学生为主体”的基本理念,尊重学生的认知规律,调动学生的主观能动性,通过先学后教、操作确认、归纳概括、辨析理解、应用训练等方法与策略。引导学生收获知识与能力!
心中有学生
眼中有学生
言中有学生
4.2.2指数函数的图象与性质(1)
第四章 指数函数与对数函数
人教A版 必修一
课堂展示
第一部分
4.2.2指数函数的图象与性质(1)
第四章 指数函数与对数函数
人教A版 必修一
学习目标 1.掌握指数函数的图象以及函数图象随参数变化而变化的规律;
2.能从具体的指数函数图象,推广到一般指数函数的图象规律
进而得到指数函数的性质,体会特殊到一般、数形结合、分类
讨论的数学思想;.
3. 提升数学抽象、逻辑推理、数学运算、数据分析等数学学科
素养。
学习重点 指数函数的图象及其随参数变化而变化的规律
学习难点 对底数的分类,如何由图象、解析式归纳指数函数的性质
学习目标、重难点
课前小测
C
[1,+∞)
指数函数
一般地,函数 叫做指数函数。
其中指数x是自变量,定义域是R。
任务:用描点法在同一坐标系作出下列函数图像
x ... -2 -1 0 1 2 ...
... ...
... ...
x ... -2 -1 0 1 2 ...
... ...
... ...
探究:指数函数的图象与性质
2
4
3
9
4
2
9
3
1
1
1
1
探究:指数函数的图象与性质
探究:指数函数的图象与性质
图象
定义域
值域
性质
在R上是 在R上是
R
过定点(0,1),即 x=0 时,y=1
减函数
增函数
探究:指数函数的图象与性质
探究:指数函数的图象与性质
减
②
例1.比较下列各题中两个值的大小。
指数函数的图象与性质的应用
同类练:比较下列各题中两值的大小。
例2. 如图4.2-7,某城市人口呈指数增长.
(1)根据图象,估计该城市人口每翻一番所需的时间(倍增期);
(2)该城市人口从80万人开始,经过20年会增长到多少万人?
例1.比较下列各题中两个值的大小。
指数函数的图象与性质的应用
解:
同类练:比较下列各题中两值的大小。
指数函数的图象与性质的应用
指数函数的图象与性质的应用
例2 如图4.2-7,某城市人口呈指数增长.
(1)根据图象,估计该城市人口每翻一番所需的时间(倍增期);
(2)该城市人口从80万人开始,经过20年会增长到多少万人?
解:(1)观察图4.3-7,发现该城市人口经过20年约为10万人,经过40年约为20万人,即由10万人口增加到20 万人口所用的时间约为20年,所以该城市人口每翻一番所需的时间约为20年.
解:(2)因为倍增期为20年,所以每经过20年, 人口将翻一番.因此,从80万人开始,经过20年, 该城市人口大约会增长到160万人.
课堂总结
图象
定义域
值域
性质
在R上是 在R上是
R
过定点(0,1),即 x=0 时,y=1
减函数
增函数
数形结合
分类讨论
特殊到一般
... ...
当堂检测
B
A
(-1,-1)
必做题:课本118页练习1,2题,119页6,7题
选做题:课本120页10题
课后作业
努力拼搏!无悔青春!不负韶华!
教学阐释
第二部分
学情分析
教材分析
教学目标
教学过程
方法策略
学情分析
前面幂函数的学习提供了“背景—概念—图象和性质—应用”的学习思路;学生初步掌握函数的基本性质、简单的指数运算以及用描点法作函数图象等;也从上节课学习中了解了指数函数是描述变化率的增长或衰减的一种函数模型;这都有助于学生对指数函数图象与性质的理解和掌握。而不同底数的指数函数图象及其联系对学生来说是一个难点,需要学生实操并借助信息技术手段加以突破。此外,学生的思维严谨性以及分类讨论、归纳概括等能力有待提升,要鼓励学生积极思考探索。
教材分析
本节课是人教A版(2019版)高中数学必修一第四章《指数函数与对数函数》第二节《指数函数》中基于函数的概念进一步研究其图像和性质,从而深化学生对函数的理解,使学生得到较为全面系统的函数知识和研究函数的方法,也为以后研究对数函数等其它函数打下坚实基础。
01
这节课具体内容是指数函数的图象与性质,探索学习过程实现课程标准要求的“③能用描点法或借助计算工具画出具体指数函数的图象,探索并理解指数函数的单调性与特殊点。”。
02
教学目标
课程目标
1.掌握指数函数的图象以及函数图象随参数变化而变化的规律;
2.能从具体的指数函数图象,推广到一般指数函数的图象规律进而得到指数函数的性质,培养学生特殊到一般、数形结合、分类讨论的数学思想;
素养目标
培养学生数学抽象、逻辑推理、数学运算、数据分析、数学建模的学科素养
重点 指数函数的图象及性质
难点 指数函数的性质中对底数的分类
教学过程
课前准备
课堂学习
课后整理
课前准备
课堂学习
作图观察
构建新知
辨析理解
深化概念
温习旧识
明确目标
02
03
04
05
06
当堂检测
作业布置
07
梳理课堂
归纳总结
新知应用
巩固内化
创设情境
导入新课
01
用
3
1
2
4
辨
引
识
问题
独立思考
组间交流
动脑
动手
动口
组内交流
成果展示
课后整理
导学案
学习评价表
作业批改
教学反思
方法策略
本节课的教学坚持以“学生为主体”的基本理念,尊重学生的认知规律,调动学生的主观能动性,通过先学后教、操作确认、归纳概括、辨析理解、应用训练等方法与策略。引导学生收获知识与能力!
心中有学生
眼中有学生
言中有学生
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
