11.1.2 三角形的高、中线与角平分线同步练习题(含答案)
文档属性
| 名称 | 11.1.2 三角形的高、中线与角平分线同步练习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-10 07:16:20 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
11.1.2三角形的高、中线与角平分线
学校:______姓名:______班级:______考号:______
一、单选题
1.三角形三条中线的交点叫做三角形的( )
A.内心 B.外心 C.中心 D.重心
2.下列说法正确的是( ).
A.三角形的角平分线、中线、高都在三角形的内部
B.直角三角形只有一条高
C.三角形的三条高至少有一条在三角形内
D.钝角三角形的三条高均在三角形外
3.如图,中高和的交点为则等于( )
A. B. C. D.
4.如图,,分别是的边,的中点,那么下列说法中不正确的是( )
A.是的中线 B.是的中线
C., D.,
5.如图在中,是的中点,,则是( )
A. B. C. D.
6.如图所示,在中,点在上,且是的中点,交于点连结则下列说法正确的是( )
①是的角平分线;
②是的边上的中线;
③是的中线;
④是的中线;
⑤是的角平分线;
⑥是的中线.
A.①②④ B.①④⑤⑥ C.②⑤⑥ D.①③⑤
7.如图,在中是上的一点是的中点的面积分别记为且则的值为( )
A. B. C. D.
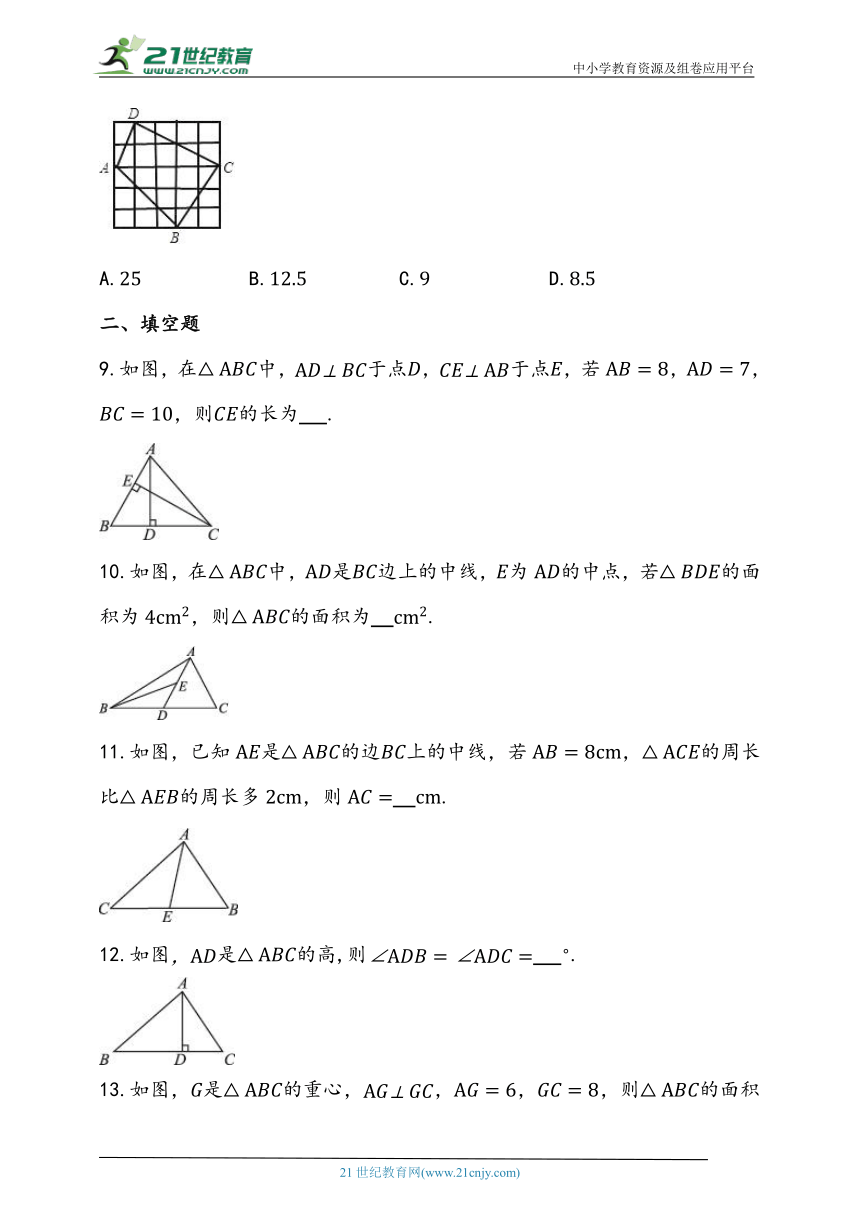
8.如图,小方格都是边长为的正方形,则四边形的面积是( )
A. B. C. D.
二、填空题
9.如图,在中,于点,于点,若,,,则的长为 .
10.如图,在中,是边上的中线,为的中点,若的面积为,则的面积为 .
11.如图,已知是的边上的中线,若,的周长比的周长多,则 .
12.如图是的高,则 .
13.如图,是的重心,,,,则的面积为 .
14.如图,中,,,,,垂足分别为,,,则线段 是中边上的高.
15.已知,如图,于点,于点,与交于点的边上的高为 ,这上的高为 .
三、解答题
16.如图,在中分别是边上的中线.若且的周长为求的长.
17.如图,在中,为边上的中线,为边上的高.若,的面积为,求的长.
18.如图,在中,,,分别是,的平分线且相交于点,求的度数.
19.如图,在直角三角形中,,是边上的高,,,求:
(1)的面积;
(2)的长;
(3)作出的边上的中线,并求出的面积;
(4)作出的边边上的高,当时,试求出的长.
参考答案
1.【答案】D
【解析】根据三角形的重心概念作出回答,结合选项得出结果.
三角形的重心是三角形三条中线的交点.
故选D.
2.【答案】C
【解析】【分析】本题考查了对三角形的中线、角平分线、高概念的理解特别注意不同形状的三角形三条线段的位置不同根据三角形的角平分线、中线、高的概念对每一个选项进行判断即可.
【解答】
解:三角形的三条高不一定都在三角形的内部,故此选项错误;
直角三角形有两条高就是两条直角边,故此选项错误;
锐角三角形的三条高都在内部;直角三角形有两条高是直角边,另一条高在内部;钝角三角形有两条高在外部,一条在内部,故此选项正确;
钝角三角形有两条高在外部,一条在内部,故此选项错误.
故选.
3.【答案】C
4.【答案】D
【解析】根据中线的定义可知选项,,正确.
5.【答案】B
【解析】【分析】根据是的中线,于是得到结论.
【解答】解:∵是的中点,
∴是的中线,
∴ ,
故选.
6.【答案】B
7.【答案】B
8.【答案】B
【解析】如图:小方格都是边长为的正方形,
∴四边形是正方形,
,
,
,
.
.
故选:.
解答此题的关键在于理解三角形的面积的相关知识,掌握 三角形的面积底高.{}
9.【答案】
【解析】因为,,
所以,
所以,
所以,
所以.
10.【答案】
11.【答案】
【解析】是的边上的中线,
.
又,的周长比的周长多,
.
又
.
故答案为.
12.【答案】
13.【答案】
【解析】如图,延长交于点.
,,,
的面积.
是的重心,
,
的面积的面积,
的面积.
是的中线,
的面积为. 故答案为.
14.【答案】
15.【答案】;
【解析】【分析】
本题主要考查了高的定义 根据高的定义可知,的边上的高为,边上的高为.
【解答】
解:的边上的高为,边上的高为.
故答案为;.
16.【答案】解:分别是边上的中线,
.
的周长为
17.【答案】解:因为为边上的中线,
所以,
所以.
因为,,
所以,
所以.
18.【答案】
【解析】 分别是的角平分线,
在中,
故答案为:140°.
19.【答案】(1)解:,,,
,
(2),
,
(3)如图,
,
(4)如图,
,
,
,
.
【解析】(1)根据直角三角形面积的求法,即可得出的面积,
(2)根据三角形的面积公式即可求得的长,
(3)根据中线的性质可得出和的面积相等,从而得出答案,
(4)过点作垂直于交与,根据的面积即可求出本题考查了勾股定理的逆定理、直角三角形的面积的计算方法及面积公式应用同时考查了直角三角形的高、中点的性质,难度适中.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
11.1.2三角形的高、中线与角平分线
学校:______姓名:______班级:______考号:______
一、单选题
1.三角形三条中线的交点叫做三角形的( )
A.内心 B.外心 C.中心 D.重心
2.下列说法正确的是( ).
A.三角形的角平分线、中线、高都在三角形的内部
B.直角三角形只有一条高
C.三角形的三条高至少有一条在三角形内
D.钝角三角形的三条高均在三角形外
3.如图,中高和的交点为则等于( )
A. B. C. D.
4.如图,,分别是的边,的中点,那么下列说法中不正确的是( )
A.是的中线 B.是的中线
C., D.,
5.如图在中,是的中点,,则是( )
A. B. C. D.
6.如图所示,在中,点在上,且是的中点,交于点连结则下列说法正确的是( )
①是的角平分线;
②是的边上的中线;
③是的中线;
④是的中线;
⑤是的角平分线;
⑥是的中线.
A.①②④ B.①④⑤⑥ C.②⑤⑥ D.①③⑤
7.如图,在中是上的一点是的中点的面积分别记为且则的值为( )
A. B. C. D.
8.如图,小方格都是边长为的正方形,则四边形的面积是( )
A. B. C. D.
二、填空题
9.如图,在中,于点,于点,若,,,则的长为 .
10.如图,在中,是边上的中线,为的中点,若的面积为,则的面积为 .
11.如图,已知是的边上的中线,若,的周长比的周长多,则 .
12.如图是的高,则 .
13.如图,是的重心,,,,则的面积为 .
14.如图,中,,,,,垂足分别为,,,则线段 是中边上的高.
15.已知,如图,于点,于点,与交于点的边上的高为 ,这上的高为 .
三、解答题
16.如图,在中分别是边上的中线.若且的周长为求的长.
17.如图,在中,为边上的中线,为边上的高.若,的面积为,求的长.
18.如图,在中,,,分别是,的平分线且相交于点,求的度数.
19.如图,在直角三角形中,,是边上的高,,,求:
(1)的面积;
(2)的长;
(3)作出的边上的中线,并求出的面积;
(4)作出的边边上的高,当时,试求出的长.
参考答案
1.【答案】D
【解析】根据三角形的重心概念作出回答,结合选项得出结果.
三角形的重心是三角形三条中线的交点.
故选D.
2.【答案】C
【解析】【分析】本题考查了对三角形的中线、角平分线、高概念的理解特别注意不同形状的三角形三条线段的位置不同根据三角形的角平分线、中线、高的概念对每一个选项进行判断即可.
【解答】
解:三角形的三条高不一定都在三角形的内部,故此选项错误;
直角三角形有两条高就是两条直角边,故此选项错误;
锐角三角形的三条高都在内部;直角三角形有两条高是直角边,另一条高在内部;钝角三角形有两条高在外部,一条在内部,故此选项正确;
钝角三角形有两条高在外部,一条在内部,故此选项错误.
故选.
3.【答案】C
4.【答案】D
【解析】根据中线的定义可知选项,,正确.
5.【答案】B
【解析】【分析】根据是的中线,于是得到结论.
【解答】解:∵是的中点,
∴是的中线,
∴ ,
故选.
6.【答案】B
7.【答案】B
8.【答案】B
【解析】如图:小方格都是边长为的正方形,
∴四边形是正方形,
,
,
,
.
.
故选:.
解答此题的关键在于理解三角形的面积的相关知识,掌握 三角形的面积底高.{}
9.【答案】
【解析】因为,,
所以,
所以,
所以,
所以.
10.【答案】
11.【答案】
【解析】是的边上的中线,
.
又,的周长比的周长多,
.
又
.
故答案为.
12.【答案】
13.【答案】
【解析】如图,延长交于点.
,,,
的面积.
是的重心,
,
的面积的面积,
的面积.
是的中线,
的面积为. 故答案为.
14.【答案】
15.【答案】;
【解析】【分析】
本题主要考查了高的定义 根据高的定义可知,的边上的高为,边上的高为.
【解答】
解:的边上的高为,边上的高为.
故答案为;.
16.【答案】解:分别是边上的中线,
.
的周长为
17.【答案】解:因为为边上的中线,
所以,
所以.
因为,,
所以,
所以.
18.【答案】
【解析】 分别是的角平分线,
在中,
故答案为:140°.
19.【答案】(1)解:,,,
,
(2),
,
(3)如图,
,
(4)如图,
,
,
,
.
【解析】(1)根据直角三角形面积的求法,即可得出的面积,
(2)根据三角形的面积公式即可求得的长,
(3)根据中线的性质可得出和的面积相等,从而得出答案,
(4)过点作垂直于交与,根据的面积即可求出本题考查了勾股定理的逆定理、直角三角形的面积的计算方法及面积公式应用同时考查了直角三角形的高、中点的性质,难度适中.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
