福建省龙岩市2022-2023学年高二下学期期末教学质量检查数学试题(Word版含答案)
文档属性
| 名称 | 福建省龙岩市2022-2023学年高二下学期期末教学质量检查数学试题(Word版含答案) | 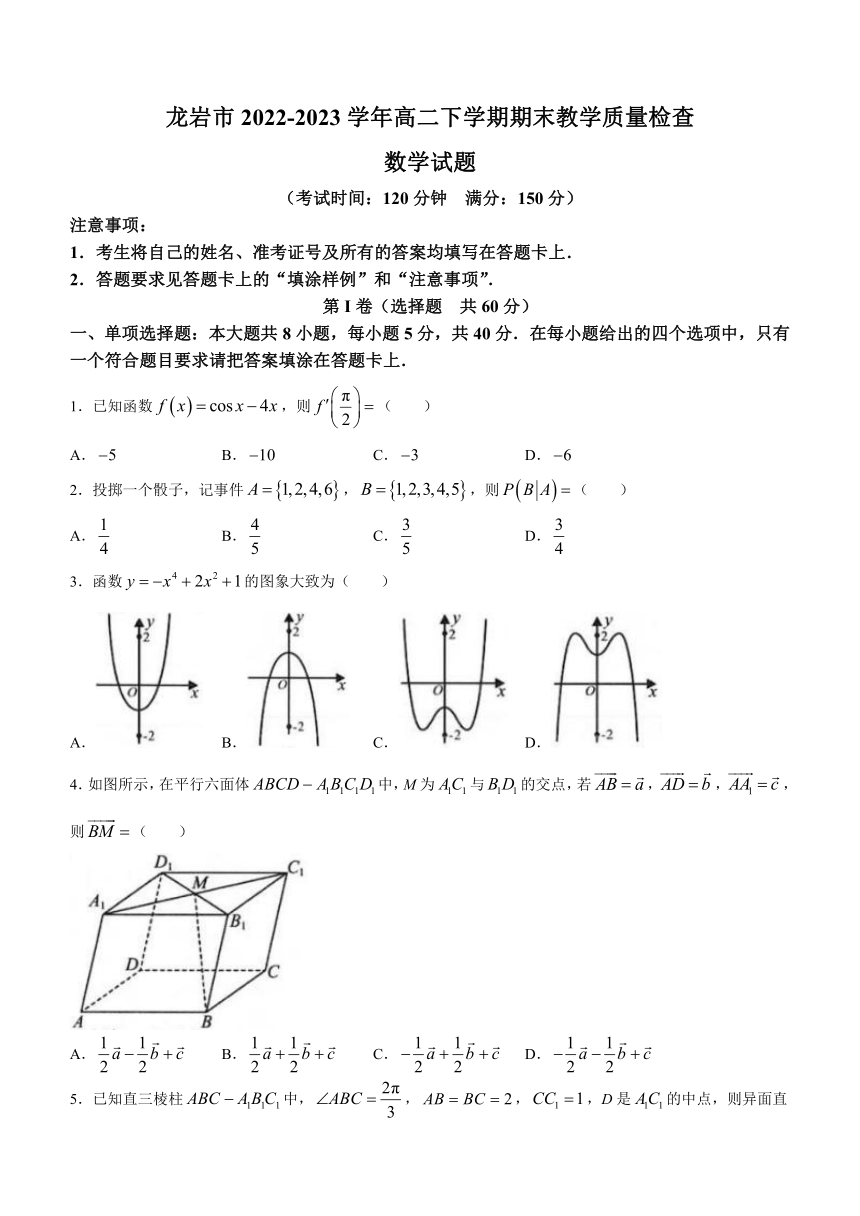 | |
| 格式 | docx | ||
| 文件大小 | 945.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-09 23:36:11 | ||
图片预览




文档简介
龙岩市2022-2023学年高二下学期期末教学质量检查
数学试题
(考试时间:120分钟 满分:150分)
注意事项:
1.考生将自己的姓名、准考证号及所有的答案均填写在答题卡上.
2.答题要求见答题卡上的“填涂样例”和“注意事项”.
第I卷(选择题 共60分)
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个符合题目要求请把答案填涂在答题卡上.
1.已知函数,则( )
A. B. C. D.
2.投掷一个骰子,记事件,,则( )
A. B. C. D.
3.函数的图象大致为( )
A. B. C. D.
4.如图所示,在平行六面体中,M为与的交点,若,,,则( )
A. B. C. D.
5.已知直三棱柱中,,,,D是的中点,则异面直线与CD所成角的余弦值为( )
A. B. C. D.
6.已知甲、乙盒子各装有形状大小完全相同的小球,其中甲盒子内有2个红球,1个白球;乙盒子内有3个红球,2个白球.若第一次先从甲盒子内随机抽取1个球放入乙盒子中,则第二次从乙盒子中抽1个球是红球的概率为( )
A. B. C. D.
7.,,,则不等式的解集为( )
A. B. C. D.
8.若,,,则( )
A. B. C. D.
二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.请把答案填涂在答题卡上.
9.下列说法正确的是( )
A.两个随机变量的线性相关性越强,相关系数的绝对值越接近于1
B.运用最小二乘法求得的回归直线一定经过样本中心
C.在一个列联表中,计算得到的值,若的值越小,则可以判断两个变量有关的概率越大
D.利用独立性检验推断“A与B是否有关”,根据数据算得,已知,,则有超过97.5%的把握认为A与B无关
10.若函数在区间内有最小值,则实数m的取值可能为( )
A. B. C. D.
11.已知函数则下列选项正确的是( )
A.函数的值域为
B.函数的单调减区间为,
C.若关于x的方程有3个不相等的实数根,则实数a的取值范围是
D.若关于x的方程有6个不相等的实数根,则实数a的取值范围是
12.在棱长为2的正方体中,点N满足,其中,,异面直线BN与所成角为,点M满足,则下列选项正确的是( )
A.
B.
C.当线段MN取最小值时,
D.当时,与AM垂直的平面截正方体所得的截面面积最大值为
第II卷(非选择题 共90分)
三、填空题:本大题共4小题,每小题5分,共20分.
13.已知空间向量,,若,则________.
14.英国数学家贝叶斯在概率论研究方面成就显著,根据贝叶斯统计理论,随机事件A,B有如下关系:.某地有A,B两个游泳馆,甲同学决定周末两天都去游泳馆游泳,周六选择A,B游泳馆的概率均为0.5.如果甲同学周六去A馆,那么周日还去A馆的概率为0.4;如果周六去B馆,那么周日去A馆的概率为0.8.如果甲同学周日去A馆游泳,则他周六去A馆游泳的概率为________.
15.在棱长为2的正方体中,P是侧面上的动点,且满足,则的最小值为________.
16.函数,若不等式恒成立,则实数a的取值范围为________.
四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本题满分10分)
已知函数.
(1)若,求函数在点处的切线方程;
(2)若函数在处取得极值,求的单调区间.
18.(本题满分12分)
如图,在四棱锥中,底面ABCD,,,,,点E为棱PC的中点.
(1)求证:平面PAD;
(2)求直线BE与平面PBD所成角的正弦值.
19.(本题满分12分)
第22届亚运会将于2023年9月23日至10月8日在我国杭州举行.为了让中学生了解亚运会,某市举办了一次亚运会知识竞赛,分预赛和复赛两个环节,现从参加预赛的全体学生中随机抽取100人的预赛成绩作为样本,得到频率分布表(见右表).
分组(百分制) 频数 频率
10 0.1
20 0.2
30 0.3
25 0.25
15 0.15
合计 100 1
(1)由频率分布表可认为该市全体参加预赛学生的预赛成绩X服从正态分布,其中可近似为样本中的100名学生预赛成绩的平均值(同一组数据用该组区间的中点值代替),且.利用该正态分布,求;
(2)预赛成绩不低于80分的学生将参加复赛,现用样本估计总体,将频率视为概率.从该市参加预赛的学生中随机抽取2人,记进人复赛的人数为Y,求Y的概率分布列和数学期望.
附:若,则,,;.
20.(本题满分12分)
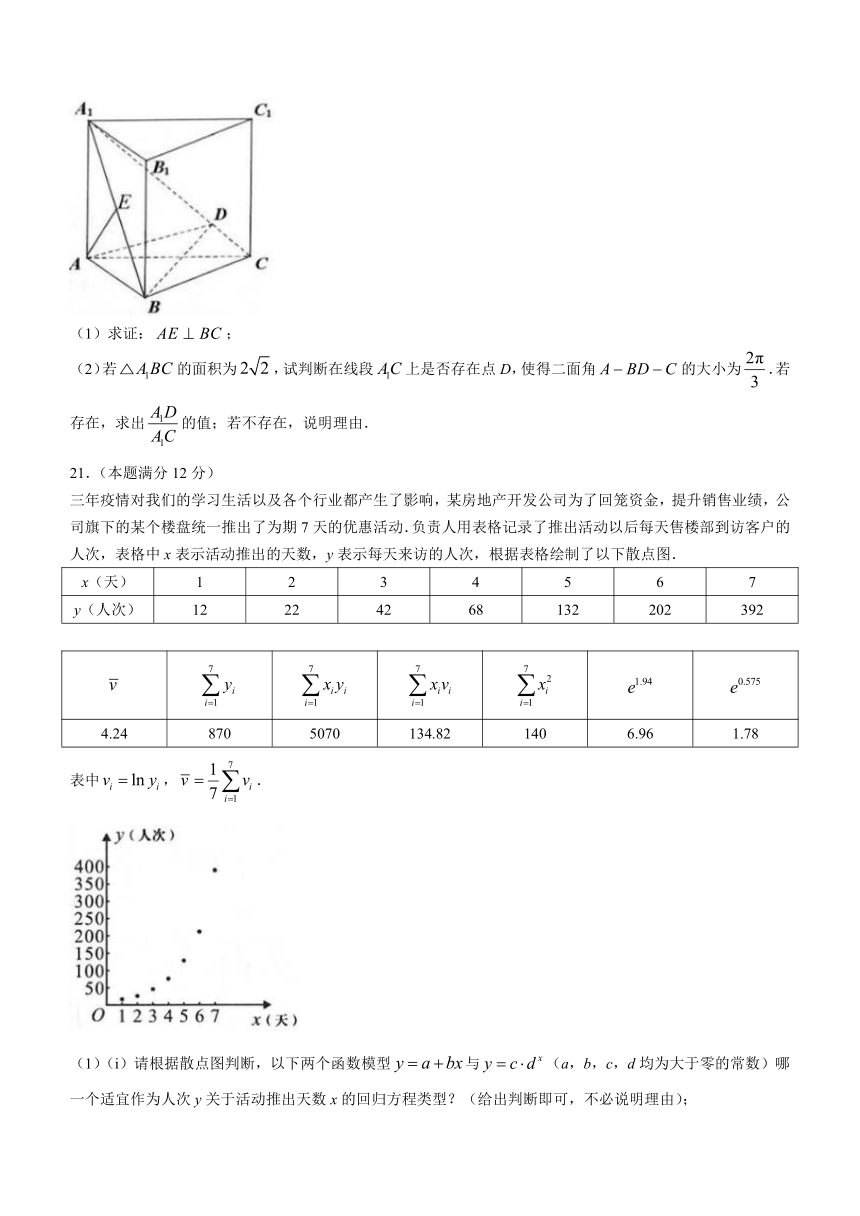
如图,在直三棱柱中,,E为的中点,平面平面.
(1)求证:;
(2)若的面积为,试判断在线段上是否存在点D,使得二面角的大小为.若存在,求出的值;若不存在,说明理由.
21.(本题满分12分)
三年疫情对我们的学习生活以及各个行业都产生了影响,某房地产开发公司为了回笼资金,提升销售业绩,公司旗下的某个楼盘统一推出了为期7天的优惠活动.负责人用表格记录了推出活动以后每天售楼部到访客户的人次,表格中x表示活动推出的天数,y表示每天来访的人次,根据表格绘制了以下散点图.
x(天) 1 2 3 4 5 6 7
y(人次) 12 22 42 68 132 202 392
4.24 870 5070 134.82 140 6.96 1.78
表中,.
(1)(i)请根据散点图判断,以下两个函数模型与(a,b,c,d均为大于零的常数)哪一个适宜作为人次y关于活动推出天数x的回归方程类型?(给出判断即可,不必说明理由);
(ii)根据(i)的判断结果以及表中的数据,求y关于x的回归方程.
(2)此楼盘共有N套房,其中200套特价房,活动期间共卖出300套房,其中50套特价房,试给出N的估计值(以使得最大的N的值作为N的估计值,X表示卖出的300套房中特价房的数目).
附:对于样本(,2,…,n),其回归直线的斜率和截距的最小二乘估计公式分别为:.
22.(本题满分12分)
已知函数.
(1)讨论的单调性;
(2)已知,且,是的两个零点,,证明:.
龙岩市2022-2023学年高二下学期期末教学质量检查
数学参考答案
一、选择题(本大题共8小题,每小题5分,共40分).
题号 1 2 3 4 5 6 7 8
答案 A D D C B C D B
第7题简析:,令,所以,所以,又,所以,又,所以,所以.
第8题简析:因为,构造,易得:,所以,又易得,令,得,所以,即,所以,综上.
二、多项选择题(本大题共4小题,每小题5分,共20分)
题号 9 10 11 12
答案 AB CD ABD BCD
第11题简析:作出函数的图象,由图象可知A正确,B正确
对于C选项或,由函数的图象可知或,故C错误.
对于D选项或,由函数的图象可知
第12题简析:由题意知点在上动点,点的轨迹为以为圆心,为半径的圆弧,所以,所以A错误;
易得平面,所以,所以B正确;
当线段取最小值时,是的中点,为圆弧的中点,所以,所以,所以,所以C正确;
当时,与重合,与垂直的平面,即与体对角线垂直的平面,显然平面,而与平面平行且面积最大的截面应当过正方体的中心,此时截面为边长是的正六边形,所以截面面积的最大值为,所以D正确.
三、填空题(本大题共4小题,每小题5分,共20分)
13. 14. 15. 16.
第16题简析:法一:依题意:在上恒成立,
设,
令,,则在上单调递增,,,所以使,
当时,在单调递减;当时,在单调递增,,由得,设,则,在上单调递增,所以,即,故,所以
法二:,可证,当且仅当时取“”,令,即
当,即时,,此时不等式恒成立;
当,即时,设,在上单调递增,,,使,
即,与恒成立矛盾,故舍去,综上,.
四、解答题(本大题共6小题,共70分)
17.(本题满分10分)
解:(1)因为所以.
所以,……1分
所以,……2分
又,
所以曲线在点处的切线方程为:.……4分
(2)由函数在处取得极值可知:
,即,解得:.……6分
此时,,,
当时,,
当时,,
所以符合题意.
综上,的单调递增区间为,的单调递减区间为.
……10分
18.(本题满分12分)
证明:(1)证明:如图所示,取中点,连接.……1分
分别为的中点,
,且.
又由已知,可得且,
四边形为平行四边形,
..……3分
又平面,平面.
平面.……4分
(2)如图,以点为原点建立空间直角坐标系,……5分
则.
由为棱的中点,得.
向量,.
设为平面的法向量,
则.
不妨令,得,即为平面的一个法向量.……8分
又向量,
设直线与平面所成角为,
.……11分
直线与平面所成角的正弦值为.……12分
19.(本题满分12分)
解:(1)由题意知样本中的100名学生预赛成绩的平均值为:
,……2分
又由,,
.
……5分
(2)由题意,抽取2人进入复赛的人数,……6分
.
的概率分布列为
0 1 2
……10分
的数学期望为.……12分
20.(本题满分12分)
解:(1)如图,在直三棱柱中,
,∴矩形为正方形,
又E是的中点,
.……1分
又平面平面,
平面平面,
且平面.
平面.……3分
又平面,
.……4分
(2)在直三棱柱中,平面.
又平面,
.
又,
平面且相交,
平面.
所以两两垂直.
所以如图以为原点,建立空间直角坐标系.……6分
的面积为,
.
则,
.
设,
.
又,
设平面的法向量,
则,
不妨取,则,
∴,……8分
由(1)平面,∴平面的一个法向量,……9分
.……11分
解得.
又由图可知当为的中点时,二面角为钝二面角符合题意,
综上,在上存在一点D,此时,
使得二面角的大小为.……12分
21.(本题满分12分)
解:(1)(ⅰ)根据散点图可得随的增大,增长速度越来越快,不满足线性回归,故判断适合作为人次关于活动推出天数的回归方程类型.……2分
(ⅱ)由(ⅰ)知,,两边同时取对数得,
令.则由题意知,
又,
所以,
所以,所以,……4分
,,
则关于的回归方程为.……6分
(2)依题意服从超几何分布,
当时,,
当时,,记,……8分
则,
由解得,……10分
所以当时,
当时,
当时,
故当或时最大,所以的估计值为.……12分
22.(本题满分12分)
解:(1),……1分
①若,则,即在单调递减,
②若,令,有,令,有,
即在单调递减,在单调递增,……3分
综上:,在单调递减,
若,在单调递减,在单调递增.……4分
(2),
令得:,
因为,,因为是的两个零点,
所以,,……6分
所以,
,……7分
要证明,
只需证,
即证明
变形为,令,
则证明,……9分
设,,在单调递增,
所以,即,
设,,在单调递减,
所以,,即,,
综上:.……12分
数学试题
(考试时间:120分钟 满分:150分)
注意事项:
1.考生将自己的姓名、准考证号及所有的答案均填写在答题卡上.
2.答题要求见答题卡上的“填涂样例”和“注意事项”.
第I卷(选择题 共60分)
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个符合题目要求请把答案填涂在答题卡上.
1.已知函数,则( )
A. B. C. D.
2.投掷一个骰子,记事件,,则( )
A. B. C. D.
3.函数的图象大致为( )
A. B. C. D.
4.如图所示,在平行六面体中,M为与的交点,若,,,则( )
A. B. C. D.
5.已知直三棱柱中,,,,D是的中点,则异面直线与CD所成角的余弦值为( )
A. B. C. D.
6.已知甲、乙盒子各装有形状大小完全相同的小球,其中甲盒子内有2个红球,1个白球;乙盒子内有3个红球,2个白球.若第一次先从甲盒子内随机抽取1个球放入乙盒子中,则第二次从乙盒子中抽1个球是红球的概率为( )
A. B. C. D.
7.,,,则不等式的解集为( )
A. B. C. D.
8.若,,,则( )
A. B. C. D.
二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.请把答案填涂在答题卡上.
9.下列说法正确的是( )
A.两个随机变量的线性相关性越强,相关系数的绝对值越接近于1
B.运用最小二乘法求得的回归直线一定经过样本中心
C.在一个列联表中,计算得到的值,若的值越小,则可以判断两个变量有关的概率越大
D.利用独立性检验推断“A与B是否有关”,根据数据算得,已知,,则有超过97.5%的把握认为A与B无关
10.若函数在区间内有最小值,则实数m的取值可能为( )
A. B. C. D.
11.已知函数则下列选项正确的是( )
A.函数的值域为
B.函数的单调减区间为,
C.若关于x的方程有3个不相等的实数根,则实数a的取值范围是
D.若关于x的方程有6个不相等的实数根,则实数a的取值范围是
12.在棱长为2的正方体中,点N满足,其中,,异面直线BN与所成角为,点M满足,则下列选项正确的是( )
A.
B.
C.当线段MN取最小值时,
D.当时,与AM垂直的平面截正方体所得的截面面积最大值为
第II卷(非选择题 共90分)
三、填空题:本大题共4小题,每小题5分,共20分.
13.已知空间向量,,若,则________.
14.英国数学家贝叶斯在概率论研究方面成就显著,根据贝叶斯统计理论,随机事件A,B有如下关系:.某地有A,B两个游泳馆,甲同学决定周末两天都去游泳馆游泳,周六选择A,B游泳馆的概率均为0.5.如果甲同学周六去A馆,那么周日还去A馆的概率为0.4;如果周六去B馆,那么周日去A馆的概率为0.8.如果甲同学周日去A馆游泳,则他周六去A馆游泳的概率为________.
15.在棱长为2的正方体中,P是侧面上的动点,且满足,则的最小值为________.
16.函数,若不等式恒成立,则实数a的取值范围为________.
四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本题满分10分)
已知函数.
(1)若,求函数在点处的切线方程;
(2)若函数在处取得极值,求的单调区间.
18.(本题满分12分)
如图,在四棱锥中,底面ABCD,,,,,点E为棱PC的中点.
(1)求证:平面PAD;
(2)求直线BE与平面PBD所成角的正弦值.
19.(本题满分12分)
第22届亚运会将于2023年9月23日至10月8日在我国杭州举行.为了让中学生了解亚运会,某市举办了一次亚运会知识竞赛,分预赛和复赛两个环节,现从参加预赛的全体学生中随机抽取100人的预赛成绩作为样本,得到频率分布表(见右表).
分组(百分制) 频数 频率
10 0.1
20 0.2
30 0.3
25 0.25
15 0.15
合计 100 1
(1)由频率分布表可认为该市全体参加预赛学生的预赛成绩X服从正态分布,其中可近似为样本中的100名学生预赛成绩的平均值(同一组数据用该组区间的中点值代替),且.利用该正态分布,求;
(2)预赛成绩不低于80分的学生将参加复赛,现用样本估计总体,将频率视为概率.从该市参加预赛的学生中随机抽取2人,记进人复赛的人数为Y,求Y的概率分布列和数学期望.
附:若,则,,;.
20.(本题满分12分)
如图,在直三棱柱中,,E为的中点,平面平面.
(1)求证:;
(2)若的面积为,试判断在线段上是否存在点D,使得二面角的大小为.若存在,求出的值;若不存在,说明理由.
21.(本题满分12分)
三年疫情对我们的学习生活以及各个行业都产生了影响,某房地产开发公司为了回笼资金,提升销售业绩,公司旗下的某个楼盘统一推出了为期7天的优惠活动.负责人用表格记录了推出活动以后每天售楼部到访客户的人次,表格中x表示活动推出的天数,y表示每天来访的人次,根据表格绘制了以下散点图.
x(天) 1 2 3 4 5 6 7
y(人次) 12 22 42 68 132 202 392
4.24 870 5070 134.82 140 6.96 1.78
表中,.
(1)(i)请根据散点图判断,以下两个函数模型与(a,b,c,d均为大于零的常数)哪一个适宜作为人次y关于活动推出天数x的回归方程类型?(给出判断即可,不必说明理由);
(ii)根据(i)的判断结果以及表中的数据,求y关于x的回归方程.
(2)此楼盘共有N套房,其中200套特价房,活动期间共卖出300套房,其中50套特价房,试给出N的估计值(以使得最大的N的值作为N的估计值,X表示卖出的300套房中特价房的数目).
附:对于样本(,2,…,n),其回归直线的斜率和截距的最小二乘估计公式分别为:.
22.(本题满分12分)
已知函数.
(1)讨论的单调性;
(2)已知,且,是的两个零点,,证明:.
龙岩市2022-2023学年高二下学期期末教学质量检查
数学参考答案
一、选择题(本大题共8小题,每小题5分,共40分).
题号 1 2 3 4 5 6 7 8
答案 A D D C B C D B
第7题简析:,令,所以,所以,又,所以,又,所以,所以.
第8题简析:因为,构造,易得:,所以,又易得,令,得,所以,即,所以,综上.
二、多项选择题(本大题共4小题,每小题5分,共20分)
题号 9 10 11 12
答案 AB CD ABD BCD
第11题简析:作出函数的图象,由图象可知A正确,B正确
对于C选项或,由函数的图象可知或,故C错误.
对于D选项或,由函数的图象可知
第12题简析:由题意知点在上动点,点的轨迹为以为圆心,为半径的圆弧,所以,所以A错误;
易得平面,所以,所以B正确;
当线段取最小值时,是的中点,为圆弧的中点,所以,所以,所以,所以C正确;
当时,与重合,与垂直的平面,即与体对角线垂直的平面,显然平面,而与平面平行且面积最大的截面应当过正方体的中心,此时截面为边长是的正六边形,所以截面面积的最大值为,所以D正确.
三、填空题(本大题共4小题,每小题5分,共20分)
13. 14. 15. 16.
第16题简析:法一:依题意:在上恒成立,
设,
令,,则在上单调递增,,,所以使,
当时,在单调递减;当时,在单调递增,,由得,设,则,在上单调递增,所以,即,故,所以
法二:,可证,当且仅当时取“”,令,即
当,即时,,此时不等式恒成立;
当,即时,设,在上单调递增,,,使,
即,与恒成立矛盾,故舍去,综上,.
四、解答题(本大题共6小题,共70分)
17.(本题满分10分)
解:(1)因为所以.
所以,……1分
所以,……2分
又,
所以曲线在点处的切线方程为:.……4分
(2)由函数在处取得极值可知:
,即,解得:.……6分
此时,,,
当时,,
当时,,
所以符合题意.
综上,的单调递增区间为,的单调递减区间为.
……10分
18.(本题满分12分)
证明:(1)证明:如图所示,取中点,连接.……1分
分别为的中点,
,且.
又由已知,可得且,
四边形为平行四边形,
..……3分
又平面,平面.
平面.……4分
(2)如图,以点为原点建立空间直角坐标系,……5分
则.
由为棱的中点,得.
向量,.
设为平面的法向量,
则.
不妨令,得,即为平面的一个法向量.……8分
又向量,
设直线与平面所成角为,
.……11分
直线与平面所成角的正弦值为.……12分
19.(本题满分12分)
解:(1)由题意知样本中的100名学生预赛成绩的平均值为:
,……2分
又由,,
.
……5分
(2)由题意,抽取2人进入复赛的人数,……6分
.
的概率分布列为
0 1 2
……10分
的数学期望为.……12分
20.(本题满分12分)
解:(1)如图,在直三棱柱中,
,∴矩形为正方形,
又E是的中点,
.……1分
又平面平面,
平面平面,
且平面.
平面.……3分
又平面,
.……4分
(2)在直三棱柱中,平面.
又平面,
.
又,
平面且相交,
平面.
所以两两垂直.
所以如图以为原点,建立空间直角坐标系.……6分
的面积为,
.
则,
.
设,
.
又,
设平面的法向量,
则,
不妨取,则,
∴,……8分
由(1)平面,∴平面的一个法向量,……9分
.……11分
解得.
又由图可知当为的中点时,二面角为钝二面角符合题意,
综上,在上存在一点D,此时,
使得二面角的大小为.……12分
21.(本题满分12分)
解:(1)(ⅰ)根据散点图可得随的增大,增长速度越来越快,不满足线性回归,故判断适合作为人次关于活动推出天数的回归方程类型.……2分
(ⅱ)由(ⅰ)知,,两边同时取对数得,
令.则由题意知,
又,
所以,
所以,所以,……4分
,,
则关于的回归方程为.……6分
(2)依题意服从超几何分布,
当时,,
当时,,记,……8分
则,
由解得,……10分
所以当时,
当时,
当时,
故当或时最大,所以的估计值为.……12分
22.(本题满分12分)
解:(1),……1分
①若,则,即在单调递减,
②若,令,有,令,有,
即在单调递减,在单调递增,……3分
综上:,在单调递减,
若,在单调递减,在单调递增.……4分
(2),
令得:,
因为,,因为是的两个零点,
所以,,……6分
所以,
,……7分
要证明,
只需证,
即证明
变形为,令,
则证明,……9分
设,,在单调递增,
所以,即,
设,,在单调递减,
所以,,即,,
综上:.……12分
同课章节目录
