相似三角形的应用[下学期]
图片预览








文档简介
课件29张PPT。神秘的埃及金字塔走进生活! 探索自然!相似三角形的应用相似三角形的识别方法(1)两个角对应相等的两三角形相似(2)两边对应成比例且夹角相等的
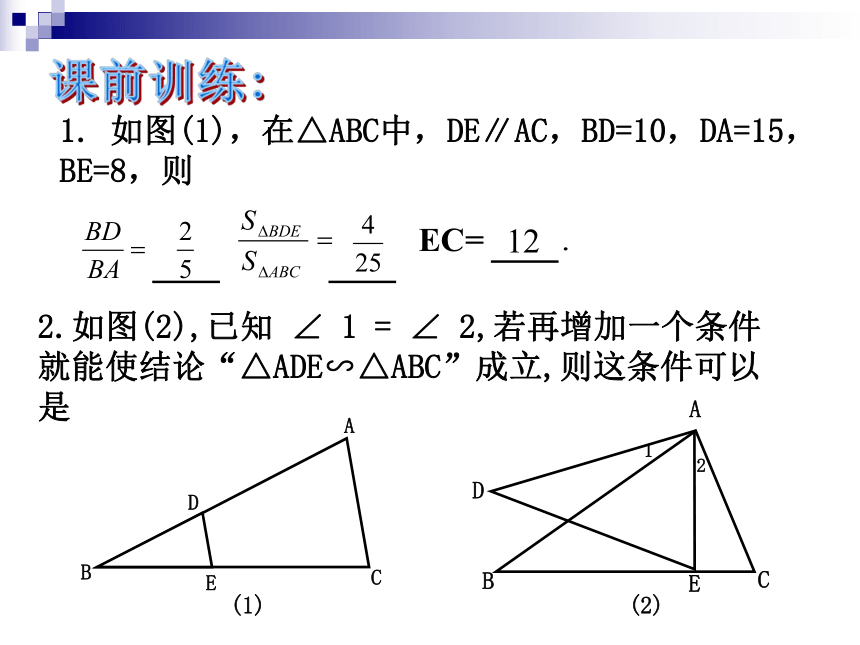
两三角形相似(3)三边对应成比例的两三角形相似复习相似三角形的性质6、相似三角形周长的比等于相似比5、相似三角形对应角平分线的比等于相似比复习4、相似三角形对应中线的比等于相似比7、相似三角形面积的比等于3、相似三角形对应高的比等于相似比1、相似三角形对应角相等2、相似三角形对应边成比例相似比的平方1. 如图(1),在△ABC中,DE∥AC,BD=10,DA=15,BE=8,则EC=
.课前训练:BDECA2.如图(2),已知 ∠ 1 = ∠ 2,若再增加一个条件就能使结论“△ADE∽△ABC”成立,则这条件可以是(1)ADBE(2)C12解:设楼的高度为x米,由题意得:
例1.在同一时刻物体的高度与它的影长成正比例.在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为60米,那么高楼的高度是多少米? 解得x=36(米)答:楼的高度是36米。 测量学校旗杆的高度。
古埃及所有金字塔中最大的一座是第四王朝法老胡夫王的金字塔。这座大金字塔原高146.59m,经过几千年的风吹雨打,顶端被风化吹蚀了近10m。在巴黎埃菲尔铁塔完成之前,它一直是世界上最高的建筑物。这座金字塔的底面呈正方形,边长大约230m。但由于经过几千年的风吹雨打,顶端被风化吹蚀.所以高度有所降低 。 走近金字塔小小考古家: 埃及著名的考古专家穆罕穆德决定重新测量胡夫金字塔的高度.在一个烈日高照的上午.他和儿子小穆罕穆德来到了金字塔脚下,他想考一考年仅14岁的小穆罕穆德.给你一条2米高的木杆,一把皮尺,一面平面镜.你能利用所学知识来测出塔高吗?2米木杆皮尺平面镜古代一位数学家想出了一种测量金字塔高度的方法:如图所示,为了测量金字塔的高度DE,先竖一根已知长度的木棒BC, 比较棒子的影长FC与金字塔的影长AE,即可近似算出金字塔的高度. 如果BC=2,FC=4,AE=274,求金字塔的高度DE.AF解 由于太阳光是平行光线,因此
∠DAE=∠BFC.
又因为 ∠DEF=∠BCF=90°.
所以 △ADE∽△FBC
DE∶BC=AE∶FC,
DE= (米)
答:该金字塔高为137米.ACBDE┐┐例2.
小丽用下面的方法来测量学校教学大楼AB的高度,如图,在水平面上放一面镜子,镜子与教学大楼的距离EA=21米,当她与镜子的距离CE=2.5米时,她刚好能从镜子中看到教学大楼的顶端B,已知她的眼睛距地面高度DC=1.6米,请你帮助小计算出教学大楼AB的高度是多少米? 探索:如图,有一边长为5cm的正方形ABCD和等腰△PQR,PQ=RP,PE=3cm,QR=8cm,点B,C,Q,R共线.当C与Q重合时, △PQR以1cm/s 的速度沿着直线l按箭头的方向匀速运动, t秒后正方形ABCD与△PQR重合部分的面积为Scm2 ABCDl(1)当t=3秒时,求S的值. G(2) t=5秒呢?
小小科学家:1.如图,铁道口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高 m? oBDCA┏┛(第1题)1m16m0.5m8给我一个支点我可以撬起整个地球!---阿基米德2. 小明在打网球时,使球恰好能打过网,而且落在离网5米的位置上,求球拍击球的高度h.
(设网球是直线运动)
(第2题)ADBCE┏┏小小科学家:oBDCA┏┛(第1题)1m16m0.5m(第2题)ADBCE┏┏问题二如图18.3.13,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB. 图18.3.13解 因为∠ADB=∠EDC,
∠ABC=∠ECD=90°
所以 △ABD∽△ECD,
那么
解得AB=
=
=100(米).
答: 两岸间的大致距离为100米. 小小设计家: 如图所示,钱塘江的一侧有A,B两个工厂.现要在江边建造一个水厂C,把水送到这两个工厂,要使供水管路线最短.这样可以节省成本.ABED1.请你设计一下水厂应该建造在哪里? 2.若AE=0.5千米,BD=1.5千米,且DE=3 千米.求水厂C距离D处有多远? ..FC小小实践家:ABDCO有一如图所示的容器,现给出下列工具请测量出CD的长度生活实践 1、如图,是一池塘的平面图,请你利用相似三角形的知识,设计出一种测量A、B两点间距离的方案,并对这种方案作出简要的说明。解:如图在池塘外选一点P,连AP并延长,连BP并延长使 或其他值), 则△ABP∽△CDP得 ,量出CD的长就可算出 AB的长。
小小演说家: 通过本堂课的学习和探索,你学会了什么?
2. 谈一谈!你对这堂课的感受?
1. 在实际生活中, 我们面对不能直接测量物体的高度和宽度时. 可以把它们转化为数学问题,建立相似三角形模型,再利用对应边成比例来达到求解的目的!
2. 能掌握并应用一些简单的相似三角形模型. ⑴⑶⑷ 作 业1. 在同一时刻物体的高度与它的影长成正比例.在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为60米,那么高楼的高度是多少米?ABCED2. 小明要测量一座古塔的高度,从距他2米的一小块积水处C看到塔顶的倒影,已知小明的眼部离地面的高度DE是1.5米,塔底中心B到积水处C的距离是40米.求塔高? 小小实践家:液面BCA木棒 如何来测量液面的高度呢?提供工具:
木棒(足够长),刻度尺D小小实践家:液面BCA木棒ABCDEGD小小实践家:液面BCA木棒ABCDEGBCAED
两三角形相似(3)三边对应成比例的两三角形相似复习相似三角形的性质6、相似三角形周长的比等于相似比5、相似三角形对应角平分线的比等于相似比复习4、相似三角形对应中线的比等于相似比7、相似三角形面积的比等于3、相似三角形对应高的比等于相似比1、相似三角形对应角相等2、相似三角形对应边成比例相似比的平方1. 如图(1),在△ABC中,DE∥AC,BD=10,DA=15,BE=8,则EC=
.课前训练:BDECA2.如图(2),已知 ∠ 1 = ∠ 2,若再增加一个条件就能使结论“△ADE∽△ABC”成立,则这条件可以是(1)ADBE(2)C12解:设楼的高度为x米,由题意得:
例1.在同一时刻物体的高度与它的影长成正比例.在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为60米,那么高楼的高度是多少米? 解得x=36(米)答:楼的高度是36米。 测量学校旗杆的高度。
古埃及所有金字塔中最大的一座是第四王朝法老胡夫王的金字塔。这座大金字塔原高146.59m,经过几千年的风吹雨打,顶端被风化吹蚀了近10m。在巴黎埃菲尔铁塔完成之前,它一直是世界上最高的建筑物。这座金字塔的底面呈正方形,边长大约230m。但由于经过几千年的风吹雨打,顶端被风化吹蚀.所以高度有所降低 。 走近金字塔小小考古家: 埃及著名的考古专家穆罕穆德决定重新测量胡夫金字塔的高度.在一个烈日高照的上午.他和儿子小穆罕穆德来到了金字塔脚下,他想考一考年仅14岁的小穆罕穆德.给你一条2米高的木杆,一把皮尺,一面平面镜.你能利用所学知识来测出塔高吗?2米木杆皮尺平面镜古代一位数学家想出了一种测量金字塔高度的方法:如图所示,为了测量金字塔的高度DE,先竖一根已知长度的木棒BC, 比较棒子的影长FC与金字塔的影长AE,即可近似算出金字塔的高度. 如果BC=2,FC=4,AE=274,求金字塔的高度DE.AF解 由于太阳光是平行光线,因此
∠DAE=∠BFC.
又因为 ∠DEF=∠BCF=90°.
所以 △ADE∽△FBC
DE∶BC=AE∶FC,
DE= (米)
答:该金字塔高为137米.ACBDE┐┐例2.
小丽用下面的方法来测量学校教学大楼AB的高度,如图,在水平面上放一面镜子,镜子与教学大楼的距离EA=21米,当她与镜子的距离CE=2.5米时,她刚好能从镜子中看到教学大楼的顶端B,已知她的眼睛距地面高度DC=1.6米,请你帮助小计算出教学大楼AB的高度是多少米? 探索:如图,有一边长为5cm的正方形ABCD和等腰△PQR,PQ=RP,PE=3cm,QR=8cm,点B,C,Q,R共线.当C与Q重合时, △PQR以1cm/s 的速度沿着直线l按箭头的方向匀速运动, t秒后正方形ABCD与△PQR重合部分的面积为Scm2 ABCDl(1)当t=3秒时,求S的值. G(2) t=5秒呢?
小小科学家:1.如图,铁道口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高 m? oBDCA┏┛(第1题)1m16m0.5m8给我一个支点我可以撬起整个地球!---阿基米德2. 小明在打网球时,使球恰好能打过网,而且落在离网5米的位置上,求球拍击球的高度h.
(设网球是直线运动)
(第2题)ADBCE┏┏小小科学家:oBDCA┏┛(第1题)1m16m0.5m(第2题)ADBCE┏┏问题二如图18.3.13,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB. 图18.3.13解 因为∠ADB=∠EDC,
∠ABC=∠ECD=90°
所以 △ABD∽△ECD,
那么
解得AB=
=
=100(米).
答: 两岸间的大致距离为100米. 小小设计家: 如图所示,钱塘江的一侧有A,B两个工厂.现要在江边建造一个水厂C,把水送到这两个工厂,要使供水管路线最短.这样可以节省成本.ABED1.请你设计一下水厂应该建造在哪里? 2.若AE=0.5千米,BD=1.5千米,且DE=3 千米.求水厂C距离D处有多远? ..FC小小实践家:ABDCO有一如图所示的容器,现给出下列工具请测量出CD的长度生活实践 1、如图,是一池塘的平面图,请你利用相似三角形的知识,设计出一种测量A、B两点间距离的方案,并对这种方案作出简要的说明。解:如图在池塘外选一点P,连AP并延长,连BP并延长使 或其他值), 则△ABP∽△CDP得 ,量出CD的长就可算出 AB的长。
小小演说家: 通过本堂课的学习和探索,你学会了什么?
2. 谈一谈!你对这堂课的感受?
1. 在实际生活中, 我们面对不能直接测量物体的高度和宽度时. 可以把它们转化为数学问题,建立相似三角形模型,再利用对应边成比例来达到求解的目的!
2. 能掌握并应用一些简单的相似三角形模型. ⑴⑶⑷ 作 业1. 在同一时刻物体的高度与它的影长成正比例.在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为60米,那么高楼的高度是多少米?ABCED2. 小明要测量一座古塔的高度,从距他2米的一小块积水处C看到塔顶的倒影,已知小明的眼部离地面的高度DE是1.5米,塔底中心B到积水处C的距离是40米.求塔高? 小小实践家:液面BCA木棒 如何来测量液面的高度呢?提供工具:
木棒(足够长),刻度尺D小小实践家:液面BCA木棒ABCDEGD小小实践家:液面BCA木棒ABCDEGBCAED
