2023年湖南省普通高中学业水平合格性考试数学试题(无答案)
文档属性
| 名称 | 2023年湖南省普通高中学业水平合格性考试数学试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 293.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-10 06:47:34 | ||
图片预览

文档简介
2023年湖南省普通高中学业水平合格性考试数学试题
一、单选题(共54分)
1.(本题3分)已知集合},,则( )
A. B.
C. D.
2.(本题3分)命题“,”的否定是
A., B.,
C., D.,
3.(本题3分) 2021年5月30日清晨5时01分,天舟二号货运飞船在成功发射约8小时后,与中国空间站天和核心舱完成自主快速交接.如果下次执行空间站的任务由3名航天员承担,需要在3名女性航天员和4名男性航天员中选择,则选出的3名航天员中既有男性航天员又有女性航天员的概率为( )
A. B. C. D.
4.(本题3分)函数的定义域为( )
A. B. C. D.
5.(本题3分)复数(i为虚数单位)的实部为( )
A.2 B. C. D.
6.(本题3分)函数的最小正周期是( )
A. B.π C.2π D.4π
7.(本题3分)下列四个函数中,在其定义域上既是奇函数又是增函数的是 ( )
A. B.y=tan x
C.y=lnx D.y=x|x|
8.(本题3分)已知直线l垂直于平面,另一直线m也垂直于平面,则直线l,m的位置关系是( )
A.平行 B.相交 C.垂直 D.异面
9.(本题3分)已知点是角终边上一点,则( )
A. B. C. D.
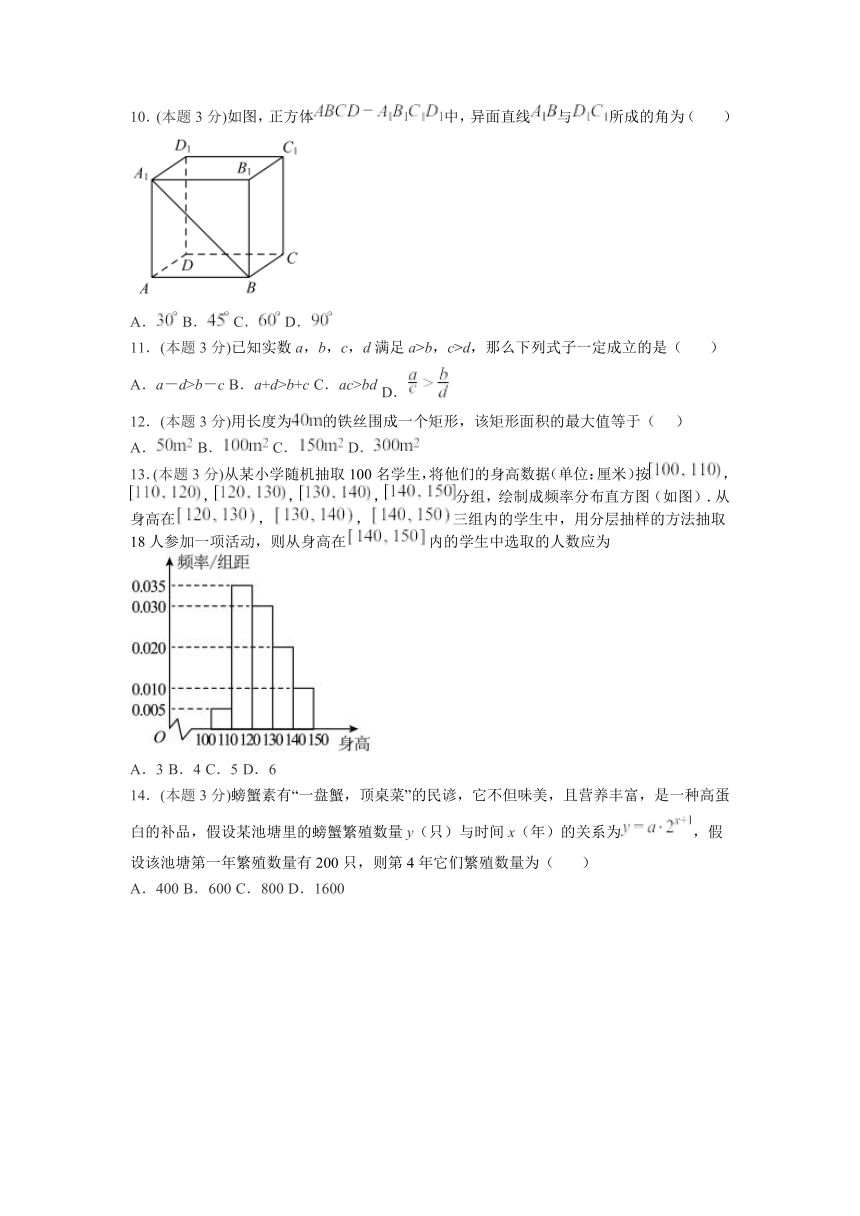
10.(本题3分)如图,正方体中,异面直线与所成的角为( )
A. B. C. D.
11.(本题3分)已知实数a,b,c,d满足a>b,c>d,那么下列式子一定成立的是( )
A.a-d>b-c B.a+d>b+c C.ac>bd D.
12.(本题3分)用长度为的铁丝围成一个矩形,该矩形面积的最大值等于( )
A. B. C. D.
13.(本题3分)从某小学随机抽取100名学生,将他们的身高数据(单位:厘米)按,,,,分组,绘制成频率分布直方图(如图).从身高在,,三组内的学生中,用分层抽样的方法抽取18人参加一项活动,则从身高在内的学生中选取的人数应为
A.3 B.4 C.5 D.6
14.(本题3分)螃蟹素有“一盘蟹,顶桌菜”的民谚,它不但味美,且营养丰富,是一种高蛋白的补品,假设某池塘里的螃蟹繁殖数量y(只)与时间x(年)的关系为,假设该池塘第一年繁殖数量有200只,则第4年它们繁殖数量为( )
A.400 B.600 C.800 D.1600
15.(本题3分)如图,点,,,均在正方形网格的格点上.若,则( )
A.1 B. C. D.2
16.(本题3分)已知在上单调递增,,那么是的
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
17.(本题3分)已知,则三者的大小关系是( )
A. B. C. D.
18.(本题3分)在中,,,为钝角,则的取值范围是( )
A. B. C. D.
第II卷(非选择题)
请点击修改第II卷的文字说明
二、填空题(共16分)
19.(本题4分)若指数函数的图象过点,则__________.
20.(本题4分)已知向量,,其中.若共线,则___.
21.(本题4分)2020年春季,受疫情的影响,学校推迟了开学时间上级部门倡导“停课不停学”,鼓励学生在家学习,复课后,某校为了解学生在家学习的周均时长(单位:小时),随机调查了部分学生,根据他们学习的周均时长,得到如图所示的频率分布直方图.则该校学生学习的周均时长的众数的估计值为___________.
22.(本题4分)请写出一个同时满足以下三个条件的函数:______.
(1)是偶函数;
(2)在上单调递增;
(3)的最小值是1.
三、解答题(共44分)
23.(本题6分)如图所示是某商家根据去年A,B两种产品的月销售额(单位:万元)作出的统计图(称为雷达图),根据图中信息,写出关于A,B两种产品销售额比较的两个统计结论.
24.(本题14分)如图,在四棱锥中,底面为平行四边形,,,,,且平面.
(1)证明:平面PBD;
(2)若Q为PC的中点,求三棱锥的体积.
25.(本题24分)已知在定义域内单调的函数满足恒成立.
(1)设,求实数的值;
(2)解不等式;
(3)设,若对于任意的恒成立,求实数的取值范围,并指出取等时的值.
一、单选题(共54分)
1.(本题3分)已知集合},,则( )
A. B.
C. D.
2.(本题3分)命题“,”的否定是
A., B.,
C., D.,
3.(本题3分) 2021年5月30日清晨5时01分,天舟二号货运飞船在成功发射约8小时后,与中国空间站天和核心舱完成自主快速交接.如果下次执行空间站的任务由3名航天员承担,需要在3名女性航天员和4名男性航天员中选择,则选出的3名航天员中既有男性航天员又有女性航天员的概率为( )
A. B. C. D.
4.(本题3分)函数的定义域为( )
A. B. C. D.
5.(本题3分)复数(i为虚数单位)的实部为( )
A.2 B. C. D.
6.(本题3分)函数的最小正周期是( )
A. B.π C.2π D.4π
7.(本题3分)下列四个函数中,在其定义域上既是奇函数又是增函数的是 ( )
A. B.y=tan x
C.y=lnx D.y=x|x|
8.(本题3分)已知直线l垂直于平面,另一直线m也垂直于平面,则直线l,m的位置关系是( )
A.平行 B.相交 C.垂直 D.异面
9.(本题3分)已知点是角终边上一点,则( )
A. B. C. D.
10.(本题3分)如图,正方体中,异面直线与所成的角为( )
A. B. C. D.
11.(本题3分)已知实数a,b,c,d满足a>b,c>d,那么下列式子一定成立的是( )
A.a-d>b-c B.a+d>b+c C.ac>bd D.
12.(本题3分)用长度为的铁丝围成一个矩形,该矩形面积的最大值等于( )
A. B. C. D.
13.(本题3分)从某小学随机抽取100名学生,将他们的身高数据(单位:厘米)按,,,,分组,绘制成频率分布直方图(如图).从身高在,,三组内的学生中,用分层抽样的方法抽取18人参加一项活动,则从身高在内的学生中选取的人数应为
A.3 B.4 C.5 D.6
14.(本题3分)螃蟹素有“一盘蟹,顶桌菜”的民谚,它不但味美,且营养丰富,是一种高蛋白的补品,假设某池塘里的螃蟹繁殖数量y(只)与时间x(年)的关系为,假设该池塘第一年繁殖数量有200只,则第4年它们繁殖数量为( )
A.400 B.600 C.800 D.1600
15.(本题3分)如图,点,,,均在正方形网格的格点上.若,则( )
A.1 B. C. D.2
16.(本题3分)已知在上单调递增,,那么是的
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
17.(本题3分)已知,则三者的大小关系是( )
A. B. C. D.
18.(本题3分)在中,,,为钝角,则的取值范围是( )
A. B. C. D.
第II卷(非选择题)
请点击修改第II卷的文字说明
二、填空题(共16分)
19.(本题4分)若指数函数的图象过点,则__________.
20.(本题4分)已知向量,,其中.若共线,则___.
21.(本题4分)2020年春季,受疫情的影响,学校推迟了开学时间上级部门倡导“停课不停学”,鼓励学生在家学习,复课后,某校为了解学生在家学习的周均时长(单位:小时),随机调查了部分学生,根据他们学习的周均时长,得到如图所示的频率分布直方图.则该校学生学习的周均时长的众数的估计值为___________.
22.(本题4分)请写出一个同时满足以下三个条件的函数:______.
(1)是偶函数;
(2)在上单调递增;
(3)的最小值是1.
三、解答题(共44分)
23.(本题6分)如图所示是某商家根据去年A,B两种产品的月销售额(单位:万元)作出的统计图(称为雷达图),根据图中信息,写出关于A,B两种产品销售额比较的两个统计结论.
24.(本题14分)如图,在四棱锥中,底面为平行四边形,,,,,且平面.
(1)证明:平面PBD;
(2)若Q为PC的中点,求三棱锥的体积.
25.(本题24分)已知在定义域内单调的函数满足恒成立.
(1)设,求实数的值;
(2)解不等式;
(3)设,若对于任意的恒成立,求实数的取值范围,并指出取等时的值.
同课章节目录
