24.3正多边形和圆(1)教案
文档属性
| 名称 | 24.3正多边形和圆(1)教案 |  | |
| 格式 | zip | ||
| 文件大小 | 165.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-23 17:24:47 | ||
图片预览


文档简介
教 案 首 页
教材版本 人教版 学段 初三 学科 数学
章节 第24章第3节 课题名 正多边形和圆 课时 第一课时
执教教师单位 南昌一中 教师姓名 郭君
教学目标 (1)知识目标:1、通过对正多边形与圆的关 ( http: / / www.21cnjy.com )系的探索,培养学生观察、猜想、推理、迁移及归纳能力,使学生初步掌握正多边形与圆的关系的定理。(2)能力目标:通过利用等分圆周的的方法 ( http: / / www.21cnjy.com ),探索正多边形与圆的关系,理解正多边形的中心,半径、中心角、边心距等有关概念,从而渗透归纳、分类讨论等数学思想。(3)情感目标:经历观察、发现、探索正多边形与圆的关系的数学活动中,感受到数学来源于生活,又服务于生活,体会到事物之间是互相联系,相互作用的。
教学重点 正多边形的概念与正多边形和圆的关系的定理。
教学难点 对正多边形与圆的关系的探索。
教具 多媒体幻灯片
时间安排 教学引入:1分钟探索新知:18分钟典例分析:15分钟巩固练习:10分钟小结:1分钟
课后小结 教学过程中,教学思想的渗透,抑制有助于逐渐培养学生数学素养。
正多边形和圆(1)
教学方法:采取引导发现法,创设合理的问题情境,激发学生思维的积极性,充分展现学生的主体作用.
组织教学:学生16人,要求积极思考、实验;
教学过程:
一、教学引入
二、探索新知
1、正多边形:各边相等,各角也相等
如果一个正多边形有n条边,那么这个正多边形叫做正n边形。
思考: 菱形是正多边形吗 矩形是正多边形呢 菱形, 矩形都不是正多边形
2、正多边形的性质
(1)、正多边形的各边相等
(2)、正多边形的各角相等
(3).正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都通过n边形的中心。
(4). 边数是偶数的正多边形,不但是轴对称图形, 还是中心对称图形,它的中心就是对称中心。
3、小试身手
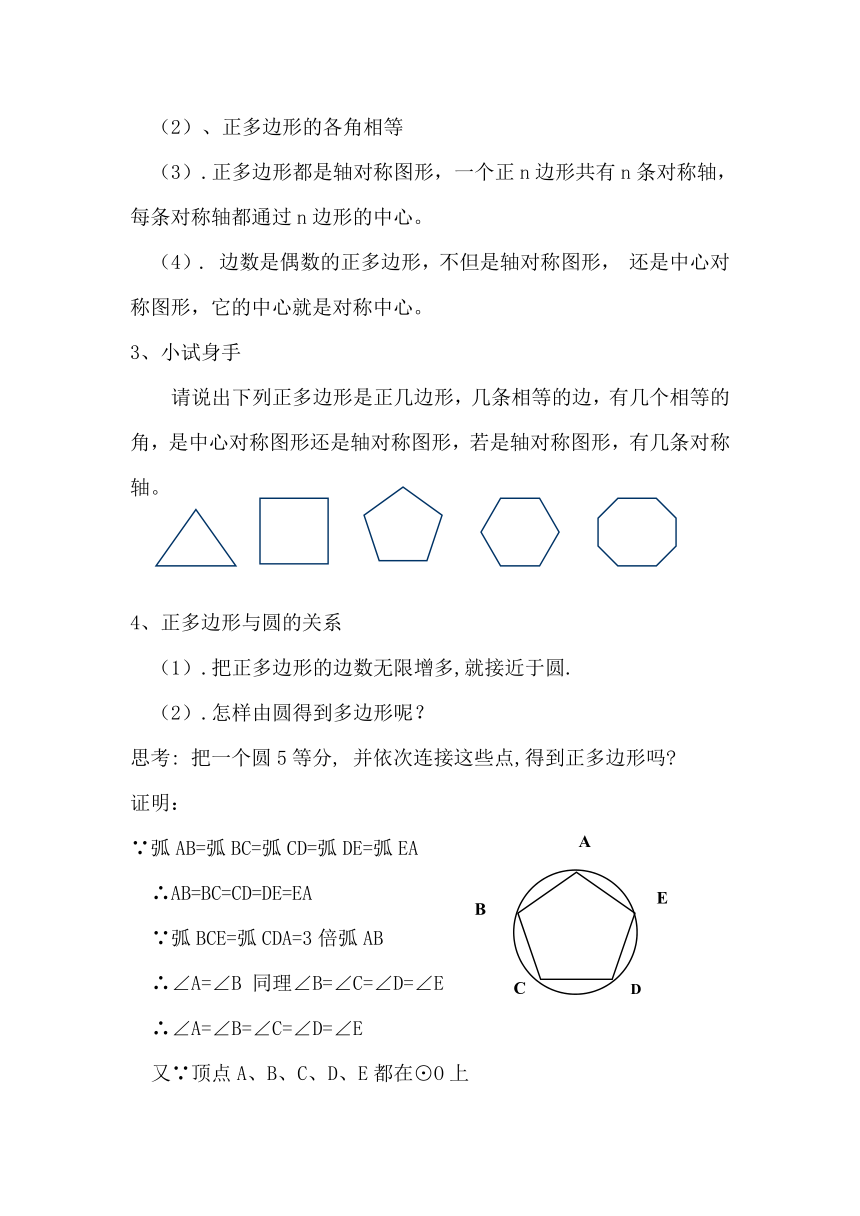
请说出下列正多边形是正几边形,几条相等的边,有几个相等的角,是中心对称图形还是轴对称图形,若是轴对称图形,有几条对称轴。
4、正多边形与圆的关系
(1).把正多边形的边数无限增多,就接近于圆.
(2).怎样由圆得到多边形呢?
思考: 把一个圆5等分, 并依次连接这些点,得到正多边形吗
证明:
∵弧AB=弧BC=弧CD=弧DE=弧EA
∴AB=BC=CD=DE=EA
∵弧BCE=弧CDA=3倍弧AB
∴∠A=∠B 同理∠B=∠C=∠D=∠E
∴∠A=∠B=∠C=∠D=∠E
又∵顶点A、B、C、D、E都在⊙O上
∴五边形ABCDE是⊙O的内接正五边形, ⊙O是五边形的外接圆。
5、正多边形有关的概念
把圆分成n(n≥3)等份:依次连结各分点所得的多边形是这个圆的内接正多边形.
正多边形的中心: 正多边形的外接圆的圆心.
正多边形的半径: 外接圆的半径
正多边形的中心角: 正多边形的每一条边所对的圆心角.
正多边形的边心距:中心到正多边形的一边的距离.
正多边形的内角:
正多边形的半径: 外接圆的半径
正多边形的中心角:
正多边形的边心距:
正多边形的面积:
三、典例分析
指出下图中有圆与圆的哪种位置关系?
例1、求证:正五边形的对角线相等。
已知:多边形ABCDE是正五边形。
求证:DB=CE
证明: 在△BCD和△CDE中
∵ BC=CD ∠BCD=∠CDE CD=DE
∴△BCD≌△CDE
∴BD=CE
同理可证其他对角线互相相等,
∴正五边形的对角线相等
例2、 有一个亭子它的地基是半径为4m的正六边形,求地基的周长和面积(结果保留小数点后一位).
四、巩固练习
1、口答
①矩形是正多边形吗?菱形呢?正方形呢?
②各边相等的圆内接多边形是正多边形吗?各角相等的圆内接多边形呢?如果不是,说明为什么;如果不是,举出反例。
2、计算
①正八边形的中心角是_____度;它的外角是___度。
②圆内接正方形的半径与边长的比值是________。
③已知圆内接正方形的边长为2,则该圆 的内接正六边形边长为__________。
④圆内接正六边形的边长是8 cm,那么该正六边形的半径为_______;边心距为________。
3、证明题。
求证:顺次连结正六边形各边中点所得的多边形是正六边形。
五、小 结
1、怎样的多边形是正多边形?
2、怎样判定一个多边形是正多边形?
3、利用多边形的一些性质进行有关计算。
六、作 业
1、课本第107页第1、2题2、课本第108页第5、6题
七、板书设计
A
C
D
E
B
E
F
C
D
.
中心角
半径R
A
B
O
边心距r
E
F
C
D
中心角
半径R
A
B
.
O
边心距r
A
B
C
D
E
解:
F
A
D
E
.
B
C
r
R
P
.
O
正多边形和圆
正多边形的性质
学生板演
正多边形的基本概念
例题
正多边形的定义
教材版本 人教版 学段 初三 学科 数学
章节 第24章第3节 课题名 正多边形和圆 课时 第一课时
执教教师单位 南昌一中 教师姓名 郭君
教学目标 (1)知识目标:1、通过对正多边形与圆的关 ( http: / / www.21cnjy.com )系的探索,培养学生观察、猜想、推理、迁移及归纳能力,使学生初步掌握正多边形与圆的关系的定理。(2)能力目标:通过利用等分圆周的的方法 ( http: / / www.21cnjy.com ),探索正多边形与圆的关系,理解正多边形的中心,半径、中心角、边心距等有关概念,从而渗透归纳、分类讨论等数学思想。(3)情感目标:经历观察、发现、探索正多边形与圆的关系的数学活动中,感受到数学来源于生活,又服务于生活,体会到事物之间是互相联系,相互作用的。
教学重点 正多边形的概念与正多边形和圆的关系的定理。
教学难点 对正多边形与圆的关系的探索。
教具 多媒体幻灯片
时间安排 教学引入:1分钟探索新知:18分钟典例分析:15分钟巩固练习:10分钟小结:1分钟
课后小结 教学过程中,教学思想的渗透,抑制有助于逐渐培养学生数学素养。
正多边形和圆(1)
教学方法:采取引导发现法,创设合理的问题情境,激发学生思维的积极性,充分展现学生的主体作用.
组织教学:学生16人,要求积极思考、实验;
教学过程:
一、教学引入
二、探索新知
1、正多边形:各边相等,各角也相等
如果一个正多边形有n条边,那么这个正多边形叫做正n边形。
思考: 菱形是正多边形吗 矩形是正多边形呢 菱形, 矩形都不是正多边形
2、正多边形的性质
(1)、正多边形的各边相等
(2)、正多边形的各角相等
(3).正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都通过n边形的中心。
(4). 边数是偶数的正多边形,不但是轴对称图形, 还是中心对称图形,它的中心就是对称中心。
3、小试身手
请说出下列正多边形是正几边形,几条相等的边,有几个相等的角,是中心对称图形还是轴对称图形,若是轴对称图形,有几条对称轴。
4、正多边形与圆的关系
(1).把正多边形的边数无限增多,就接近于圆.
(2).怎样由圆得到多边形呢?
思考: 把一个圆5等分, 并依次连接这些点,得到正多边形吗
证明:
∵弧AB=弧BC=弧CD=弧DE=弧EA
∴AB=BC=CD=DE=EA
∵弧BCE=弧CDA=3倍弧AB
∴∠A=∠B 同理∠B=∠C=∠D=∠E
∴∠A=∠B=∠C=∠D=∠E
又∵顶点A、B、C、D、E都在⊙O上
∴五边形ABCDE是⊙O的内接正五边形, ⊙O是五边形的外接圆。
5、正多边形有关的概念
把圆分成n(n≥3)等份:依次连结各分点所得的多边形是这个圆的内接正多边形.
正多边形的中心: 正多边形的外接圆的圆心.
正多边形的半径: 外接圆的半径
正多边形的中心角: 正多边形的每一条边所对的圆心角.
正多边形的边心距:中心到正多边形的一边的距离.
正多边形的内角:
正多边形的半径: 外接圆的半径
正多边形的中心角:
正多边形的边心距:
正多边形的面积:
三、典例分析
指出下图中有圆与圆的哪种位置关系?
例1、求证:正五边形的对角线相等。
已知:多边形ABCDE是正五边形。
求证:DB=CE
证明: 在△BCD和△CDE中
∵ BC=CD ∠BCD=∠CDE CD=DE
∴△BCD≌△CDE
∴BD=CE
同理可证其他对角线互相相等,
∴正五边形的对角线相等
例2、 有一个亭子它的地基是半径为4m的正六边形,求地基的周长和面积(结果保留小数点后一位).
四、巩固练习
1、口答
①矩形是正多边形吗?菱形呢?正方形呢?
②各边相等的圆内接多边形是正多边形吗?各角相等的圆内接多边形呢?如果不是,说明为什么;如果不是,举出反例。
2、计算
①正八边形的中心角是_____度;它的外角是___度。
②圆内接正方形的半径与边长的比值是________。
③已知圆内接正方形的边长为2,则该圆 的内接正六边形边长为__________。
④圆内接正六边形的边长是8 cm,那么该正六边形的半径为_______;边心距为________。
3、证明题。
求证:顺次连结正六边形各边中点所得的多边形是正六边形。
五、小 结
1、怎样的多边形是正多边形?
2、怎样判定一个多边形是正多边形?
3、利用多边形的一些性质进行有关计算。
六、作 业
1、课本第107页第1、2题2、课本第108页第5、6题
七、板书设计
A
C
D
E
B
E
F
C
D
.
中心角
半径R
A
B
O
边心距r
E
F
C
D
中心角
半径R
A
B
.
O
边心距r
A
B
C
D
E
解:
F
A
D
E
.
B
C
r
R
P
.
O
正多边形和圆
正多边形的性质
学生板演
正多边形的基本概念
例题
正多边形的定义
同课章节目录
