1.3 正方形的性质与判定(第三课时) 课件(19张PPT)
文档属性
| 名称 | 1.3 正方形的性质与判定(第三课时) 课件(19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-10 16:03:43 | ||
图片预览


文档简介
1.3 正方形的性质与判定
第一章 特殊平行四边形
第三课时 中点四边形
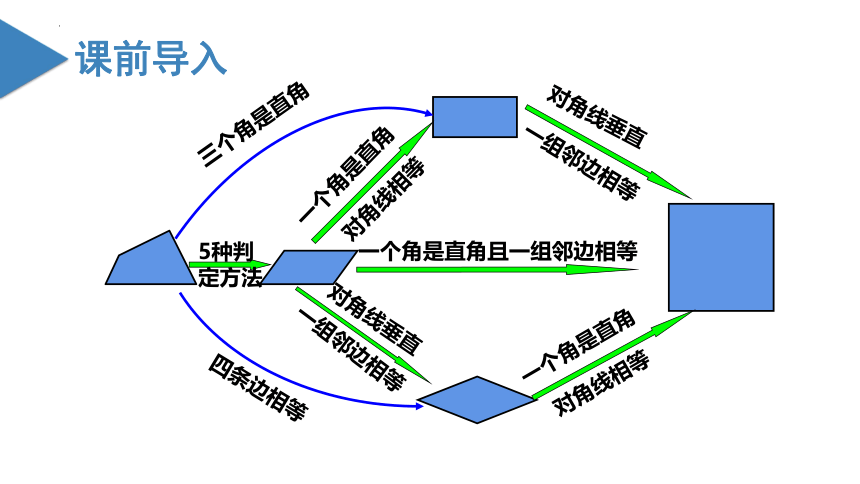
5种判定方法
三个角是直角
四条边相等
一个角是直角
对角线相等
一组邻边相等
对角线垂直
一组邻边相等
对角线垂直
一个角是直角
对角线相等
一个角是直角且一组邻边相等
中点四边形的定义:依次连接任意一个四边形各边中点所得的四边形叫做中点四边形。
【猜想】中点四边形有哪些性质?并尝试证明?
已知点E、F、G、H分别为四边形ABCD四条边AB、BC、CD、AD的中点,则
猜想1:四边形EFGH是平行四边形
猜想2:CEFGH =AC+BD
猜想3:sEFGH =12sABCD
?
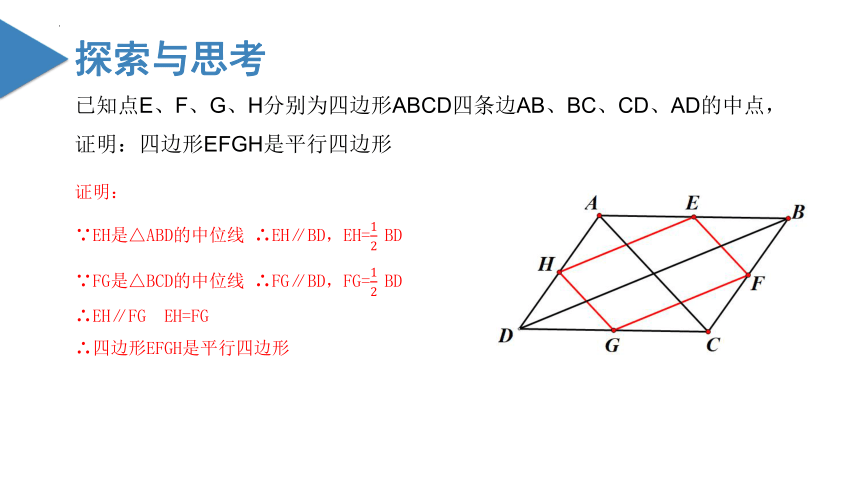
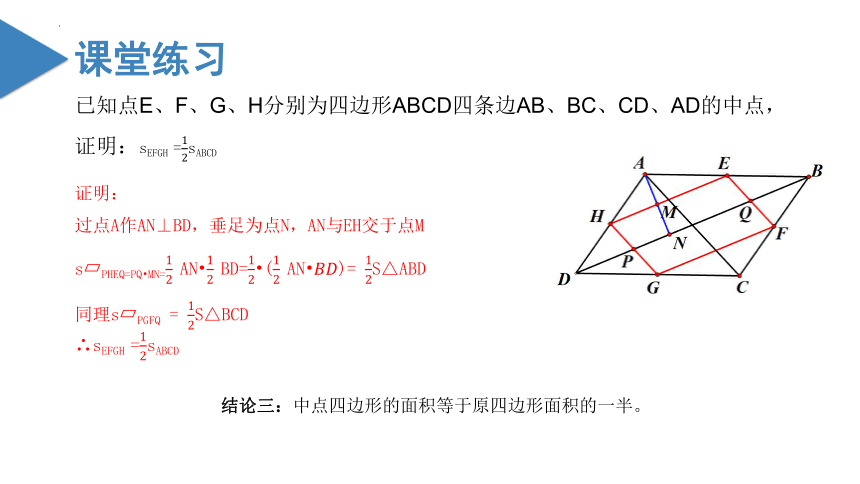
已知点E、F、G、H分别为四边形ABCD四条边AB、BC、CD、AD的中点,
证明:四边形EFGH是平行四边形
证明:
∵EH是△ABD的中位线 ∴EH∥BD,EH=12?BD
∵FG是△BCD的中位线 ∴FG∥BD,FG=12?BD
∴EH∥FG EH=FG
∴四边形EFGH是平行四边形
?
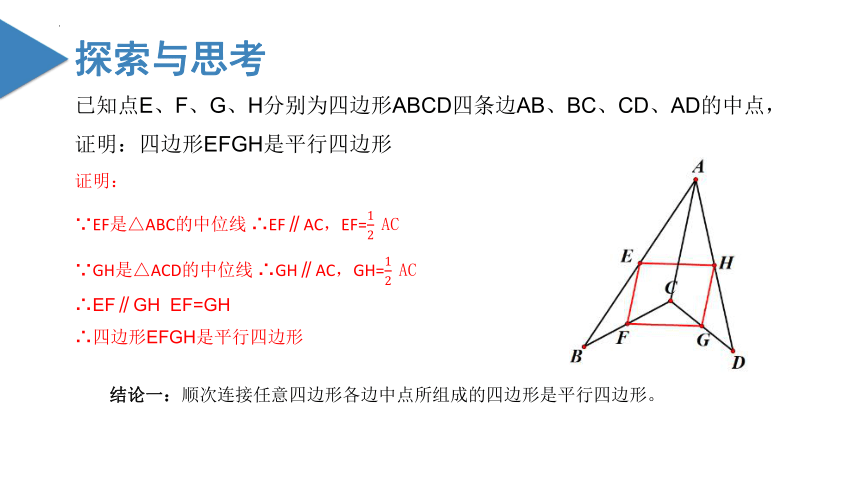
已知点E、F、G、H分别为四边形ABCD四条边AB、BC、CD、AD的中点,
证明:四边形EFGH是平行四边形
证明:
∵EF是△ABC的中位线 ∴EF∥AC,EF=12?AC
∵GH是△ACD的中位线 ∴GH∥AC,GH=12?AC
∴EF∥GH EF=GH
∴四边形EFGH是平行四边形
?
结论一:顺次连接任意四边形各边中点所组成的四边形是平行四边形。
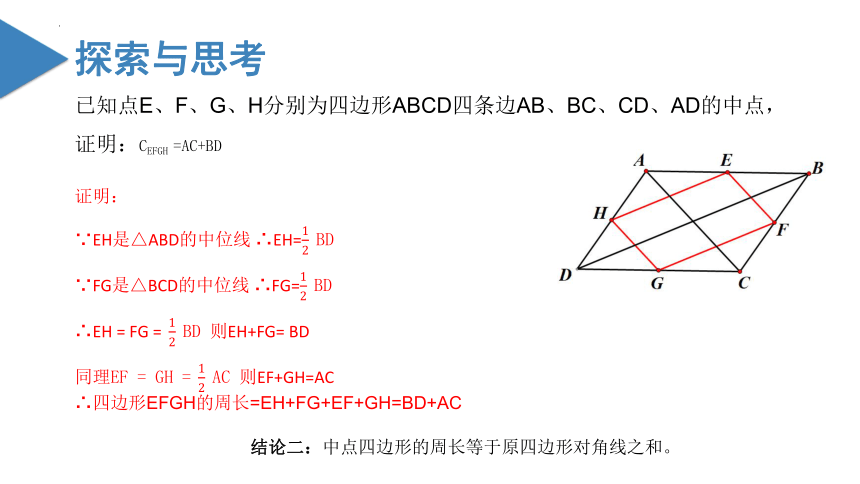
已知点E、F、G、H分别为四边形ABCD四条边AB、BC、CD、AD的中点,
证明:CEFGH =AC+BD
证明:
∵EH是△ABD的中位线 ∴EH=12?BD
∵FG是△BCD的中位线 ∴FG=12?BD
∴EH = FG =?12?BD 则EH+FG= BD
同理EF = GH =?12?AC 则EF+GH=AC
∴四边形EFGH的周长=EH+FG+EF+GH=BD+AC
?
结论二:中点四边形的周长等于原四边形对角线之和。
已知点E、F、G、H分别为四边形ABCD四条边AB、BC、CD、AD的中点,
证明:sEFGH =12sABCD
?
证明:
过点A作AN⊥BD,垂足为点N,AN与EH交于点M
s?PHEQ=PQ?MN=12?AN?12?BD=12?(12?AN?????????)= 12S△ABD
同理s?PGFQ = 12S△BCD
∴sEFGH =12sABCD
?
结论三:中点四边形的面积等于原四边形面积的一半。
【探究1】以菱形各边的中点为顶点组成的四边形会是什么形状?
已知:如图,点 E,F,G,H 分别是菱形 ABCD 各边的中点.
求证:四边形EFGH为矩形.
证明:连接 AC,BD,
∵ E,F分别是 AB 和 BC 边中点,
∴ EF∥AC,同理可证 HG∥AC,EH∥BD,FG∥BD.
∴ EF∥HG,EH∥FG,
∴ 四边形EFGH为平行四边形
又∵AC⊥BD, EH∥BD
∴ AC⊥EH 而HG∥AC
∴ HG⊥EH 则∠EHG=90°
∴四边形 EFGH 是矩形(矩形的定义)
已知:如图,点E、F、G、H是任意四边形ABCD的中点,AC⊥DB,垂足为点O.
求证:四边形EFGH为矩形.
证明:
根据已知条件可知四边形EFGH为平行四边形
∵AC⊥DB ∠DOC=90°
∵E,F,G,H分别是AB,BC,CD,DA的中点,
∴HE∥BD∥GF,HG∥AC∥EF
∴∠EHG=∠HGF=∠GFE=∠FEH=90?°
∴四边形EFGH是矩形。
结论四:顺次连接对角线互相垂直的四边形各边中点所组成的四边形是矩形。
【探究2】以矩形各边的中点为顶点组成的四边形会是什么形状?
已知:如图,点E,F,G,H分别是矩形 ABCD 各边的中点.
求证:四边形EFGH为菱形.
证明:连接AC、BD
由探究1可知,四边形 EFGH 为平行四边形.
又∵四边形ABCD是矩形
∴AC=BD(矩形的对角线相等),
∴EF=EH
∴四边形EFGH是菱形(菱形的定义)
已知:如图,点E、F、G、H是任意四边形ABCD的中点,AC=DB,垂足为点O.
求证:四边形EFGH为矩形.
证明:
∵EF是?ABC的中位线 ∴EF=12????????
∵HG是?ADC的中位线 ∴HG=12????????
∴EF=HG=12???????? 同理EH=FG=12????????
∵AC=DB ∴EF=HG=EH=FG
∴四边形EFGH是菱形
?
结论五:顺次连接对角线相等的四边形各边中点所组成的四边形是菱形。
【思路】利用三角形的中位线及正方形的性质证出EH=GH=FG=EF,从而得到四边形EFGH是菱形,再根据EH ⊥GH得出EFGH是正方形。
已知:如图,点 E,F,G,H 分别是正方形 ABCD 各边的中点.
求证:四边形EFGH为正方形.
已知:点E、F、G、H是任意四边形ABCD的中点,AC⊥DB,AC=DB垂足为点O.
求证:四边形EFGH为正方形.
证明:
已知四边形EFGH是菱形(参考上述证明过程)
∵AC⊥DB,AC∥EH
∴EH⊥DB 而EF∥BD
∴EF⊥EH
∴四边形EFGH是正方形
结论六:顺次连接对角线互相垂直且相等的四边形各边中点所组成的四边形是正方形。
中点四边形的性质:
已知点E、F、G、H分别为四边形ABCD四条边AB、BC、CD、AD的中点,则
①四边形EFGH是平行四边形 ②CEFGH =AC+BD ③sEFGH =12sABCD
结论一:顺次连接任意四边形各边中点所组成的四边形是平行四边形。
结论二:中点四边形的周长等于原四边形对角线之和。
结论三:中点四边形的面积等于原四边形面积的一半。
结论四:顺次连接对角线互相垂直的四边形各边中点所组成的四边形是矩形。
结论五:顺次连接对角线相等的四边形各边中点所组成的四边形是菱形。
结论六:顺次连接对角线互相垂直且相等的四边形各边中点所组成的四边形是正方形。
速记口诀:矩中菱,菱中矩,正中正。
?
1.顺次连接菱形中点得到的四边形具备,而平行四边形不具备的性质是(????)
A.对角线相互平分 B.对角线相等
C.两组对角分别相等 D.两组对边分别平行
【详解】解:顺次连接菱形中点得到的四边形是矩形,矩形具有而平行四边形不具有的性质为:对角线相等.故选:B.
2.如图,在四边形ABCD中,点E,F,G,H分别是AB,CD,AC,BD的中点,添加下列条件,可以判定四边形EHFG为菱形的是(????)
A.AC=BD B.AB∥CD C.AD=BC D.AC⊥BD
?
【详解】解:添加????????=????????,可以判定四边形????????????????为菱形,理由:
∵点E,F,G,H分别是????????,????????,????????,????????的中点,
∴????????∥????????,????????=12????????,????????∥????????,????????=12????????,????????=12????????,
∴????????=????????=12????????,????????∥????????,
∴四边形????????????????为平行四边形,
∴当????????=????????时,????????=????????,
∴四边形????????????????为菱形.
故选:C.
?
3.如图,四边形ABCD四边的中点分别为E,F,G,H,对角线AC与BD相交于点O,若四边形EFGH的周长是3,则AC+BD的长为(????)
A.3 B.6 C.9 D.12
【详解】解:如图,
∵E、F、G、H分别是线段AB、BC、CD、AD的中点,
∴EH、FG分别是△ABD、△BCD的中位线,EF、HG分别是△ACD、△ABC的中位线,
根据三角形的中位线的性质知:
EF∥AC,GH∥AC且EF=GH=12AC,EH=FG=12BD,
∴四边形EFGH是平行四边形,
∵四边形EFGH的周长是3,即EF+GH+EH+FG=3,
∴AC+BD=3,
故选:A.
?
4. 如图,在任意四边形ABCD中,M,N,P,Q分别是AB,BC,CD,DA上的点,对于四边形MNPQ的形状,以下结论中,错误的是( )
A.当M,N,P,Q是各边中点,四边MNPQ一定为平行四边形
B.当M,N,P,Q是各边中点,且∠????????????=90?时,四边形MNPQ为正方形
C.当M,N、P,Q是各边中点,且????????=????????时,四边形MNPQ为菱形
D.当M,N、P、Q是各边中点,且????????⊥????????时,四边形MNPQ为矩形
?
【详解】解:连接AC、BD交于点O,
∵M,N,P,Q是各边中点,∴????????∥????????,????????=12????????,????????∥????????,????????=12????????,
∴????????∥????????,????????=????????,∴四边MNPQ一定为平行四边形,A说法正确,不符合题意;
∠????????????=90?时,四边形MNPQ不一定为正方形,B说法错误,符合题意;
????????=????????时,????????=????????,∴四边形MNPQ为菱形,C说法正确,不符合题意;
????????⊥????????时,∠????????????=90?,
∴四边形MNPQ为矩形,D说法正确,不符合题意.
故选B.
?
5. 如图,点E、F、G、H分别是四边形ABCD的边AB、BC、CD、DA的中点.则下列说法:
①若AC=BD,则四边形EFGH为矩形;②若????????⊥????????,则四边形EFGH为菱形;
③若AC与BD互相垂直且相等,则四边形EFGH是正方形;④若四边形EFGH是平行四边形,则AC与BD互相平分.其中正确的个数是(????)
A.1 B.2 C.3 D.4
?
【详解】解:∵点E、F、G、H分别是四边形ABCD的边AB、BC、CD、DA的中点,
∴EH是△ABD的中位线,∴EH=12BD,EH∥BD,
同理GF=12BD,EF=12AC,GH=12AC,EF∥AC
∴EH=GF,GH=EF,∴四边形EFGH是平行四边形,
①若AC=BD,则EH=GF=GH=EF,则四边形EFGH是菱形,故①错误;
②若AC⊥BD,则EF⊥EH,∴平行四边形EFGH是矩形,故②错误;
③若AC与BD互相垂直且相等,结合①②的判断可知四边形EFGH是正方形,故③正确;
④若四边形EFGH是平行四边形,并不能推出AC与BD互相平分,故④错误,故选A.
第一章 特殊平行四边形
第三课时 中点四边形
5种判定方法
三个角是直角
四条边相等
一个角是直角
对角线相等
一组邻边相等
对角线垂直
一组邻边相等
对角线垂直
一个角是直角
对角线相等
一个角是直角且一组邻边相等
中点四边形的定义:依次连接任意一个四边形各边中点所得的四边形叫做中点四边形。
【猜想】中点四边形有哪些性质?并尝试证明?
已知点E、F、G、H分别为四边形ABCD四条边AB、BC、CD、AD的中点,则
猜想1:四边形EFGH是平行四边形
猜想2:CEFGH =AC+BD
猜想3:sEFGH =12sABCD
?
已知点E、F、G、H分别为四边形ABCD四条边AB、BC、CD、AD的中点,
证明:四边形EFGH是平行四边形
证明:
∵EH是△ABD的中位线 ∴EH∥BD,EH=12?BD
∵FG是△BCD的中位线 ∴FG∥BD,FG=12?BD
∴EH∥FG EH=FG
∴四边形EFGH是平行四边形
?
已知点E、F、G、H分别为四边形ABCD四条边AB、BC、CD、AD的中点,
证明:四边形EFGH是平行四边形
证明:
∵EF是△ABC的中位线 ∴EF∥AC,EF=12?AC
∵GH是△ACD的中位线 ∴GH∥AC,GH=12?AC
∴EF∥GH EF=GH
∴四边形EFGH是平行四边形
?
结论一:顺次连接任意四边形各边中点所组成的四边形是平行四边形。
已知点E、F、G、H分别为四边形ABCD四条边AB、BC、CD、AD的中点,
证明:CEFGH =AC+BD
证明:
∵EH是△ABD的中位线 ∴EH=12?BD
∵FG是△BCD的中位线 ∴FG=12?BD
∴EH = FG =?12?BD 则EH+FG= BD
同理EF = GH =?12?AC 则EF+GH=AC
∴四边形EFGH的周长=EH+FG+EF+GH=BD+AC
?
结论二:中点四边形的周长等于原四边形对角线之和。
已知点E、F、G、H分别为四边形ABCD四条边AB、BC、CD、AD的中点,
证明:sEFGH =12sABCD
?
证明:
过点A作AN⊥BD,垂足为点N,AN与EH交于点M
s?PHEQ=PQ?MN=12?AN?12?BD=12?(12?AN?????????)= 12S△ABD
同理s?PGFQ = 12S△BCD
∴sEFGH =12sABCD
?
结论三:中点四边形的面积等于原四边形面积的一半。
【探究1】以菱形各边的中点为顶点组成的四边形会是什么形状?
已知:如图,点 E,F,G,H 分别是菱形 ABCD 各边的中点.
求证:四边形EFGH为矩形.
证明:连接 AC,BD,
∵ E,F分别是 AB 和 BC 边中点,
∴ EF∥AC,同理可证 HG∥AC,EH∥BD,FG∥BD.
∴ EF∥HG,EH∥FG,
∴ 四边形EFGH为平行四边形
又∵AC⊥BD, EH∥BD
∴ AC⊥EH 而HG∥AC
∴ HG⊥EH 则∠EHG=90°
∴四边形 EFGH 是矩形(矩形的定义)
已知:如图,点E、F、G、H是任意四边形ABCD的中点,AC⊥DB,垂足为点O.
求证:四边形EFGH为矩形.
证明:
根据已知条件可知四边形EFGH为平行四边形
∵AC⊥DB ∠DOC=90°
∵E,F,G,H分别是AB,BC,CD,DA的中点,
∴HE∥BD∥GF,HG∥AC∥EF
∴∠EHG=∠HGF=∠GFE=∠FEH=90?°
∴四边形EFGH是矩形。
结论四:顺次连接对角线互相垂直的四边形各边中点所组成的四边形是矩形。
【探究2】以矩形各边的中点为顶点组成的四边形会是什么形状?
已知:如图,点E,F,G,H分别是矩形 ABCD 各边的中点.
求证:四边形EFGH为菱形.
证明:连接AC、BD
由探究1可知,四边形 EFGH 为平行四边形.
又∵四边形ABCD是矩形
∴AC=BD(矩形的对角线相等),
∴EF=EH
∴四边形EFGH是菱形(菱形的定义)
已知:如图,点E、F、G、H是任意四边形ABCD的中点,AC=DB,垂足为点O.
求证:四边形EFGH为矩形.
证明:
∵EF是?ABC的中位线 ∴EF=12????????
∵HG是?ADC的中位线 ∴HG=12????????
∴EF=HG=12???????? 同理EH=FG=12????????
∵AC=DB ∴EF=HG=EH=FG
∴四边形EFGH是菱形
?
结论五:顺次连接对角线相等的四边形各边中点所组成的四边形是菱形。
【思路】利用三角形的中位线及正方形的性质证出EH=GH=FG=EF,从而得到四边形EFGH是菱形,再根据EH ⊥GH得出EFGH是正方形。
已知:如图,点 E,F,G,H 分别是正方形 ABCD 各边的中点.
求证:四边形EFGH为正方形.
已知:点E、F、G、H是任意四边形ABCD的中点,AC⊥DB,AC=DB垂足为点O.
求证:四边形EFGH为正方形.
证明:
已知四边形EFGH是菱形(参考上述证明过程)
∵AC⊥DB,AC∥EH
∴EH⊥DB 而EF∥BD
∴EF⊥EH
∴四边形EFGH是正方形
结论六:顺次连接对角线互相垂直且相等的四边形各边中点所组成的四边形是正方形。
中点四边形的性质:
已知点E、F、G、H分别为四边形ABCD四条边AB、BC、CD、AD的中点,则
①四边形EFGH是平行四边形 ②CEFGH =AC+BD ③sEFGH =12sABCD
结论一:顺次连接任意四边形各边中点所组成的四边形是平行四边形。
结论二:中点四边形的周长等于原四边形对角线之和。
结论三:中点四边形的面积等于原四边形面积的一半。
结论四:顺次连接对角线互相垂直的四边形各边中点所组成的四边形是矩形。
结论五:顺次连接对角线相等的四边形各边中点所组成的四边形是菱形。
结论六:顺次连接对角线互相垂直且相等的四边形各边中点所组成的四边形是正方形。
速记口诀:矩中菱,菱中矩,正中正。
?
1.顺次连接菱形中点得到的四边形具备,而平行四边形不具备的性质是(????)
A.对角线相互平分 B.对角线相等
C.两组对角分别相等 D.两组对边分别平行
【详解】解:顺次连接菱形中点得到的四边形是矩形,矩形具有而平行四边形不具有的性质为:对角线相等.故选:B.
2.如图,在四边形ABCD中,点E,F,G,H分别是AB,CD,AC,BD的中点,添加下列条件,可以判定四边形EHFG为菱形的是(????)
A.AC=BD B.AB∥CD C.AD=BC D.AC⊥BD
?
【详解】解:添加????????=????????,可以判定四边形????????????????为菱形,理由:
∵点E,F,G,H分别是????????,????????,????????,????????的中点,
∴????????∥????????,????????=12????????,????????∥????????,????????=12????????,????????=12????????,
∴????????=????????=12????????,????????∥????????,
∴四边形????????????????为平行四边形,
∴当????????=????????时,????????=????????,
∴四边形????????????????为菱形.
故选:C.
?
3.如图,四边形ABCD四边的中点分别为E,F,G,H,对角线AC与BD相交于点O,若四边形EFGH的周长是3,则AC+BD的长为(????)
A.3 B.6 C.9 D.12
【详解】解:如图,
∵E、F、G、H分别是线段AB、BC、CD、AD的中点,
∴EH、FG分别是△ABD、△BCD的中位线,EF、HG分别是△ACD、△ABC的中位线,
根据三角形的中位线的性质知:
EF∥AC,GH∥AC且EF=GH=12AC,EH=FG=12BD,
∴四边形EFGH是平行四边形,
∵四边形EFGH的周长是3,即EF+GH+EH+FG=3,
∴AC+BD=3,
故选:A.
?
4. 如图,在任意四边形ABCD中,M,N,P,Q分别是AB,BC,CD,DA上的点,对于四边形MNPQ的形状,以下结论中,错误的是( )
A.当M,N,P,Q是各边中点,四边MNPQ一定为平行四边形
B.当M,N,P,Q是各边中点,且∠????????????=90?时,四边形MNPQ为正方形
C.当M,N、P,Q是各边中点,且????????=????????时,四边形MNPQ为菱形
D.当M,N、P、Q是各边中点,且????????⊥????????时,四边形MNPQ为矩形
?
【详解】解:连接AC、BD交于点O,
∵M,N,P,Q是各边中点,∴????????∥????????,????????=12????????,????????∥????????,????????=12????????,
∴????????∥????????,????????=????????,∴四边MNPQ一定为平行四边形,A说法正确,不符合题意;
∠????????????=90?时,四边形MNPQ不一定为正方形,B说法错误,符合题意;
????????=????????时,????????=????????,∴四边形MNPQ为菱形,C说法正确,不符合题意;
????????⊥????????时,∠????????????=90?,
∴四边形MNPQ为矩形,D说法正确,不符合题意.
故选B.
?
5. 如图,点E、F、G、H分别是四边形ABCD的边AB、BC、CD、DA的中点.则下列说法:
①若AC=BD,则四边形EFGH为矩形;②若????????⊥????????,则四边形EFGH为菱形;
③若AC与BD互相垂直且相等,则四边形EFGH是正方形;④若四边形EFGH是平行四边形,则AC与BD互相平分.其中正确的个数是(????)
A.1 B.2 C.3 D.4
?
【详解】解:∵点E、F、G、H分别是四边形ABCD的边AB、BC、CD、DA的中点,
∴EH是△ABD的中位线,∴EH=12BD,EH∥BD,
同理GF=12BD,EF=12AC,GH=12AC,EF∥AC
∴EH=GF,GH=EF,∴四边形EFGH是平行四边形,
①若AC=BD,则EH=GF=GH=EF,则四边形EFGH是菱形,故①错误;
②若AC⊥BD,则EF⊥EH,∴平行四边形EFGH是矩形,故②错误;
③若AC与BD互相垂直且相等,结合①②的判断可知四边形EFGH是正方形,故③正确;
④若四边形EFGH是平行四边形,并不能推出AC与BD互相平分,故④错误,故选A.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
