2.2 有理数与无理数 课件(36张PPT)
文档属性
| 名称 | 2.2 有理数与无理数 课件(36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 37.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-10 16:26:57 | ||
图片预览









文档简介
2.2 有理数与无理数
第2章有理数
教学目标
01
认识有理数,理解有理数的两种定义方式
03
了解第一次数学危机,认识无理数,初步体会“逼近”思想
02
掌握有理数两大分类,并理解“六非问题”
有理数的概念
01
复习引入
1.整数与分数按正负性如何分类?
2.正整数与自然数有何关联?
整数
正整数
负整数
0
分数
正分数
负分数
自然数
01
复习引入
3.小数如何分类?
4.分数与小数有何关联?
小数
有限小数
无限小数
无限循环小数
无限不循环小数,例:π、1.010010001…
分数
01
问题引入
1.请列举几个分数,并总结分数的形式?
????????、???????? 、-???????????? 、???????????? ……
?
【总结】
分数的形式:????????(m、n是整数,n≠0)
?
01
问题引入
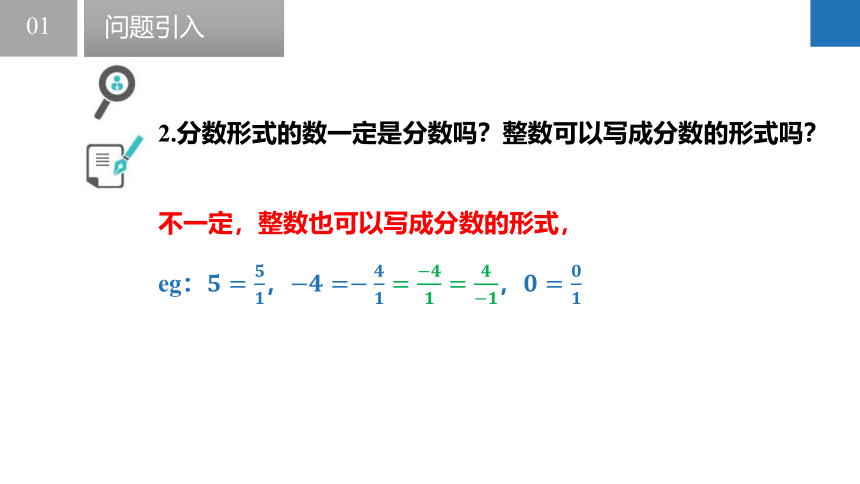
2.分数形式的数一定是分数吗?整数可以写成分数的形式吗?
不一定,整数也可以写成分数的形式,
eg:????=????????,?????=?????????=?????????=?????????,????=????????
?
02
二、定义
我们把能够写成分数形式????????(m、n是整数,n≠0)的数叫做有理数
?
知识精讲
有理数的概念
小明老师有几个问题想问大家
【总结】进一步,整数和分数统称为有理数
Yes,Yes,整数和分数都可以写成分数的形式
Q1:整数是有理数吗?分数是有理数吗?
02
二、定义
知识精讲
有理数的概念
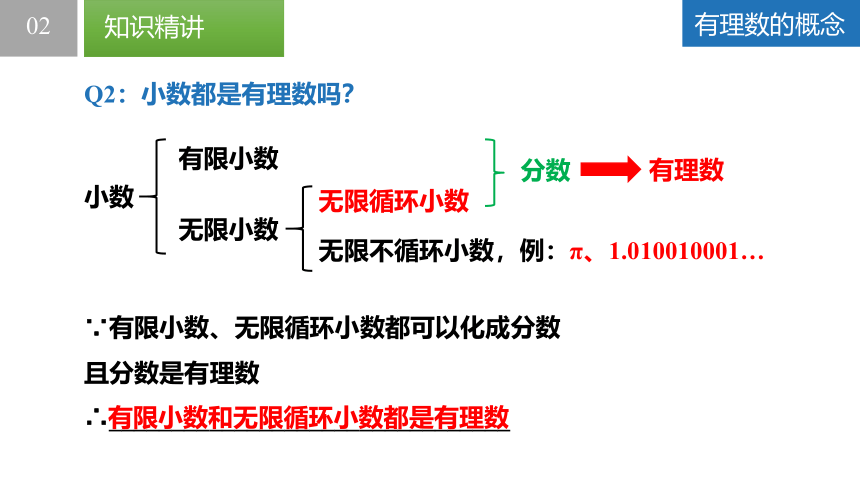
Q2:小数都是有理数吗?
小数
有限小数
无限小数
无限循环小数
无限不循环小数,例:π、1.010010001…
分数
有理数
∵有限小数、无限循环小数都可以化成分数
且分数是有理数
∴________________________________
有限小数和无限循环小数都是有理数
02
二、定义
知识精讲
有理数的概念
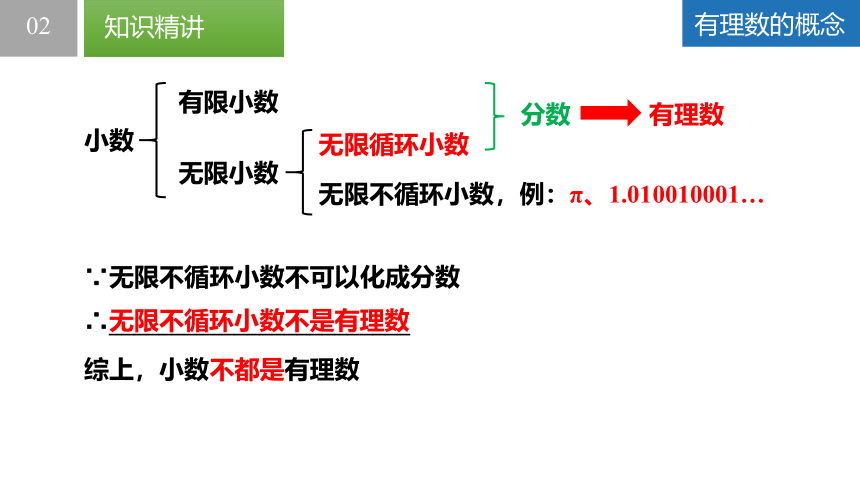
∵无限不循环小数不可以化成分数
∴________________________
无限不循环小数不是有理数
综上,小数不都是有理数
小数
有限小数
无限小数
无限循环小数
无限不循环小数,例:π、1.010010001…
分数
有理数
02
二、定义
知识精讲
有理数的概念
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}有理数
的两种定义
1.能够写成分数形式(m、n是整数,n≠0)的数
2.整数和分数统称为有理数
备注:有限小数和无限循环小数是有理数
无限不循环小数不是有理数
例1、在下列提供的数有?????????,-16,75%,????????????,0.1010010001…(相邻两个1之间依次增加一个0),3.14,0,-0.23333…中,属于分数的有( )个
A.2 B.3 C.4 D.5
?
03
典例精析
?????????看起来像分数,但其实不是,
π是无限不循环小数,?????????也是无限不循环小数
?
????????????=2,分数形式的数不一定是分数,整数也可以写成分数的形式
?
例1、在下列提供的数有?????????,-16,75%,????????????,0.1010010001…(相邻两个1之间依次增加一个0),3.14,0,-0.23333…中,属于分数的有( )个
A.2 B.3 C.4 D.5
?
03
典例精析
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}小数
小数的类型
是否为分数
是否为有理数
0.010010001
0.010101…
0.010010001…
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}小数的类型
是否为分数
是否为有理数
有限小数
√
√
无限循环小数
√
√
无限不循环小数
×
×
B
例2、在数0,3.141592653,?????????????,????+????????,0.????????,5.2%,2.020020002……(相邻两个2之间依次增加一个0)中有理数有( )个
A.5 B.4 C.3 D.2
?
03
典例精析
A
有理数的分类
有理数的两种分类
02
知识精讲
有理数的分类
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}先定义
后正负
请同学们按照要求对有理数进行分类
有理数
分数
整数
正整数
负整数
0
正分数
负分数
有理数
正有理数
负有理数
0
正整数
正分数
负整数
负分数
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}先正负
后定义
例1、把下列各数分别填入相应的框线内:
-10,6,-7????????,0,+3????????,-2.25,0.01,+67,-????????,10%,????????????????,2000,-18.
正整数:_________________________________________
负整数:_________________________________________
正分数:_________________________________________
负分数:_________________________________________
正有理数:_______________________________________
负有理数:_______________________________________
?
6,+67,2000.
-10,-18.
+3????????,0.01,10%,????????????????.
?
-7????????,-2.25,-????????.
?
6,+3????????,0.01,+67,10%,????????????????,2000.
?
-10,-7????????,-2.25,-????????,-18.
?
03
典例精析
例2、下列说法中,不正确的是( )
A.若一个数是整数,则它一定是有理数
B.若一个数不是有理数,则它一定不是整数
C.0既不是正有理数,也不是负有理数
D.正有理数和负有理数组成有理数
D
03
典例精析
有理数
正有理数
负有理数
0
例3、判断正误
(1)一个整数不是正数就是负数( )
(2)0是最小的有理数( )
(3)有最小的正整数,有最大的负整数 ( )
(4)有最小的正数,有最大的负数( )
-0.1<-0.000…1(中间有无数个0)<0<0.000…1(中间有无数个0)<0.1
负有理数<0
03
典例精析
√
×
最小的正整数是1,最大的负整数是-1
×
整数
正整数
负整数
0
×
现有 8 个有理数,已知其中有 4 个正数、3 个负数、5 个整数、1 个负分数,则正整数有( )个
A.0 B.1 C.2 D.3
C
04
超级挑战
有理数
分数
整数
正整数
负整数
0
正分数
负分数
8
5
1
2
2
1
“六非”问题
02
二、定义
知识精讲
“六非问题”
0和正数
0和负数——非正数
Q1:如果一个数不是正数,那么这个数是什么数 ?
Q2:非负数包含哪些数?
小明老师有几个问题想问大家
六非问题
02
二、定义
知识精讲
“六非问题”
非负有理数
0和正整数
自然数
Q3:非负整数包含哪些数?其“曾用名”是?
Q4:0和正有理数可以统称为?
注意断句
六非问题
二、6个“非”
口诀:见非写0,非后取反
02
知识精讲
六非问题
非正有理数:
非负有理数:
非正整数:
非负整数:
非正数:
非负数:
0+负整数
0+正整数
0+负有理数
0+正有理数
0+负数
0+正数
例1、请在下列表格中打?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
整数
分数
正数
负整数
正分数
非负数
非负整数
0
-2.5
-3
0.3
π
-
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
03
典例精析
例2、下列说法正确的是( )
A.非负整数就是正整数,非正整数就是负整数
B.非正整数就是除了正整数以外的所有数
C.0既是非负整数又是非正整数
D.没有最大的正整数,也没有最大的非正整数
C
0和
03
典例精析
0和
不是正的整数:
0和负整数
最大的非正整数是0
例3、填空
最小的非负整数是__________,
是负数而不是分数的有理数是__________,
是整数而不是正数的有理数是__________.
0
负整数
非正整数
03
典例精析
无理数的概念
02
二、定义
知识精讲
毕达哥拉斯学派认为:
“万物皆数”(即任何数都可以写成整数或整数与整数之比)
But one day,毕达哥拉斯的学生希帕索斯发现:
1
1
由于“????”不是整数,且无法写成整数与整数之比,
故第一次数学危机爆发!
?
无理数的概念
????
?
02
二、定义
知识精讲
再进一步,阅读课本P16
????——先暂时这样理解这个数——它的平方是2
?
∵1的平方=1,2的平方=4,
∴1?
∵1.4的平方=1.96,
1.5的平方=2.25,
∴1.4?
∵1.41的平方=1.9881,
1.42的平方=2.0164,
∴1.41?
……无限逼近……
无理数的概念
02
二、定义
我们把不能写成分数形式????????(m、n是整数,n≠0)的数叫做无理数,
即无限不循环小数叫做无理数
?
知识精讲
有理数的定义
无理数的概念
通过无限逼近,我们会发现,????的值是1.414213562373……
它是一个无限不循环小数,不能写成????????(m、n是整数,n≠0)的形式
?
eg:π、1.010010001…
02
二、定义
知识精讲
有理数的定义
无理数的概念
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}有理数
的两种定义
1.能够写成分数形式(m、n是整数,n≠0)的数
2.整数和分数统称为有理数
备注:有限小数和无限循环小数是有理数
无理数
的定义
无限不循环小数叫做无理数
例、下列数,属于无理数的是:__________.(填写序号)
(1)-6,(2)0.77777777,(3)0.3????,
(4)-????????,(5)0.303003003…(两个3之间依次多一个0),
(6)?????????????,(7)3.1415926,(8)0.80808…,(9)0.4040040004
?
(5)(6)
03
典例精析
无限不循环小数叫做无理数
课后总结
有理数
分数
整数
有理数
正有理数
负有理数
先定义,再正负
先正负,再定义
正整数
负整数
0
正分数
负分数
0
正整数
正分数
负整数
负分数
口诀:
见非写0,非后取反
非正有理数:
非负有理数:
非正整数:
非负整数:
非正数:
非负数:
0+负整数
0+正整数
0+负有理数
0+正有理数
0+负数
0+正数
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}有理数
的两种定义
1.能够写成分数形式(m、n是整数,n≠0)的数
2.整数和分数统称为有理数
备注:有限小数和无限循环小数是有理数
无理数
的定义
无限不循环小数叫做无理数
思维拓展
【思维拓展】自然数与正整数一样多吗?(不作要求)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}正整数
1
2
3
4
…
a
…
无穷大
自然数
0
1
2
3
a-1
…
无穷大-1
一一对应,故一样多
课后预习
正数比大小我们是会的,
那么负数如何比较大小呢?
需要借助什么样的工具呢?
请听下回分解~????
第2章有理数
教学目标
01
认识有理数,理解有理数的两种定义方式
03
了解第一次数学危机,认识无理数,初步体会“逼近”思想
02
掌握有理数两大分类,并理解“六非问题”
有理数的概念
01
复习引入
1.整数与分数按正负性如何分类?
2.正整数与自然数有何关联?
整数
正整数
负整数
0
分数
正分数
负分数
自然数
01
复习引入
3.小数如何分类?
4.分数与小数有何关联?
小数
有限小数
无限小数
无限循环小数
无限不循环小数,例:π、1.010010001…
分数
01
问题引入
1.请列举几个分数,并总结分数的形式?
????????、???????? 、-???????????? 、???????????? ……
?
【总结】
分数的形式:????????(m、n是整数,n≠0)
?
01
问题引入
2.分数形式的数一定是分数吗?整数可以写成分数的形式吗?
不一定,整数也可以写成分数的形式,
eg:????=????????,?????=?????????=?????????=?????????,????=????????
?
02
二、定义
我们把能够写成分数形式????????(m、n是整数,n≠0)的数叫做有理数
?
知识精讲
有理数的概念
小明老师有几个问题想问大家
【总结】进一步,整数和分数统称为有理数
Yes,Yes,整数和分数都可以写成分数的形式
Q1:整数是有理数吗?分数是有理数吗?
02
二、定义
知识精讲
有理数的概念
Q2:小数都是有理数吗?
小数
有限小数
无限小数
无限循环小数
无限不循环小数,例:π、1.010010001…
分数
有理数
∵有限小数、无限循环小数都可以化成分数
且分数是有理数
∴________________________________
有限小数和无限循环小数都是有理数
02
二、定义
知识精讲
有理数的概念
∵无限不循环小数不可以化成分数
∴________________________
无限不循环小数不是有理数
综上,小数不都是有理数
小数
有限小数
无限小数
无限循环小数
无限不循环小数,例:π、1.010010001…
分数
有理数
02
二、定义
知识精讲
有理数的概念
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}有理数
的两种定义
1.能够写成分数形式(m、n是整数,n≠0)的数
2.整数和分数统称为有理数
备注:有限小数和无限循环小数是有理数
无限不循环小数不是有理数
例1、在下列提供的数有?????????,-16,75%,????????????,0.1010010001…(相邻两个1之间依次增加一个0),3.14,0,-0.23333…中,属于分数的有( )个
A.2 B.3 C.4 D.5
?
03
典例精析
?????????看起来像分数,但其实不是,
π是无限不循环小数,?????????也是无限不循环小数
?
????????????=2,分数形式的数不一定是分数,整数也可以写成分数的形式
?
例1、在下列提供的数有?????????,-16,75%,????????????,0.1010010001…(相邻两个1之间依次增加一个0),3.14,0,-0.23333…中,属于分数的有( )个
A.2 B.3 C.4 D.5
?
03
典例精析
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}小数
小数的类型
是否为分数
是否为有理数
0.010010001
0.010101…
0.010010001…
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}小数的类型
是否为分数
是否为有理数
有限小数
√
√
无限循环小数
√
√
无限不循环小数
×
×
B
例2、在数0,3.141592653,?????????????,????+????????,0.????????,5.2%,2.020020002……(相邻两个2之间依次增加一个0)中有理数有( )个
A.5 B.4 C.3 D.2
?
03
典例精析
A
有理数的分类
有理数的两种分类
02
知识精讲
有理数的分类
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}先定义
后正负
请同学们按照要求对有理数进行分类
有理数
分数
整数
正整数
负整数
0
正分数
负分数
有理数
正有理数
负有理数
0
正整数
正分数
负整数
负分数
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}先正负
后定义
例1、把下列各数分别填入相应的框线内:
-10,6,-7????????,0,+3????????,-2.25,0.01,+67,-????????,10%,????????????????,2000,-18.
正整数:_________________________________________
负整数:_________________________________________
正分数:_________________________________________
负分数:_________________________________________
正有理数:_______________________________________
负有理数:_______________________________________
?
6,+67,2000.
-10,-18.
+3????????,0.01,10%,????????????????.
?
-7????????,-2.25,-????????.
?
6,+3????????,0.01,+67,10%,????????????????,2000.
?
-10,-7????????,-2.25,-????????,-18.
?
03
典例精析
例2、下列说法中,不正确的是( )
A.若一个数是整数,则它一定是有理数
B.若一个数不是有理数,则它一定不是整数
C.0既不是正有理数,也不是负有理数
D.正有理数和负有理数组成有理数
D
03
典例精析
有理数
正有理数
负有理数
0
例3、判断正误
(1)一个整数不是正数就是负数( )
(2)0是最小的有理数( )
(3)有最小的正整数,有最大的负整数 ( )
(4)有最小的正数,有最大的负数( )
-0.1<-0.000…1(中间有无数个0)<0<0.000…1(中间有无数个0)<0.1
负有理数<0
03
典例精析
√
×
最小的正整数是1,最大的负整数是-1
×
整数
正整数
负整数
0
×
现有 8 个有理数,已知其中有 4 个正数、3 个负数、5 个整数、1 个负分数,则正整数有( )个
A.0 B.1 C.2 D.3
C
04
超级挑战
有理数
分数
整数
正整数
负整数
0
正分数
负分数
8
5
1
2
2
1
“六非”问题
02
二、定义
知识精讲
“六非问题”
0和正数
0和负数——非正数
Q1:如果一个数不是正数,那么这个数是什么数 ?
Q2:非负数包含哪些数?
小明老师有几个问题想问大家
六非问题
02
二、定义
知识精讲
“六非问题”
非负有理数
0和正整数
自然数
Q3:非负整数包含哪些数?其“曾用名”是?
Q4:0和正有理数可以统称为?
注意断句
六非问题
二、6个“非”
口诀:见非写0,非后取反
02
知识精讲
六非问题
非正有理数:
非负有理数:
非正整数:
非负整数:
非正数:
非负数:
0+负整数
0+正整数
0+负有理数
0+正有理数
0+负数
0+正数
例1、请在下列表格中打?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
整数
分数
正数
负整数
正分数
非负数
非负整数
0
-2.5
-3
0.3
π
-
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
03
典例精析
例2、下列说法正确的是( )
A.非负整数就是正整数,非正整数就是负整数
B.非正整数就是除了正整数以外的所有数
C.0既是非负整数又是非正整数
D.没有最大的正整数,也没有最大的非正整数
C
0和
03
典例精析
0和
不是正的整数:
0和负整数
最大的非正整数是0
例3、填空
最小的非负整数是__________,
是负数而不是分数的有理数是__________,
是整数而不是正数的有理数是__________.
0
负整数
非正整数
03
典例精析
无理数的概念
02
二、定义
知识精讲
毕达哥拉斯学派认为:
“万物皆数”(即任何数都可以写成整数或整数与整数之比)
But one day,毕达哥拉斯的学生希帕索斯发现:
1
1
由于“????”不是整数,且无法写成整数与整数之比,
故第一次数学危机爆发!
?
无理数的概念
????
?
02
二、定义
知识精讲
再进一步,阅读课本P16
????——先暂时这样理解这个数——它的平方是2
?
∵1的平方=1,2的平方=4,
∴1?
∵1.4的平方=1.96,
1.5的平方=2.25,
∴1.4?
∵1.41的平方=1.9881,
1.42的平方=2.0164,
∴1.41?
……无限逼近……
无理数的概念
02
二、定义
我们把不能写成分数形式????????(m、n是整数,n≠0)的数叫做无理数,
即无限不循环小数叫做无理数
?
知识精讲
有理数的定义
无理数的概念
通过无限逼近,我们会发现,????的值是1.414213562373……
它是一个无限不循环小数,不能写成????????(m、n是整数,n≠0)的形式
?
eg:π、1.010010001…
02
二、定义
知识精讲
有理数的定义
无理数的概念
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}有理数
的两种定义
1.能够写成分数形式(m、n是整数,n≠0)的数
2.整数和分数统称为有理数
备注:有限小数和无限循环小数是有理数
无理数
的定义
无限不循环小数叫做无理数
例、下列数,属于无理数的是:__________.(填写序号)
(1)-6,(2)0.77777777,(3)0.3????,
(4)-????????,(5)0.303003003…(两个3之间依次多一个0),
(6)?????????????,(7)3.1415926,(8)0.80808…,(9)0.4040040004
?
(5)(6)
03
典例精析
无限不循环小数叫做无理数
课后总结
有理数
分数
整数
有理数
正有理数
负有理数
先定义,再正负
先正负,再定义
正整数
负整数
0
正分数
负分数
0
正整数
正分数
负整数
负分数
口诀:
见非写0,非后取反
非正有理数:
非负有理数:
非正整数:
非负整数:
非正数:
非负数:
0+负整数
0+正整数
0+负有理数
0+正有理数
0+负数
0+正数
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}有理数
的两种定义
1.能够写成分数形式(m、n是整数,n≠0)的数
2.整数和分数统称为有理数
备注:有限小数和无限循环小数是有理数
无理数
的定义
无限不循环小数叫做无理数
思维拓展
【思维拓展】自然数与正整数一样多吗?(不作要求)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}正整数
1
2
3
4
…
a
…
无穷大
自然数
0
1
2
3
a-1
…
无穷大-1
一一对应,故一样多
课后预习
正数比大小我们是会的,
那么负数如何比较大小呢?
需要借助什么样的工具呢?
请听下回分解~????
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
