2.4圆周角(第3课时) 课件(30张PPT)
文档属性
| 名称 | 2.4圆周角(第3课时) 课件(30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-10 16:35:14 | ||
图片预览




文档简介
第2章 · 对称图形——圆
2.4 圆周角
第3课时 圆的内接四边形
1.知道圆的内接四边形和四边形的外接圆的概念;
2.理解圆内接四边形的性质;
3.会利用圆内接四边形的性质进行简单计算和证明.
学习目标
知识回顾
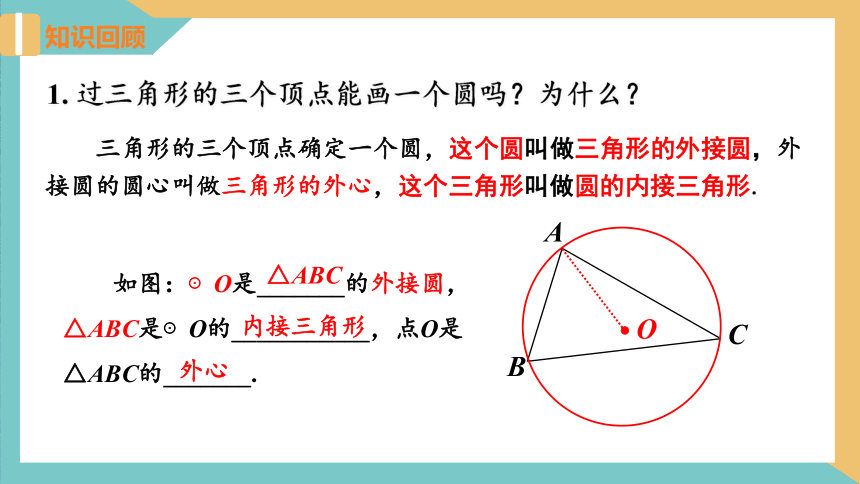
1. 过三角形的三个顶点能画一个圆吗?为什么?
C
A
B
O
三角形的三个顶点确定一个圆,这个圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
如图:⊙O是_______的外接圆, △ABC是⊙O的___________,点O是△ABC的_______.
△ABC
内接三角形
外心
B
C
A
知识回顾
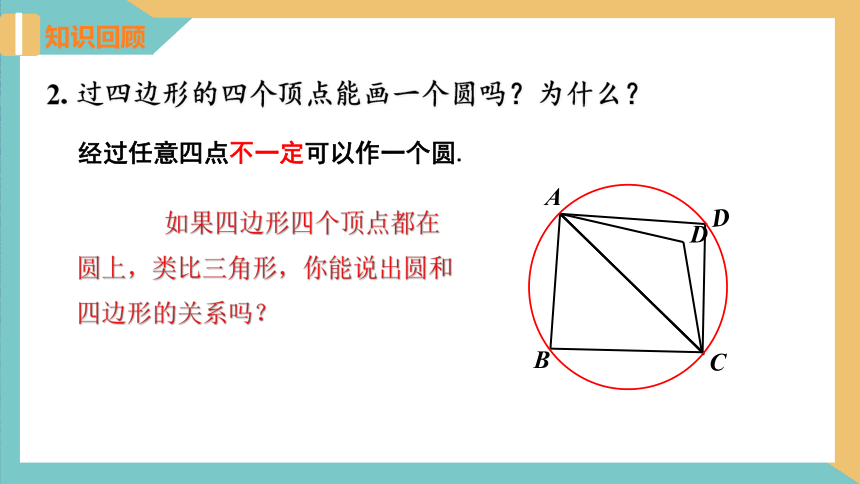
2. 过四边形的四个顶点能画一个圆吗?为什么?
经过任意四点不一定可以作一个圆.
D
D
如果四边形四个顶点都在圆上,类比三角形,你能说出圆和四边形的关系吗?
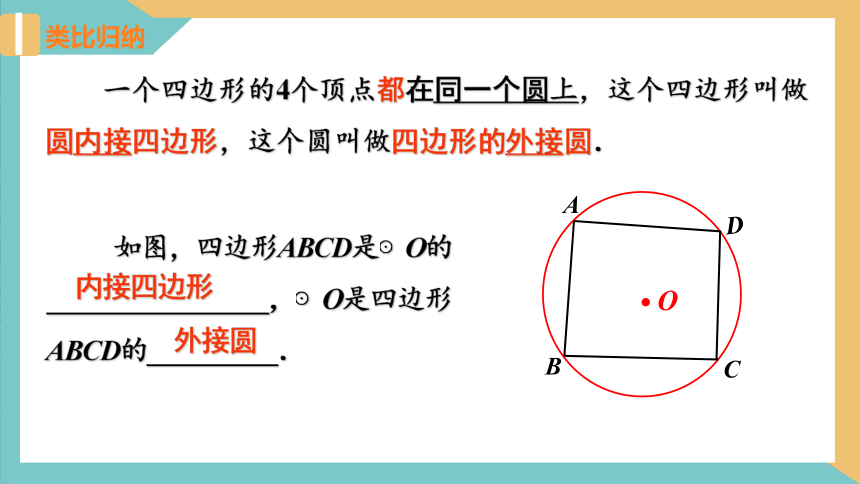
类比归纳
B
C
A
D
一个四边形的4个顶点都在同一个圆上,这个四边形叫做圆内接四边形,这个圆叫做四边形的外接圆.
O
如图,四边形ABCD是⊙O的_________________,⊙O是四边形ABCD的__________.
内接四边形
外接圆
┐
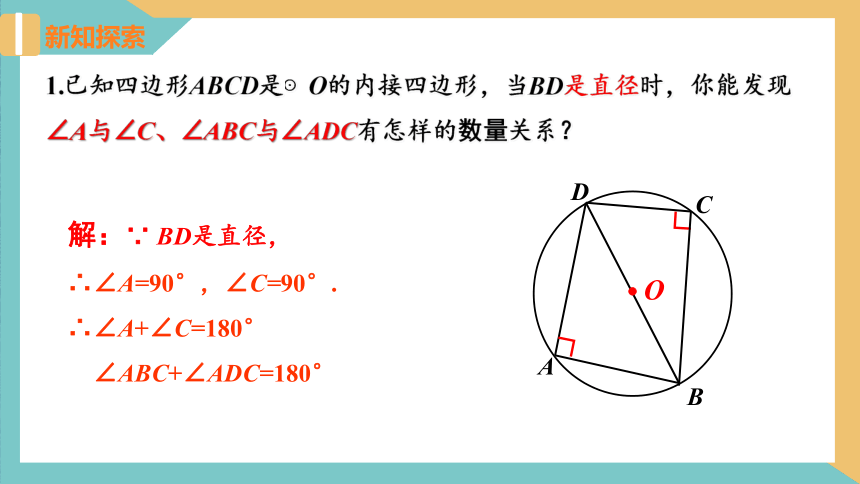
新知探索
A
B
D
O
┐
C
1.已知四边形ABCD是⊙O的内接四边形,当BD是直径时,你能发现∠A与∠C、∠ABC与∠ADC有怎样的数量关系?
解:∵ BD是直径,
∴∠A=90°,∠C=90°.
∴∠A+∠C=180°
∠ABC+∠ADC=180°
2.已知四边形ABCD是⊙O的内接四边形,当BD不是直径时,你上面发现的∠A与∠C、∠ABC与∠ADC的数量关系是否依然成立?为什么?
新知探索
A
B
D
O
C
E
解:作直径DE,连接AE,CE.
∵∠ABC=∠ABD+∠DBC
∠AEC=∠AED+∠DEC
∠AED=∠ABD , ∠DEC=∠DBC
∴∠ABC=∠AEC
∵∠AEC+∠ADC=180°
∴∠ABC+∠ADC=180°
想想还有其他方法吗?
新知探索
A
B
D
O
C
解: ∵∠ABC=???????? ????????????的度数
?
∠ADC=???????? ????????????的度数
?
∴ ∠ADC+∠ABC
=????????(????????????的度数+????????????的度数)
=180°
?
请你归纳总结上面的发现,你能否将结论表述出来?
新知归纳
A
B
D
O
C
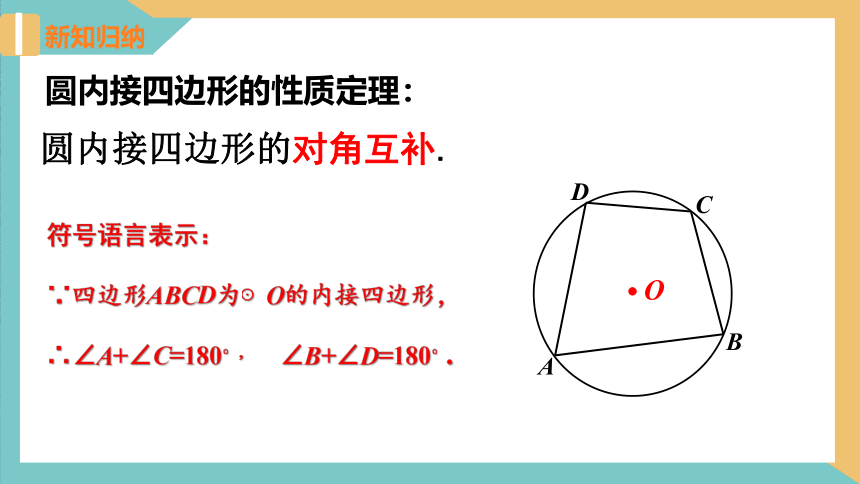
圆内接四边形的性质定理:
圆内接四边形的对角互补.
符号语言表示:
∵四边形ABCD为⊙O的内接四边形,
∴∠A+∠C=180?, ∠B+∠D=180?.
新知应用
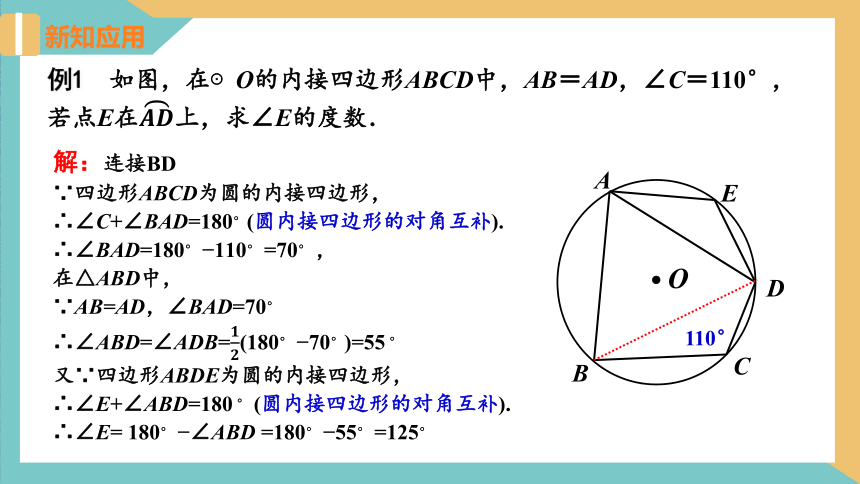
例1 如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=110°,若点E在????????上,求∠E的度数.
?
B
D
A
O
E
C
解:连接BD
∵四边形ABCD为圆的内接四边形,
∴∠C+∠BAD=180?(圆内接四边形的对角互补).
∴∠BAD=180? ?110? =70? ,
在△ABD中,
∵AB=AD,∠BAD=70?
∴∠ABD=∠ADB=????????(180? ?70?)=55 ?
又∵四边形ABDE为圆的内接四边形,
∴∠E+∠ABD=180 ? (圆内接四边形的对角互补).
∴∠E= 180? ?∠ABD =180? ?55? =125?
?
110°
新知巩固
C
A
B
O
E
D
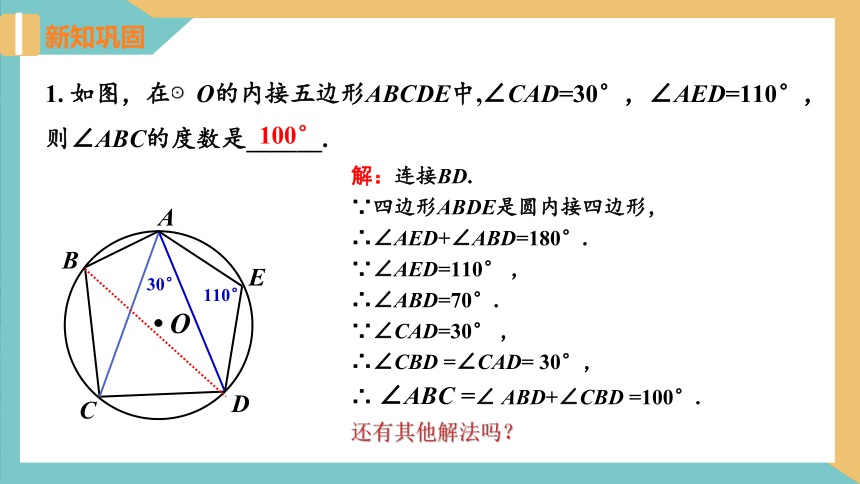
1. 如图,在⊙O的内接五边形ABCDE中,∠CAD=30°,∠AED=110°,则∠ABC的度数是______.
30°
110°
解:连接BD.
∵四边形ABDE是圆内接四边形,
∴∠AED+∠ABD=180°.
∵∠AED=110° ,
∴∠ABD=70°.
∵∠CAD=30° ,
∴∠CBD =∠CAD= 30°,
∴ ∠ABC =∠ ABD+∠CBD =100°.
100°
还有其他解法吗?
新知巩固
B
D
A
O
E
C
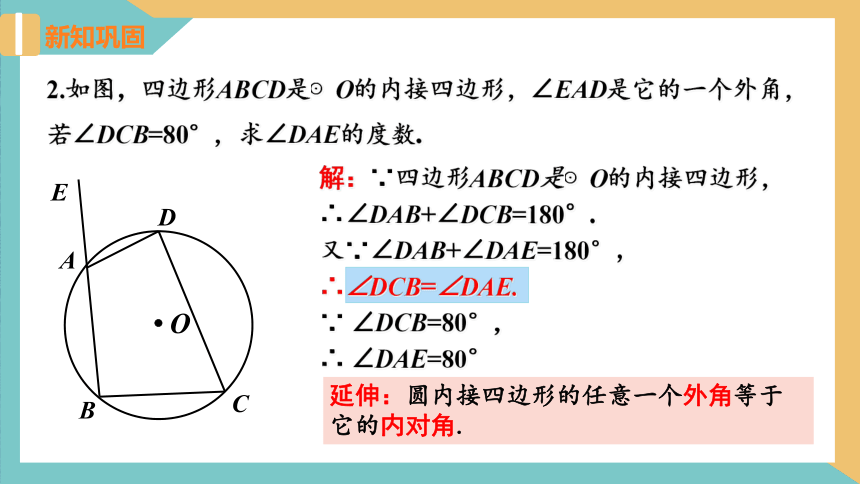
2.如图,四边形ABCD是⊙O的内接四边形,∠EAD是它的一个外角,若∠DCB=80°,求∠DAE的度数.
解:∵四边形ABCD是⊙O的内接四边形,
∴∠DAB+∠DCB=180°.
又∵∠DAB+∠DAE=180°,
∴∠DCB=∠DAE.
∵ ∠DCB=80°,
∴ ∠DAE=80°
延伸:圆内接四边形的任意一个外角等于它的内对角.
新知巩固
B
D
A
O
E
C
变式1 连接DB、AC,若 DB=DC,∠DAE与∠DAC相等吗?为什么?
√
√
解:相等.
理由如下:
∵四边形ABCD是⊙O的内接四边形,
∴∠DAB+∠DCB=180°
又∵∠DAB+∠DAE=180°
∴∠DCB= ∠DAE
∵DB=DC
∴∠DCB= ∠DBC
又∵ ∠DAC= ∠DBC = ∠DCB
∴∠DAE=∠DAC
新知巩固
变式2 如图,AD为圆内接三角形ABC的外角∠EAC的平分线,它与圆交于点D,连接DB、DC.
(1)求证:△DBC是等腰三角形;
B
D
A
O
E
C
(1)证明:∵AD是∠EAC的角平分线,
∴∠DAE=∠DAC.
∵ ????????=?????????,
∴∠DBC=∠DAC,
∵ ∠DCB=∠DAE(已证),
∴∠DBC=∠DCB.
∴ DB=DC.
∴ △DBC是等腰三角形.
?
新知巩固
(2) F为BC上一点,请你再补充一个条件使直线DF一定经过圆心,并说明理由.
B
D
A
O
E
C
F
(2)解:若F为BC中点,则DF经过圆心.
∵△DBC是等腰三角形, F为BC中点,
∴DF是BC边上的中垂线.
∵圆内接三角形圆心是三边中垂线的交点,
∴DF必过圆心.
课堂小结
圆内接四边形的性质定理:
圆内接四边形的对角互补.
推论:圆内接四边形的任意一个外角等于它的内对角.
当堂检测
1.下列关于圆内接四边形的叙述正确的有( )
①圆内接四边形的任意一个外角都等于它的内对角;
②圆内接四边形对角相等;
③圆内接四边形中不相邻的两个内角互补;
④在圆内部的四边形叫做圆内接四边形.
A.1个 B.2个 C.3个 D.4个
B
当堂检测
2.有下列命题:
① 圆内接平行四边形是矩形;
② 圆内接矩形是正方形;
③ 圆内接菱形是正方形.
其中,真命题是( )
D
A. ①②
B. ①②③
C. ②③
D. ①③
当堂检测
3.如图,四边形ABCD内接于⊙O,若∠A=40°,则∠C=( )
A.110° B.120° C.135° D.140°
B
D
A
O
C
D
当堂检测
4.如图,四边形ABCD是☉O的内接四边形,若∠BCD=121°,则∠BOD的度数为( )
A. 138°
B. 121°
C. 118°
D. 112°
C
B
D
A
O
C
当堂检测
5. 在四边形ABCD中,∠A、∠B、∠C、∠D的度数之比为2:3:4:3,则∠C的外角等于( )
A. 60° B. 75° C. 90° D. 120°
A
6.在⊙O中,弦AB等于半径,则AB所对的圆周角的度数为____________.
30°或150°
注意两种情况.
当堂检测
7.如图,在圆内接四边形ABCD中,若∠A∶∠B∶∠C=4∶3∶5,则∠D的度数是? 120?.
120°
A
C
D
O
B
当堂检测
A
C
D
O
B
8.如图,四边形ABCD为☉O的内接四边形,∠C=∠D,则AB与CD的位置关系是? AB∥CD ?.?
AB∥CD
当堂检测
9.如图,四边形ABCD内接于☉O,∠ABC=60°,对角线DB平分∠ADC.
(1)求证:△ABC是等边三角形;
解:(1) ∵ 四边形ABCD内接于☉O,
∴ ∠ABC+∠ADC=180°.
∵ ∠ABC=60°,
∴ ∠ADC=120°.
∵ DB平分∠ADC,
∴ ∠ADB=∠CDB=60°.
∵ ????????=????????,????????=????????,
∴ ∠ACB=∠ADB=60°,∠BAC=∠CDB=60°
.∴ ∠ABC=∠ACB=∠BAC.
∴ △ABC是等边三角形
?
C
B
A
O
D
当堂检测
(2)若AD=2,DC=3,求△ABC的周长.
解:(2) 如图,过点A作AM⊥CD,交CD的延长线于点M.
∴ ∠AMD=90°.
∵ ∠ADC=120°,∠MDC=180°,
∴ ∠ADM=60°.
∴ 在Rt△AMD中,∠DAM=30°.
∴ 易得DM=????????AD=1.
∴ AM=?????????????????????????=????.
∵ CD=3,
∴ CM=CD+DM=4.
∴ 在Rt△AMC中, AC=????????????+????????????=????????.
∵ △ABC是等边三角形,
∴ AB=AC=BC=????????.
∴ △ABC的周长为3????????
?
C
B
A
O
D
M
┐
当堂检测
10. 如图,☉O1和☉O2都经过A、B两点.经过点A的直线CD交☉O1于点C,交☉O2于点D;经过点B的直线EF交☉O1于点E,交☉O2于点F.试判断CE与DF是否平行,并说明理由.
C
D
A
B
E
O1
F
O2
解:CE与DF平行
理由:连接AB.
∵ 四边形ABEC是☉O1的内接四边形,
∴ ∠BAC+∠E=180°.
∵ ∠BAC+∠BAD=180°,
∴ ∠BAD=∠E.
∵ 四边形ABFD是☉O2的内接四边形,
∴ ∠BAD+∠F=180°.
∴ ∠E+∠F=180°.
∴ CE∥DF.
当堂检测
11.如图,四边形ABCD内接于☉O,AD是☉O的直径,C是????????的中点,AB和DC的延长线交☉O外一点E.求证:BC=EC.
?
C
B
E
O
D
1
2
A
解:如图,连接AC.
∵AD是☉O的直径,
∴∠ACD=∠ACE=90°.
∵四边形ABCD内接于☉O,
∴∠D+∠ABC=180°.
∵∠ABC+∠EBC=180°,
∴∠EBC=∠D.
∵C是????????的中点,
∴∠1=∠2.
又∵∠1+∠E=∠2+∠D=90°,
∴∠E=∠D.
∴∠EBC=∠E.∴BC=EC
?
12.如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F.
(1)当∠E=∠F时,则∠ADC=__________;
当堂检测
90°
A
C
D
O
B
E
F
12.如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F.
(2)当∠A=55°,∠E=30°时,求∠F的度数;
当堂检测
A
C
D
O
B
E
F
55°
30°
解:(2)∵∠A=55°,∠E=30°,
∴∠ABE=180°-∠A-∠E=95°,
∴∠ADF=180°-∠ABE=85°,
∴∠F=180°-∠ADF-∠A=40°.
12.如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F.
(3)若∠E=α,∠F=β,且α≠β.请你用含有α、β的代数式表示∠A的大小.
当堂检测
解:(3)∵∠ADC=180°-∠A-∠F,
∠ABC=180°-∠A-∠E,
∠ADC+∠ABC=180°,
∴180°-∠A-∠F+180°-∠A-∠E=180°,
∴2∠A+∠E+∠F=180°,
∴∠A=90°-∠????+∠????????=90°- ????+????????.
?
A
C
D
O
B
E
F
2.4 圆周角
第3课时 圆的内接四边形
1.知道圆的内接四边形和四边形的外接圆的概念;
2.理解圆内接四边形的性质;
3.会利用圆内接四边形的性质进行简单计算和证明.
学习目标
知识回顾
1. 过三角形的三个顶点能画一个圆吗?为什么?
C
A
B
O
三角形的三个顶点确定一个圆,这个圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
如图:⊙O是_______的外接圆, △ABC是⊙O的___________,点O是△ABC的_______.
△ABC
内接三角形
外心
B
C
A
知识回顾
2. 过四边形的四个顶点能画一个圆吗?为什么?
经过任意四点不一定可以作一个圆.
D
D
如果四边形四个顶点都在圆上,类比三角形,你能说出圆和四边形的关系吗?
类比归纳
B
C
A
D
一个四边形的4个顶点都在同一个圆上,这个四边形叫做圆内接四边形,这个圆叫做四边形的外接圆.
O
如图,四边形ABCD是⊙O的_________________,⊙O是四边形ABCD的__________.
内接四边形
外接圆
┐
新知探索
A
B
D
O
┐
C
1.已知四边形ABCD是⊙O的内接四边形,当BD是直径时,你能发现∠A与∠C、∠ABC与∠ADC有怎样的数量关系?
解:∵ BD是直径,
∴∠A=90°,∠C=90°.
∴∠A+∠C=180°
∠ABC+∠ADC=180°
2.已知四边形ABCD是⊙O的内接四边形,当BD不是直径时,你上面发现的∠A与∠C、∠ABC与∠ADC的数量关系是否依然成立?为什么?
新知探索
A
B
D
O
C
E
解:作直径DE,连接AE,CE.
∵∠ABC=∠ABD+∠DBC
∠AEC=∠AED+∠DEC
∠AED=∠ABD , ∠DEC=∠DBC
∴∠ABC=∠AEC
∵∠AEC+∠ADC=180°
∴∠ABC+∠ADC=180°
想想还有其他方法吗?
新知探索
A
B
D
O
C
解: ∵∠ABC=???????? ????????????的度数
?
∠ADC=???????? ????????????的度数
?
∴ ∠ADC+∠ABC
=????????(????????????的度数+????????????的度数)
=180°
?
请你归纳总结上面的发现,你能否将结论表述出来?
新知归纳
A
B
D
O
C
圆内接四边形的性质定理:
圆内接四边形的对角互补.
符号语言表示:
∵四边形ABCD为⊙O的内接四边形,
∴∠A+∠C=180?, ∠B+∠D=180?.
新知应用
例1 如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=110°,若点E在????????上,求∠E的度数.
?
B
D
A
O
E
C
解:连接BD
∵四边形ABCD为圆的内接四边形,
∴∠C+∠BAD=180?(圆内接四边形的对角互补).
∴∠BAD=180? ?110? =70? ,
在△ABD中,
∵AB=AD,∠BAD=70?
∴∠ABD=∠ADB=????????(180? ?70?)=55 ?
又∵四边形ABDE为圆的内接四边形,
∴∠E+∠ABD=180 ? (圆内接四边形的对角互补).
∴∠E= 180? ?∠ABD =180? ?55? =125?
?
110°
新知巩固
C
A
B
O
E
D
1. 如图,在⊙O的内接五边形ABCDE中,∠CAD=30°,∠AED=110°,则∠ABC的度数是______.
30°
110°
解:连接BD.
∵四边形ABDE是圆内接四边形,
∴∠AED+∠ABD=180°.
∵∠AED=110° ,
∴∠ABD=70°.
∵∠CAD=30° ,
∴∠CBD =∠CAD= 30°,
∴ ∠ABC =∠ ABD+∠CBD =100°.
100°
还有其他解法吗?
新知巩固
B
D
A
O
E
C
2.如图,四边形ABCD是⊙O的内接四边形,∠EAD是它的一个外角,若∠DCB=80°,求∠DAE的度数.
解:∵四边形ABCD是⊙O的内接四边形,
∴∠DAB+∠DCB=180°.
又∵∠DAB+∠DAE=180°,
∴∠DCB=∠DAE.
∵ ∠DCB=80°,
∴ ∠DAE=80°
延伸:圆内接四边形的任意一个外角等于它的内对角.
新知巩固
B
D
A
O
E
C
变式1 连接DB、AC,若 DB=DC,∠DAE与∠DAC相等吗?为什么?
√
√
解:相等.
理由如下:
∵四边形ABCD是⊙O的内接四边形,
∴∠DAB+∠DCB=180°
又∵∠DAB+∠DAE=180°
∴∠DCB= ∠DAE
∵DB=DC
∴∠DCB= ∠DBC
又∵ ∠DAC= ∠DBC = ∠DCB
∴∠DAE=∠DAC
新知巩固
变式2 如图,AD为圆内接三角形ABC的外角∠EAC的平分线,它与圆交于点D,连接DB、DC.
(1)求证:△DBC是等腰三角形;
B
D
A
O
E
C
(1)证明:∵AD是∠EAC的角平分线,
∴∠DAE=∠DAC.
∵ ????????=?????????,
∴∠DBC=∠DAC,
∵ ∠DCB=∠DAE(已证),
∴∠DBC=∠DCB.
∴ DB=DC.
∴ △DBC是等腰三角形.
?
新知巩固
(2) F为BC上一点,请你再补充一个条件使直线DF一定经过圆心,并说明理由.
B
D
A
O
E
C
F
(2)解:若F为BC中点,则DF经过圆心.
∵△DBC是等腰三角形, F为BC中点,
∴DF是BC边上的中垂线.
∵圆内接三角形圆心是三边中垂线的交点,
∴DF必过圆心.
课堂小结
圆内接四边形的性质定理:
圆内接四边形的对角互补.
推论:圆内接四边形的任意一个外角等于它的内对角.
当堂检测
1.下列关于圆内接四边形的叙述正确的有( )
①圆内接四边形的任意一个外角都等于它的内对角;
②圆内接四边形对角相等;
③圆内接四边形中不相邻的两个内角互补;
④在圆内部的四边形叫做圆内接四边形.
A.1个 B.2个 C.3个 D.4个
B
当堂检测
2.有下列命题:
① 圆内接平行四边形是矩形;
② 圆内接矩形是正方形;
③ 圆内接菱形是正方形.
其中,真命题是( )
D
A. ①②
B. ①②③
C. ②③
D. ①③
当堂检测
3.如图,四边形ABCD内接于⊙O,若∠A=40°,则∠C=( )
A.110° B.120° C.135° D.140°
B
D
A
O
C
D
当堂检测
4.如图,四边形ABCD是☉O的内接四边形,若∠BCD=121°,则∠BOD的度数为( )
A. 138°
B. 121°
C. 118°
D. 112°
C
B
D
A
O
C
当堂检测
5. 在四边形ABCD中,∠A、∠B、∠C、∠D的度数之比为2:3:4:3,则∠C的外角等于( )
A. 60° B. 75° C. 90° D. 120°
A
6.在⊙O中,弦AB等于半径,则AB所对的圆周角的度数为____________.
30°或150°
注意两种情况.
当堂检测
7.如图,在圆内接四边形ABCD中,若∠A∶∠B∶∠C=4∶3∶5,则∠D的度数是? 120?.
120°
A
C
D
O
B
当堂检测
A
C
D
O
B
8.如图,四边形ABCD为☉O的内接四边形,∠C=∠D,则AB与CD的位置关系是? AB∥CD ?.?
AB∥CD
当堂检测
9.如图,四边形ABCD内接于☉O,∠ABC=60°,对角线DB平分∠ADC.
(1)求证:△ABC是等边三角形;
解:(1) ∵ 四边形ABCD内接于☉O,
∴ ∠ABC+∠ADC=180°.
∵ ∠ABC=60°,
∴ ∠ADC=120°.
∵ DB平分∠ADC,
∴ ∠ADB=∠CDB=60°.
∵ ????????=????????,????????=????????,
∴ ∠ACB=∠ADB=60°,∠BAC=∠CDB=60°
.∴ ∠ABC=∠ACB=∠BAC.
∴ △ABC是等边三角形
?
C
B
A
O
D
当堂检测
(2)若AD=2,DC=3,求△ABC的周长.
解:(2) 如图,过点A作AM⊥CD,交CD的延长线于点M.
∴ ∠AMD=90°.
∵ ∠ADC=120°,∠MDC=180°,
∴ ∠ADM=60°.
∴ 在Rt△AMD中,∠DAM=30°.
∴ 易得DM=????????AD=1.
∴ AM=?????????????????????????=????.
∵ CD=3,
∴ CM=CD+DM=4.
∴ 在Rt△AMC中, AC=????????????+????????????=????????.
∵ △ABC是等边三角形,
∴ AB=AC=BC=????????.
∴ △ABC的周长为3????????
?
C
B
A
O
D
M
┐
当堂检测
10. 如图,☉O1和☉O2都经过A、B两点.经过点A的直线CD交☉O1于点C,交☉O2于点D;经过点B的直线EF交☉O1于点E,交☉O2于点F.试判断CE与DF是否平行,并说明理由.
C
D
A
B
E
O1
F
O2
解:CE与DF平行
理由:连接AB.
∵ 四边形ABEC是☉O1的内接四边形,
∴ ∠BAC+∠E=180°.
∵ ∠BAC+∠BAD=180°,
∴ ∠BAD=∠E.
∵ 四边形ABFD是☉O2的内接四边形,
∴ ∠BAD+∠F=180°.
∴ ∠E+∠F=180°.
∴ CE∥DF.
当堂检测
11.如图,四边形ABCD内接于☉O,AD是☉O的直径,C是????????的中点,AB和DC的延长线交☉O外一点E.求证:BC=EC.
?
C
B
E
O
D
1
2
A
解:如图,连接AC.
∵AD是☉O的直径,
∴∠ACD=∠ACE=90°.
∵四边形ABCD内接于☉O,
∴∠D+∠ABC=180°.
∵∠ABC+∠EBC=180°,
∴∠EBC=∠D.
∵C是????????的中点,
∴∠1=∠2.
又∵∠1+∠E=∠2+∠D=90°,
∴∠E=∠D.
∴∠EBC=∠E.∴BC=EC
?
12.如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F.
(1)当∠E=∠F时,则∠ADC=__________;
当堂检测
90°
A
C
D
O
B
E
F
12.如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F.
(2)当∠A=55°,∠E=30°时,求∠F的度数;
当堂检测
A
C
D
O
B
E
F
55°
30°
解:(2)∵∠A=55°,∠E=30°,
∴∠ABE=180°-∠A-∠E=95°,
∴∠ADF=180°-∠ABE=85°,
∴∠F=180°-∠ADF-∠A=40°.
12.如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F.
(3)若∠E=α,∠F=β,且α≠β.请你用含有α、β的代数式表示∠A的大小.
当堂检测
解:(3)∵∠ADC=180°-∠A-∠F,
∠ABC=180°-∠A-∠E,
∠ADC+∠ABC=180°,
∴180°-∠A-∠F+180°-∠A-∠E=180°,
∴2∠A+∠E+∠F=180°,
∴∠A=90°-∠????+∠????????=90°- ????+????????.
?
A
C
D
O
B
E
F
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
