第11章 三角形复习与小结 课件(24张PPT)
文档属性
| 名称 | 第11章 三角形复习与小结 课件(24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 668.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-10 16:38:58 | ||
图片预览







文档简介
(共24张PPT)
第11章三角形复习与小结
人教版数学八年级上册
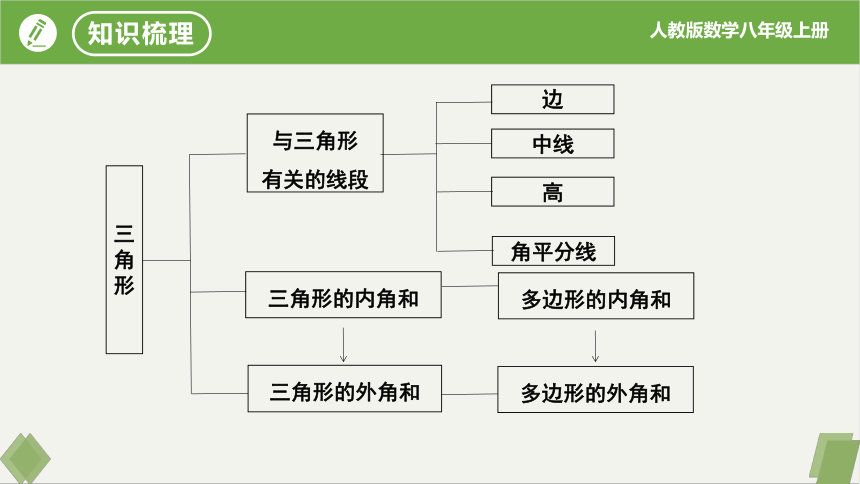
三角形
边
与三角形
有关的线段
三角形的内角和
三角形的外角和
多边形的内角和
多边形的外角和
中线
高
角平分线
知识梳理
知识点一与三角形有关的线段
1、三角形的三边关系
三角形两边之和大于第三边,三角形两边之差小于第三边.
2、三角形的高、中线、角平分线的定义
从三角形的一个顶点向它所对的边所在直线画垂线,顶点与垂足之间的线段叫做三角形的这条边上的高.
连接三角形的一个顶点和它所对的边的中点,所得线段叫做三角形这条边上的中线.
三角形一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.
知识梳理
3、三角形的重心
三角形的三条中线的交点叫做三角形的重心.
4、三角形的稳定性
三角形具有稳定性,四边形具有不稳定性.
知识点一与三角形有关的线段
知识梳理
1.下列各组线段能构成三角形的是( )
A.2cm,3cm,7cm B.5cm,3cm,10cm
C.3cm,4cm,7cm D.5cm,6cm,9cm
D
A.2+3<7,不能构成三角形.
B.5+3<10,不能构成三角形.
C.3+4=7,不能构成三角形.
D.5+6>9,可以构成三角形.
判断三条线段是否可以构成
三角形,只需根据“两条较短的线段之和大于第三条线段”判断即可.
课堂检测
课堂检测
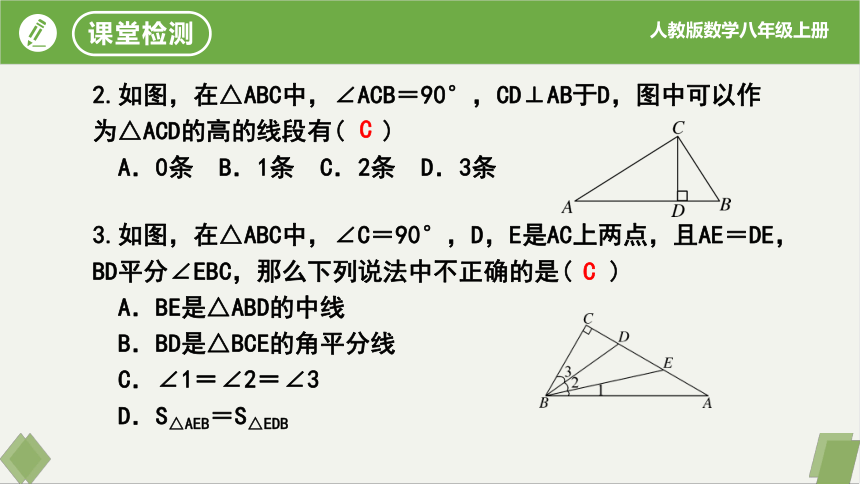
2.如图,在△ABC中,∠ACB=90°,CD⊥AB于D,图中可以作为△ACD的高的线段有( )
A.0条 B.1条 C.2条 D.3条
3.如图,在△ABC中,∠C=90°,D,E是AC上两点,且AE=DE,BD平分∠EBC,那么下列说法中不正确的是( )
A.BE是△ABD的中线
B.BD是△BCE的角平分线
C.∠1=∠2=∠3
D.S△AEB=S△EDB
C
C
解:若5cm为腰,设另外一边为xcm.
则:5+5+x=24,解得:x=14.
此时5+5<12,不能构成三角形;
若5cm为底边,设另外一边为xcm.
则:5+x+x=24,解得:x=9.5.
此时5+9.5>9.5,可以构成三角形.
4、等腰三角形的周长为24cm,一边长5cm,则另外一边长为 .
9.5cm
要利用三角形的
三边关系判断是否能构成三角形.
课堂检测
A.正五边形 B.三角形 C.平行四边形 D.长方形
5、下列具有稳定性的是( )
B
6、在△ABC中,AD是中线,若△ABC的面积为24,则△ABD的面积为 .
12
三角形的中线将三角形分成面积相等的两个小三角形.
解析:三角形具有稳定性.
课堂检测
知识点二与三角形有关的角
1、三角形的内角和定理
三角形三个内角的和等于180°.
2、直角三角形的性质
直角三角形的两个锐角互余.
有两个角互余的三角形是直角三角形.
知识梳理
3、三角形内角和定理的推论
三角形的外角等于与它不相邻的两个内角的和.
4、三角形外角和的性质
三角形的外角和等于360°.
知识点二与三角形有关的角
知识梳理
1、已知△ABC中,∠B=2(∠A+∠C),则∠B的度数是( )
A.90° B.100° C.120° D.135°
C
解:在△ABC中,∠A+∠B+∠C=180°.
∵∠B=2(∠A+∠C),
∴∠A+2(∠A+∠C)+∠C=180°,即:3(∠A+∠C)=180°.
∴∠A+∠C=60°,则∠B=120°.
课堂检测
2、在△ABC中,AB⊥BC,则∠C的度数是50°,则∠A的度数是 .
40°
解:∵AB⊥BC, ∴∠A+∠C=90°.
∵∠C=50°, ∴∠A=40°.
3、在△ABC中,∠A=70°,∠B=40°,则∠ACD的度数是 .
A
B
C
D
110°
解:∵∠ACD是△ABC的外角,
∠A=70°,∠B=40°,
∴ ∠ACD=∠A+∠B=110°.
课堂检测
4.如图,AD平分∠BAC,∠EAD=∠EDA.
(1)求证:∠EAC=∠B;(2)若∠B=50°,∠CAD∶∠E=1∶3,求∠E的度数.
课堂检测
(1)证明:∵AD平分∠BAC,
∴∠CAD=∠BAD=0.5∠BAC.
∵∠EDA=∠B+∠BAD,
∠EAD=∠CAD+∠EAC,∠EDA=∠EAD,
∴∠EAC=∠B.
(2)由(1)可知∠EAC=∠B=50°.
设∠CAD=x,
则∠E=3x,∠EAD=∠ADE=x+50°,
∴50°+x+50°+x+3x=180°.
∴x=16°.
∴∠E=3x=48°.
4.如图,AD平分∠BAC,∠EAD=∠EDA.
(1)求证:∠EAC=∠B;(2)若∠B=50°,∠CAD∶∠E=1∶3,求∠E的度数.
课堂检测
知识点三多边形及其内角和
1、多边形和正多边形的定义
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
各个角都相等,各个边都相等的多边形叫做正多边形.
2、n边形的内角和
n边形的内角和等于(n-2)×180°.
3、多边形的外角和
多边形的外角和等于360°.
知识梳理
4、正多边形的每一个内角度数的表示
5、正多边形的每一个外角度数的表示
6、n边形的对角线
正多边形的各个内角相等,则每个内角的度数为 .
正多边形的各个内角相等,则各个外角相等,即为 .
从n边形的一个顶点出发有(n-3)条对角线,将n边形分成(n-2个三角形,n边形共有 条对角线.
知识点三多边形及其内角和
知识梳理
1、一个多边形的内角和是1080°,这个多边形的边数是( )
A.7 B.8 C.9 D.10
B
解:设边数为n,
多边形内角和为(n-2)×180°,则(n-2)×180 =1080°,
解得:n=8.
课堂检测
课堂检测
2、一个多边形少算一个内角,其余内角之和是1500°,则这个多边形的边数是( )
A.8 B.9 C.10 D.11
3、如图,已知正五边形ABCDE, BG平分∠ABC , DG平分正五边形的外角∠EDF,则∠G=( )
A.36° B.54° C.60° D.72°
D
B
4、已知一个多边形的内角和是外角和的4倍,求这个多边形的边数.
解:设这个多边形的边数为n.
∵内角和是外角和的3倍,
∴(n-2)×180°=360°×4,
解得:n=10,
∴这个多边形的边数为10.
课堂检测
解:当底边为8cm,腰为3cm时,
∵3+3<8, ∴不能构成三角形;
当底边为3cm,腰为8cm时,
∵3+8>8, ∴能构成三角形.
周长为3+8+8=19(cm).
1.等腰三角形的两边长分别为3cm,8cm,则它的周长为( )
A.11cm B.19cm
C.11cm或14cm D.14cm或19cm
B
拓展训练
解:∵a,b,c为△ABC的三条边,
∴a+b>c,c-a0,a-b-c<0.
∴∣a+b-c∣+∣c-a-b∣=(a+b-c)+(-a+b+c)
=2b.
2.已知a,b,c是△ABC的三条边,化简∣a+b-c∣+∣a-b-c∣的结果为( )
A.2a+2b-2c B.2b C.2c D.0
B
拓展训练
拓展训练
3.如图,△ABC中,BD平分∠ABC, ∠1=∠2, ∠3=∠C,求∠1的度数.
A
B
C
D
)
)
)
)
2
4
1
3
解:设∠1=x,根据题意得
∠2=x.因为∠3=∠1+ ∠2, ∠4=∠2,
所以∠3=2x, ∠4=x,
又因为∠3=∠C,所以∠C=2x.
在△ABC中,根据三角形内角和定理,
得x+2x+2x=180 °,
解得x=36°,
所以∠1=36 °.
拓展训练
4.如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数.
A
B
C
F
G
D
E
解:连接CD,由“8字型”模型图可知
∠FCD+∠GDC=∠F+∠G,
所以∠A+∠B+∠C+∠D+∠E+∠F+∠G=(5-2)×180°=540°.
谢谢聆听
第11章三角形复习与小结
人教版数学八年级上册
三角形
边
与三角形
有关的线段
三角形的内角和
三角形的外角和
多边形的内角和
多边形的外角和
中线
高
角平分线
知识梳理
知识点一与三角形有关的线段
1、三角形的三边关系
三角形两边之和大于第三边,三角形两边之差小于第三边.
2、三角形的高、中线、角平分线的定义
从三角形的一个顶点向它所对的边所在直线画垂线,顶点与垂足之间的线段叫做三角形的这条边上的高.
连接三角形的一个顶点和它所对的边的中点,所得线段叫做三角形这条边上的中线.
三角形一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.
知识梳理
3、三角形的重心
三角形的三条中线的交点叫做三角形的重心.
4、三角形的稳定性
三角形具有稳定性,四边形具有不稳定性.
知识点一与三角形有关的线段
知识梳理
1.下列各组线段能构成三角形的是( )
A.2cm,3cm,7cm B.5cm,3cm,10cm
C.3cm,4cm,7cm D.5cm,6cm,9cm
D
A.2+3<7,不能构成三角形.
B.5+3<10,不能构成三角形.
C.3+4=7,不能构成三角形.
D.5+6>9,可以构成三角形.
判断三条线段是否可以构成
三角形,只需根据“两条较短的线段之和大于第三条线段”判断即可.
课堂检测
课堂检测
2.如图,在△ABC中,∠ACB=90°,CD⊥AB于D,图中可以作为△ACD的高的线段有( )
A.0条 B.1条 C.2条 D.3条
3.如图,在△ABC中,∠C=90°,D,E是AC上两点,且AE=DE,BD平分∠EBC,那么下列说法中不正确的是( )
A.BE是△ABD的中线
B.BD是△BCE的角平分线
C.∠1=∠2=∠3
D.S△AEB=S△EDB
C
C
解:若5cm为腰,设另外一边为xcm.
则:5+5+x=24,解得:x=14.
此时5+5<12,不能构成三角形;
若5cm为底边,设另外一边为xcm.
则:5+x+x=24,解得:x=9.5.
此时5+9.5>9.5,可以构成三角形.
4、等腰三角形的周长为24cm,一边长5cm,则另外一边长为 .
9.5cm
要利用三角形的
三边关系判断是否能构成三角形.
课堂检测
A.正五边形 B.三角形 C.平行四边形 D.长方形
5、下列具有稳定性的是( )
B
6、在△ABC中,AD是中线,若△ABC的面积为24,则△ABD的面积为 .
12
三角形的中线将三角形分成面积相等的两个小三角形.
解析:三角形具有稳定性.
课堂检测
知识点二与三角形有关的角
1、三角形的内角和定理
三角形三个内角的和等于180°.
2、直角三角形的性质
直角三角形的两个锐角互余.
有两个角互余的三角形是直角三角形.
知识梳理
3、三角形内角和定理的推论
三角形的外角等于与它不相邻的两个内角的和.
4、三角形外角和的性质
三角形的外角和等于360°.
知识点二与三角形有关的角
知识梳理
1、已知△ABC中,∠B=2(∠A+∠C),则∠B的度数是( )
A.90° B.100° C.120° D.135°
C
解:在△ABC中,∠A+∠B+∠C=180°.
∵∠B=2(∠A+∠C),
∴∠A+2(∠A+∠C)+∠C=180°,即:3(∠A+∠C)=180°.
∴∠A+∠C=60°,则∠B=120°.
课堂检测
2、在△ABC中,AB⊥BC,则∠C的度数是50°,则∠A的度数是 .
40°
解:∵AB⊥BC, ∴∠A+∠C=90°.
∵∠C=50°, ∴∠A=40°.
3、在△ABC中,∠A=70°,∠B=40°,则∠ACD的度数是 .
A
B
C
D
110°
解:∵∠ACD是△ABC的外角,
∠A=70°,∠B=40°,
∴ ∠ACD=∠A+∠B=110°.
课堂检测
4.如图,AD平分∠BAC,∠EAD=∠EDA.
(1)求证:∠EAC=∠B;(2)若∠B=50°,∠CAD∶∠E=1∶3,求∠E的度数.
课堂检测
(1)证明:∵AD平分∠BAC,
∴∠CAD=∠BAD=0.5∠BAC.
∵∠EDA=∠B+∠BAD,
∠EAD=∠CAD+∠EAC,∠EDA=∠EAD,
∴∠EAC=∠B.
(2)由(1)可知∠EAC=∠B=50°.
设∠CAD=x,
则∠E=3x,∠EAD=∠ADE=x+50°,
∴50°+x+50°+x+3x=180°.
∴x=16°.
∴∠E=3x=48°.
4.如图,AD平分∠BAC,∠EAD=∠EDA.
(1)求证:∠EAC=∠B;(2)若∠B=50°,∠CAD∶∠E=1∶3,求∠E的度数.
课堂检测
知识点三多边形及其内角和
1、多边形和正多边形的定义
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
各个角都相等,各个边都相等的多边形叫做正多边形.
2、n边形的内角和
n边形的内角和等于(n-2)×180°.
3、多边形的外角和
多边形的外角和等于360°.
知识梳理
4、正多边形的每一个内角度数的表示
5、正多边形的每一个外角度数的表示
6、n边形的对角线
正多边形的各个内角相等,则每个内角的度数为 .
正多边形的各个内角相等,则各个外角相等,即为 .
从n边形的一个顶点出发有(n-3)条对角线,将n边形分成(n-2个三角形,n边形共有 条对角线.
知识点三多边形及其内角和
知识梳理
1、一个多边形的内角和是1080°,这个多边形的边数是( )
A.7 B.8 C.9 D.10
B
解:设边数为n,
多边形内角和为(n-2)×180°,则(n-2)×180 =1080°,
解得:n=8.
课堂检测
课堂检测
2、一个多边形少算一个内角,其余内角之和是1500°,则这个多边形的边数是( )
A.8 B.9 C.10 D.11
3、如图,已知正五边形ABCDE, BG平分∠ABC , DG平分正五边形的外角∠EDF,则∠G=( )
A.36° B.54° C.60° D.72°
D
B
4、已知一个多边形的内角和是外角和的4倍,求这个多边形的边数.
解:设这个多边形的边数为n.
∵内角和是外角和的3倍,
∴(n-2)×180°=360°×4,
解得:n=10,
∴这个多边形的边数为10.
课堂检测
解:当底边为8cm,腰为3cm时,
∵3+3<8, ∴不能构成三角形;
当底边为3cm,腰为8cm时,
∵3+8>8, ∴能构成三角形.
周长为3+8+8=19(cm).
1.等腰三角形的两边长分别为3cm,8cm,则它的周长为( )
A.11cm B.19cm
C.11cm或14cm D.14cm或19cm
B
拓展训练
解:∵a,b,c为△ABC的三条边,
∴a+b>c,c-a
∴∣a+b-c∣+∣c-a-b∣=(a+b-c)+(-a+b+c)
=2b.
2.已知a,b,c是△ABC的三条边,化简∣a+b-c∣+∣a-b-c∣的结果为( )
A.2a+2b-2c B.2b C.2c D.0
B
拓展训练
拓展训练
3.如图,△ABC中,BD平分∠ABC, ∠1=∠2, ∠3=∠C,求∠1的度数.
A
B
C
D
)
)
)
)
2
4
1
3
解:设∠1=x,根据题意得
∠2=x.因为∠3=∠1+ ∠2, ∠4=∠2,
所以∠3=2x, ∠4=x,
又因为∠3=∠C,所以∠C=2x.
在△ABC中,根据三角形内角和定理,
得x+2x+2x=180 °,
解得x=36°,
所以∠1=36 °.
拓展训练
4.如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数.
A
B
C
F
G
D
E
解:连接CD,由“8字型”模型图可知
∠FCD+∠GDC=∠F+∠G,
所以∠A+∠B+∠C+∠D+∠E+∠F+∠G=(5-2)×180°=540°.
谢谢聆听
