辽宁省大连市第三中学2015届高三上学期第一次月考数学(文)试题(无答案)
文档属性
| 名称 | 辽宁省大连市第三中学2015届高三上学期第一次月考数学(文)试题(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 113.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-23 16:41:41 | ||
图片预览

文档简介
大连市第三中学2015届高三上学期第一次月考
数学文试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷 选择题 (共60分)
一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.已知全集,集合,,则结合=( )
A. B. C. D.
2.已知平面向量=(1,2),(m,4),且∥,则·=( )
A.4 B.-6 C.-10 D.10
3.已知幂函数的图象经过点,那么的解析式为( )
A. B.
C. D.
4.将函数的图象向左平移个单位, 再向上平移1个单位,所得图象的函数解析式是( ).
A. B. C. D.
5.关于直线,及平面α,β,下列命题中正确的是 ( )
A.若l∥α,αβ=m,则l∥m
B.若∥α,m∥α,则∥m
C.若l⊥α,l∥β,则α⊥β
D.若l∥α,m⊥l,则m⊥α
6.有四个关于三角函数的命题:
:xR, += : x、yR, sin(x-y)=sinx-siny
: x,=sinx : sinx=cosyx+y=
其中假命题的是( )
A ., B., C., D.,
7. 设成等比数列,其公比为2,则的值为( )
A. B. C. D.1
8.已知两点,,若直线上存在点满足,则实数的取值范围是( )
A. B.
C. D.
9. 一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积是( )
(A)
(B)
(C)
(D)
10. 已知函数定义域为,对于任意,都有.且时,,则( )
A.是偶函数且在上单调递减 B.是偶函数且在上单调递增
C. 是奇函数且在上单调递增 D.是奇函数且在上单调递减
11.具有性质:的函数,我们称为满足“倒负”变换的函数,下列函数:
①;②;③中满足“倒负”的函数是( )
A.①③ B.②③ C.①② D.只有①
12.已知二次函数,当n依次取时,其图像在x轴上所截得的线段的长度的总和为( )
A.1 B. C. D.
第II卷 客观题 (共90分)
二、填空:(本大题共4小题,每小题5分,满分20分)
13. 若函数,则的解集为 。
14. 已知锐角中,,,,则的面积为 。
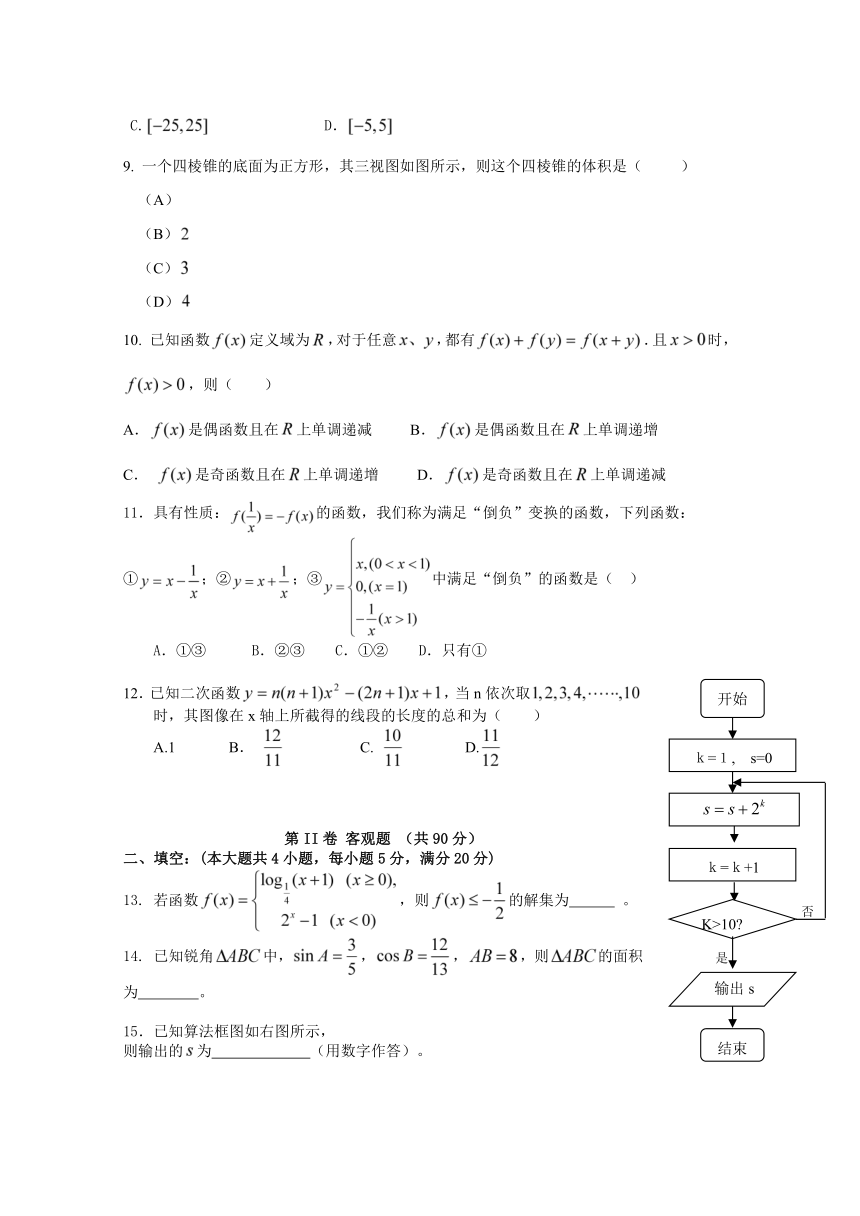
15.已知算法框图如右图所示,
则输出的为 (用数字作答)。
16. 已知数列满足,,则该数列的通项公式 。
三、解答题:本大题共6小题,满分60分.解答须写出文字说明,证明过程和演算步骤.
17.(本小题满分12分)
已知数列的前项和,数列为等比数列,且满足,
(1)求数列,的通项公式;
(2)求数列的前项和。
18. (本小题满分12分)
已知向量a,b满足a,b,函数a·b.
(1)将化成的形式;
(2)求的单调递增区间
(3)若,求的值域
19. (本小题满分12分)
如图,已知三棱柱的侧棱与底面
垂直,,,分别是,
的中点.
(Ⅰ)证明:;
(Ⅱ)判断直线和平面的位置关系,并
加以证明.
20.(本小题满分12分)
设且≠1,函数.
(1)当时,求曲线在(3,)处切线方程;
(2)求函数的极值点。
21. (本小题满分12分)
在中,为锐角,角所对的边分别为,且
(I)求的值;
(II)若,求的值。
22. (本小题满分10分)
经过点且方向向量为的直线,
求原点O到直线的距离。
判断直线与曲线C: 是否相交?说明理由。如果相交,求出弦长。
数学文试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷 选择题 (共60分)
一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.已知全集,集合,,则结合=( )
A. B. C. D.
2.已知平面向量=(1,2),(m,4),且∥,则·=( )
A.4 B.-6 C.-10 D.10
3.已知幂函数的图象经过点,那么的解析式为( )
A. B.
C. D.
4.将函数的图象向左平移个单位, 再向上平移1个单位,所得图象的函数解析式是( ).
A. B. C. D.
5.关于直线,及平面α,β,下列命题中正确的是 ( )
A.若l∥α,αβ=m,则l∥m
B.若∥α,m∥α,则∥m
C.若l⊥α,l∥β,则α⊥β
D.若l∥α,m⊥l,则m⊥α
6.有四个关于三角函数的命题:
:xR, += : x、yR, sin(x-y)=sinx-siny
: x,=sinx : sinx=cosyx+y=
其中假命题的是( )
A ., B., C., D.,
7. 设成等比数列,其公比为2,则的值为( )
A. B. C. D.1
8.已知两点,,若直线上存在点满足,则实数的取值范围是( )
A. B.
C. D.
9. 一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积是( )
(A)
(B)
(C)
(D)
10. 已知函数定义域为,对于任意,都有.且时,,则( )
A.是偶函数且在上单调递减 B.是偶函数且在上单调递增
C. 是奇函数且在上单调递增 D.是奇函数且在上单调递减
11.具有性质:的函数,我们称为满足“倒负”变换的函数,下列函数:
①;②;③中满足“倒负”的函数是( )
A.①③ B.②③ C.①② D.只有①
12.已知二次函数,当n依次取时,其图像在x轴上所截得的线段的长度的总和为( )
A.1 B. C. D.
第II卷 客观题 (共90分)
二、填空:(本大题共4小题,每小题5分,满分20分)
13. 若函数,则的解集为 。
14. 已知锐角中,,,,则的面积为 。
15.已知算法框图如右图所示,
则输出的为 (用数字作答)。
16. 已知数列满足,,则该数列的通项公式 。
三、解答题:本大题共6小题,满分60分.解答须写出文字说明,证明过程和演算步骤.
17.(本小题满分12分)
已知数列的前项和,数列为等比数列,且满足,
(1)求数列,的通项公式;
(2)求数列的前项和。
18. (本小题满分12分)
已知向量a,b满足a,b,函数a·b.
(1)将化成的形式;
(2)求的单调递增区间
(3)若,求的值域
19. (本小题满分12分)
如图,已知三棱柱的侧棱与底面
垂直,,,分别是,
的中点.
(Ⅰ)证明:;
(Ⅱ)判断直线和平面的位置关系,并
加以证明.
20.(本小题满分12分)
设且≠1,函数.
(1)当时,求曲线在(3,)处切线方程;
(2)求函数的极值点。
21. (本小题满分12分)
在中,为锐角,角所对的边分别为,且
(I)求的值;
(II)若,求的值。
22. (本小题满分10分)
经过点且方向向量为的直线,
求原点O到直线的距离。
判断直线与曲线C: 是否相交?说明理由。如果相交,求出弦长。
同课章节目录
