九年级数学上册试题 4.6 利用相似三角形测高 同步练习-北师大版(含答案)
文档属性
| 名称 | 九年级数学上册试题 4.6 利用相似三角形测高 同步练习-北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 525.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-10 18:00:25 | ||
图片预览

文档简介
4.6 利用相似三角形测高
一、单选题
1.小华同学的身高为米,某一时刻他在阳光下的影长为米,与他邻近的一棵树的影长为米,则这棵树的高为( )
A.米 B.米 C.米 D.米
2.图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面( )
A. B.
C. D.
3.如图,树AB在路灯O的照射下形成投影AC,已知路灯高,树影,树AB与路灯O的水平距离,则树的高度AB长是( )
A. B. C. D.
4.小刚身高,测得他站立在阳光下的影子长为,紧接着他把手臂竖直举起,测得影子长为,那么小刚举起的手臂超出头顶( )
A. B. C. D.
5.如图,已知零件的外径,现用一个交叉卡钳(两条尺长和相等,)量零件的内孔直径,若,量的,则零件的厚度为( )
A. B. C. D.
6.如图,花丛中有一路灯杆AB.在灯光下,小明在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时小明的影长GH=5米.如果小明的身高为1.7米,则路灯杆AB的高度(精确到1米)为( )
A.5米 B.6米 C.7米 D.8米
7.如图,数学兴趣小组的小颖想测量教学楼前的一棵树的树高,下午课外活动时她测得一根长为1的竹竿的影长是0.6,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),他先测得留在墙壁上的影高为0.9,又测得地面的影长为2.7,请你帮她算一下,树高是( )
A.7 B.6 C.4.5 D.5.4
8.如图,李老师用自制的直角三角形纸板去测“步云图”的高度,他调整自己的位置,设法使斜边保持水平,并且边与点B在同一直线上.已知纸板的两条直角边,,测得眼睛D离地面的高度为,他与“步云图”的水平距离为,则“步云图”的高度是( )m.
A.75.5 B.77.1 C.79.8 D.82.5
9.《九章算术》中,有一数学史上有名的测量问题:“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”今译如下:如图,矩形,东边城墙长9里,南边城墙长7里,东门点,南门点分别位于,的中点,,,里,经过点,则的长为( )
A.0.95里 B.1.05里 C.2.05里 D.2.15里
10.如图是一块三角形钢材ABC,其中边,高,把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,则这个正方形零件的边长是( )
A.16 B.24 C.30 D.36
11.如图,为了测量校园水平地面上一棵树的高度,数学兴趣小组做了如下的探索:把一面很小的镜子水平放置在离树底()7.8米的点处,然后观察者沿着直线后退到点,这时恰好在镜子里看到树梢顶点,再用皮尺量得米,观察者目高米,则树()的高度约为( )米.
A.15.6 B.6.4 C.3.4 D.3.9
二、填空题
12.如图,为了测量山坡的护坡石坝高,把一根长为的竹竿斜靠在石坝旁,量出竿上长为时,它离地面的高度为,则坝高为__________.
13.《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆,从木杆的顶端D观察水岸C,视线与井口的直径交于点E,如果测得米,米,米,那么井深为______米.
14.平行于墙面的三角尺在灯泡O的照射下在墙上形成的影子如图所示.若,,则三角尺与它在墙上影子的周长比是________.
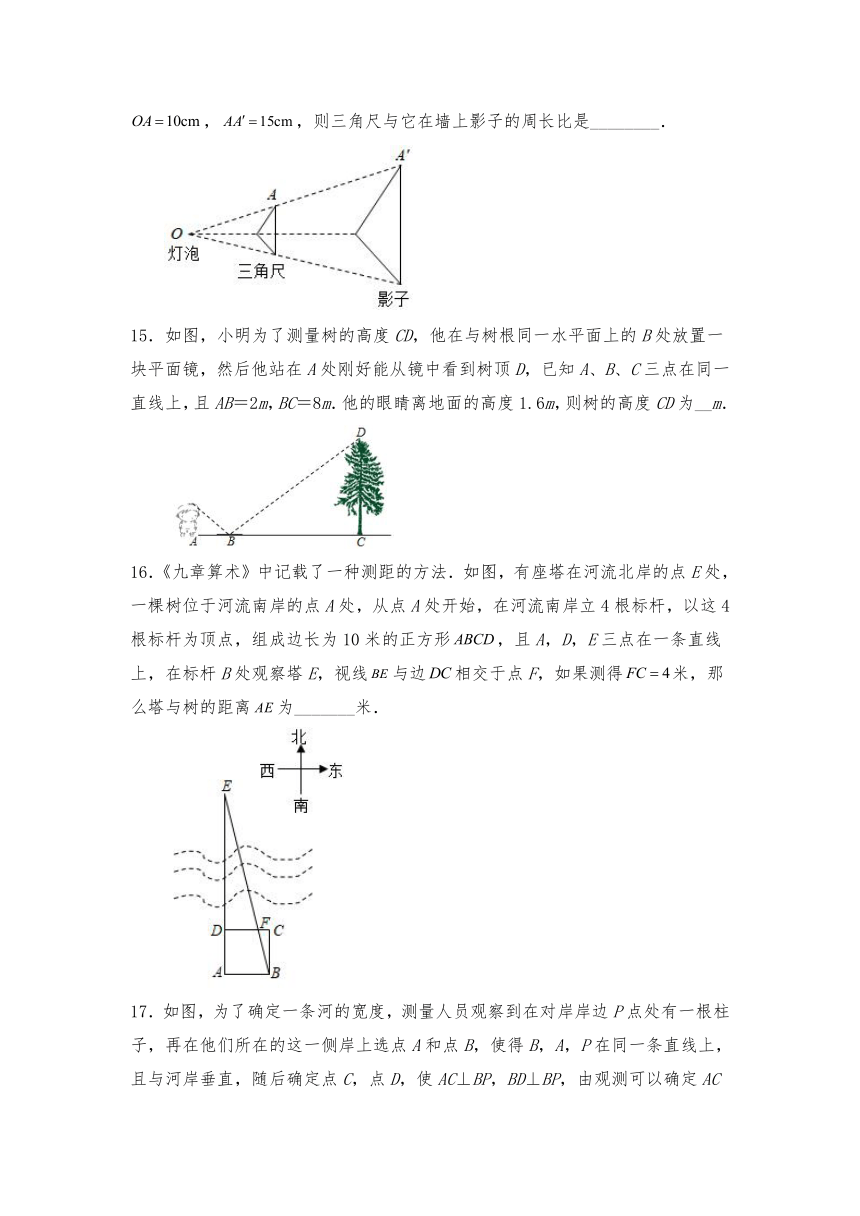
15.如图,小明为了测量树的高度CD,他在与树根同一水平面上的B处放置一块平面镜,然后他站在A处刚好能从镜中看到树顶D,已知A、B、C三点在同一直线上,且AB=2m,BC=8m.他的眼睛离地面的高度1.6m,则树的高度CD为__m.
16.《九章算术》中记载了一种测距的方法.如图,有座塔在河流北岸的点E处,一棵树位于河流南岸的点A处,从点A处开始,在河流南岸立4根标杆,以这4根标杆为顶点,组成边长为10米的正方形,且A,D,E三点在一条直线上,在标杆B处观察塔E,视线与边相交于点F,如果测得米,那么塔与树的距离为_______米.
17.如图,为了确定一条河的宽度,测量人员观察到在对岸岸边P点处有一根柱子,再在他们所在的这一侧岸上选点A和点B,使得B,A,P在同一条直线上,且与河岸垂直,随后确定点C,点D,使AC⊥BP,BD⊥BP,由观测可以确定AC与DP的交点C.他们测得AB=20m,AC=40m,BD=50m,从而确定河宽PA为_____m.
18.如图,小树AB在路灯O的照射下形成投影BC.若树高AB=2m,树影BC=3m,树与路灯的水平距离BP=4m.则路灯的高度OP为_____m.
19.如图,铁路道口的栏杆短臂长,长臂长.当短臂端点下降时,长臂端点升高(杆的宽度忽略不计)的长度为__________.
20.《孙子算经》中有道歌谣算术题:“今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺六寸,影长四寸.问竿长几何?”歌谣的意思是:有一根竹竿不知道它的长度,量出它在太阳下的影子长一丈五尺.同时立一根一尺六寸的小标杆,它的影长四寸,则竹竿的长度是____________.(注意:1丈=10尺,1尺=10寸)
21.如图,小明用相似图形的知识测量旗杆高度,已知小明的眼睛离地面1.5米,他将3米长的标杆竖直放置在身前3米处,此时小明的眼睛、标杆的顶端、旗杆的顶端在一条直线上,通过计算测得旗杆高度为15米,则旗杆和标杆之间距离CE长___________米.
22.如图,一条河的两岸有一段是平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔60米有一根电线杆.丁丁站在离南岸边15米的点A处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为____米.
三、解答题
23.一天上午课间活动,小明与同学合作利用太阳光线测量旗杆的高度,身高1.6m的小明落在地面上的影长BC=2.5m.
(1)请你在图中画出旗杆在同一时刻太阳光照射下落在地面上的影子EF,并简要的写出画法;
(2)若小明测得此刻旗杆落在地面的影长EF=15m,请求出旗杆DE的高度.
24.如图,马路上有一路灯O,小明沿着散步,当他在距路灯灯柱6米远的B处时,他在地面上的影长是3米,问当他在距路灯灯柱10米远的D处时,他的影长是多少米?
25.九年级活动小组计划利用所学的知识测量操场旗杆高度.测量方案如下:如图,小卓在小越和旗杆之间的直线BM上平放一平面镜,在镜面上做了一个标记,这个标记在直线BM上的对应位置为点C,镜子不动,小卓看着镜面上的标记,他来回走动,走到点D时看到旗杆顶端点A在镜面中的像与镜面上的标记点C重合,这时测得小卓眼睛与地面的高度ED=1.5米,CD=1米,然后在阳光下,小越从D点沿DM方向走了15.8米到达F处此时旗杆的影子顶端与小越的影子顶端恰好重合,测得FG=1.6米,FH=3.2米,已知AB⊥BM,ED⊥BM,GF⊥BM若测量时所使用的平面镜的厚度忽略不计,请你根据图中提供的相关信息求出旗杆的高AB.
26.小刚和小亮想用测量工具和几何知识测量公园古树的高度,由于有围栏保护,他们无法到达底部,如图,围栏米,小刚在延长线点放一平面镜,镜子不动,当小刚走到点时,恰好可以通过镜子看到树顶,这时小刚眼睛与地面的高度米,米,米;同时,小亮在的延长线上的处安装了测倾器(测倾器的高度忽略不计),测得树顶的仰角,米,请根据题中提供的相关信息,求出古树的高度.
27.如图,某校数学兴趣小组利用自制的直角三角形硬纸板来测量操场旗杆的高度,他们通过调整测量位置,使斜边与地面保持平行并使直角边与旗杆顶点在同一直线上,已知米,米,且测点到地面的距离米,,到旗杆的水平距离米,求旗杆的高度.
28.如图是一个铁夹子的侧面示意图,点是连接夹面的轴上一点,于点.这个侧面图是轴对称图形,直线是它的对称轴.已知,,.求点与点之间的距离.
答案
一、单选题
B.C.A.B.B.B.D.C.B.B.D.
二、填空题
12.2.7
13.7
14.
15.6.4
16.25
17.80
18.
19.
20.六丈
21.24
22.30
三、解答题
23.解:(1)影子EF如图所示.连接AC,过D点作DF∥AC交BC于F点,则EF为所求.
(2)∵DF∥AC,
∴∠DFE=∠ACB,
∵∠DEF=∠ABC=90°
∴Rt△ABC∽△Rt△DEF,
∴,
又∵AB=1.6m ,BC=2.5m, EF=15m
∴m
∴旗杆的高度为9.6m.
24.解:设小明身高为米,即米,
灯柱高米,由题,,则,
∵∠ABE=∠OPE=90°,∠AEB=∠OEP,
∴,
∴,即,
∵∠CDF=∠OPE=90°,∠CFD=∠OEP,
∴,
设DF=x,
则,即,
,
解得:.
当小明距路灯柱10米时,他的影长为5米.
25.解:由题意可得:∠BCA=∠ECD,∠ABC=∠EDC,
故△ABC∽△EDC,
则,
即=1.5,
∴AB=1.5BC,
∵GF∥AB,
∴△GFH∽△ABH,
∴,
∴,
解得:BC=10,
经检验,BC=10是上述分式方程的解且符合实际意义,
故AB=1.5BC=15米.
答:旗杆的高AB为15米.
26.设古树AB的高度为x米,
∵,米,
∴米,
∴米,
∴米,
由题意可知,在和中,
∴,
∴,即,
解得:.
故古树AB的高度为15米.
27.解:∵,,
∴,
∵,米,
∴四边形CBGD是矩形,
∴,
∵∠ADC=∠ADC,,
∴,
∴,
∵米,米,米,
∴,
∴米,
∴.
28.连接AB交直线OC于点E,
根据轴对称图形的性质得直线OC⊥AB,AE=BE,
,
,
∴,
∴,即,
∴,
∴.
答:点与点之间的距离为.
一、单选题
1.小华同学的身高为米,某一时刻他在阳光下的影长为米,与他邻近的一棵树的影长为米,则这棵树的高为( )
A.米 B.米 C.米 D.米
2.图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面( )
A. B.
C. D.
3.如图,树AB在路灯O的照射下形成投影AC,已知路灯高,树影,树AB与路灯O的水平距离,则树的高度AB长是( )
A. B. C. D.
4.小刚身高,测得他站立在阳光下的影子长为,紧接着他把手臂竖直举起,测得影子长为,那么小刚举起的手臂超出头顶( )
A. B. C. D.
5.如图,已知零件的外径,现用一个交叉卡钳(两条尺长和相等,)量零件的内孔直径,若,量的,则零件的厚度为( )
A. B. C. D.
6.如图,花丛中有一路灯杆AB.在灯光下,小明在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时小明的影长GH=5米.如果小明的身高为1.7米,则路灯杆AB的高度(精确到1米)为( )
A.5米 B.6米 C.7米 D.8米
7.如图,数学兴趣小组的小颖想测量教学楼前的一棵树的树高,下午课外活动时她测得一根长为1的竹竿的影长是0.6,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),他先测得留在墙壁上的影高为0.9,又测得地面的影长为2.7,请你帮她算一下,树高是( )
A.7 B.6 C.4.5 D.5.4
8.如图,李老师用自制的直角三角形纸板去测“步云图”的高度,他调整自己的位置,设法使斜边保持水平,并且边与点B在同一直线上.已知纸板的两条直角边,,测得眼睛D离地面的高度为,他与“步云图”的水平距离为,则“步云图”的高度是( )m.
A.75.5 B.77.1 C.79.8 D.82.5
9.《九章算术》中,有一数学史上有名的测量问题:“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”今译如下:如图,矩形,东边城墙长9里,南边城墙长7里,东门点,南门点分别位于,的中点,,,里,经过点,则的长为( )
A.0.95里 B.1.05里 C.2.05里 D.2.15里
10.如图是一块三角形钢材ABC,其中边,高,把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,则这个正方形零件的边长是( )
A.16 B.24 C.30 D.36
11.如图,为了测量校园水平地面上一棵树的高度,数学兴趣小组做了如下的探索:把一面很小的镜子水平放置在离树底()7.8米的点处,然后观察者沿着直线后退到点,这时恰好在镜子里看到树梢顶点,再用皮尺量得米,观察者目高米,则树()的高度约为( )米.
A.15.6 B.6.4 C.3.4 D.3.9
二、填空题
12.如图,为了测量山坡的护坡石坝高,把一根长为的竹竿斜靠在石坝旁,量出竿上长为时,它离地面的高度为,则坝高为__________.
13.《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆,从木杆的顶端D观察水岸C,视线与井口的直径交于点E,如果测得米,米,米,那么井深为______米.
14.平行于墙面的三角尺在灯泡O的照射下在墙上形成的影子如图所示.若,,则三角尺与它在墙上影子的周长比是________.
15.如图,小明为了测量树的高度CD,他在与树根同一水平面上的B处放置一块平面镜,然后他站在A处刚好能从镜中看到树顶D,已知A、B、C三点在同一直线上,且AB=2m,BC=8m.他的眼睛离地面的高度1.6m,则树的高度CD为__m.
16.《九章算术》中记载了一种测距的方法.如图,有座塔在河流北岸的点E处,一棵树位于河流南岸的点A处,从点A处开始,在河流南岸立4根标杆,以这4根标杆为顶点,组成边长为10米的正方形,且A,D,E三点在一条直线上,在标杆B处观察塔E,视线与边相交于点F,如果测得米,那么塔与树的距离为_______米.
17.如图,为了确定一条河的宽度,测量人员观察到在对岸岸边P点处有一根柱子,再在他们所在的这一侧岸上选点A和点B,使得B,A,P在同一条直线上,且与河岸垂直,随后确定点C,点D,使AC⊥BP,BD⊥BP,由观测可以确定AC与DP的交点C.他们测得AB=20m,AC=40m,BD=50m,从而确定河宽PA为_____m.
18.如图,小树AB在路灯O的照射下形成投影BC.若树高AB=2m,树影BC=3m,树与路灯的水平距离BP=4m.则路灯的高度OP为_____m.
19.如图,铁路道口的栏杆短臂长,长臂长.当短臂端点下降时,长臂端点升高(杆的宽度忽略不计)的长度为__________.
20.《孙子算经》中有道歌谣算术题:“今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺六寸,影长四寸.问竿长几何?”歌谣的意思是:有一根竹竿不知道它的长度,量出它在太阳下的影子长一丈五尺.同时立一根一尺六寸的小标杆,它的影长四寸,则竹竿的长度是____________.(注意:1丈=10尺,1尺=10寸)
21.如图,小明用相似图形的知识测量旗杆高度,已知小明的眼睛离地面1.5米,他将3米长的标杆竖直放置在身前3米处,此时小明的眼睛、标杆的顶端、旗杆的顶端在一条直线上,通过计算测得旗杆高度为15米,则旗杆和标杆之间距离CE长___________米.
22.如图,一条河的两岸有一段是平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔60米有一根电线杆.丁丁站在离南岸边15米的点A处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为____米.
三、解答题
23.一天上午课间活动,小明与同学合作利用太阳光线测量旗杆的高度,身高1.6m的小明落在地面上的影长BC=2.5m.
(1)请你在图中画出旗杆在同一时刻太阳光照射下落在地面上的影子EF,并简要的写出画法;
(2)若小明测得此刻旗杆落在地面的影长EF=15m,请求出旗杆DE的高度.
24.如图,马路上有一路灯O,小明沿着散步,当他在距路灯灯柱6米远的B处时,他在地面上的影长是3米,问当他在距路灯灯柱10米远的D处时,他的影长是多少米?
25.九年级活动小组计划利用所学的知识测量操场旗杆高度.测量方案如下:如图,小卓在小越和旗杆之间的直线BM上平放一平面镜,在镜面上做了一个标记,这个标记在直线BM上的对应位置为点C,镜子不动,小卓看着镜面上的标记,他来回走动,走到点D时看到旗杆顶端点A在镜面中的像与镜面上的标记点C重合,这时测得小卓眼睛与地面的高度ED=1.5米,CD=1米,然后在阳光下,小越从D点沿DM方向走了15.8米到达F处此时旗杆的影子顶端与小越的影子顶端恰好重合,测得FG=1.6米,FH=3.2米,已知AB⊥BM,ED⊥BM,GF⊥BM若测量时所使用的平面镜的厚度忽略不计,请你根据图中提供的相关信息求出旗杆的高AB.
26.小刚和小亮想用测量工具和几何知识测量公园古树的高度,由于有围栏保护,他们无法到达底部,如图,围栏米,小刚在延长线点放一平面镜,镜子不动,当小刚走到点时,恰好可以通过镜子看到树顶,这时小刚眼睛与地面的高度米,米,米;同时,小亮在的延长线上的处安装了测倾器(测倾器的高度忽略不计),测得树顶的仰角,米,请根据题中提供的相关信息,求出古树的高度.
27.如图,某校数学兴趣小组利用自制的直角三角形硬纸板来测量操场旗杆的高度,他们通过调整测量位置,使斜边与地面保持平行并使直角边与旗杆顶点在同一直线上,已知米,米,且测点到地面的距离米,,到旗杆的水平距离米,求旗杆的高度.
28.如图是一个铁夹子的侧面示意图,点是连接夹面的轴上一点,于点.这个侧面图是轴对称图形,直线是它的对称轴.已知,,.求点与点之间的距离.
答案
一、单选题
B.C.A.B.B.B.D.C.B.B.D.
二、填空题
12.2.7
13.7
14.
15.6.4
16.25
17.80
18.
19.
20.六丈
21.24
22.30
三、解答题
23.解:(1)影子EF如图所示.连接AC,过D点作DF∥AC交BC于F点,则EF为所求.
(2)∵DF∥AC,
∴∠DFE=∠ACB,
∵∠DEF=∠ABC=90°
∴Rt△ABC∽△Rt△DEF,
∴,
又∵AB=1.6m ,BC=2.5m, EF=15m
∴m
∴旗杆的高度为9.6m.
24.解:设小明身高为米,即米,
灯柱高米,由题,,则,
∵∠ABE=∠OPE=90°,∠AEB=∠OEP,
∴,
∴,即,
∵∠CDF=∠OPE=90°,∠CFD=∠OEP,
∴,
设DF=x,
则,即,
,
解得:.
当小明距路灯柱10米时,他的影长为5米.
25.解:由题意可得:∠BCA=∠ECD,∠ABC=∠EDC,
故△ABC∽△EDC,
则,
即=1.5,
∴AB=1.5BC,
∵GF∥AB,
∴△GFH∽△ABH,
∴,
∴,
解得:BC=10,
经检验,BC=10是上述分式方程的解且符合实际意义,
故AB=1.5BC=15米.
答:旗杆的高AB为15米.
26.设古树AB的高度为x米,
∵,米,
∴米,
∴米,
∴米,
由题意可知,在和中,
∴,
∴,即,
解得:.
故古树AB的高度为15米.
27.解:∵,,
∴,
∵,米,
∴四边形CBGD是矩形,
∴,
∵∠ADC=∠ADC,,
∴,
∴,
∵米,米,米,
∴,
∴米,
∴.
28.连接AB交直线OC于点E,
根据轴对称图形的性质得直线OC⊥AB,AE=BE,
,
,
∴,
∴,即,
∴,
∴.
答:点与点之间的距离为.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
