九年级数学上册试题 一课一练1.3 正方形的性质与判定--北师大版(含答案)
文档属性
| 名称 | 九年级数学上册试题 一课一练1.3 正方形的性质与判定--北师大版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 619.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-10 00:00:00 | ||
图片预览




文档简介
1.3 正方形的性质与判定
一、单选题
1.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的条件是( )
A.AC=BD,AB∥CD,AB=CD B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD D.AO=CO,BO=DO,AB=BC
2.如图,是正方形的边上的一个动点,的垂直平分线交对角线于点,交于点,连接,,则的度数是( )
A.45° B.50° C.60° D.不确定
3.已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE,过点A作AE的垂线交DE于点P,若AE=AP=1,PB=.下列结论:①△APD≌△AEB;②点B到直线AE的距离为;③EB⊥ED;④S△APD+S△APB=1+;⑤S正方形ABCD=4+.其中正确结论的序号是( )
A.①③④ B.①②⑤ C.③④⑤ D.①③⑤
4.如图,过正方形的顶点作直线,点、到直线的距离分别为和,则的长为( )
A. B. C. D.
5.如图,在边长为4的正方形ABCD中,点E、F分别是边BC、CD上的动点,且BE=CF,连接BF、DE,则BF+DE的最小值为()
A. B. C. D.
6.如图,点P是边长为2cm的正方形ABCD的边上一动点,O是对角线的交点,当点P由A→D→C运动时,设DP=xcm,则△POD的面积y(cm2)随x(cm)变化的关系图象为( )
A. B.
C. D.
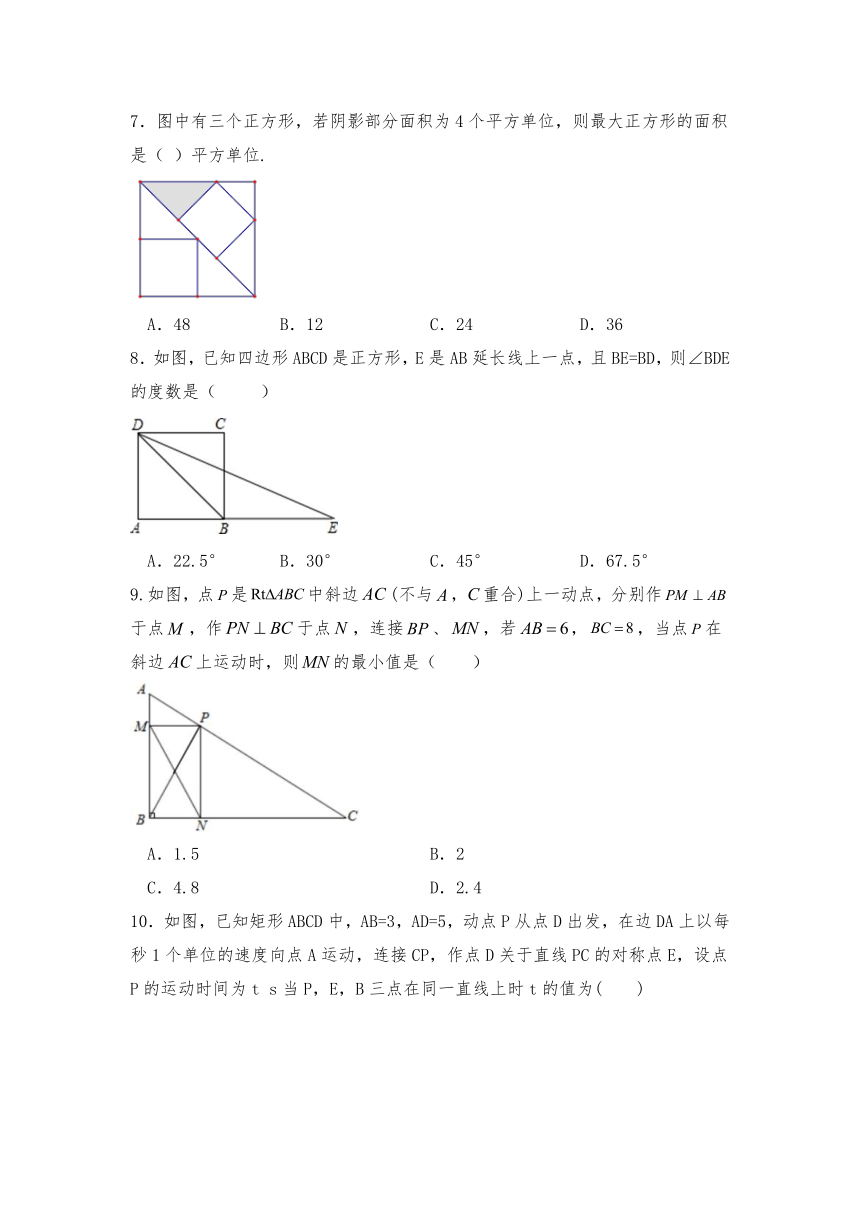
7.图中有三个正方形,若阴影部分面积为4个平方单位,则最大正方形的面积是( )平方单位.
A.48 B.12 C.24 D.36
8.如图,已知四边形ABCD是正方形,E是AB延长线上一点,且BE=BD,则∠BDE的度数是( )
A.22.5° B.30° C.45° D.67.5°
9.如图,点是中斜边(不与,重合)上一动点,分别作于点,作于点,连接、,若,,当点在斜边上运动时,则的最小值是( )
A.1.5 B.2
C.4.8 D.2.4
10.如图,已知矩形ABCD中,AB=3,AD=5,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t s当P,E,B三点在同一直线上时t的值为( )
A.1 B.4 C. D.2
11.如图,四边形ABCD的对角线相交于点O,且点O是BD的中点,若AB=AD=5,BD=8,∠ABD=∠CDB,则四边形ABCD的面积为( )
A.40 B.24 C.20 D.15
12.如图,在菱形中,已知,,,点在的延长线上,点在的延长线上,有下列结论:①;②;③;④若,则点到的距离为.则其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
13.如图,四边形ABCD中,∠ABC=∠BCD=∠CDA=90°,请添加一个条件_____,可得出该四边形是正方形.
14.如图,点E为正方形ABCD边CB延长线上一点,点F为AB上一点,连接AE,CF,AC,若BE=BF,∠E=70°,则∠ACF=_____.
15.如图,在矩形纸片ABCD中,AB=4,BC=4,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A'EF,连接A'C,A'D,则当△A'DC是以A'D为腰的等腰三角形时,FD的长是_____.
16.如图,直线l过正方形ABCD的顶点A,点B、D到直线l的距离分别为1、3,则正方形的边长为_______.
17.如图,在菱形中,,,点,同时由,两点出发,分别沿,方向向点匀速运动,点的运动速度为,点的运动速度为,点到达点后,点与点同时停止运动.若运动时间为秒时,为等边三角形,则的值为__________.
18.如图,在菱形c中,分别是边,对角线与边上的动点,连接,若,则的最小值是___.
19.如图,四边形ACDF是正方形,和都是直角,且点三点共线,,则阴影部分的面积是__________.
20.如图,四边形ABCD中,∠A=90°,AB=3,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为 .
三、解答题
21.已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形.
22.如图,△ABC 中,点 O 是边 AC 上一个动点,过 O 作直线 MN∥BC,设 MN 交∠ACB 的平分线于点 E,交∠ACB 的外角平分线于点 F.
(1)求证:OE=OF;
(2)当点 O 在边 AC 上运动到什么位置时,四边形 AECF 是矩形?并说明理由.
(3)若 AC 边上存在点 O,使四边形 AECF 是正方形,猜想△ABC 的形状并证明你的结论.
23.如图1,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形ABCD的外角∠DCG的平分线CF于点F.
(1)如图2,取AB的中点H,连接HE,求证:AE=EF.
(2)如图3,若点E是BC的延长线上(除C点外)的任意一点,其他条件不变结论“AE=EF”仍然成立吗?如果正确,写出证明过程:如果不正确,请说明理由.
24.已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.
(1)求证:△BGF≌△FHC;
(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.
25.如图,矩形ABCD 和正方形ECGF,其中E、H分别为AD、BC中点,连结AF、HG、AH.
(1)求证:;
(2)求证:;
26.如图,E、F、 G、H分别为四边形ABCD四边之中点.
(1)求证:四边形EFGH为平行四边形;
(2)当AC、BD满足______时,四边形EFGH为矩形.
27.如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,得到A,B的对应点C,D,连接AC,BD,CD.
(1)直接写出点C,D的坐标,求出四边形ABDC的面积;
(2)在x轴上是否存在一点F,使得三角形DFC的面积是三角形DFB面积的2倍,若存在,请求出点F的坐标;若不存在,请说明理由.
28.如图,在菱形ABCD中,点E是BC边的中点,动点M在CD边上运动,以EM为折痕将△CEM折叠得到△PEM,连接PA,若AB=4,∠BAD=60°, 求PA的最小值是.
29.如图,在正方形ABCD中,E是边AB上的一动点(不与点A、B重合),连接DE,点A关于直线DE的对称点为F,连接EF并延长交BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H,连接BH.
(1)求证:GF=GC;
(2)用等式表示线段BH与AE的数量关系,并证明.
答案
一、单选题
C.A.D.A. D.B.D.A.C.A.B.B.
二、填空题
13.AB=BC.
14.25°.
15.4-2或3.
16..
17..
18..
19.8.
20.3.
三、解答题
21.(1)在△ADE与△CDE中,
,
∴△ADE≌△CDE,
∴∠ADE=∠CDE,
∵AD∥BC,
∴∠ADE=∠CBD,
∴∠CDE=∠CBD,
∴BC=CD,
∵AD=CD,
∴BC=AD,
∴四边形ABCD为平行四边形,
∵AD=CD,
∴四边形ABCD是菱形;
(2)∵BE=BC,
∴∠BCE=∠BEC,
∵∠CBE:∠BCE=2:3,
∴∠CBE=180× =45°,
∵四边形ABCD是菱形,
∴∠ABE=45°,
∴∠ABC=90°,
∴四边形ABCD是正方形.
22.证明:(1)∵MN 交∠ACB 的平分线于点 E,交∠ACB 的外角平分线于点 F,
∴∠2=∠5,∠4=∠6,
∵MN∥BC,
∴∠1=∠5,∠3=∠6,
∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,
∴OE=OF;
(2)当点 O 在边 AC 上运动到 AC 中点时,四边形 AECF 是矩形.
证明:当 O 为 AC 的中点时,AO=CO,
∵EO=FO,
∴四边形 AECF 是平行四边形,
∵CE是∠ACB 的平分线,CF是∠ACD的平分线,
∴∠ECF= (∠ACB +∠ACD)=90°,
∴平行四边形 AECF 是矩形.
(3)△ABC 是直角三角形,
理由:∵四边形 AECF 是正方形,
∴AC⊥EN,故∠AOM=90°,
∵MN∥BC,
∴∠BCA=∠AOM,
∴∠BCA=90°,
∴△ABC 是直角三角形.
23.(1)证明:取AB的中点H,连接EH;如图1所示
∵四边形ABCD是正方形,AE⊥EF;
∴∠1+∠AEB=90°,∠2+∠AEB=90°
∴∠1=∠2,
∵BH=BE,∠BHE=45°,且∠FCG=45°,
∴∠AHE=∠ECF=135°,AH=CE,
在△AHE和△ECF中,
,
∴△AHE≌△ECF(ASA),
∴AE=EF;
(2)解:AE=EF成立,
理由如下:如图2,延长BA到M,使AM=CE,
∵∠AEF=90°,
∴∠FEG+∠AEB=90°.
∵∠BAE+∠AEB=90°,
∴∠BAE=∠FEG,
∴∠MAE=∠CEF.
∵AB=BC,
∴AB+AM=BC+CE,
即BM=BE.
∴∠M=45°,
∴∠M=∠FCE.
在△AME与△ECF中,
,
∴△AME≌△ECF(ASA),
∴AE=EF.
24.(1)连接EF,∵点F,G,H分别是BC,BE,CE的中点,
∴FH∥BE,FH=BE,FH=BG,
∴∠CFH=∠CBG,
∵BF=CF,
∴△BGF≌△FHC,
(2)当四边形EGFH是正方形时,连接GH,可得:EF⊥GH且EF=GH,
∵在△BEC中,点G,H分别是BE,CE的中点,
∴ 且GH∥BC,
∴EF⊥BC,
∵AD∥BC,AB⊥BC,
∴AB=EF=GH=a,
∴矩形ABCD的面积=
25.(1)证明:∵四边形ABCD是矩形,且E、H分别为AD、BC的中点,
∴,,
∴四边形AHCE为平行四边形,
∴,,
又∵四边形ECGF为正方形,
∴,,
∴,,
∴四边形AHGF是平行四边形,
∴;
(2)证明:∵四边形AHGF是平行四边形,
∴,
∵四边形ABCD是矩形,
∴,
∴,
又∵,
∴;
26.(1)证明:连接BD
∵E、F、 G、H分别为四边形ABCD四边的中点
∴EH是△ABD的中位线,FG是△CBD的中位线
∴EH∥BD,EH=,FG∥BD,FG=
∴EH∥FG,EH= FG
∴四边形EFGH为平行四边形;
(2)当AC⊥BD时,四边形EFGH为矩形,理由如下
连接AC,
∵E、F为BA和BC的中点
∴EF为△BAC的中位线
∴EF∥AC
∵AC⊥BD
∴EF⊥BD
∵EH∥BD
∴EF⊥EH
∴∠FEH=90°
∵四边形EFGH为平行四边形
∴四边形EFGH为矩形
故答案为:AC⊥BD.
27.(1)依题意可得C(0,2),D(4,2).S四边形ABDC=AB·OC=4×2=8.
(2)存在,
当BF=CD时,三角形DFC的面积是三角形DFB面积的2倍.
∵C(0,2),D(4,2),
∴CD=4,BF=CD=2.
∵B(3,0),
∴F(1,0)或(5,0).
28.解:根据折叠的性质得,EP=CE=BC=2,
故点P在以E为圆心,EP为半径的半圆上,
∵AP+EP≥AE,
∴当A,P,E在同一直线上时,AP最短,
如图,过点E作EF⊥AB于点F,
∵在边长为4的菱形ABCD中,∠BAD=60°,E为BC的中点,
∴BE=BC=2,∠EBF=60°,
∴∠BEF=30°,
∴BF=BE=1,
∴,AF=5,
∴
∴PA的最小值=AE﹣PE=.
故答案为:.
29.(1)证明:连接.
∵,关于对称.
∴..
在和中.
∴
∴.
∵四边形是正方形
∴.
∴
∴
∴
∵.
∴
在和.
∴≌
∴.
(2).
证明:在上取点使得,连接.
∵四这形是正方形.
∴..
∵≌
∴
同理:
∴
∵
∴
∴
∴
∴.
∵
∴
∵
∴
∴
∵.
∴
在和中
∴≌
∴
在中,,.
∴
∴.
一、单选题
1.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的条件是( )
A.AC=BD,AB∥CD,AB=CD B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD D.AO=CO,BO=DO,AB=BC
2.如图,是正方形的边上的一个动点,的垂直平分线交对角线于点,交于点,连接,,则的度数是( )
A.45° B.50° C.60° D.不确定
3.已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE,过点A作AE的垂线交DE于点P,若AE=AP=1,PB=.下列结论:①△APD≌△AEB;②点B到直线AE的距离为;③EB⊥ED;④S△APD+S△APB=1+;⑤S正方形ABCD=4+.其中正确结论的序号是( )
A.①③④ B.①②⑤ C.③④⑤ D.①③⑤
4.如图,过正方形的顶点作直线,点、到直线的距离分别为和,则的长为( )
A. B. C. D.
5.如图,在边长为4的正方形ABCD中,点E、F分别是边BC、CD上的动点,且BE=CF,连接BF、DE,则BF+DE的最小值为()
A. B. C. D.
6.如图,点P是边长为2cm的正方形ABCD的边上一动点,O是对角线的交点,当点P由A→D→C运动时,设DP=xcm,则△POD的面积y(cm2)随x(cm)变化的关系图象为( )
A. B.
C. D.
7.图中有三个正方形,若阴影部分面积为4个平方单位,则最大正方形的面积是( )平方单位.
A.48 B.12 C.24 D.36
8.如图,已知四边形ABCD是正方形,E是AB延长线上一点,且BE=BD,则∠BDE的度数是( )
A.22.5° B.30° C.45° D.67.5°
9.如图,点是中斜边(不与,重合)上一动点,分别作于点,作于点,连接、,若,,当点在斜边上运动时,则的最小值是( )
A.1.5 B.2
C.4.8 D.2.4
10.如图,已知矩形ABCD中,AB=3,AD=5,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t s当P,E,B三点在同一直线上时t的值为( )
A.1 B.4 C. D.2
11.如图,四边形ABCD的对角线相交于点O,且点O是BD的中点,若AB=AD=5,BD=8,∠ABD=∠CDB,则四边形ABCD的面积为( )
A.40 B.24 C.20 D.15
12.如图,在菱形中,已知,,,点在的延长线上,点在的延长线上,有下列结论:①;②;③;④若,则点到的距离为.则其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
13.如图,四边形ABCD中,∠ABC=∠BCD=∠CDA=90°,请添加一个条件_____,可得出该四边形是正方形.
14.如图,点E为正方形ABCD边CB延长线上一点,点F为AB上一点,连接AE,CF,AC,若BE=BF,∠E=70°,则∠ACF=_____.
15.如图,在矩形纸片ABCD中,AB=4,BC=4,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A'EF,连接A'C,A'D,则当△A'DC是以A'D为腰的等腰三角形时,FD的长是_____.
16.如图,直线l过正方形ABCD的顶点A,点B、D到直线l的距离分别为1、3,则正方形的边长为_______.
17.如图,在菱形中,,,点,同时由,两点出发,分别沿,方向向点匀速运动,点的运动速度为,点的运动速度为,点到达点后,点与点同时停止运动.若运动时间为秒时,为等边三角形,则的值为__________.
18.如图,在菱形c中,分别是边,对角线与边上的动点,连接,若,则的最小值是___.
19.如图,四边形ACDF是正方形,和都是直角,且点三点共线,,则阴影部分的面积是__________.
20.如图,四边形ABCD中,∠A=90°,AB=3,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为 .
三、解答题
21.已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形.
22.如图,△ABC 中,点 O 是边 AC 上一个动点,过 O 作直线 MN∥BC,设 MN 交∠ACB 的平分线于点 E,交∠ACB 的外角平分线于点 F.
(1)求证:OE=OF;
(2)当点 O 在边 AC 上运动到什么位置时,四边形 AECF 是矩形?并说明理由.
(3)若 AC 边上存在点 O,使四边形 AECF 是正方形,猜想△ABC 的形状并证明你的结论.
23.如图1,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形ABCD的外角∠DCG的平分线CF于点F.
(1)如图2,取AB的中点H,连接HE,求证:AE=EF.
(2)如图3,若点E是BC的延长线上(除C点外)的任意一点,其他条件不变结论“AE=EF”仍然成立吗?如果正确,写出证明过程:如果不正确,请说明理由.
24.已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.
(1)求证:△BGF≌△FHC;
(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.
25.如图,矩形ABCD 和正方形ECGF,其中E、H分别为AD、BC中点,连结AF、HG、AH.
(1)求证:;
(2)求证:;
26.如图,E、F、 G、H分别为四边形ABCD四边之中点.
(1)求证:四边形EFGH为平行四边形;
(2)当AC、BD满足______时,四边形EFGH为矩形.
27.如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,得到A,B的对应点C,D,连接AC,BD,CD.
(1)直接写出点C,D的坐标,求出四边形ABDC的面积;
(2)在x轴上是否存在一点F,使得三角形DFC的面积是三角形DFB面积的2倍,若存在,请求出点F的坐标;若不存在,请说明理由.
28.如图,在菱形ABCD中,点E是BC边的中点,动点M在CD边上运动,以EM为折痕将△CEM折叠得到△PEM,连接PA,若AB=4,∠BAD=60°, 求PA的最小值是.
29.如图,在正方形ABCD中,E是边AB上的一动点(不与点A、B重合),连接DE,点A关于直线DE的对称点为F,连接EF并延长交BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H,连接BH.
(1)求证:GF=GC;
(2)用等式表示线段BH与AE的数量关系,并证明.
答案
一、单选题
C.A.D.A. D.B.D.A.C.A.B.B.
二、填空题
13.AB=BC.
14.25°.
15.4-2或3.
16..
17..
18..
19.8.
20.3.
三、解答题
21.(1)在△ADE与△CDE中,
,
∴△ADE≌△CDE,
∴∠ADE=∠CDE,
∵AD∥BC,
∴∠ADE=∠CBD,
∴∠CDE=∠CBD,
∴BC=CD,
∵AD=CD,
∴BC=AD,
∴四边形ABCD为平行四边形,
∵AD=CD,
∴四边形ABCD是菱形;
(2)∵BE=BC,
∴∠BCE=∠BEC,
∵∠CBE:∠BCE=2:3,
∴∠CBE=180× =45°,
∵四边形ABCD是菱形,
∴∠ABE=45°,
∴∠ABC=90°,
∴四边形ABCD是正方形.
22.证明:(1)∵MN 交∠ACB 的平分线于点 E,交∠ACB 的外角平分线于点 F,
∴∠2=∠5,∠4=∠6,
∵MN∥BC,
∴∠1=∠5,∠3=∠6,
∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,
∴OE=OF;
(2)当点 O 在边 AC 上运动到 AC 中点时,四边形 AECF 是矩形.
证明:当 O 为 AC 的中点时,AO=CO,
∵EO=FO,
∴四边形 AECF 是平行四边形,
∵CE是∠ACB 的平分线,CF是∠ACD的平分线,
∴∠ECF= (∠ACB +∠ACD)=90°,
∴平行四边形 AECF 是矩形.
(3)△ABC 是直角三角形,
理由:∵四边形 AECF 是正方形,
∴AC⊥EN,故∠AOM=90°,
∵MN∥BC,
∴∠BCA=∠AOM,
∴∠BCA=90°,
∴△ABC 是直角三角形.
23.(1)证明:取AB的中点H,连接EH;如图1所示
∵四边形ABCD是正方形,AE⊥EF;
∴∠1+∠AEB=90°,∠2+∠AEB=90°
∴∠1=∠2,
∵BH=BE,∠BHE=45°,且∠FCG=45°,
∴∠AHE=∠ECF=135°,AH=CE,
在△AHE和△ECF中,
,
∴△AHE≌△ECF(ASA),
∴AE=EF;
(2)解:AE=EF成立,
理由如下:如图2,延长BA到M,使AM=CE,
∵∠AEF=90°,
∴∠FEG+∠AEB=90°.
∵∠BAE+∠AEB=90°,
∴∠BAE=∠FEG,
∴∠MAE=∠CEF.
∵AB=BC,
∴AB+AM=BC+CE,
即BM=BE.
∴∠M=45°,
∴∠M=∠FCE.
在△AME与△ECF中,
,
∴△AME≌△ECF(ASA),
∴AE=EF.
24.(1)连接EF,∵点F,G,H分别是BC,BE,CE的中点,
∴FH∥BE,FH=BE,FH=BG,
∴∠CFH=∠CBG,
∵BF=CF,
∴△BGF≌△FHC,
(2)当四边形EGFH是正方形时,连接GH,可得:EF⊥GH且EF=GH,
∵在△BEC中,点G,H分别是BE,CE的中点,
∴ 且GH∥BC,
∴EF⊥BC,
∵AD∥BC,AB⊥BC,
∴AB=EF=GH=a,
∴矩形ABCD的面积=
25.(1)证明:∵四边形ABCD是矩形,且E、H分别为AD、BC的中点,
∴,,
∴四边形AHCE为平行四边形,
∴,,
又∵四边形ECGF为正方形,
∴,,
∴,,
∴四边形AHGF是平行四边形,
∴;
(2)证明:∵四边形AHGF是平行四边形,
∴,
∵四边形ABCD是矩形,
∴,
∴,
又∵,
∴;
26.(1)证明:连接BD
∵E、F、 G、H分别为四边形ABCD四边的中点
∴EH是△ABD的中位线,FG是△CBD的中位线
∴EH∥BD,EH=,FG∥BD,FG=
∴EH∥FG,EH= FG
∴四边形EFGH为平行四边形;
(2)当AC⊥BD时,四边形EFGH为矩形,理由如下
连接AC,
∵E、F为BA和BC的中点
∴EF为△BAC的中位线
∴EF∥AC
∵AC⊥BD
∴EF⊥BD
∵EH∥BD
∴EF⊥EH
∴∠FEH=90°
∵四边形EFGH为平行四边形
∴四边形EFGH为矩形
故答案为:AC⊥BD.
27.(1)依题意可得C(0,2),D(4,2).S四边形ABDC=AB·OC=4×2=8.
(2)存在,
当BF=CD时,三角形DFC的面积是三角形DFB面积的2倍.
∵C(0,2),D(4,2),
∴CD=4,BF=CD=2.
∵B(3,0),
∴F(1,0)或(5,0).
28.解:根据折叠的性质得,EP=CE=BC=2,
故点P在以E为圆心,EP为半径的半圆上,
∵AP+EP≥AE,
∴当A,P,E在同一直线上时,AP最短,
如图,过点E作EF⊥AB于点F,
∵在边长为4的菱形ABCD中,∠BAD=60°,E为BC的中点,
∴BE=BC=2,∠EBF=60°,
∴∠BEF=30°,
∴BF=BE=1,
∴,AF=5,
∴
∴PA的最小值=AE﹣PE=.
故答案为:.
29.(1)证明:连接.
∵,关于对称.
∴..
在和中.
∴
∴.
∵四边形是正方形
∴.
∴
∴
∴
∵.
∴
在和.
∴≌
∴.
(2).
证明:在上取点使得,连接.
∵四这形是正方形.
∴..
∵≌
∴
同理:
∴
∵
∴
∴
∴
∴.
∵
∴
∵
∴
∴
∵.
∴
在和中
∴≌
∴
在中,,.
∴
∴.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
