九年级数学上册试题 《特殊的平行四边形》--正方形的动点问题-北师大版(含答案)
文档属性
| 名称 | 九年级数学上册试题 《特殊的平行四边形》--正方形的动点问题-北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-10 18:09:06 | ||
图片预览

文档简介
《特殊的平行四边形》--正方形的动点问题
一、单选题
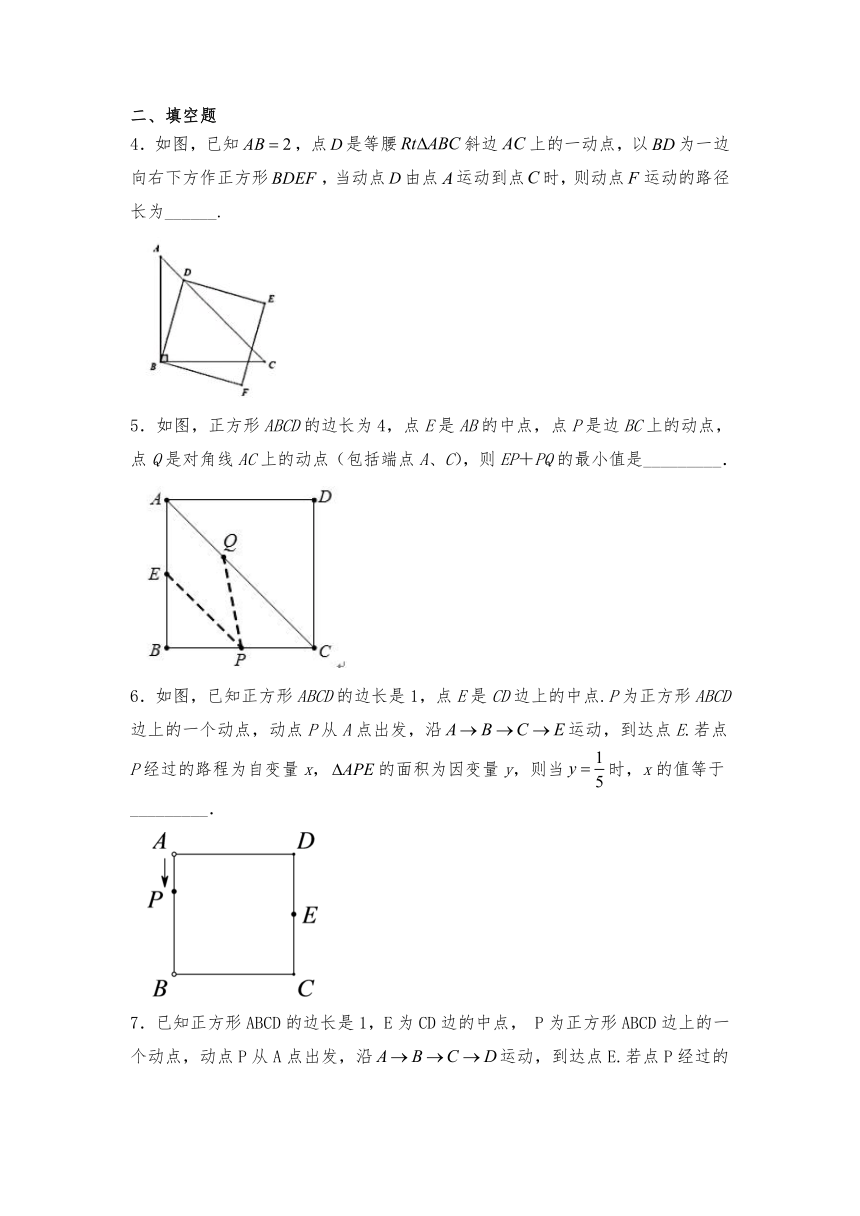
1.如图,在正方形中,是边上的动点,于点于点,则的值为( )
A. B. C. D.
2.如图,在边长为8的正方形中,、分别是边、上的动点,且,为中点,是边上的一个动点,则的最小值是( )
A.10 B. C. D.
3.如图,动点在边长为2的正方形内,且,是边上的一个动点,是边的中点,则线段的最小值为( )
A. B. C. D.
二、填空题
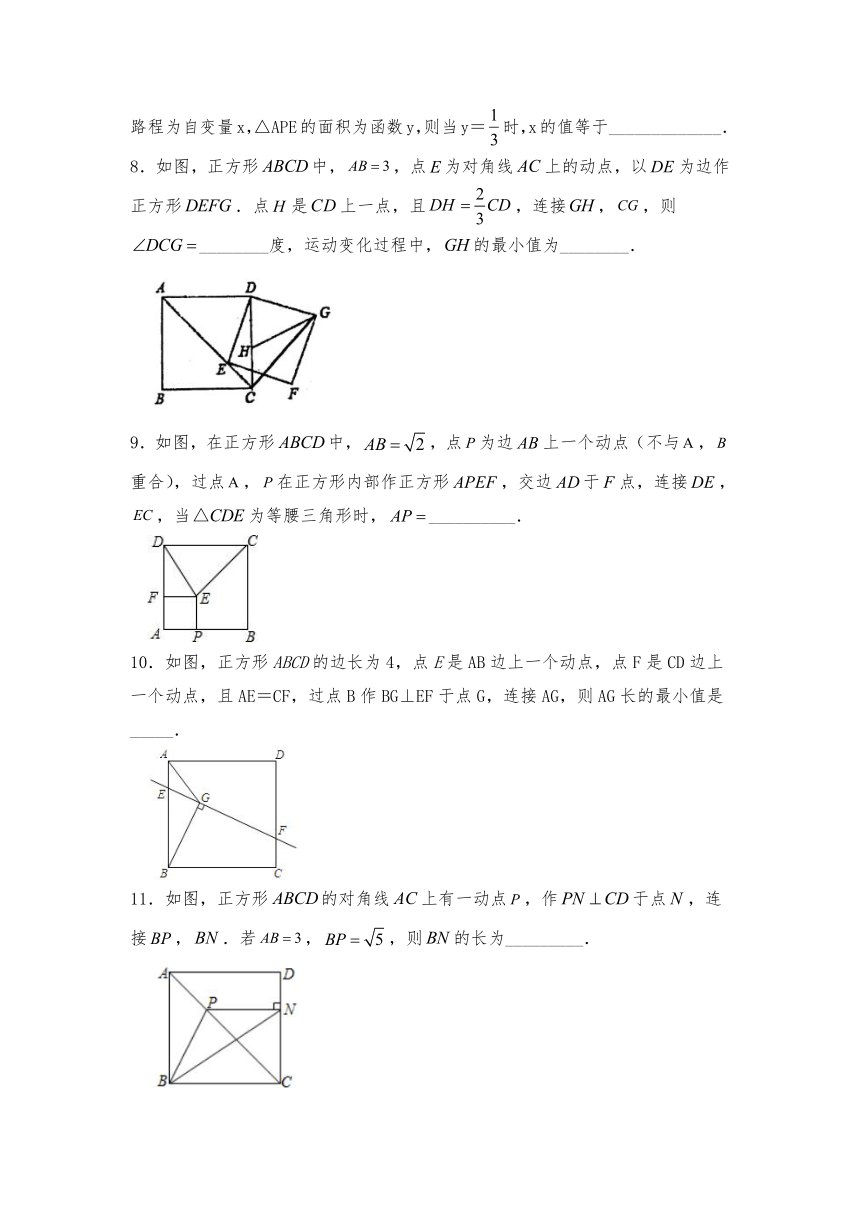
4.如图,已知,点是等腰斜边上的一动点,以为一边向右下方作正方形,当动点由点运动到点时,则动点运动的路径长为______.
5.如图,正方形ABCD的边长为4,点E是AB的中点,点P是边BC上的动点,点Q是对角线AC上的动点(包括端点A、C),则EP+PQ的最小值是_________.
6.如图,已知正方形ABCD的边长是1,点E是CD边上的中点.P为正方形ABCD边上的一个动点,动点P从A点出发,沿运动,到达点E.若点P经过的路程为自变量x,的面积为因变量y,则当时,x的值等于_________.
7.已知正方形ABCD的边长是1,E为CD边的中点, P为正方形ABCD边上的一个动点,动点P从A点出发,沿运动,到达点E.若点P经过的路程为自变量x,△APE的面积为函数y,则当y=时,x的值等于_____________.
8.如图,正方形中,,点为对角线上的动点,以为边作正方形.点是上一点,且,连接,,则________度,运动变化过程中,的最小值为________.
9.如图,在正方形中,,点为边上一个动点(不与,重合),过点,在正方形内部作正方形,交边于点,连接,,当为等腰三角形时,__________.
10.如图,正方形ABCD的边长为4,点E是AB边上一个动点,点F是CD边上一个动点,且AE=CF,过点B作BG⊥EF于点G,连接AG,则AG长的最小值是_____.
11.如图,正方形的对角线上有一动点,作于点,连接,.若,,则的长为_________.
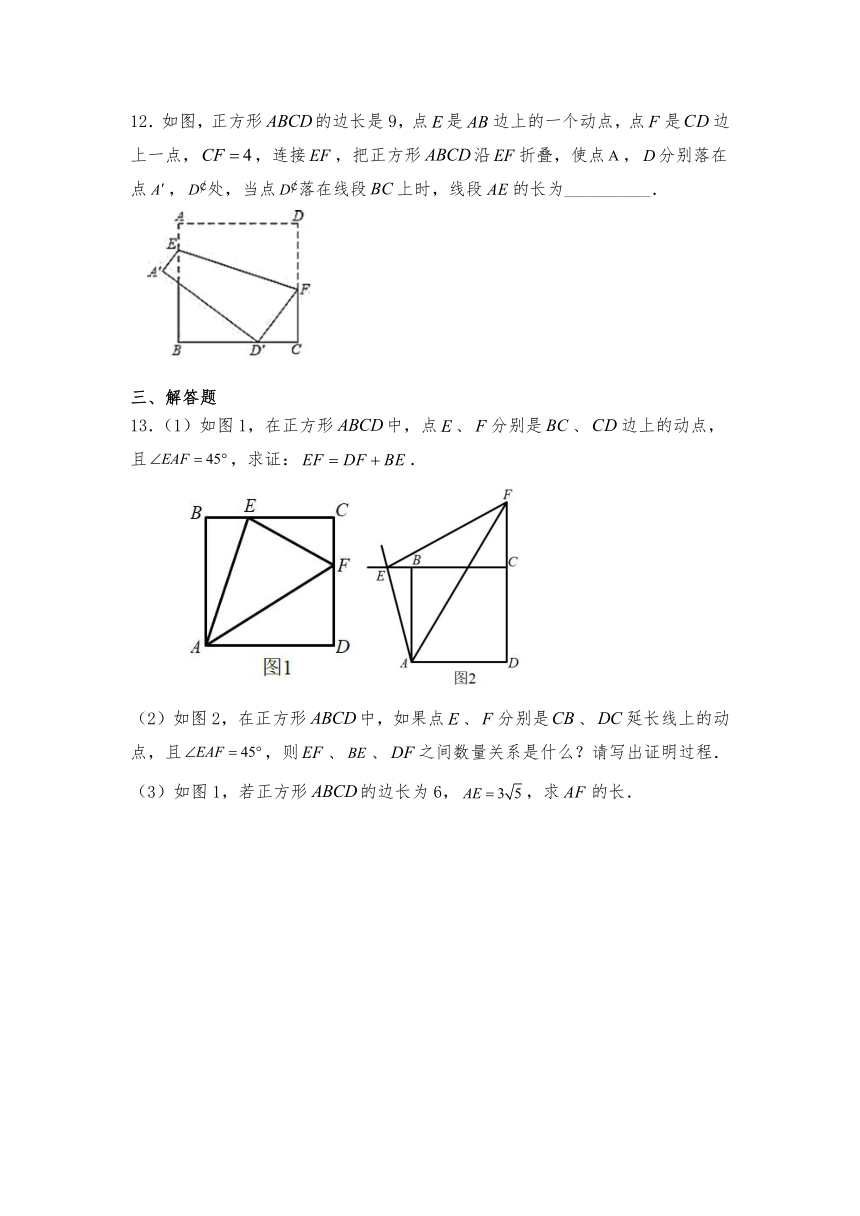
12.如图,正方形的边长是9,点是边上的一个动点,点是边上一点,,连接,把正方形沿折叠,使点,分别落在点,处,当点落在线段上时,线段的长为__________.
三、解答题
13.(1)如图1,在正方形中,点、分别是、边上的动点,且,求证:.
(2)如图2,在正方形中,如果点、分别是、延长线上的动点,且,则、、之间数量关系是什么?请写出证明过程.
(3)如图1,若正方形的边长为6,,求的长.
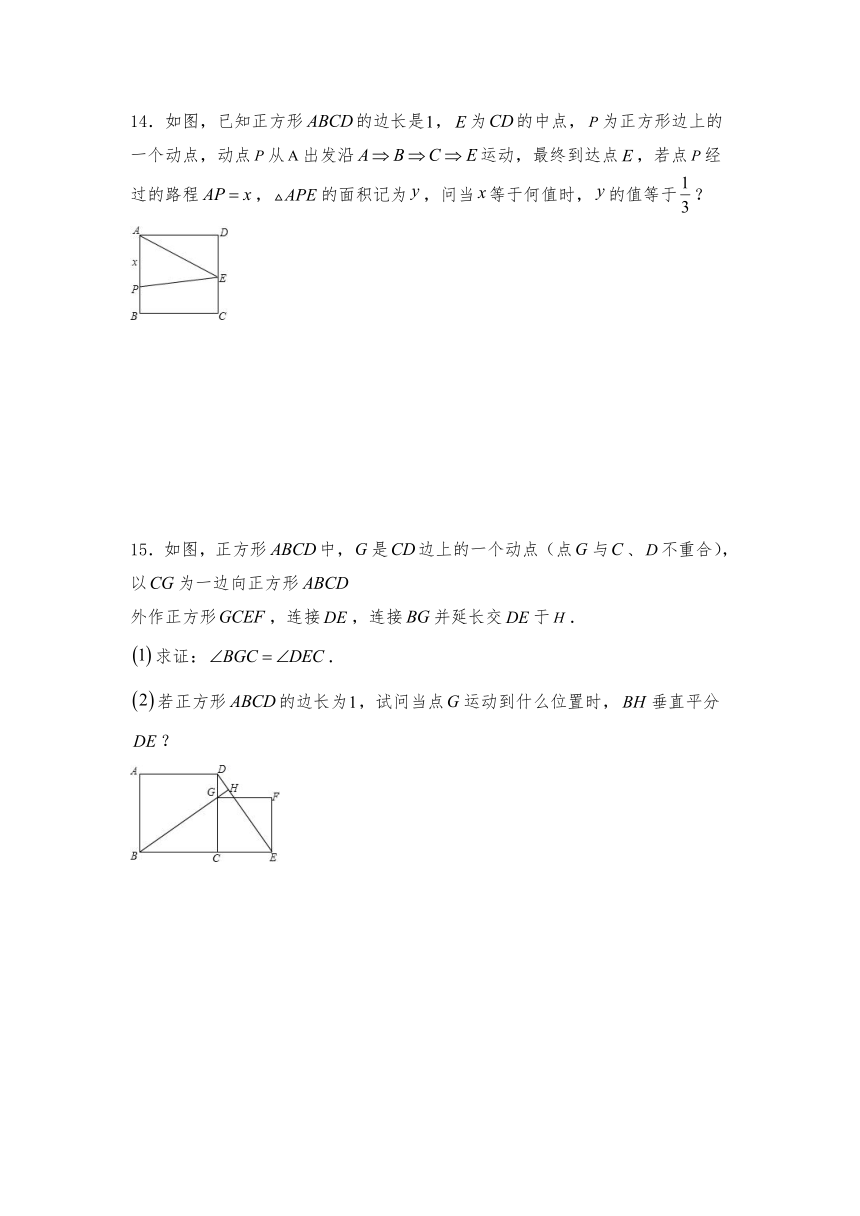
14.如图,已知正方形的边长是,为的中点,为正方形边上的一个动点,动点从出发沿运动,最终到达点,若点经过的路程,的面积记为,问当等于何值时,的值等于?
15.如图,正方形中,是边上的一个动点(点与、不重合),以为一边向正方形
外作正方形,连接,连接并延长交于.
求证:.
若正方形的边长为,试问当点运动到什么位置时,垂直平分?
16.如图,已知中,,,点为边上一动点,四边形是正方形,连接,正方形对角线交于点.
(1)求证:;
(2)若,求的值;
(3)若,求的值.
17.已知:正方形的对角线交于点,是线段上的一动点,过点作交,交于.
(1)若动点在线段上(不含端点),如图(1),求证:;
(2)若动点在线段的延长线上,如图(2),试判断的形状,并说明理由.
18.(1)如图1,在正方形ABCD中,点E、F分别是BC、CD边上的动点,且∠EAF=45°,求证:EF=DF+BE.
(2)如图2,在正方形ABCD中,如果点E、F分别是CB、DC延长线上的动点,且∠EAF=45°,则EF、BE、DF之间数量关系是什么?请写出证明过程.
(3)如图1,若正方形ABCD的边长为6,AE=3,求AF的长.
19.如图所示,,分别是正方形的边,上的两个动点,且,交于点,,连.求证:.
20.已知,如图所示,正方形的边长为1,为边上的一个动点(点与、不重合),以为一边向正方形外作正方形,连接交的延长线于点.
(1)求证:①≌△. ②.
(2)当平分时,求的长.
21.在中,,分别以,为边向外作正方形和正方形.
(1)当时,正方形的周长=_______(用含的代数式表示);
(2)连接.试说明:三角形的面积等于正方形面积的一半.
(3)已知,且点是线段上的动点,点是线段上的动点,当点和点在移动过程中,的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
22.如图,是正方形的边上的两个动点,满足相交于点与相交于点,连接.
(1)求证:;
(2)若正方形的边长为4,求的最小值.
23.已知正方形ABCD的对角线AC与BD交于点O,点E、F分别是OB、OC上的动点,
(1)如果动点E、F满足BE=CF(如图):
①写出所有以点E或F为顶点的全等三角形(不得添加辅助线);
②证明:AE⊥BF;
(2)如果动点E、F满足BE=OF(如图),问当AE⊥BF时,点E在什么位置,并证明你的结论.
24.在正方形中,点是边的中点,点是对角线上的动点,连接,过点作交正方形的边于点;
(1)当点在边上时,①判断与的数量关系;
②当时,判断点的位置;
(2)若正方形的边长为2,请直接写出点在边上时,的取值范围.
答案
一、单选题
C.B.A.
二、填空题
4.
5.
6.或或
7.或
8.45°
9.或
10.
11.或
12.2
三、解答题
13.
(1)证明:把绕点顺时针旋转90°至,
如图1,∴,,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴;
(2)结论:;
证明:如图2,将绕点顺时针旋转90°至,
∴,,,,
∴,
∵,
∴,
∴;
(3)解:由(1)可知,
∵正方形的边长为6,
∴,
∴.
∴,
∴,
设,则,,
在中,∵,
∴,
解得:.
∴,
∴.
14.解:由题意可知:当动点从运动到时,,
当动点从运动到时,,由于,
因此满足题意的点的位置只有两种情况
①当时,即点在边上运动时,如图,此时,
,当时,解得:
②当时,即点在边上运动,如图,此时折线,,
当时,解得:
综上所述,当或时,的面积为
15.(1)证明:∵四边形、都是正方形,
∴,,
∴
∴连接
如果垂直平分,则有
∵,
∴
∴
∴
即当时,垂直平分.
16.(1)证明:四边形是正方形
,
在和中
故答案为
(2),,
在中
由(1)知,
,
连接
在中
四边形是正方形
故答案为
(3)如图所示,连接FG
四边形是正方形
,
由(1)知,
,,
在和中
设,则
由(2)知
在中
,
的值为或.
故答案为或
17.
(1)证明:∵四边形为正方形,
∴,,
∴∠OBE+∠OEG=90°,
∵于点,
∴,
∴∠OAF+∠OEG=90°,
∴,
在和中,
∴,
∴;
(2)解:是等腰直角三角形,理由如下:
∵四边形为正方形,
∴,,
∴∠OBE+∠OEG=90°,
∵于点,
∴,
∴∠OAF+∠OEG=90°,
∴,
在和中,
∴
∴;
又∵,
∴是等腰直角三角形.
18.
(1)把△ABE绕点A顺时针旋转90°至△ADG,如图1,
∴∠BAE=∠DAG,AE=AG,
∵∠EAF=45°,
∴∠BAE+∠FAD=45°,
∴∠DAG+∠FAD=45°,
∴∠EAF=∠FAG,
∵AF=AF,
∴△EAF≌△GAF(SAS),
∴EF=FG=DF+DG,
∴EF=DF+BE;
(2)结论:EF=DF﹣BE;
证明:如图2,将△ABE绕点A顺时针旋转90°至△ADM,
∴∠EAB=∠MAD,AE=AM,∠EAM=90°,BE=DM,
∴∠FAM=45°=∠EAF,
∵AF=AF,
∴△EAF≌△MAF(SAS),
∴EF=FM=DF﹣DM=DF﹣BE;
(3)如图,
由(1)可得AE=AG=,EF=FG,BE=DG,
∵DG=,
∴BE=DG=3,
∴EC=BC﹣BE=3,
∵EF2=EC2+CF2,
∴(DF+3)2=9+(6﹣DF)2,
∴DF=2,
∴AF===2.
19.证明: ∵四边形ABCD是正方形,
∴AB=DA,∠BAD=∠ADF=90°,
又∵AE=DF,
∴△ABE≌△DAF,
∴∠ABE=∠DAF.
∴∠DAF+∠BAH=∠ABE+∠BAH=90°,
∴∠AHB=90°,
∴AF⊥BE.
20.
(1)①∵四边形与四边形均为正方形,
∴BC=CD,CE=CG,∠BCD=∠ECG=900,
∴≌△
②∵≌△,
∴∠BGC=∠DEC,
∵∠BGC+∠CBG=900,
∴∠DEC+∠CGB=900
∴∠BHE=900
即
(2) 连接BD,
∵四边形ABCD是正方形,边长为1,
∴AB=AD=1,∠A=900,
∴
∵BH平分DE,BH⊥DE,
∴DH=EH,∠BHD=∠BHE,
又∵BH=BH
∴△BHD≌△BHE,
∴BE=BD=,
∴CG=CE=BE-BC=.
21.
(1)∵四边形BCFH是正方形,
∴BC=BH=FH=CF,
∴当BC=m时,正方形BCFH的周长为4m,
故答案为:4m;
(2)如图1,连接AH,
在△BHA和△BCE中,
∴△BHA≌△BCE(SAS),
∵AF∥BH,
∴BH边上的高=正方形BCFH的边
∴△BHA的面积等于正方形BCFH的面积.
∴△AEC的面积等于正方形BCFH的面积;
(3)△APQ的周长存在最小值.
如图2,作点A关于DE的对称点A
∴AP=A′P
∵点A关于BC的对称点F,
∴AQ=QF,
∴△APQ的周长的最小值为A′F,
过A′作A′M⊥FA交FA的延长线于M,
∵,
∴∠BAC=45°,AB=2
∴∠A′AM=45°, AA′=4,
∴△AA′M为等腰直角三角形,,
∴MA=MA′=4,
∴MF=8,
∴A′F==4,
∴△APQ的周长的最小值为4.
22.
(1)证明:是正方形,
又
(2)取中点,连接
由(1),得
在中,由勾股定理,得
的最小值.
23.
(1)①△ABE≌△BCF, △AOE≌△BOF, △ABF≌△DEA
②证明:如图,延长AE 交BF 于点M,
∵ABCD 是正方形,∴AB=BC, ∠BCF=∠ABE.
∵BE=CF,∴△ABE≌△BCF(SAS).∴∠CBF=∠BAE
∵∠ABE+∠EBM+∠CBF=90°,
∴∠ABE+∠EBM+∠BAE =90°.
∴∠AMB=90°.∴AE⊥BF.
(2)点E 是OB 的中点.证明如下:
∵ABCD 是正方形,∴AB=BC, ∠BCF=∠ABE.
∵AE⊥BF,∴∠AMB=90°.∴∠ABE+∠EBM+∠BAE =90°.
∴∠ABE+∠EBM+∠CBF=90°.∴∠CBF=∠BAE.∴△ABE≌△BCF(ASA).
∴BE=CF.
∵BE=OF,∴CF=OF.
又∵OB=OC,∴BE=OE.∴点E是OB 的中点.
24.
解:(1).理由是:
过点作于点,于点
在正方形中,
矩形为正方形
又
②点位于正方形两条对角线的交点处(或中点处)
如图,是的中位线,
又,
此时,是中点,
且,
,
(2)当点F与 B重合时,M在AC,BD交点处时,此时AM最小, AM=AC= ; 当点F与点C重合时,M在AC,BD交点到点C的中点处,此时AM最大, AM= .
故答案为
一、单选题
1.如图,在正方形中,是边上的动点,于点于点,则的值为( )
A. B. C. D.
2.如图,在边长为8的正方形中,、分别是边、上的动点,且,为中点,是边上的一个动点,则的最小值是( )
A.10 B. C. D.
3.如图,动点在边长为2的正方形内,且,是边上的一个动点,是边的中点,则线段的最小值为( )
A. B. C. D.
二、填空题
4.如图,已知,点是等腰斜边上的一动点,以为一边向右下方作正方形,当动点由点运动到点时,则动点运动的路径长为______.
5.如图,正方形ABCD的边长为4,点E是AB的中点,点P是边BC上的动点,点Q是对角线AC上的动点(包括端点A、C),则EP+PQ的最小值是_________.
6.如图,已知正方形ABCD的边长是1,点E是CD边上的中点.P为正方形ABCD边上的一个动点,动点P从A点出发,沿运动,到达点E.若点P经过的路程为自变量x,的面积为因变量y,则当时,x的值等于_________.
7.已知正方形ABCD的边长是1,E为CD边的中点, P为正方形ABCD边上的一个动点,动点P从A点出发,沿运动,到达点E.若点P经过的路程为自变量x,△APE的面积为函数y,则当y=时,x的值等于_____________.
8.如图,正方形中,,点为对角线上的动点,以为边作正方形.点是上一点,且,连接,,则________度,运动变化过程中,的最小值为________.
9.如图,在正方形中,,点为边上一个动点(不与,重合),过点,在正方形内部作正方形,交边于点,连接,,当为等腰三角形时,__________.
10.如图,正方形ABCD的边长为4,点E是AB边上一个动点,点F是CD边上一个动点,且AE=CF,过点B作BG⊥EF于点G,连接AG,则AG长的最小值是_____.
11.如图,正方形的对角线上有一动点,作于点,连接,.若,,则的长为_________.
12.如图,正方形的边长是9,点是边上的一个动点,点是边上一点,,连接,把正方形沿折叠,使点,分别落在点,处,当点落在线段上时,线段的长为__________.
三、解答题
13.(1)如图1,在正方形中,点、分别是、边上的动点,且,求证:.
(2)如图2,在正方形中,如果点、分别是、延长线上的动点,且,则、、之间数量关系是什么?请写出证明过程.
(3)如图1,若正方形的边长为6,,求的长.
14.如图,已知正方形的边长是,为的中点,为正方形边上的一个动点,动点从出发沿运动,最终到达点,若点经过的路程,的面积记为,问当等于何值时,的值等于?
15.如图,正方形中,是边上的一个动点(点与、不重合),以为一边向正方形
外作正方形,连接,连接并延长交于.
求证:.
若正方形的边长为,试问当点运动到什么位置时,垂直平分?
16.如图,已知中,,,点为边上一动点,四边形是正方形,连接,正方形对角线交于点.
(1)求证:;
(2)若,求的值;
(3)若,求的值.
17.已知:正方形的对角线交于点,是线段上的一动点,过点作交,交于.
(1)若动点在线段上(不含端点),如图(1),求证:;
(2)若动点在线段的延长线上,如图(2),试判断的形状,并说明理由.
18.(1)如图1,在正方形ABCD中,点E、F分别是BC、CD边上的动点,且∠EAF=45°,求证:EF=DF+BE.
(2)如图2,在正方形ABCD中,如果点E、F分别是CB、DC延长线上的动点,且∠EAF=45°,则EF、BE、DF之间数量关系是什么?请写出证明过程.
(3)如图1,若正方形ABCD的边长为6,AE=3,求AF的长.
19.如图所示,,分别是正方形的边,上的两个动点,且,交于点,,连.求证:.
20.已知,如图所示,正方形的边长为1,为边上的一个动点(点与、不重合),以为一边向正方形外作正方形,连接交的延长线于点.
(1)求证:①≌△. ②.
(2)当平分时,求的长.
21.在中,,分别以,为边向外作正方形和正方形.
(1)当时,正方形的周长=_______(用含的代数式表示);
(2)连接.试说明:三角形的面积等于正方形面积的一半.
(3)已知,且点是线段上的动点,点是线段上的动点,当点和点在移动过程中,的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
22.如图,是正方形的边上的两个动点,满足相交于点与相交于点,连接.
(1)求证:;
(2)若正方形的边长为4,求的最小值.
23.已知正方形ABCD的对角线AC与BD交于点O,点E、F分别是OB、OC上的动点,
(1)如果动点E、F满足BE=CF(如图):
①写出所有以点E或F为顶点的全等三角形(不得添加辅助线);
②证明:AE⊥BF;
(2)如果动点E、F满足BE=OF(如图),问当AE⊥BF时,点E在什么位置,并证明你的结论.
24.在正方形中,点是边的中点,点是对角线上的动点,连接,过点作交正方形的边于点;
(1)当点在边上时,①判断与的数量关系;
②当时,判断点的位置;
(2)若正方形的边长为2,请直接写出点在边上时,的取值范围.
答案
一、单选题
C.B.A.
二、填空题
4.
5.
6.或或
7.或
8.45°
9.或
10.
11.或
12.2
三、解答题
13.
(1)证明:把绕点顺时针旋转90°至,
如图1,∴,,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴;
(2)结论:;
证明:如图2,将绕点顺时针旋转90°至,
∴,,,,
∴,
∵,
∴,
∴;
(3)解:由(1)可知,
∵正方形的边长为6,
∴,
∴.
∴,
∴,
设,则,,
在中,∵,
∴,
解得:.
∴,
∴.
14.解:由题意可知:当动点从运动到时,,
当动点从运动到时,,由于,
因此满足题意的点的位置只有两种情况
①当时,即点在边上运动时,如图,此时,
,当时,解得:
②当时,即点在边上运动,如图,此时折线,,
当时,解得:
综上所述,当或时,的面积为
15.(1)证明:∵四边形、都是正方形,
∴,,
∴
∴连接
如果垂直平分,则有
∵,
∴
∴
∴
即当时,垂直平分.
16.(1)证明:四边形是正方形
,
在和中
故答案为
(2),,
在中
由(1)知,
,
连接
在中
四边形是正方形
故答案为
(3)如图所示,连接FG
四边形是正方形
,
由(1)知,
,,
在和中
设,则
由(2)知
在中
,
的值为或.
故答案为或
17.
(1)证明:∵四边形为正方形,
∴,,
∴∠OBE+∠OEG=90°,
∵于点,
∴,
∴∠OAF+∠OEG=90°,
∴,
在和中,
∴,
∴;
(2)解:是等腰直角三角形,理由如下:
∵四边形为正方形,
∴,,
∴∠OBE+∠OEG=90°,
∵于点,
∴,
∴∠OAF+∠OEG=90°,
∴,
在和中,
∴
∴;
又∵,
∴是等腰直角三角形.
18.
(1)把△ABE绕点A顺时针旋转90°至△ADG,如图1,
∴∠BAE=∠DAG,AE=AG,
∵∠EAF=45°,
∴∠BAE+∠FAD=45°,
∴∠DAG+∠FAD=45°,
∴∠EAF=∠FAG,
∵AF=AF,
∴△EAF≌△GAF(SAS),
∴EF=FG=DF+DG,
∴EF=DF+BE;
(2)结论:EF=DF﹣BE;
证明:如图2,将△ABE绕点A顺时针旋转90°至△ADM,
∴∠EAB=∠MAD,AE=AM,∠EAM=90°,BE=DM,
∴∠FAM=45°=∠EAF,
∵AF=AF,
∴△EAF≌△MAF(SAS),
∴EF=FM=DF﹣DM=DF﹣BE;
(3)如图,
由(1)可得AE=AG=,EF=FG,BE=DG,
∵DG=,
∴BE=DG=3,
∴EC=BC﹣BE=3,
∵EF2=EC2+CF2,
∴(DF+3)2=9+(6﹣DF)2,
∴DF=2,
∴AF===2.
19.证明: ∵四边形ABCD是正方形,
∴AB=DA,∠BAD=∠ADF=90°,
又∵AE=DF,
∴△ABE≌△DAF,
∴∠ABE=∠DAF.
∴∠DAF+∠BAH=∠ABE+∠BAH=90°,
∴∠AHB=90°,
∴AF⊥BE.
20.
(1)①∵四边形与四边形均为正方形,
∴BC=CD,CE=CG,∠BCD=∠ECG=900,
∴≌△
②∵≌△,
∴∠BGC=∠DEC,
∵∠BGC+∠CBG=900,
∴∠DEC+∠CGB=900
∴∠BHE=900
即
(2) 连接BD,
∵四边形ABCD是正方形,边长为1,
∴AB=AD=1,∠A=900,
∴
∵BH平分DE,BH⊥DE,
∴DH=EH,∠BHD=∠BHE,
又∵BH=BH
∴△BHD≌△BHE,
∴BE=BD=,
∴CG=CE=BE-BC=.
21.
(1)∵四边形BCFH是正方形,
∴BC=BH=FH=CF,
∴当BC=m时,正方形BCFH的周长为4m,
故答案为:4m;
(2)如图1,连接AH,
在△BHA和△BCE中,
∴△BHA≌△BCE(SAS),
∵AF∥BH,
∴BH边上的高=正方形BCFH的边
∴△BHA的面积等于正方形BCFH的面积.
∴△AEC的面积等于正方形BCFH的面积;
(3)△APQ的周长存在最小值.
如图2,作点A关于DE的对称点A
∴AP=A′P
∵点A关于BC的对称点F,
∴AQ=QF,
∴△APQ的周长的最小值为A′F,
过A′作A′M⊥FA交FA的延长线于M,
∵,
∴∠BAC=45°,AB=2
∴∠A′AM=45°, AA′=4,
∴△AA′M为等腰直角三角形,,
∴MA=MA′=4,
∴MF=8,
∴A′F==4,
∴△APQ的周长的最小值为4.
22.
(1)证明:是正方形,
又
(2)取中点,连接
由(1),得
在中,由勾股定理,得
的最小值.
23.
(1)①△ABE≌△BCF, △AOE≌△BOF, △ABF≌△DEA
②证明:如图,延长AE 交BF 于点M,
∵ABCD 是正方形,∴AB=BC, ∠BCF=∠ABE.
∵BE=CF,∴△ABE≌△BCF(SAS).∴∠CBF=∠BAE
∵∠ABE+∠EBM+∠CBF=90°,
∴∠ABE+∠EBM+∠BAE =90°.
∴∠AMB=90°.∴AE⊥BF.
(2)点E 是OB 的中点.证明如下:
∵ABCD 是正方形,∴AB=BC, ∠BCF=∠ABE.
∵AE⊥BF,∴∠AMB=90°.∴∠ABE+∠EBM+∠BAE =90°.
∴∠ABE+∠EBM+∠CBF=90°.∴∠CBF=∠BAE.∴△ABE≌△BCF(ASA).
∴BE=CF.
∵BE=OF,∴CF=OF.
又∵OB=OC,∴BE=OE.∴点E是OB 的中点.
24.
解:(1).理由是:
过点作于点,于点
在正方形中,
矩形为正方形
又
②点位于正方形两条对角线的交点处(或中点处)
如图,是的中位线,
又,
此时,是中点,
且,
,
(2)当点F与 B重合时,M在AC,BD交点处时,此时AM最小, AM=AC= ; 当点F与点C重合时,M在AC,BD交点到点C的中点处,此时AM最大, AM= .
故答案为
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
