九年级数学上册试题 《特殊的平行四边形》--正方形的折叠问题-北师大版(含答案)
文档属性
| 名称 | 九年级数学上册试题 《特殊的平行四边形》--正方形的折叠问题-北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 578.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-10 18:10:15 | ||
图片预览



文档简介
《特殊的平行四边形》--正方形的折叠问题
一、单选题
1.如图,把正方形纸片沿对边中点所在的直线对折后展开,折痕为MN,再过点C折叠纸片,使点C落在MN上的点F处,折痕为BE.若AB的长为1,则FM的长为( )
A.1 B. C. D.
2.如图,四边形是边长为9的正方形纸片,将其沿折叠,使点落在边上的处,点的对应点为,且,则的长是( )
A.1 B.1.5 C.2 D.2.5
3.如图,在正方形中,为边上的一点,沿线段对折后,若比大,则的度数为( )
A. B. C. D.
4.如图,已知正方形,沿直线将折起,使点A落在对角线上的处,连结,则( )
A.45° B.60° C.67.5° D.75°
5.如图,在正方形纸片上,是上一点(不与点重合),将纸片沿折叠,使点落在点处,延长交于点,则( )
A. B. C. D.不是定值
6.如图,正方形中,点E为中点,连结,将沿翻折得到,连结并延长交于点G,若,则的长为( )
A. B. C. D.
7.如图,在正方形中,是边上的一点,,,将正方形边沿折叠到,延长交于点,连接,,如下4个结论:;②为中点;③;④.其中正确结论的有( )
A.1个 B.2个 C.3个 D.4个
8.如图,在正方形ABCD中,AB=6,点E,F分别在边AB,CD上,∠EFC=120°.若将四边形EBCF沿EF折叠,点B恰好落在AD边上,则AE的长度为( )
A.2 B. C. D.1
9.如图,折叠矩形纸片ABCD,先把△ABF沿AF翻折,点B落在AD边上的点E处,折痕为AF,点F在BC边上,然后将纸片展开铺平,把四边形NCDM翻折,点C恰好落在AE的中点G处,折痕为MN,则( )
A.当点N与点F重合时,∠AFM=90°
B.当GN∥AF时,∠HMG=45°
C.若AB=2,AD=3,则M恰好为DE的中点
D.△GMN的面积有可能为矩形ABCD面积的一半
10.如图.已知正方形的边长为.,将正方形的边沿折叠到,延长交于,连接.现有如下个结论;①;②;③的周长是.其中正确的个数为( )
A. B. C. D.
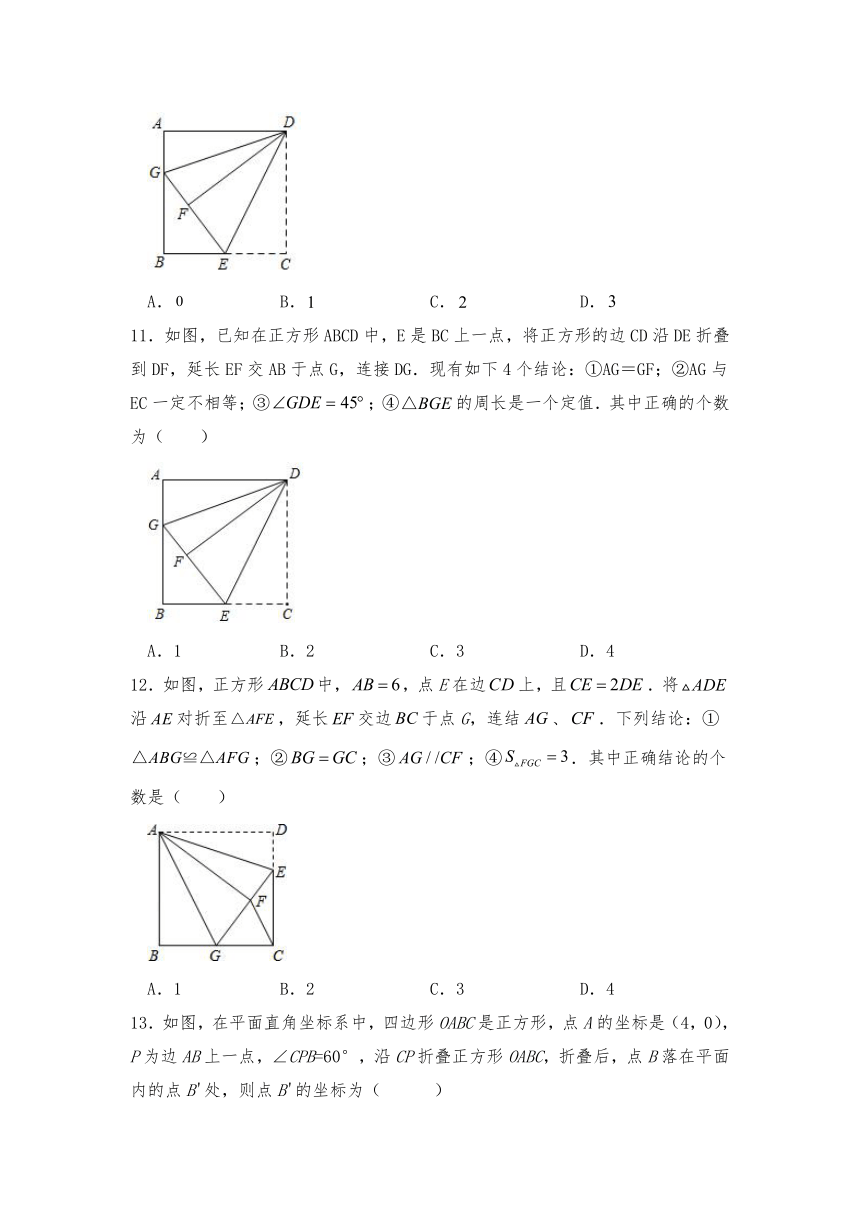
11.如图,已知在正方形ABCD中,E是BC上一点,将正方形的边CD沿DE折叠到DF,延长EF交AB于点G,连接DG.现有如下4个结论:①AG=GF;②AG与EC一定不相等;③;④的周长是一个定值.其中正确的个数为( )
A.1 B.2 C.3 D.4
12.如图,正方形中,,点E在边上,且.将沿对折至,延长交边于点G,连结、.下列结论:①;②;③;④.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
13.如图,在平面直角坐标系中,四边形OABC是正方形,点A的坐标是(4,0),P为边AB上一点,∠CPB=60°,沿CP折叠正方形OABC,折叠后,点B落在平面内的点B'处,则点B'的坐标为( )
A.(2,) B.(,) C.(2,) D.(,)
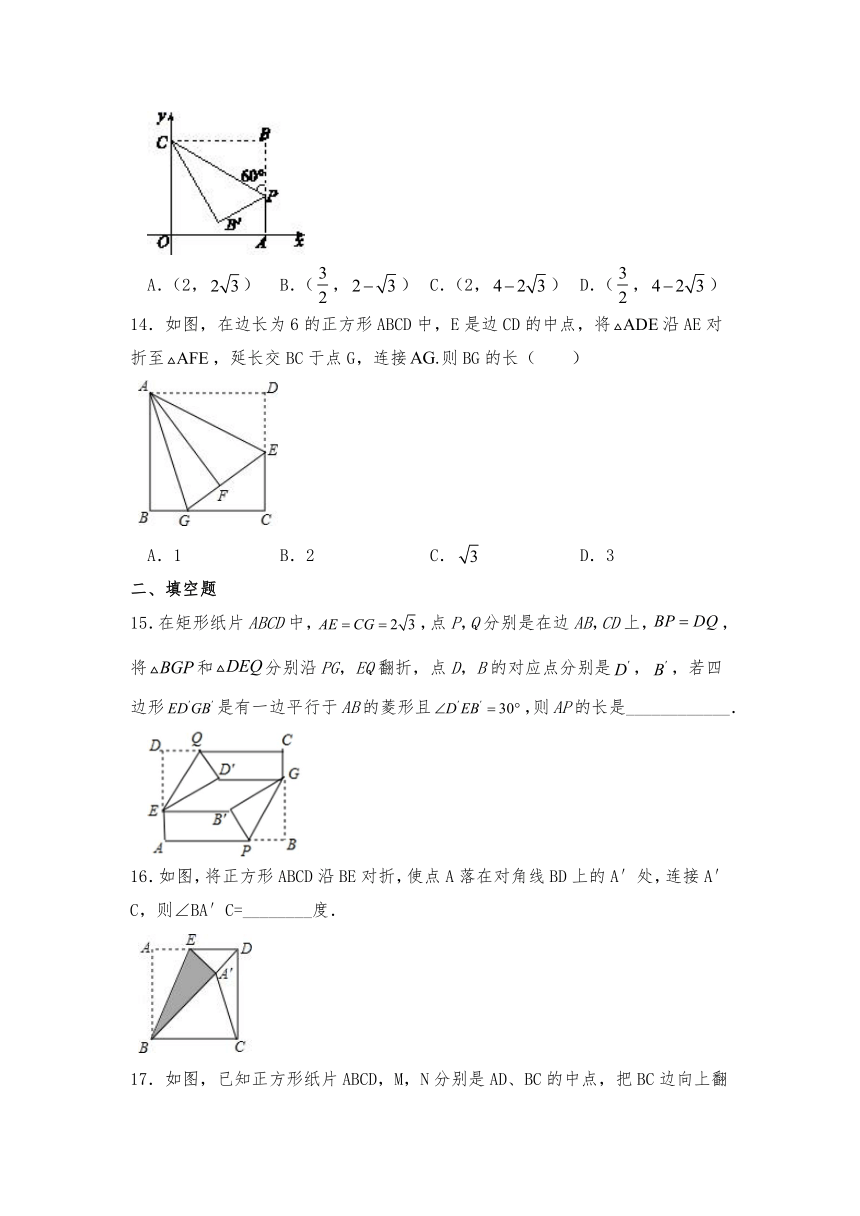
14.如图,在边长为6的正方形ABCD中,E是边CD的中点,将沿AE对折至,延长交BC于点G,连接则BG的长( )
A.1 B.2 C. D.3
二、填空题
15.在矩形纸片ABCD中,,点P,Q分别是在边AB,CD上,,将和分别沿PG,EQ翻折,点D,B的对应点分别是,,若四边形是有一边平行于AB的菱形且,则AP的长是____________.
16.如图,将正方形ABCD沿BE对折,使点A落在对角线BD上的A′处,连接A′C,则∠BA′C=________度.
17.如图,已知正方形纸片ABCD,M,N分别是AD、BC的中点,把BC边向上翻折,使点C恰好落在MN上的P点处,BQ为折痕,则∠PBQ=_____度.
18.如图在正方形中,,将沿翻折,使点对应点刚好落在对角线上,将沿翻折,使点对应点落在对角线上,求______.
19.如图,正方形ABCD中,,点E在边CD上,且将沿AE对折至,延长EF交边BC于点G,连接AG、则的面积是______.
20.如图,在正方形纸片 ABCD 中, E 是 CD 的中点,将正方形纸片折叠,点 B 落在线段AE 上的点 G 处,折痕为 AF .若 AD=4 cm,则 CF 的长为___________cm .
21.如图,四边形是一张正方形纸片,其面积为.分别在边,,,上顺次截取,连接,,,.分别以,,,为轴将纸片向内翻折,得到四边形,若四边形的面积为,则__________.
22.如图,将边长为9的正方形纸片ABCD沿MN折叠,使点A落在BC边上点处,点D的对应点为点,若,则DM=__________.
23.如图,将边长为4的正方形纸片ABCD折叠,使得点落在边CD的中点E处,折痕为FG,点F、G分别在边AD、BC上,则折痕FG的长度为_________.
24.如图,正方形ABCD中,AB=6,E是CD的中点,将△ADE沿AE翻折至△AFE,连接CF,则CF的长度是_____.
25.如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB'E,AB'与CD边交于点F,则B'F的长度为_______
26.如图,在正方形ABCD中,BE=EC,将正方形ABCD的边CD沿DE折叠到DF,连接EF、FC、FB,若△DFC的面积为16,则△BEF的面积为_____.
27.如图,正方形ABCD中,AD=+2,已知点E是边AB上的一动点(不与A、B重合)将△ADE沿DE对折,点A的对应点为P,当△APB是等腰三角形时,AE=_____.
28.如图,正方形 中,,是 的中点.将 沿 对折至 , 延长 交 于点 ,则 的长是____.
29.如图,在正方形ABCD中,E是BC边上的一点,BE=4,EC=8,将正方形边AB沿AE折叠到AF,延长EF交DC于G,连接AG,现在有如下四个结论:①∠EAG=45°;②FG=FC;③FC∥AG;④S△GFC=14.其中结论正确的序号是_____.
30.如图,正方形的边长是16,点在边上,,点是边上不与点、重合的一个动点,把沿折叠,点落在处,若恰为等腰三角形,则的长为______.
三、解答题
31.如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
(1)求证:△ABG≌△AFG;
(2)求∠EAG的度数;
(3)求BG的长.
32.如图,在矩形ABCD中,2AB>BC,点E和点F为边AD上两点,将矩形沿着BE和CF折叠,点A和点D恰好重合于矩形内部的点G处,
(1)当AB=BC时,求∠GEF的度数;
(2)若AB=,BC=2,求EF的长.
33.如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.
(1)求证:①△ABG≌△AFG; ②BG=GC;
(2)求△FGC的面积.
34.如图,正方形ABCD中,,点E在CD上,且,将沿AE对折至,延长EF交BC于点G,连接AG、CF.
求证:≌;
求BG的长;
求的面积.
答案
一、单选题
B.C.C.C.B.C.D.A.B.D.C.C.C.B.
二、填空题
15.或3
16.67.5.
17.30.
18.
19.
20.
21.4
22.
23.2.
24.
25.
26.4
27.1或
28.4
29.①③.
30.16或
三、解答题
31.
(1)证明;在正方形ABCD中,AD=AB=BC=CD,∠D=∠B=∠BCD=90°,
∵将△ADE沿AE对折至△AFE,
∴AD=AF,DE=EF,∠D=∠AFE=90°,
∴AB=AF,∠B=∠AFG=90°,
又∵AG=AG,
在Rt△ABG和Rt△AFG中,
,
∴△ABG≌△AFG(HL);
(2)∵△ABG≌△AFG,
∴∠BAG=∠FAG,
∴∠FAG=∠BAF,
由折叠的性质可得:∠EAF=∠DAE,
∴∠EAF=∠DAF,
∴∠EAG=∠EAF+∠FAG=(∠DAF+∠BAF)=∠DAB=×90°=45°;
(3)∵E是CD的中点,
∴DE=CE=CD=×6=3,
设BG=x,则CG=6﹣x,GE=EF+FG=x+3,
∵GE2=CG2+CE2
∴(x+3)2=(6﹣x)2+32,
解得:x=2,
∴BG=2.
32.
解:(1)当AB=BC时,矩形ABCD为正方形,
由折叠得,AB=BG,CD=CG;∠EGB=∠A=90°,
∵AB=BC=CD,
∴BG=BC=GC,
∴∠BGC=60°,
∴∠ABG=30°,
∴∠AEG=150°,
∴∠GEF=30°;
(2)在矩形ABCD中,AB=CD=,
由折叠得,AB=BG,CD=CG,AE=EG,DF=FG,
∴BG=GC=,
又∵BC=2,
得△BGC为等腰直角三角形,且∠GBC=45°,
与(1)同理可得∠FEG=45°,∠EFG=45°,△EGF为等腰直角三角形 ,
设EG=x,则AE=FD=x,EF=,得,
(2+)x=2 ,得x=,
∴EF= .
33.
(1)证明:
①在正方形ABCD中,AD=AB,∠D=∠B=∠C=90
又∵△ADE沿AE对折至△AFE,延长EF交边BC于点G
∴∠AFG=∠AFE=∠D=90 ,AF=AD,
即有∠B=∠AFG=90 ,AB=AF,AG=AG,
∴△ABG≌△AFG
②∵AB=6,点E在边CD上,且CD=3DE,∴DE=FE=2,CE=4
不妨设BG=FG=x,(x>0),则CG=6-x,EG=2+x,
在Rt△CEG中,(2+x)2=42+(6-x)2
解得x=3,于是BG=GC=3
(2)∵,∴
∴S△FGC=S△EGC=
34.是由折叠得到,
,,
又四边形ABCD是正方形,
,,
,,
在和中,
≌,
正方形ABCD中,,,
,
设,则.
在直角中,根据勾股定理,得,
解得.
;
由知,,,
由知,≌,
,
,
由知,,,
,
.
一、单选题
1.如图,把正方形纸片沿对边中点所在的直线对折后展开,折痕为MN,再过点C折叠纸片,使点C落在MN上的点F处,折痕为BE.若AB的长为1,则FM的长为( )
A.1 B. C. D.
2.如图,四边形是边长为9的正方形纸片,将其沿折叠,使点落在边上的处,点的对应点为,且,则的长是( )
A.1 B.1.5 C.2 D.2.5
3.如图,在正方形中,为边上的一点,沿线段对折后,若比大,则的度数为( )
A. B. C. D.
4.如图,已知正方形,沿直线将折起,使点A落在对角线上的处,连结,则( )
A.45° B.60° C.67.5° D.75°
5.如图,在正方形纸片上,是上一点(不与点重合),将纸片沿折叠,使点落在点处,延长交于点,则( )
A. B. C. D.不是定值
6.如图,正方形中,点E为中点,连结,将沿翻折得到,连结并延长交于点G,若,则的长为( )
A. B. C. D.
7.如图,在正方形中,是边上的一点,,,将正方形边沿折叠到,延长交于点,连接,,如下4个结论:;②为中点;③;④.其中正确结论的有( )
A.1个 B.2个 C.3个 D.4个
8.如图,在正方形ABCD中,AB=6,点E,F分别在边AB,CD上,∠EFC=120°.若将四边形EBCF沿EF折叠,点B恰好落在AD边上,则AE的长度为( )
A.2 B. C. D.1
9.如图,折叠矩形纸片ABCD,先把△ABF沿AF翻折,点B落在AD边上的点E处,折痕为AF,点F在BC边上,然后将纸片展开铺平,把四边形NCDM翻折,点C恰好落在AE的中点G处,折痕为MN,则( )
A.当点N与点F重合时,∠AFM=90°
B.当GN∥AF时,∠HMG=45°
C.若AB=2,AD=3,则M恰好为DE的中点
D.△GMN的面积有可能为矩形ABCD面积的一半
10.如图.已知正方形的边长为.,将正方形的边沿折叠到,延长交于,连接.现有如下个结论;①;②;③的周长是.其中正确的个数为( )
A. B. C. D.
11.如图,已知在正方形ABCD中,E是BC上一点,将正方形的边CD沿DE折叠到DF,延长EF交AB于点G,连接DG.现有如下4个结论:①AG=GF;②AG与EC一定不相等;③;④的周长是一个定值.其中正确的个数为( )
A.1 B.2 C.3 D.4
12.如图,正方形中,,点E在边上,且.将沿对折至,延长交边于点G,连结、.下列结论:①;②;③;④.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
13.如图,在平面直角坐标系中,四边形OABC是正方形,点A的坐标是(4,0),P为边AB上一点,∠CPB=60°,沿CP折叠正方形OABC,折叠后,点B落在平面内的点B'处,则点B'的坐标为( )
A.(2,) B.(,) C.(2,) D.(,)
14.如图,在边长为6的正方形ABCD中,E是边CD的中点,将沿AE对折至,延长交BC于点G,连接则BG的长( )
A.1 B.2 C. D.3
二、填空题
15.在矩形纸片ABCD中,,点P,Q分别是在边AB,CD上,,将和分别沿PG,EQ翻折,点D,B的对应点分别是,,若四边形是有一边平行于AB的菱形且,则AP的长是____________.
16.如图,将正方形ABCD沿BE对折,使点A落在对角线BD上的A′处,连接A′C,则∠BA′C=________度.
17.如图,已知正方形纸片ABCD,M,N分别是AD、BC的中点,把BC边向上翻折,使点C恰好落在MN上的P点处,BQ为折痕,则∠PBQ=_____度.
18.如图在正方形中,,将沿翻折,使点对应点刚好落在对角线上,将沿翻折,使点对应点落在对角线上,求______.
19.如图,正方形ABCD中,,点E在边CD上,且将沿AE对折至,延长EF交边BC于点G,连接AG、则的面积是______.
20.如图,在正方形纸片 ABCD 中, E 是 CD 的中点,将正方形纸片折叠,点 B 落在线段AE 上的点 G 处,折痕为 AF .若 AD=4 cm,则 CF 的长为___________cm .
21.如图,四边形是一张正方形纸片,其面积为.分别在边,,,上顺次截取,连接,,,.分别以,,,为轴将纸片向内翻折,得到四边形,若四边形的面积为,则__________.
22.如图,将边长为9的正方形纸片ABCD沿MN折叠,使点A落在BC边上点处,点D的对应点为点,若,则DM=__________.
23.如图,将边长为4的正方形纸片ABCD折叠,使得点落在边CD的中点E处,折痕为FG,点F、G分别在边AD、BC上,则折痕FG的长度为_________.
24.如图,正方形ABCD中,AB=6,E是CD的中点,将△ADE沿AE翻折至△AFE,连接CF,则CF的长度是_____.
25.如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB'E,AB'与CD边交于点F,则B'F的长度为_______
26.如图,在正方形ABCD中,BE=EC,将正方形ABCD的边CD沿DE折叠到DF,连接EF、FC、FB,若△DFC的面积为16,则△BEF的面积为_____.
27.如图,正方形ABCD中,AD=+2,已知点E是边AB上的一动点(不与A、B重合)将△ADE沿DE对折,点A的对应点为P,当△APB是等腰三角形时,AE=_____.
28.如图,正方形 中,,是 的中点.将 沿 对折至 , 延长 交 于点 ,则 的长是____.
29.如图,在正方形ABCD中,E是BC边上的一点,BE=4,EC=8,将正方形边AB沿AE折叠到AF,延长EF交DC于G,连接AG,现在有如下四个结论:①∠EAG=45°;②FG=FC;③FC∥AG;④S△GFC=14.其中结论正确的序号是_____.
30.如图,正方形的边长是16,点在边上,,点是边上不与点、重合的一个动点,把沿折叠,点落在处,若恰为等腰三角形,则的长为______.
三、解答题
31.如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
(1)求证:△ABG≌△AFG;
(2)求∠EAG的度数;
(3)求BG的长.
32.如图,在矩形ABCD中,2AB>BC,点E和点F为边AD上两点,将矩形沿着BE和CF折叠,点A和点D恰好重合于矩形内部的点G处,
(1)当AB=BC时,求∠GEF的度数;
(2)若AB=,BC=2,求EF的长.
33.如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.
(1)求证:①△ABG≌△AFG; ②BG=GC;
(2)求△FGC的面积.
34.如图,正方形ABCD中,,点E在CD上,且,将沿AE对折至,延长EF交BC于点G,连接AG、CF.
求证:≌;
求BG的长;
求的面积.
答案
一、单选题
B.C.C.C.B.C.D.A.B.D.C.C.C.B.
二、填空题
15.或3
16.67.5.
17.30.
18.
19.
20.
21.4
22.
23.2.
24.
25.
26.4
27.1或
28.4
29.①③.
30.16或
三、解答题
31.
(1)证明;在正方形ABCD中,AD=AB=BC=CD,∠D=∠B=∠BCD=90°,
∵将△ADE沿AE对折至△AFE,
∴AD=AF,DE=EF,∠D=∠AFE=90°,
∴AB=AF,∠B=∠AFG=90°,
又∵AG=AG,
在Rt△ABG和Rt△AFG中,
,
∴△ABG≌△AFG(HL);
(2)∵△ABG≌△AFG,
∴∠BAG=∠FAG,
∴∠FAG=∠BAF,
由折叠的性质可得:∠EAF=∠DAE,
∴∠EAF=∠DAF,
∴∠EAG=∠EAF+∠FAG=(∠DAF+∠BAF)=∠DAB=×90°=45°;
(3)∵E是CD的中点,
∴DE=CE=CD=×6=3,
设BG=x,则CG=6﹣x,GE=EF+FG=x+3,
∵GE2=CG2+CE2
∴(x+3)2=(6﹣x)2+32,
解得:x=2,
∴BG=2.
32.
解:(1)当AB=BC时,矩形ABCD为正方形,
由折叠得,AB=BG,CD=CG;∠EGB=∠A=90°,
∵AB=BC=CD,
∴BG=BC=GC,
∴∠BGC=60°,
∴∠ABG=30°,
∴∠AEG=150°,
∴∠GEF=30°;
(2)在矩形ABCD中,AB=CD=,
由折叠得,AB=BG,CD=CG,AE=EG,DF=FG,
∴BG=GC=,
又∵BC=2,
得△BGC为等腰直角三角形,且∠GBC=45°,
与(1)同理可得∠FEG=45°,∠EFG=45°,△EGF为等腰直角三角形 ,
设EG=x,则AE=FD=x,EF=,得,
(2+)x=2 ,得x=,
∴EF= .
33.
(1)证明:
①在正方形ABCD中,AD=AB,∠D=∠B=∠C=90
又∵△ADE沿AE对折至△AFE,延长EF交边BC于点G
∴∠AFG=∠AFE=∠D=90 ,AF=AD,
即有∠B=∠AFG=90 ,AB=AF,AG=AG,
∴△ABG≌△AFG
②∵AB=6,点E在边CD上,且CD=3DE,∴DE=FE=2,CE=4
不妨设BG=FG=x,(x>0),则CG=6-x,EG=2+x,
在Rt△CEG中,(2+x)2=42+(6-x)2
解得x=3,于是BG=GC=3
(2)∵,∴
∴S△FGC=S△EGC=
34.是由折叠得到,
,,
又四边形ABCD是正方形,
,,
,,
在和中,
≌,
正方形ABCD中,,,
,
设,则.
在直角中,根据勾股定理,得,
解得.
;
由知,,,
由知,≌,
,
,
由知,,,
,
.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
