九年级数学上册试题 《特殊平行四边形》--菱形最小值问题-北师大版(含答案)
文档属性
| 名称 | 九年级数学上册试题 《特殊平行四边形》--菱形最小值问题-北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 913.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-10 18:15:28 | ||
图片预览




文档简介
《特殊平行四边形》--菱形最小值问题
一、单选题
1.如图,四边形是菱形,对角线,相交于点,,,点是上一动点,点是的中点,则的最小值为( )
A. B. C.3 D.
2.如图,在菱形中,点是对角线上一点,是中点,若菱形周长是16,,则的最小值为( )
A.2 B.2 C.3 D.
3.如图,在菱形中,,,是边的中点,分别是上的动点,连接,则的最小值是( )
A.6 B. C. D.
4.如图,已知菱形,,,E为中点,P为对角线上一点,则的最小值等于( )
A. B. C. D.
5.在菱形ABCD和菱形BEFG中,点A、B、G共线,点C在BE上,∠DAB=60°,AG=8,点M,N分别是AC和EG的中点,则MN的最小值等于( )
A.2 B.4 C.2 D.6
6.如图,在菱形ABCD中,AB=6,∠A=135°,点P是菱形内部一点,且满足,则PC+PD的最小值为( )
A. B. C.6 D.
7.如图,在菱形中,对角线,,点分别是的中点,点在上运动,在运动过程中,存在的最小值,则这个最小值是( )
A.3 B.4 C.5 D.6
8.如图四边形ABCD是菱形,且,是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转得到BN,连接EN、AM、CM,则下列五个结论中正确的是( )
①若菱形ABCD的边长为1,则的最小值1;
②;
③;④连接AN,则;
⑤当的最小值为时,菱形ABCD的边长为2.
A.①②③ B.②④⑤ C.①②⑤ D.②③⑤
9.如图,在菱形中,,,点,,分别是线段,,上的任意一点,则的最小值是( )
A.1 B. C.2 D.
10.如图,在菱形中,,,点是线段上一动点,点是线段上一动点,则的最小值( )
A. B. C. D.
11.如图,点P,Q分别是菱形ABCD的边AD,BC上的两个动点,若线段PQ长的最大值为,最小值为4,则菱形ABCD的边长为( )
A.5 B.10 C. D.8
12.如图,菱形的边长为,,且为的中点,是对角线上的一动点,则的最小值为( )
A. B. C. D.
二、填空题
13.如图,在菱形ABCD中,AB=6,∠A=135°,点P是菱形内部一点,且满足S△PCD=,则PC+PD的最小值是_____.
14.如图,菱形的边长为,且,E是中点,P点在上,则的最小值为_______.
15.如图,在菱形ABCD中,∠DAB=60°,AC=12,P是菱形的对角线AC上的一个动点,M,N分别是菱形ABCD的边AB,BC的中点,则PM+PN的最小值为_____.
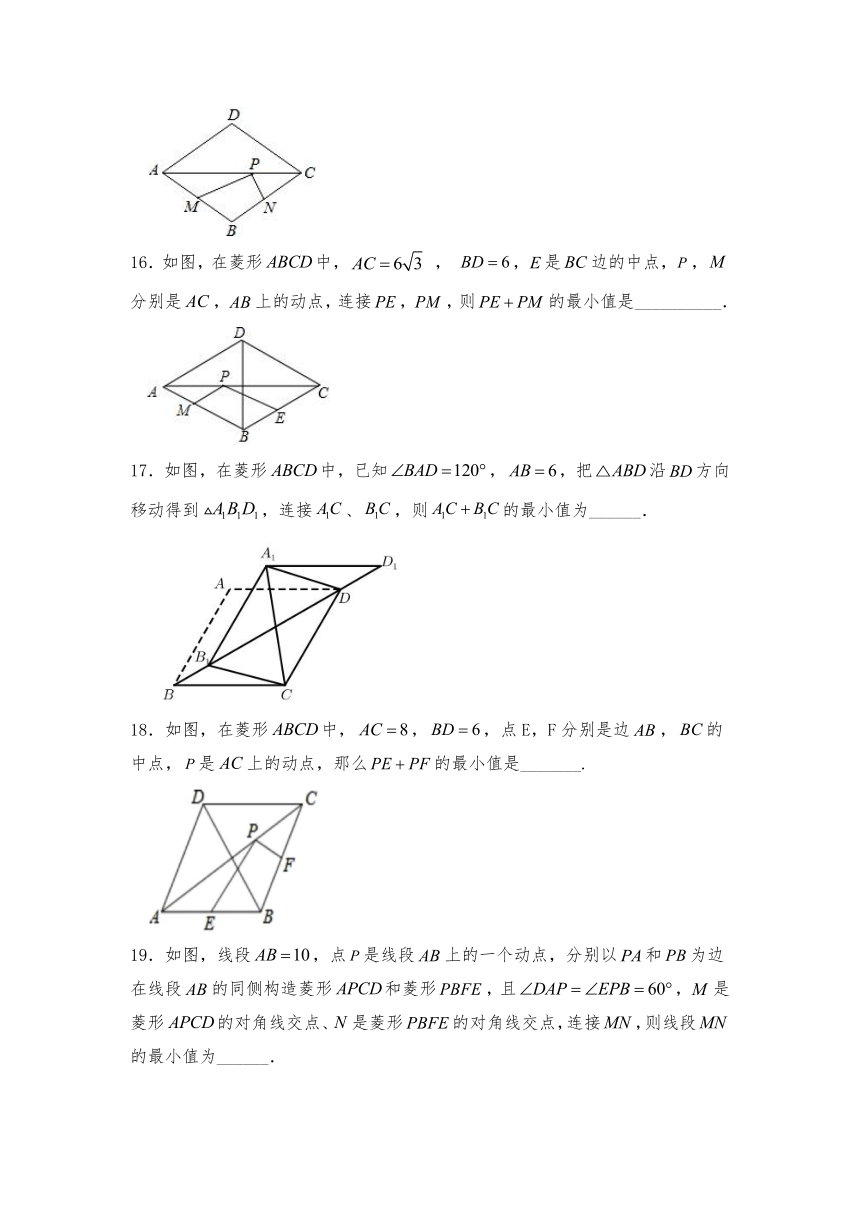
16.如图,在菱形中, , ,是边的中点,,分别是,上的动点,连接,,则的最小值是__________.
17.如图,在菱形中,已知,,把沿方向移动得到,连接、,则的最小值为______.
18.如图,在菱形中,,,点E,F分别是边,的中点,是上的动点,那么的最小值是_______.
19.如图,线段,点是线段上的一个动点,分别以和为边在线段的同侧构造菱形和菱形,且,是菱形的对角线交点、是菱形的对角线交点,连接,则线段的最小值为______.
20.如图,在菱形中,,,点,,分别为线段,,上的任意一点,则的最小值为__________.
21.如图,P、G是菱形ABCD的边BC、DC的中点,K是菱形的对角线BD上的动点,若BD=8,AC=6,则KP+KG的最小值是_____.
22.如图,四边形 是菱形,B=6,且∠ABC=60° ,M是菱形内任一点,连接AM,BM,CM,则AM+BM+CM 的最小值为________.
23.如图,将两张长为8,宽为2的矩形纸条交叉,使重叠部分ABCD是一个菱形。菱形周长的最小值是_________,菱形周长最大值是_________.
24.如图,在边长为的菱形中,,是边的中点,是对角线上的动点,连接,,则的最小值______.
25.如图,在菱形中,,,点是边的中点,点、分别是、上的两个动点,则的最小值是_________.
26.如图,菱形的边长为1, .分别是上的动点,且,则的最小值为_______.
27.如图,在中,,点D、E、F分别在、、上,且四边形为菱形,则菱形的边长为_____;若点P是上一个动点,则的最小值为_____.
28.如图,点P,Q分别是菱形的边、上的两个动点,若线段长的最大值为,最小值为8,则菱形的边长为________.
29.已知菱形中,,,边上有点点两动点,始终保持,连接取中点并连接则的最小值是_______.
30.如图,在菱形中,,,点P,M分别是边和对角线上的动点,则的最小值为_________.
31.在菱形中,,点是的中点,是对角线上的一个动点,则的最小值为_______.
32.菱形中,,,为的中点,点是对角线上一动点,连接,则的周长的最小值为_________.
33.在菱形ABCD中,∠C=∠EDF=60°,AB=1,现将∠EDF绕点D任意旋转,分别交边AB、BC于点E、F(不与菱形的顶点重合),连接EF,则△BEF的周长最小值是_____.
34.如图,在菱形中,,点P为的中点,分别为线段上的任意一点,则的最小值为______.
35.如图,四边形是菱形,点分别在边上,其中是对角线上的动点,若的最小值为,则该菱形的面积为____________
36.如图,在菱形中,,.、分别是线段、上的任意一点,则的最小值为________.
三、解答题
37.如图,在菱形中,,,为上一动点,为中点.
(1)求菱形的面积;
(2)求的最小值.
38.在菱形中,,,点是线段上的一个动点.
(1)如图①,求的最小值.
(2)如图②,若也是边上的一个动点,且,求的最小值.
(3)如图③,若,则在菱形内部存在一点,使得点分别到点、点、边的距离之和最小.请你画出这样的点,并求出这个最小值.
39.在菱形中,,点是对角线上一动点,将线段绕点顺时针旋转120°到,连接,连接并延长,分别交于点.
(1)求证:;
(2)已知,若的最小值为,求菱形的面积.
40.如图,菱形ABCD中,AB=2,∠A=120°,点P、Q、K分别为线段BC、CD、BD上的任意一点,求PK+QK的最小值.
41.如图,在菱形ABCD中,点 E、F分别为边 AD、CD上的动点(都与菱形的顶点不重合),联结 EF、BE、BF .
(1)若∠A=60°,且 AE+CF=AB,判断△BEF 的形状,并说明理由;
(2)在(1)的条件下,设菱形的边长为a,求△BEF面积的最小值.
42.如图,在菱形ABCD中,∠ABC=120°,点E是边AB的中点,P是对角线AC上的一个动点,若AB=2,求PB+PE的最小值是多少?
答案
一、单选题
A.A.D.B.A.B.C.C.B.D.A.D.
二、填空题
13.
14.
15.4
16.
17.
18.5
19.
20.
21.5
22.
23.8 17
24.
25.
26.
27.2
28.10
29.3
30.3
31.
32.
33.1 +
34.
35.36
36.
37.(1);(2).
三、解答题
37.解:(1)如答图,连接,,
∵四边形是菱形,
∴,
又∵,
∴是等边三角形,
∵为中点.
∴,.
在中,.
∴.
(2)如答图,连接,
∵四边形为菱形,
∴点与点关于对称.
∴.
∴.
当点、、在一条线段上时,取值最小.
即时,取得最小值.
38.()根据垂线段最短,当时,最小,最小为菱形的高.
()连接、、,
在菱形中,可证为等边三角形,
的最小值即为的最小值.
()如图,以为边在菱形外作等边,
作于,即为点分别到点、点、边的距离之和最小,
当于时,点即为所求.理由如下:
当绕点逆时针旋转得到,点在上,
此时,,,
要使点分别到点、点、边的距离之和最小,
则要即可.
作,
由题意可得:为的中点.
在中,,,
∴,,
∴.
39.(1)证明:四边形是菱形,且,
∴,
∴,
由旋转的性质得:
∴,
∴;
(2)连接AC,
∵四边形ABCD是菱形,
∴AB=BC,
∵,
∴△ABC是等边三角形,
∴AB=BC,
∵,
∴,
∴,
∴当时,最小,此时最小,
∵MN=,
∴PC=2,
∵∠DBC=,∠BPC=90°,
∴BC=2PC=4,
∴菱形的面积
40.
解:∵四边形ABCD是菱形,
∴,AD∥BC,
如图2,作点Q关于直线BD的对称点为,
∴,
∴,
∵在中,PK+QK总是大于的,
∴如图3,当点K落在上时,PK+QK的最小值为,
∴根据点到直线,垂线段最短可得:如图4,的最小值为,就是菱形ABCD的高,
过点A作AE⊥BC于点E,如图4所示,
∵AB=2,
∴BE=1,
∴在中,,
∴=.
41.解:(1)△BEF的形状为等边三角形.证明如下:
如图,在菱形ABCD中,∠A=60°,∴AB∥DC,AB=BC=CD=DA,∴∠ADC=120°,∴∠1=∠2=60°,∴∠ABD=∠1=∠A=60°,∴AB=BD,∠A=∠2.
∵AE+CF=AB,DF+CF=CD,∴AE=DF,∴△ABE≌△DBF,∴BE=BF,∠3=∠4.
又∵∠3+∠5=60°,∴∠4+∠5=60°,∴△BEF为等边三角形.
(2)如图,当BE⊥AD时,BE最小,此时,S△BEF最小.
设此时EF与BD交于点M,∴∠ABE=∠DBE=30°.
∵∠BEM=60°,∴∠BME=90°.
在Rt△ABE中,AB=a,∴.
在Rt△BEM中,∠BEM=60°,∴.
∴.
42.
解:如图,连接PD,BD,
∵四边形ABCD是菱形,
∴对角线AC与BD互相垂直平分,
∴AC是BD的垂直平分线,
∴,
∴,
由两点之间线段最短可知,当点D,P,E在同一直线上时,取得最小值,最小值等于线段DE的长,
即的最小值为线段DE的长,
∵四边形ABCD是菱形,,,
∴,
∴是等边三角形,
又∵点E是AB的中点,
∴,
∴在中,,
故的最小值是3.
一、单选题
1.如图,四边形是菱形,对角线,相交于点,,,点是上一动点,点是的中点,则的最小值为( )
A. B. C.3 D.
2.如图,在菱形中,点是对角线上一点,是中点,若菱形周长是16,,则的最小值为( )
A.2 B.2 C.3 D.
3.如图,在菱形中,,,是边的中点,分别是上的动点,连接,则的最小值是( )
A.6 B. C. D.
4.如图,已知菱形,,,E为中点,P为对角线上一点,则的最小值等于( )
A. B. C. D.
5.在菱形ABCD和菱形BEFG中,点A、B、G共线,点C在BE上,∠DAB=60°,AG=8,点M,N分别是AC和EG的中点,则MN的最小值等于( )
A.2 B.4 C.2 D.6
6.如图,在菱形ABCD中,AB=6,∠A=135°,点P是菱形内部一点,且满足,则PC+PD的最小值为( )
A. B. C.6 D.
7.如图,在菱形中,对角线,,点分别是的中点,点在上运动,在运动过程中,存在的最小值,则这个最小值是( )
A.3 B.4 C.5 D.6
8.如图四边形ABCD是菱形,且,是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转得到BN,连接EN、AM、CM,则下列五个结论中正确的是( )
①若菱形ABCD的边长为1,则的最小值1;
②;
③;④连接AN,则;
⑤当的最小值为时,菱形ABCD的边长为2.
A.①②③ B.②④⑤ C.①②⑤ D.②③⑤
9.如图,在菱形中,,,点,,分别是线段,,上的任意一点,则的最小值是( )
A.1 B. C.2 D.
10.如图,在菱形中,,,点是线段上一动点,点是线段上一动点,则的最小值( )
A. B. C. D.
11.如图,点P,Q分别是菱形ABCD的边AD,BC上的两个动点,若线段PQ长的最大值为,最小值为4,则菱形ABCD的边长为( )
A.5 B.10 C. D.8
12.如图,菱形的边长为,,且为的中点,是对角线上的一动点,则的最小值为( )
A. B. C. D.
二、填空题
13.如图,在菱形ABCD中,AB=6,∠A=135°,点P是菱形内部一点,且满足S△PCD=,则PC+PD的最小值是_____.
14.如图,菱形的边长为,且,E是中点,P点在上,则的最小值为_______.
15.如图,在菱形ABCD中,∠DAB=60°,AC=12,P是菱形的对角线AC上的一个动点,M,N分别是菱形ABCD的边AB,BC的中点,则PM+PN的最小值为_____.
16.如图,在菱形中, , ,是边的中点,,分别是,上的动点,连接,,则的最小值是__________.
17.如图,在菱形中,已知,,把沿方向移动得到,连接、,则的最小值为______.
18.如图,在菱形中,,,点E,F分别是边,的中点,是上的动点,那么的最小值是_______.
19.如图,线段,点是线段上的一个动点,分别以和为边在线段的同侧构造菱形和菱形,且,是菱形的对角线交点、是菱形的对角线交点,连接,则线段的最小值为______.
20.如图,在菱形中,,,点,,分别为线段,,上的任意一点,则的最小值为__________.
21.如图,P、G是菱形ABCD的边BC、DC的中点,K是菱形的对角线BD上的动点,若BD=8,AC=6,则KP+KG的最小值是_____.
22.如图,四边形 是菱形,B=6,且∠ABC=60° ,M是菱形内任一点,连接AM,BM,CM,则AM+BM+CM 的最小值为________.
23.如图,将两张长为8,宽为2的矩形纸条交叉,使重叠部分ABCD是一个菱形。菱形周长的最小值是_________,菱形周长最大值是_________.
24.如图,在边长为的菱形中,,是边的中点,是对角线上的动点,连接,,则的最小值______.
25.如图,在菱形中,,,点是边的中点,点、分别是、上的两个动点,则的最小值是_________.
26.如图,菱形的边长为1, .分别是上的动点,且,则的最小值为_______.
27.如图,在中,,点D、E、F分别在、、上,且四边形为菱形,则菱形的边长为_____;若点P是上一个动点,则的最小值为_____.
28.如图,点P,Q分别是菱形的边、上的两个动点,若线段长的最大值为,最小值为8,则菱形的边长为________.
29.已知菱形中,,,边上有点点两动点,始终保持,连接取中点并连接则的最小值是_______.
30.如图,在菱形中,,,点P,M分别是边和对角线上的动点,则的最小值为_________.
31.在菱形中,,点是的中点,是对角线上的一个动点,则的最小值为_______.
32.菱形中,,,为的中点,点是对角线上一动点,连接,则的周长的最小值为_________.
33.在菱形ABCD中,∠C=∠EDF=60°,AB=1,现将∠EDF绕点D任意旋转,分别交边AB、BC于点E、F(不与菱形的顶点重合),连接EF,则△BEF的周长最小值是_____.
34.如图,在菱形中,,点P为的中点,分别为线段上的任意一点,则的最小值为______.
35.如图,四边形是菱形,点分别在边上,其中是对角线上的动点,若的最小值为,则该菱形的面积为____________
36.如图,在菱形中,,.、分别是线段、上的任意一点,则的最小值为________.
三、解答题
37.如图,在菱形中,,,为上一动点,为中点.
(1)求菱形的面积;
(2)求的最小值.
38.在菱形中,,,点是线段上的一个动点.
(1)如图①,求的最小值.
(2)如图②,若也是边上的一个动点,且,求的最小值.
(3)如图③,若,则在菱形内部存在一点,使得点分别到点、点、边的距离之和最小.请你画出这样的点,并求出这个最小值.
39.在菱形中,,点是对角线上一动点,将线段绕点顺时针旋转120°到,连接,连接并延长,分别交于点.
(1)求证:;
(2)已知,若的最小值为,求菱形的面积.
40.如图,菱形ABCD中,AB=2,∠A=120°,点P、Q、K分别为线段BC、CD、BD上的任意一点,求PK+QK的最小值.
41.如图,在菱形ABCD中,点 E、F分别为边 AD、CD上的动点(都与菱形的顶点不重合),联结 EF、BE、BF .
(1)若∠A=60°,且 AE+CF=AB,判断△BEF 的形状,并说明理由;
(2)在(1)的条件下,设菱形的边长为a,求△BEF面积的最小值.
42.如图,在菱形ABCD中,∠ABC=120°,点E是边AB的中点,P是对角线AC上的一个动点,若AB=2,求PB+PE的最小值是多少?
答案
一、单选题
A.A.D.B.A.B.C.C.B.D.A.D.
二、填空题
13.
14.
15.4
16.
17.
18.5
19.
20.
21.5
22.
23.8 17
24.
25.
26.
27.2
28.10
29.3
30.3
31.
32.
33.1 +
34.
35.36
36.
37.(1);(2).
三、解答题
37.解:(1)如答图,连接,,
∵四边形是菱形,
∴,
又∵,
∴是等边三角形,
∵为中点.
∴,.
在中,.
∴.
(2)如答图,连接,
∵四边形为菱形,
∴点与点关于对称.
∴.
∴.
当点、、在一条线段上时,取值最小.
即时,取得最小值.
38.()根据垂线段最短,当时,最小,最小为菱形的高.
()连接、、,
在菱形中,可证为等边三角形,
的最小值即为的最小值.
()如图,以为边在菱形外作等边,
作于,即为点分别到点、点、边的距离之和最小,
当于时,点即为所求.理由如下:
当绕点逆时针旋转得到,点在上,
此时,,,
要使点分别到点、点、边的距离之和最小,
则要即可.
作,
由题意可得:为的中点.
在中,,,
∴,,
∴.
39.(1)证明:四边形是菱形,且,
∴,
∴,
由旋转的性质得:
∴,
∴;
(2)连接AC,
∵四边形ABCD是菱形,
∴AB=BC,
∵,
∴△ABC是等边三角形,
∴AB=BC,
∵,
∴,
∴,
∴当时,最小,此时最小,
∵MN=,
∴PC=2,
∵∠DBC=,∠BPC=90°,
∴BC=2PC=4,
∴菱形的面积
40.
解:∵四边形ABCD是菱形,
∴,AD∥BC,
如图2,作点Q关于直线BD的对称点为,
∴,
∴,
∵在中,PK+QK总是大于的,
∴如图3,当点K落在上时,PK+QK的最小值为,
∴根据点到直线,垂线段最短可得:如图4,的最小值为,就是菱形ABCD的高,
过点A作AE⊥BC于点E,如图4所示,
∵AB=2,
∴BE=1,
∴在中,,
∴=.
41.解:(1)△BEF的形状为等边三角形.证明如下:
如图,在菱形ABCD中,∠A=60°,∴AB∥DC,AB=BC=CD=DA,∴∠ADC=120°,∴∠1=∠2=60°,∴∠ABD=∠1=∠A=60°,∴AB=BD,∠A=∠2.
∵AE+CF=AB,DF+CF=CD,∴AE=DF,∴△ABE≌△DBF,∴BE=BF,∠3=∠4.
又∵∠3+∠5=60°,∴∠4+∠5=60°,∴△BEF为等边三角形.
(2)如图,当BE⊥AD时,BE最小,此时,S△BEF最小.
设此时EF与BD交于点M,∴∠ABE=∠DBE=30°.
∵∠BEM=60°,∴∠BME=90°.
在Rt△ABE中,AB=a,∴.
在Rt△BEM中,∠BEM=60°,∴.
∴.
42.
解:如图,连接PD,BD,
∵四边形ABCD是菱形,
∴对角线AC与BD互相垂直平分,
∴AC是BD的垂直平分线,
∴,
∴,
由两点之间线段最短可知,当点D,P,E在同一直线上时,取得最小值,最小值等于线段DE的长,
即的最小值为线段DE的长,
∵四边形ABCD是菱形,,,
∴,
∴是等边三角形,
又∵点E是AB的中点,
∴,
∴在中,,
故的最小值是3.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
