九年级数学上册试题 4.2 平行线分线段成比例同步练习-北师大版(含答案)
文档属性
| 名称 | 九年级数学上册试题 4.2 平行线分线段成比例同步练习-北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 520.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-10 18:23:08 | ||
图片预览



文档简介
4.2 平行线分线段成比例
一、单选题
1.如图,已知,那么下列结论正确的是( )
A. B. C. D.
2.如图,△ABC中,点D、E分别在边AB、BC上,DE∥AC,若DB=4,AB=6,BE=3,则EC的长是( )
A.4 B.2 C. D.
3.如图,E是 ABCD的边AD上的一点,连接BE并延长,交CD的延长线于点F,若AE: BC =3: 5,则FD: DC的值为( )
A.2 : 3 B.2:5 C.3 : 4 D.3 : 5
4.如果用线段a、b、c,求作线段x,使,那么下列作图正确的是( )
A. B.
C. D.
5.如图,AD是△ABC的中线,E是AC边上一点,且CE:AE=1:2,BE交AD于点F,则AF:FD为( )
A.5:1 B.4:1 C.3:1 D.2:1
6.如图,在△ABC中,AB=4,AC=3,AD平分∠BAC,则S△ABD:S△ADC为( )
A.4:3 B.16:19 C.3:4 D.不能确定
7.如图,E,F是平行四边形ABCD对角线BD上的两点,DE=EF=BF,连接CE并延长交AD于点G,连接CF并延长交AB于点H,连接CH,设△CDG的面积为S1,△CHG的面积为S2,则S1与S2的关系正确的是( )
A. B. C. D.
8.小明的数学作业本的纸上都是等距离的横线,他在上面任意画一条不与这些横线平行的直线,那么这条直线被这些横线所截得的线段( )
A.平行 B.相等 C.平行或相等 D.不相等
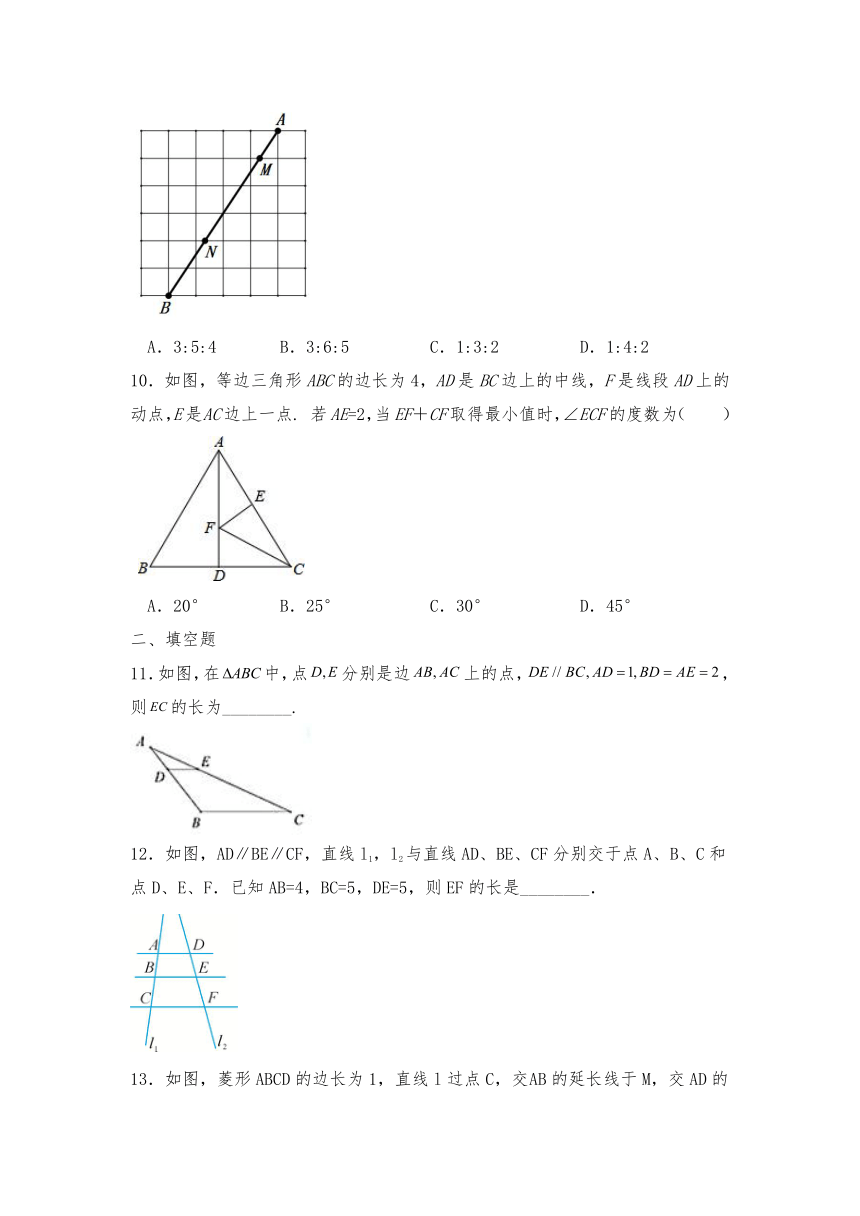
9.如图,在6×6的正方形网格中,联结小正方形中两个顶点A、B,如果线段AB与网格线的其中两个交点为M、N,那么AM:MN:NB的值是( )
A.3:5:4 B.3:6:5 C.1:3:2 D.1:4:2
10.如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是线段AD上的动点,E是AC边上一点. 若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )
A.20° B.25° C.30° D.45°
二、填空题
11.如图,在中,点分别是边上的点,, 则的长为________.
12.如图,AD∥BE∥CF,直线l1,l2与直线AD、BE、CF分别交于点A、B、C和点D、E、F.已知AB=4,BC=5,DE=5,则EF的长是________.
13.如图,菱形ABCD的边长为1,直线l过点C,交AB的延长线于M,交AD的延长线于N,则=____.
14.如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE// BC,EF//AB,且AD:DB=3:5,那么CF:CB 等于__________.
15.如图,在△ABC中,D,E两点分别在AB,AC边上,DE∥BC.如果,AC=10,那么EC=________.
16.如图,在中,点E、D在边AC上,点F、M在边AB上,且,,如果FD的延长线交BC的延长线于N,那么的值为______.
17.已知中,分别是直线和上的点,若且,则_________.
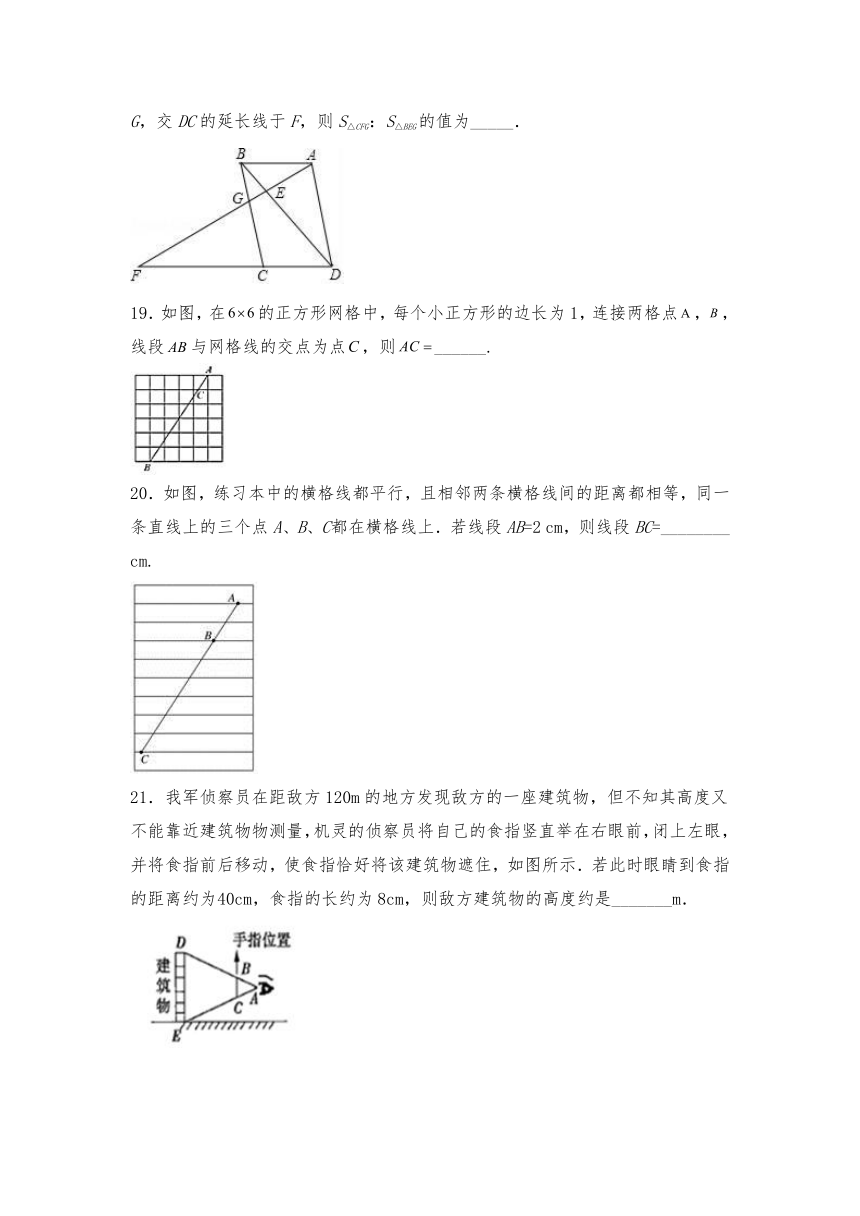
18.如图,在 ABCD的对角线BD上取一点E.使得BE=BD,延长AE交BC于G,交DC的延长线于F,则S△CFG:S△BEG的值为_____.
19.如图,在的正方形网格中,每个小正方形的边长为1,连接两格点,,线段与网格线的交点为点,则______.
20.如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A、B、C都在横格线上.若线段AB=2 cm,则线段BC=________ cm.
21.我军侦察员在距敌方120m的地方发现敌方的一座建筑物,但不知其高度又不能靠近建筑物物测量,机灵的侦察员将自己的食指竖直举在右眼前,闭上左眼,并将食指前后移动,使食指恰好将该建筑物遮住,如图所示.若此时眼睛到食指的距离约为40cm,食指的长约为8cm,则敌方建筑物的高度约是_______m.
22.如图,在等腰中,,点是底边上一个动点, 分别是、的中点.若的最小值是2,则周长是_________.
三、解答题
23.如图,l1∥l2∥l3,AB=3,AD=2,DE=4,EF=7.5,求BC、BF的长.
24.如图,△ABC中,已知MN∥BC,DN∥MC,求证:AM2=AB AD.
25.如图,在△ABC中,DE∥AC,DF∥AE,BD:DA=3:2,BF=6,DF=8,
(1)求EF的长;(2)求EA的长.
26.如图,已知DE∥BC,FE∥CD,AF=3,AD=5,AE=4.
(1)求CE的长;
(2)求AB的长.
27.如图,在△ABC中,BD、CE分别是AC、AB上的中线,BD与CE相交于点O.
(1)利用尺规作图取线段CO的中点.(保留作图痕迹,不写作法);
(2)猜想CO与OE的长度有什么关系,并说明理由.
28.如图,已知点F在AB上,且AF:BF=1:2,点D是BC延长线上一点,BC:CD=2:1,连接FD与AC交于点N,求FN:ND的值.
29.如图,在中,D为AC上一点,E为CB的延长线上一点,连接BD交AB于点F,且,.求证:.
30.如图,在Rt△ABC中,∠ACB = 90°,BC = 6,AC = 8.点D是AB边上一点,过点D作DE // BC,交边AC于E.过点C作CF // AB,交DE的延长线于点F.
(1)如果,求线段EF的长;
(2)求∠CFE的正弦值.
31.已知,如图,AB、DE是直立在地面上的两根立柱,AB=12m,某一时刻AB在阳光下的投影BC=4m.
(1)请你在图中画出此时DE在阳光下的投影.
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长6m,请你计算DE的长.
32.在的方格纸中,点都在格点上,按要求画图:
在图1中找-一个格点,使以点为顶点的四边形是平行四边形.
在图2中仅用无刻度的直尺,把线段分成两部分,使得这两部分长度之比为(保留画图痕迹,不写画法).
答案
一、单选题
C.C.A.B.B.A.C.B.C.C.
二、填空题
11.4.
12.
13.1.
14.5:8
15.4
16.
17.4或8
18.16
19.
20.6
21.24
22.
三、解答题
23.∵l1∥l2∥l3,
∴,
∵AB=3,AD=2,DE=4,
∴,
解得:BC=6,
∵l1∥l2∥l3,
∵AB=3,AD=2,DE=4,EF=7.5,
∴,
∴,
解得:BF=2.5.
24.证明:∵MN∥BC,
∴,
∵DN∥MC,
∴,
∴,
即AM2=AD AB.
25.解:(1)∵DF∥AE,
∴=,即=,
解得,EF=4;
(2)∵DF∥AE,
∴=,即=,
解得,EA=.
26.解:(1)∵FE∥CD,
∴=,即=,
解得,AC=,
则CE=AC﹣AE=﹣4=;
(2)∵DE∥BC,
∴=,即=,
解得,AB=.
27.解:(1)如图,点即为所求;
(2).
理由:连接.如图,
、分别是、上的中线,
为的中位线,
,,
,
.
28.解:过点F作FE∥BD,交AC于点E,
∴,
∵AF:BF=1:2,
∴=,
∴,
即FE=BC,
∵BC:CD=2:1,
∴CD=BC,
∵FE∥BD,
∴.
即FN:ND=2:3.
29.∵,∴,,∵,∴,∴.
30.解:(1)∵ DE // BC,∴ .
又∵ BC = 6,∴ DE = 2.
∵ DF // BC,CF // AB,∴ 四边形BCFD是平行四边形.
∴ DF = BC = 6.∴ EF = DF – DE = 4.
(2)∵ 四边形BCFD是平行四边形, ∴ ∠B =∠F.
在Rt△ABC中,∠ACB = 90°,BC = 6,AC = 8,
利用勾股定理,得.
∴ .∴ .
31.解:(1)如图所示:
EM即为所求;
(2)∵AB=12m,某一时刻AB在阳光下的投影BC=4m,
DE在阳光下的投影长6m,
∴设DE的长为xm,
则 ,
解得:x=18,
答:DE的长18米.
32.解:(1)平行四边形ABCD如图1所示:
(2)如图2所示,取格点E,F连EF,线段EF把线段AB分成1:2;
或取格点G,H连GH,线段GH把线段AB分成1:2.
一、单选题
1.如图,已知,那么下列结论正确的是( )
A. B. C. D.
2.如图,△ABC中,点D、E分别在边AB、BC上,DE∥AC,若DB=4,AB=6,BE=3,则EC的长是( )
A.4 B.2 C. D.
3.如图,E是 ABCD的边AD上的一点,连接BE并延长,交CD的延长线于点F,若AE: BC =3: 5,则FD: DC的值为( )
A.2 : 3 B.2:5 C.3 : 4 D.3 : 5
4.如果用线段a、b、c,求作线段x,使,那么下列作图正确的是( )
A. B.
C. D.
5.如图,AD是△ABC的中线,E是AC边上一点,且CE:AE=1:2,BE交AD于点F,则AF:FD为( )
A.5:1 B.4:1 C.3:1 D.2:1
6.如图,在△ABC中,AB=4,AC=3,AD平分∠BAC,则S△ABD:S△ADC为( )
A.4:3 B.16:19 C.3:4 D.不能确定
7.如图,E,F是平行四边形ABCD对角线BD上的两点,DE=EF=BF,连接CE并延长交AD于点G,连接CF并延长交AB于点H,连接CH,设△CDG的面积为S1,△CHG的面积为S2,则S1与S2的关系正确的是( )
A. B. C. D.
8.小明的数学作业本的纸上都是等距离的横线,他在上面任意画一条不与这些横线平行的直线,那么这条直线被这些横线所截得的线段( )
A.平行 B.相等 C.平行或相等 D.不相等
9.如图,在6×6的正方形网格中,联结小正方形中两个顶点A、B,如果线段AB与网格线的其中两个交点为M、N,那么AM:MN:NB的值是( )
A.3:5:4 B.3:6:5 C.1:3:2 D.1:4:2
10.如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是线段AD上的动点,E是AC边上一点. 若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )
A.20° B.25° C.30° D.45°
二、填空题
11.如图,在中,点分别是边上的点,, 则的长为________.
12.如图,AD∥BE∥CF,直线l1,l2与直线AD、BE、CF分别交于点A、B、C和点D、E、F.已知AB=4,BC=5,DE=5,则EF的长是________.
13.如图,菱形ABCD的边长为1,直线l过点C,交AB的延长线于M,交AD的延长线于N,则=____.
14.如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE// BC,EF//AB,且AD:DB=3:5,那么CF:CB 等于__________.
15.如图,在△ABC中,D,E两点分别在AB,AC边上,DE∥BC.如果,AC=10,那么EC=________.
16.如图,在中,点E、D在边AC上,点F、M在边AB上,且,,如果FD的延长线交BC的延长线于N,那么的值为______.
17.已知中,分别是直线和上的点,若且,则_________.
18.如图,在 ABCD的对角线BD上取一点E.使得BE=BD,延长AE交BC于G,交DC的延长线于F,则S△CFG:S△BEG的值为_____.
19.如图,在的正方形网格中,每个小正方形的边长为1,连接两格点,,线段与网格线的交点为点,则______.
20.如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A、B、C都在横格线上.若线段AB=2 cm,则线段BC=________ cm.
21.我军侦察员在距敌方120m的地方发现敌方的一座建筑物,但不知其高度又不能靠近建筑物物测量,机灵的侦察员将自己的食指竖直举在右眼前,闭上左眼,并将食指前后移动,使食指恰好将该建筑物遮住,如图所示.若此时眼睛到食指的距离约为40cm,食指的长约为8cm,则敌方建筑物的高度约是_______m.
22.如图,在等腰中,,点是底边上一个动点, 分别是、的中点.若的最小值是2,则周长是_________.
三、解答题
23.如图,l1∥l2∥l3,AB=3,AD=2,DE=4,EF=7.5,求BC、BF的长.
24.如图,△ABC中,已知MN∥BC,DN∥MC,求证:AM2=AB AD.
25.如图,在△ABC中,DE∥AC,DF∥AE,BD:DA=3:2,BF=6,DF=8,
(1)求EF的长;(2)求EA的长.
26.如图,已知DE∥BC,FE∥CD,AF=3,AD=5,AE=4.
(1)求CE的长;
(2)求AB的长.
27.如图,在△ABC中,BD、CE分别是AC、AB上的中线,BD与CE相交于点O.
(1)利用尺规作图取线段CO的中点.(保留作图痕迹,不写作法);
(2)猜想CO与OE的长度有什么关系,并说明理由.
28.如图,已知点F在AB上,且AF:BF=1:2,点D是BC延长线上一点,BC:CD=2:1,连接FD与AC交于点N,求FN:ND的值.
29.如图,在中,D为AC上一点,E为CB的延长线上一点,连接BD交AB于点F,且,.求证:.
30.如图,在Rt△ABC中,∠ACB = 90°,BC = 6,AC = 8.点D是AB边上一点,过点D作DE // BC,交边AC于E.过点C作CF // AB,交DE的延长线于点F.
(1)如果,求线段EF的长;
(2)求∠CFE的正弦值.
31.已知,如图,AB、DE是直立在地面上的两根立柱,AB=12m,某一时刻AB在阳光下的投影BC=4m.
(1)请你在图中画出此时DE在阳光下的投影.
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长6m,请你计算DE的长.
32.在的方格纸中,点都在格点上,按要求画图:
在图1中找-一个格点,使以点为顶点的四边形是平行四边形.
在图2中仅用无刻度的直尺,把线段分成两部分,使得这两部分长度之比为(保留画图痕迹,不写画法).
答案
一、单选题
C.C.A.B.B.A.C.B.C.C.
二、填空题
11.4.
12.
13.1.
14.5:8
15.4
16.
17.4或8
18.16
19.
20.6
21.24
22.
三、解答题
23.∵l1∥l2∥l3,
∴,
∵AB=3,AD=2,DE=4,
∴,
解得:BC=6,
∵l1∥l2∥l3,
∵AB=3,AD=2,DE=4,EF=7.5,
∴,
∴,
解得:BF=2.5.
24.证明:∵MN∥BC,
∴,
∵DN∥MC,
∴,
∴,
即AM2=AD AB.
25.解:(1)∵DF∥AE,
∴=,即=,
解得,EF=4;
(2)∵DF∥AE,
∴=,即=,
解得,EA=.
26.解:(1)∵FE∥CD,
∴=,即=,
解得,AC=,
则CE=AC﹣AE=﹣4=;
(2)∵DE∥BC,
∴=,即=,
解得,AB=.
27.解:(1)如图,点即为所求;
(2).
理由:连接.如图,
、分别是、上的中线,
为的中位线,
,,
,
.
28.解:过点F作FE∥BD,交AC于点E,
∴,
∵AF:BF=1:2,
∴=,
∴,
即FE=BC,
∵BC:CD=2:1,
∴CD=BC,
∵FE∥BD,
∴.
即FN:ND=2:3.
29.∵,∴,,∵,∴,∴.
30.解:(1)∵ DE // BC,∴ .
又∵ BC = 6,∴ DE = 2.
∵ DF // BC,CF // AB,∴ 四边形BCFD是平行四边形.
∴ DF = BC = 6.∴ EF = DF – DE = 4.
(2)∵ 四边形BCFD是平行四边形, ∴ ∠B =∠F.
在Rt△ABC中,∠ACB = 90°,BC = 6,AC = 8,
利用勾股定理,得.
∴ .∴ .
31.解:(1)如图所示:
EM即为所求;
(2)∵AB=12m,某一时刻AB在阳光下的投影BC=4m,
DE在阳光下的投影长6m,
∴设DE的长为xm,
则 ,
解得:x=18,
答:DE的长18米.
32.解:(1)平行四边形ABCD如图1所示:
(2)如图2所示,取格点E,F连EF,线段EF把线段AB分成1:2;
或取格点G,H连GH,线段GH把线段AB分成1:2.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
