九年级数学上册试题 4.7 相似三角形的性质-北师大版(含答案)
文档属性
| 名称 | 九年级数学上册试题 4.7 相似三角形的性质-北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 571.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-10 18:25:52 | ||
图片预览

文档简介
4.7 相似三角形的性质
一、单选题
1.如图,在中,点D和E分别是边和的中点,连接,与交于点O,若的面积为1,则的面积为( )
A.6 B.9 C.12 D.13.5
2.如图,直角三角板中,,一边平行于的直尺将三角板分成面积相等的三部分.若,则的长为( )
A. B. C. D.
3.如图,在矩形ABCD中,AB=3,BC=4,点E是边BC的中点,连接AE,与对角线BD交于点F.点M是AD边上的一个动点,连接MF、MC,则MF+MC的最小值为( )
A. B.4 C. D.5
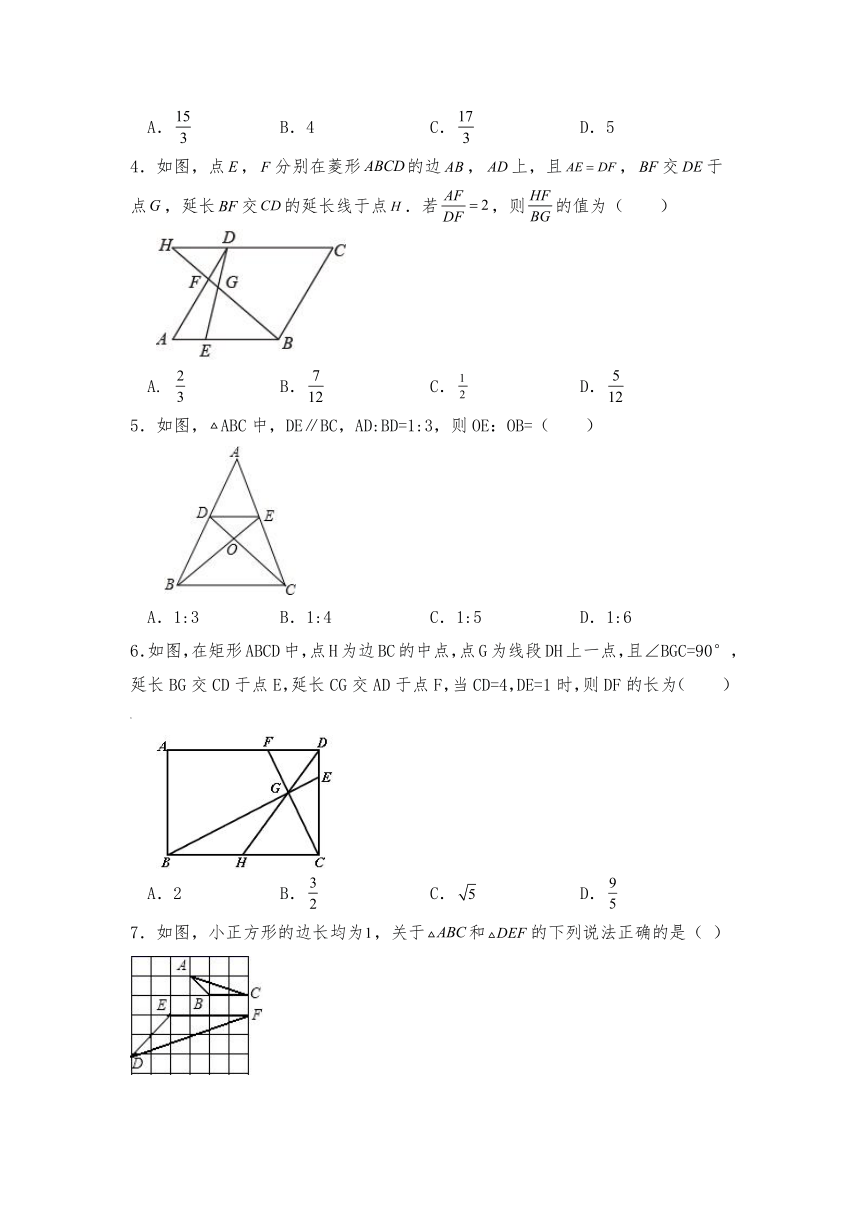
4.如图,点,分别在菱形的边,上,且,交于点,延长交的延长线于点.若,则的值为( )
A. B. C. D.
5.如图,ABC中,DE∥BC,AD:BD=1:3,则OE:OB=( )
A.1:3 B.1:4 C.1:5 D.1:6
6.如图,在矩形ABCD中,点H为边BC的中点,点G为线段DH上一点,且∠BGC=90°,延长BG交CD于点E,延长CG交AD于点F,当CD=4,DE=1时,则DF的长为( )
A.2 B. C. D.
7.如图,小正方形的边长均为,关于和的下列说法正确的是( )
A.和一定不相似 B.和是位似图形
C.和相似且相似比是 D.和相似且相似比是
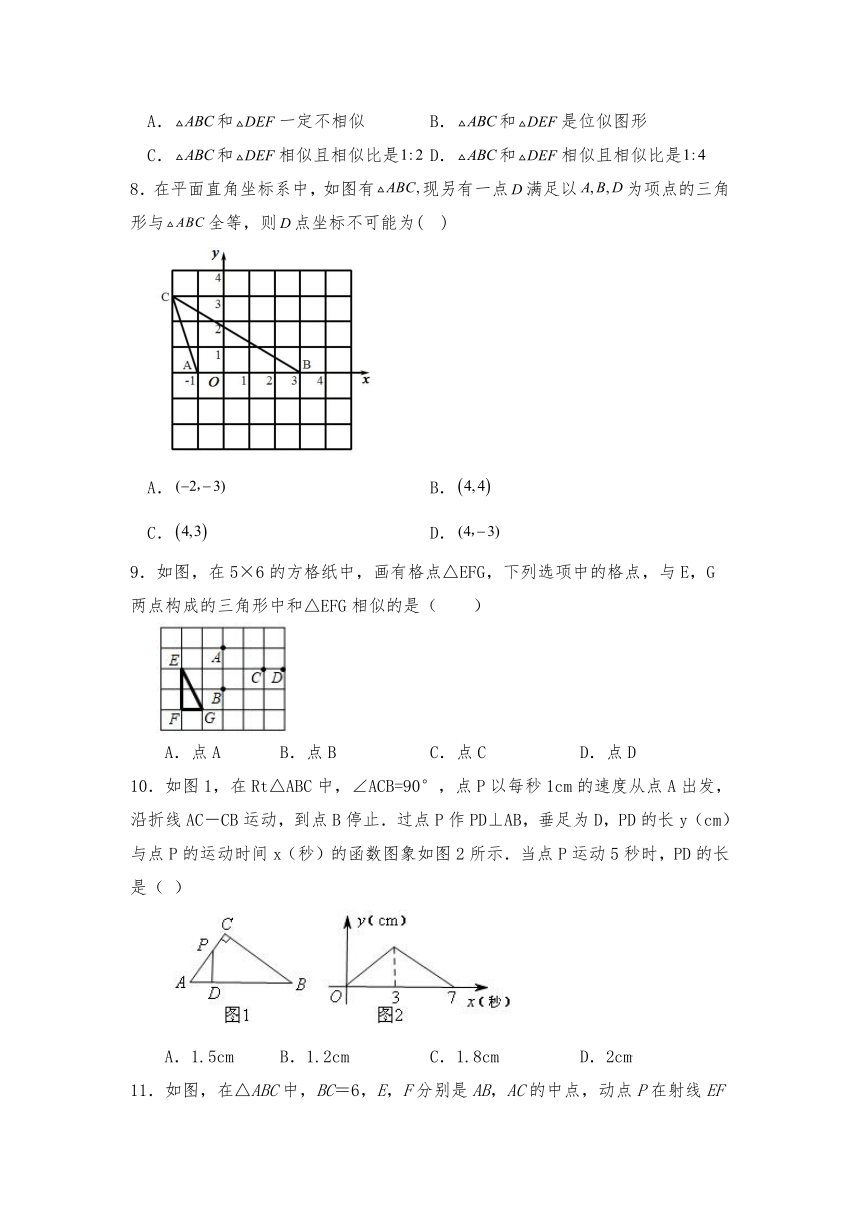
8.在平面直角坐标系中,如图有现另有一点满足以为项点的三角形与全等,则点坐标不可能为( )
A. B.
C. D.
9.如图,在5×6的方格纸中,画有格点△EFG,下列选项中的格点,与E,G两点构成的三角形中和△EFG相似的是( )
A.点A B.点B C.点C D.点D
10.如图1,在Rt△ABC中,∠ACB=90°,点P以每秒1cm的速度从点A出发,沿折线AC-CB运动,到点B停止.过点P作PD⊥AB,垂足为D,PD的长y(cm)与点P的运动时间x(秒)的函数图象如图2所示.当点P运动5秒时,PD的长是( )
A.1.5cm B.1.2cm C.1.8cm D.2cm
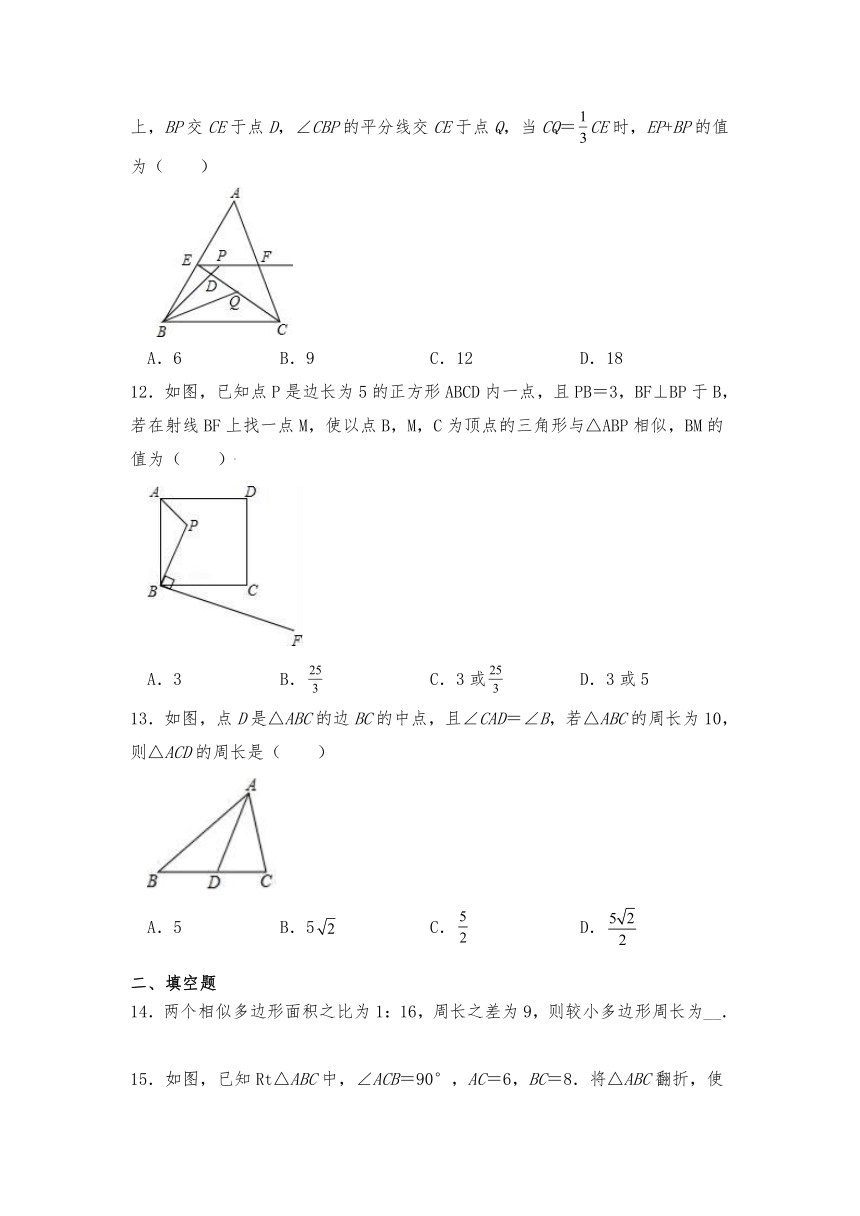
11.如图,在△ABC中,BC=6,E,F分别是AB,AC的中点,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于点Q,当CQ=CE时,EP+BP的值为( )
A.6 B.9 C.12 D.18
12.如图,已知点P是边长为5的正方形ABCD内一点,且PB=3,BF⊥BP于B,若在射线BF上找一点M,使以点B,M,C为顶点的三角形与△ABP相似,BM的值为( )
A.3 B. C.3或 D.3或5
13.如图,点D是△ABC的边BC的中点,且∠CAD=∠B,若△ABC的周长为10,则△ACD的周长是( )
A.5 B.5 C. D.
二、填空题
14.两个相似多边形面积之比为1:16,周长之差为9,则较小多边形周长为__.
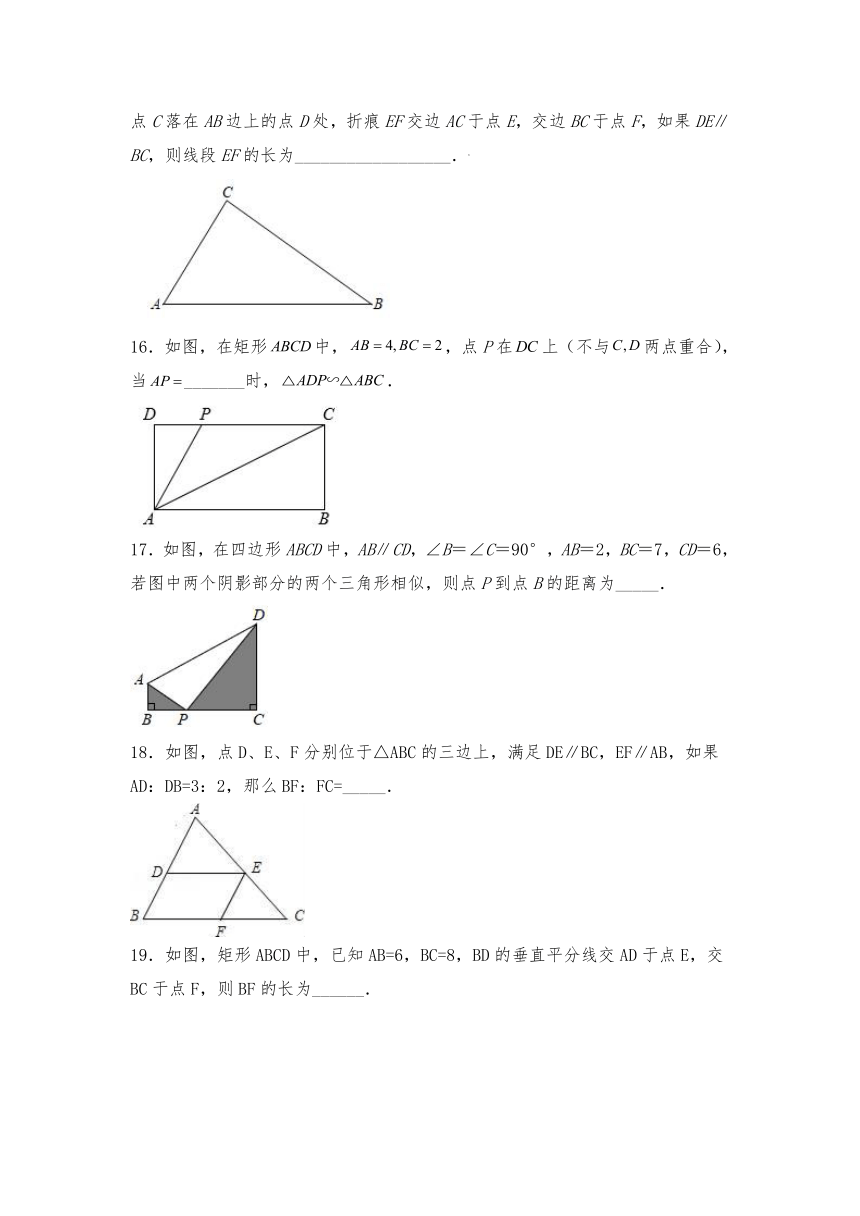
15.如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=8.将△ABC翻折,使点C落在AB边上的点D处,折痕EF交边AC于点E,交边BC于点F,如果DE∥BC,则线段EF的长为__________________.
16.如图,在矩形中,,点P在上(不与两点重合),当_______时,.
17.如图,在四边形ABCD中,AB∥CD,∠B=∠C=90°,AB=2,BC=7,CD=6,若图中两个阴影部分的两个三角形相似,则点P到点B的距离为_____.
18.如图,点D、E、F分别位于△ABC的三边上,满足DE∥BC,EF∥AB,如果AD:DB=3:2,那么BF:FC=_____.
19.如图,矩形ABCD中,已知AB=6,BC=8,BD的垂直平分线交AD于点E,交BC于点F,则BF的长为______.
20.如图,,,,,则________.
21.在方格纸中,每个小格的顶点叫做格点,以格点连线为边的三角形叫做格点三角形.如图,请在边长为1个单位的2×3的方格纸中,找出一个格点三角形DEF.如果△DEF与△ABC相似(相似比不为1),那么△DEF的面积为______.
22.如图,在已建立直角坐标系的4×4的正方形方格纸中,△ABC是格点三角形(三角形的三个顶点都是小正方形的顶点),若以格点P、A、B为顶点的三角形与△ABC相似(C点除外),则格点P的坐标是_____.
三、解答题
23.如图,在梯形中,,若的平分线于点H,,且四边形的面积为21,求的面积.
24.(1)正方形ABCD与等腰直角三角形PAQ如图1所示重叠在一起,其中∠PAQ=90°,点Q在BC上,连接PD,△ADP与△ABQ全等吗?请说明理由.
(2)如图2,O为正方形ABCD对角线的交点,将一直角三角板FPQ的直角顶点F与点O重合转动三角板使两直角边始终与BC、AB相交于点M、N,使探索OM与ON的数量关系,并说明理由.
(3)如图3,将(2)中的“正方形”改成“长方形”,其它的条件不变,且AB=4,AD=6,FM=x,FN=y,试求y与x之间的函数关系式.
25.定义:顶点都在网格点上的四边形叫做格点四边形,端点都在网格点上的线段叫做格点线.如图1,在正方形网格中,格点线DE、CE将格点四边形ABCD分割成三个彼此相似的三角形.请你在图2、图3中分别画出格点线,将阴影四边形分割成三个彼此相似的三角形.
26.如图,在中,,,,点P由点A出发沿方向向终点B以每秒的速度匀速移动,点Q由点B出发沿方向向终点C以每秒的速度匀速移动,速度为.如果动点同时从点A,B出发,当点P或点Q到达终点时运动停止.则当运动几秒时,以点Q,B,P为顶点的三角形与相似?
27.在△ABC中,,BE是AC边上的中线,点D在射线BC上.
(1)如图1,点D在BC边上,,AD与BE相交于点P,过点A作,交BE的延长线于点F,易得的值为 ;
(2)如图2,在△ABC中,,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,,求的值;
(3)在(2)的条件下,若CD=2,AC=6,则BP= .
28.如图,在矩形中,,平分,分别交的延长线于点;连接,过点作,分别交于点.
(1)求的长;(2)求证:.
答案
一、单选题
C.D.C.B.B.A.C.B.D.B.C.C.B.
二、填空题
14.3
15.
16.
17.3或4或.
18. 3:2.
19.
20.
21.1
22.(1,4)或(3,4).
三、解答题
23.解:延长交于点P,∵,平分
∴,
又∵
∴
∴,且,
∵,∴
∴
∵,∴,
∴
设,则
∵,
∴
∴
∴,
∵,
∴
24.(1)△ADP≌△ABQ.
理由:如图1,∵四边形ABCD是正方形,
∴AB=AD,∠B=∠ADP=∠BAD=90°
∵△PAQ是等腰直角三角形,
∴AQ=AP.
∵∠PAQ=90°,
∴∠BAD=∠PAQ,
∴∠BAD-∠QAD=∠PAQ-∠QAD,
∴∠BAQ=∠PAD.
∵在△ADP和△ABQ中,
∴△ADP≌△ABQ(ASA);
(2)OM=ON.
理由:如图2,∵四边形ABCD是正方形,
∴AO=BO,∠AOB=90°,∠OAB=∠OBC=45°.
∴∠AOB=∠POQ,
∴∠AOB-∠NOB=∠POQ-∠NOB,
∴∠AON=∠BOM
∵在△AON和△BOM中,
,
∴△AON≌△BOM(ASA)
∴OM=ON;
(3)如图4,
过点O作OE⊥AB于E,O H⊥BC于H,
∴∠OEN=∠OHM=90°,OE=AD,OH=AB.
∵AB=4,AD=6,
∴OE=3,OH=2.
∵∠ABC=90°,
∴四边形EBHO是矩形,
∴∠EOH=90°,
∴∠EOH=∠POQ,
∴∠EOH-∠EOM=∠POQ-∠EOM,
∴∠EON=∠HOM.
∴△OEN∽△OHM,
∴,
即
∴y=.
25.如图所示:
26.解:设 t(0∵,
∴分两种情况讨论:①当时,,即,解得;
②当时,,即,解得.
综上所述,当运动2.4秒或秒时,以点Q,B,P为顶点的三角形与相似.
27.解:(1)如图1中,
∵AF∥BC,
∴∠F=∠EBC,
∵∠AEF=∠BEC,AE=EC,
∴△AEF≌△CEB(AAS),
∴AF=BC.
设CD=k,则DB=2k,AF=BC=3k,
∵AF∥BC,
∴△APF∽△DPB,
∴,
故答案是:;
(2)如图2,过点A作AF∥DB,交BE的延长线于点F,
设DC=k,由DC:BC=1:2得BC=2k,DB=DC+BC=3k.
∵E是AC中点,
∴AE=CE.
∵AF∥DB,
∴∠F=∠1.
在△AEF和△CEB中,
,
∴△AEF≌△CEB,
∴EF=BE,AF=BC=2k.
∵AF∥DB,
∴△AFP∽△DBP,
∴;
(3)当CD=2时,BC=4,
∵AC=6,
∴EC=AE=3,
∴EB=
∴EF=BE=5,BF=10.
∵,
,
∴BP=BF=×10=6.
故答案为6.
28.(1)解:∵矩形中, ,
∴,
∵平分,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
设,则,
解得
∴;
(2)∵,
∴四边形是平行四边形,
∴,
∴
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
又∵,
∴,
.
一、单选题
1.如图,在中,点D和E分别是边和的中点,连接,与交于点O,若的面积为1,则的面积为( )
A.6 B.9 C.12 D.13.5
2.如图,直角三角板中,,一边平行于的直尺将三角板分成面积相等的三部分.若,则的长为( )
A. B. C. D.
3.如图,在矩形ABCD中,AB=3,BC=4,点E是边BC的中点,连接AE,与对角线BD交于点F.点M是AD边上的一个动点,连接MF、MC,则MF+MC的最小值为( )
A. B.4 C. D.5
4.如图,点,分别在菱形的边,上,且,交于点,延长交的延长线于点.若,则的值为( )
A. B. C. D.
5.如图,ABC中,DE∥BC,AD:BD=1:3,则OE:OB=( )
A.1:3 B.1:4 C.1:5 D.1:6
6.如图,在矩形ABCD中,点H为边BC的中点,点G为线段DH上一点,且∠BGC=90°,延长BG交CD于点E,延长CG交AD于点F,当CD=4,DE=1时,则DF的长为( )
A.2 B. C. D.
7.如图,小正方形的边长均为,关于和的下列说法正确的是( )
A.和一定不相似 B.和是位似图形
C.和相似且相似比是 D.和相似且相似比是
8.在平面直角坐标系中,如图有现另有一点满足以为项点的三角形与全等,则点坐标不可能为( )
A. B.
C. D.
9.如图,在5×6的方格纸中,画有格点△EFG,下列选项中的格点,与E,G两点构成的三角形中和△EFG相似的是( )
A.点A B.点B C.点C D.点D
10.如图1,在Rt△ABC中,∠ACB=90°,点P以每秒1cm的速度从点A出发,沿折线AC-CB运动,到点B停止.过点P作PD⊥AB,垂足为D,PD的长y(cm)与点P的运动时间x(秒)的函数图象如图2所示.当点P运动5秒时,PD的长是( )
A.1.5cm B.1.2cm C.1.8cm D.2cm
11.如图,在△ABC中,BC=6,E,F分别是AB,AC的中点,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于点Q,当CQ=CE时,EP+BP的值为( )
A.6 B.9 C.12 D.18
12.如图,已知点P是边长为5的正方形ABCD内一点,且PB=3,BF⊥BP于B,若在射线BF上找一点M,使以点B,M,C为顶点的三角形与△ABP相似,BM的值为( )
A.3 B. C.3或 D.3或5
13.如图,点D是△ABC的边BC的中点,且∠CAD=∠B,若△ABC的周长为10,则△ACD的周长是( )
A.5 B.5 C. D.
二、填空题
14.两个相似多边形面积之比为1:16,周长之差为9,则较小多边形周长为__.
15.如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=8.将△ABC翻折,使点C落在AB边上的点D处,折痕EF交边AC于点E,交边BC于点F,如果DE∥BC,则线段EF的长为__________________.
16.如图,在矩形中,,点P在上(不与两点重合),当_______时,.
17.如图,在四边形ABCD中,AB∥CD,∠B=∠C=90°,AB=2,BC=7,CD=6,若图中两个阴影部分的两个三角形相似,则点P到点B的距离为_____.
18.如图,点D、E、F分别位于△ABC的三边上,满足DE∥BC,EF∥AB,如果AD:DB=3:2,那么BF:FC=_____.
19.如图,矩形ABCD中,已知AB=6,BC=8,BD的垂直平分线交AD于点E,交BC于点F,则BF的长为______.
20.如图,,,,,则________.
21.在方格纸中,每个小格的顶点叫做格点,以格点连线为边的三角形叫做格点三角形.如图,请在边长为1个单位的2×3的方格纸中,找出一个格点三角形DEF.如果△DEF与△ABC相似(相似比不为1),那么△DEF的面积为______.
22.如图,在已建立直角坐标系的4×4的正方形方格纸中,△ABC是格点三角形(三角形的三个顶点都是小正方形的顶点),若以格点P、A、B为顶点的三角形与△ABC相似(C点除外),则格点P的坐标是_____.
三、解答题
23.如图,在梯形中,,若的平分线于点H,,且四边形的面积为21,求的面积.
24.(1)正方形ABCD与等腰直角三角形PAQ如图1所示重叠在一起,其中∠PAQ=90°,点Q在BC上,连接PD,△ADP与△ABQ全等吗?请说明理由.
(2)如图2,O为正方形ABCD对角线的交点,将一直角三角板FPQ的直角顶点F与点O重合转动三角板使两直角边始终与BC、AB相交于点M、N,使探索OM与ON的数量关系,并说明理由.
(3)如图3,将(2)中的“正方形”改成“长方形”,其它的条件不变,且AB=4,AD=6,FM=x,FN=y,试求y与x之间的函数关系式.
25.定义:顶点都在网格点上的四边形叫做格点四边形,端点都在网格点上的线段叫做格点线.如图1,在正方形网格中,格点线DE、CE将格点四边形ABCD分割成三个彼此相似的三角形.请你在图2、图3中分别画出格点线,将阴影四边形分割成三个彼此相似的三角形.
26.如图,在中,,,,点P由点A出发沿方向向终点B以每秒的速度匀速移动,点Q由点B出发沿方向向终点C以每秒的速度匀速移动,速度为.如果动点同时从点A,B出发,当点P或点Q到达终点时运动停止.则当运动几秒时,以点Q,B,P为顶点的三角形与相似?
27.在△ABC中,,BE是AC边上的中线,点D在射线BC上.
(1)如图1,点D在BC边上,,AD与BE相交于点P,过点A作,交BE的延长线于点F,易得的值为 ;
(2)如图2,在△ABC中,,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,,求的值;
(3)在(2)的条件下,若CD=2,AC=6,则BP= .
28.如图,在矩形中,,平分,分别交的延长线于点;连接,过点作,分别交于点.
(1)求的长;(2)求证:.
答案
一、单选题
C.D.C.B.B.A.C.B.D.B.C.C.B.
二、填空题
14.3
15.
16.
17.3或4或.
18. 3:2.
19.
20.
21.1
22.(1,4)或(3,4).
三、解答题
23.解:延长交于点P,∵,平分
∴,
又∵
∴
∴,且,
∵,∴
∴
∵,∴,
∴
设,则
∵,
∴
∴
∴,
∵,
∴
24.(1)△ADP≌△ABQ.
理由:如图1,∵四边形ABCD是正方形,
∴AB=AD,∠B=∠ADP=∠BAD=90°
∵△PAQ是等腰直角三角形,
∴AQ=AP.
∵∠PAQ=90°,
∴∠BAD=∠PAQ,
∴∠BAD-∠QAD=∠PAQ-∠QAD,
∴∠BAQ=∠PAD.
∵在△ADP和△ABQ中,
∴△ADP≌△ABQ(ASA);
(2)OM=ON.
理由:如图2,∵四边形ABCD是正方形,
∴AO=BO,∠AOB=90°,∠OAB=∠OBC=45°.
∴∠AOB=∠POQ,
∴∠AOB-∠NOB=∠POQ-∠NOB,
∴∠AON=∠BOM
∵在△AON和△BOM中,
,
∴△AON≌△BOM(ASA)
∴OM=ON;
(3)如图4,
过点O作OE⊥AB于E,O H⊥BC于H,
∴∠OEN=∠OHM=90°,OE=AD,OH=AB.
∵AB=4,AD=6,
∴OE=3,OH=2.
∵∠ABC=90°,
∴四边形EBHO是矩形,
∴∠EOH=90°,
∴∠EOH=∠POQ,
∴∠EOH-∠EOM=∠POQ-∠EOM,
∴∠EON=∠HOM.
∴△OEN∽△OHM,
∴,
即
∴y=.
25.如图所示:
26.解:设 t(0
∴分两种情况讨论:①当时,,即,解得;
②当时,,即,解得.
综上所述,当运动2.4秒或秒时,以点Q,B,P为顶点的三角形与相似.
27.解:(1)如图1中,
∵AF∥BC,
∴∠F=∠EBC,
∵∠AEF=∠BEC,AE=EC,
∴△AEF≌△CEB(AAS),
∴AF=BC.
设CD=k,则DB=2k,AF=BC=3k,
∵AF∥BC,
∴△APF∽△DPB,
∴,
故答案是:;
(2)如图2,过点A作AF∥DB,交BE的延长线于点F,
设DC=k,由DC:BC=1:2得BC=2k,DB=DC+BC=3k.
∵E是AC中点,
∴AE=CE.
∵AF∥DB,
∴∠F=∠1.
在△AEF和△CEB中,
,
∴△AEF≌△CEB,
∴EF=BE,AF=BC=2k.
∵AF∥DB,
∴△AFP∽△DBP,
∴;
(3)当CD=2时,BC=4,
∵AC=6,
∴EC=AE=3,
∴EB=
∴EF=BE=5,BF=10.
∵,
,
∴BP=BF=×10=6.
故答案为6.
28.(1)解:∵矩形中, ,
∴,
∵平分,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
设,则,
解得
∴;
(2)∵,
∴四边形是平行四边形,
∴,
∴
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
又∵,
∴,
.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
