九年级数学上册试题 一课一练4.2 平行线分线段成比例-北师大版(含答案)
文档属性
| 名称 | 九年级数学上册试题 一课一练4.2 平行线分线段成比例-北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 597.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-10 21:15:15 | ||
图片预览



文档简介
4.2 平行线分线段成比例
一、单选题
1.如图,在△ABC中,点D在边BC上,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是( )
A.; B.; C.; D..
2.如图,□ABCD中,点E在CD上,AE交BD于点F,若DE =2CE,则等于( )
A. B. C. D.
3.如图,DE∥FG∥BC,若DB=4FB,则EG与GC的关系是( )
A.EG=4GC B.EG=3GC C.EG=GC D.EG=2GC
4.如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F.已知AB=1,BC=3,DE=2,则EF的长为( )
A.4 B.5 C.6 D.8
5.如图,在中,D在AC边上,,O是BD的中点,连接AO并延长交BC于E,则( )
A.1:2 B.1:3 C.1:4 D.2:3
6.如图,在四边形ABCD中,∠A=∠C=90°,DF∥BC,∠ABC的平分线BE交DF于点G,GH⊥DF,点E恰好为DH的中点,若AE=3,CD=2,则GH=( )
A.1 B.2 C.3 D.4
7.△ABC与△DBC如图放置,已知,∠ABC=∠BDC=90°,∠A=60°,BD=CD=2,将△ABC沿BC方向平移至△A'B'C'位置,使得A'C边恰好经过点D,则平移的距离是( )
A.1 B.2﹣2 C.2﹣2 D.2﹣4
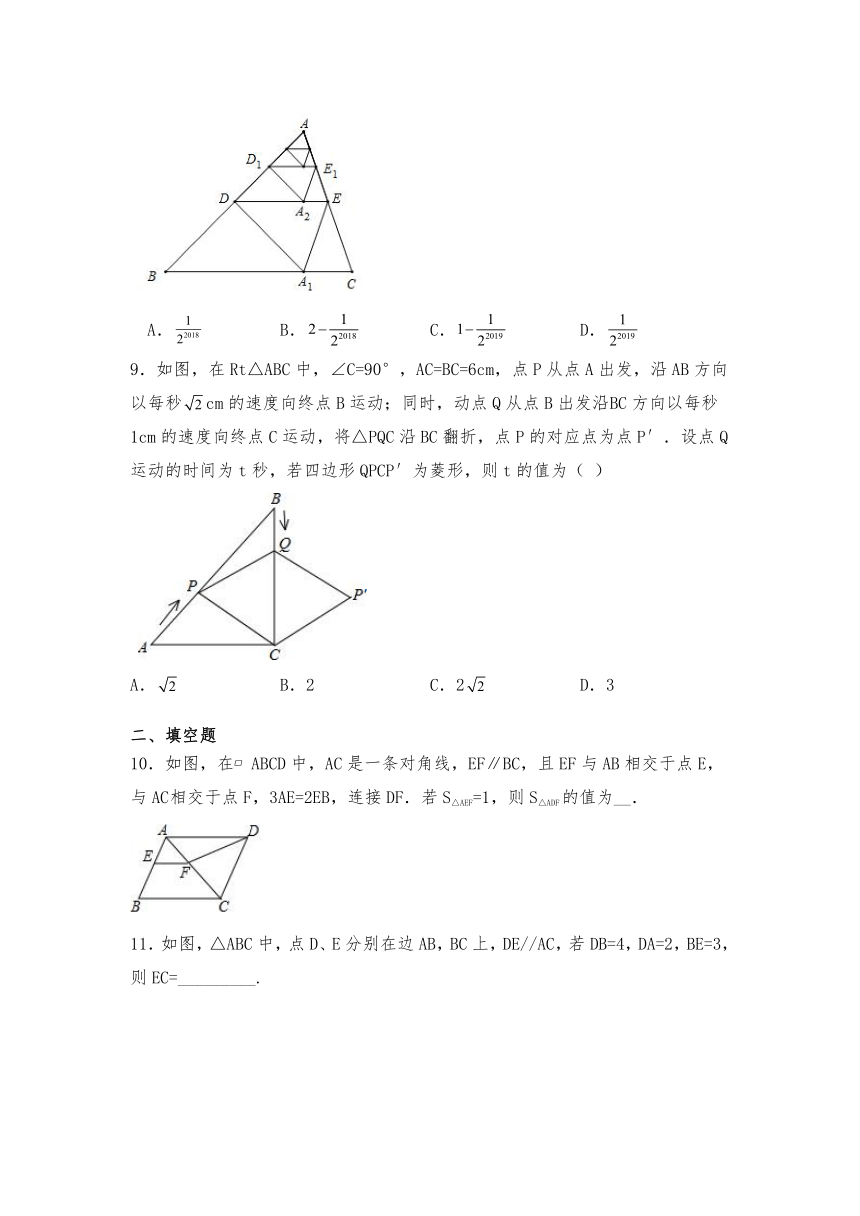
8.如图,将沿着过中点的直线折叠,使点落在边上的,称为第次操作,折痕到的距离记为;还原纸片后,再将沿着过中点的直线折叠,使点落在边上的处,称为第次操作,折痕到的距离记为;按上述方法不断操作下去…,经过第次操作后得到的折痕,到的距离记为,若,则的值为( )
A. B. C. D.
9.如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( )
A. B.2 C.2 D.3
二、填空题
10.如图,在 ABCD中,AC是一条对角线,EF∥BC,且EF与AB相交于点E,与AC相交于点F,3AE=2EB,连接DF.若S△AEF=1,则S△ADF的值为__.
11.如图,△ABC中,点D、E分别在边AB,BC上,DE//AC,若DB=4,DA=2,BE=3,则EC=_________.
12.如图,在中,D,E为边的三等分点,,H为与的交点.若,则___________.
13.把两个含角的直角三角板按如图所示拼接在一起,点为的中点,连结交于点.则=_________.
14.如图,四边形ABCD和四边形ACED都是平行四边形,点R为DE的中点,BR分别交AC、CD于点P、Q.则CP:AC=_____.
15.如图,正方形ABCD中,E,F分别在边AD,CD上,AF,BE相交于点G,若AE=3ED,DF=CF,则AG:GF的值是_______.
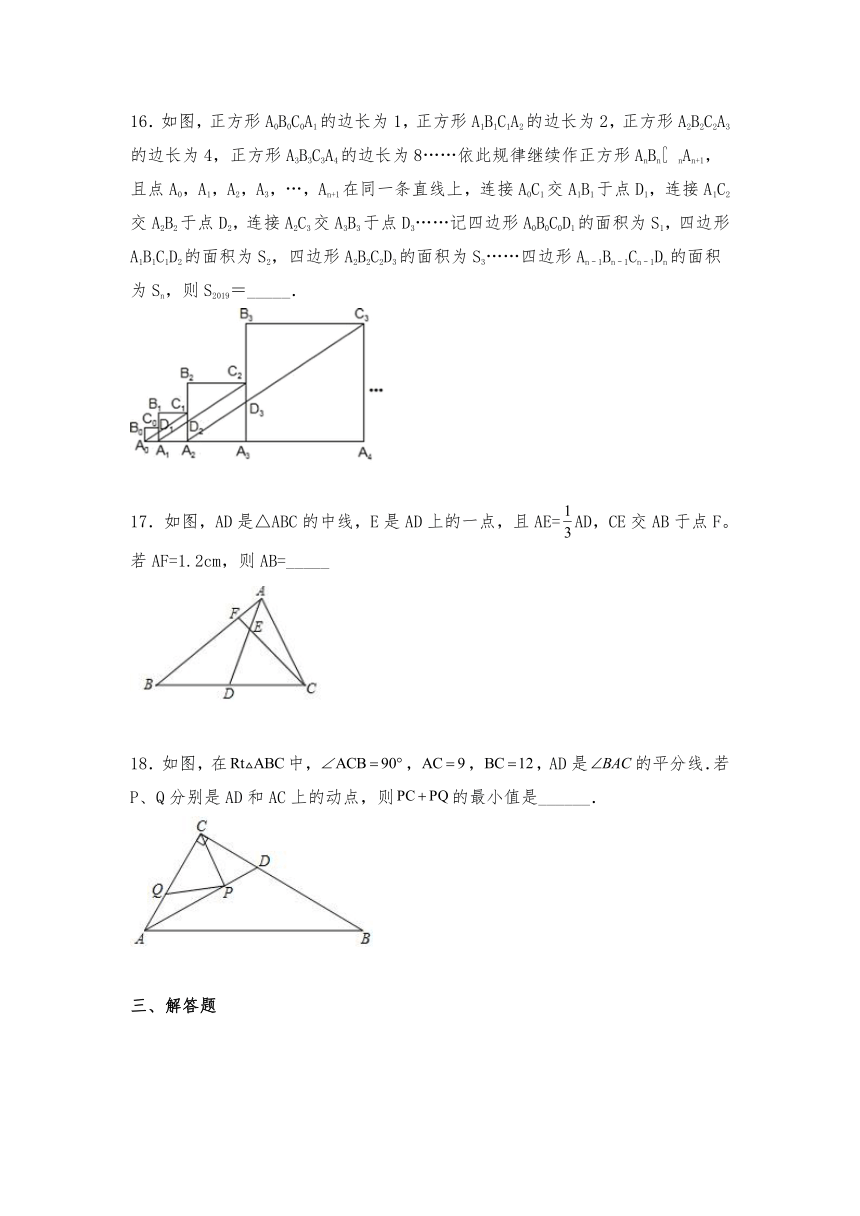
16.如图,正方形A0B0C0A1的边长为1,正方形A1B1C1A2的边长为2,正方形A2B2C2A3的边长为4,正方形A3B3C3A4的边长为8……依此规律继续作正方形AnBn nAn+1,且点A0,A1,A2,A3,…,An+1在同一条直线上,连接A0C1交A1B1于点D1,连接A1C2交A2B2于点D2,连接A2C3交A3B3于点D3……记四边形A0B0C0D1的面积为S1,四边形A1B1C1D2的面积为S2,四边形A2B2C2D3的面积为S3……四边形An﹣1Bn﹣1Cn﹣1Dn的面积为Sn,则S2019=_____.
17.如图,AD是△ABC的中线,E是AD上的一点,且AE=AD,CE交AB于点F。若AF=1.2cm,则AB=_____
18.如图,在中,,,,AD是的平分线.若P、Q分别是AD和AC上的动点,则的最小值是______.
三、解答题
19.已知:平行四边形,是延长线上一点,与、交于、.求证:.
20.如图,在△ABC中,直线DN平行于BC的中线AF,交AB于点D,交AC的延长线于点E,交边BC于点N,
求证:=.
21.如图,在中,点是边上的一点.
(1)请用尺规作图法,在内,求作,使,交于;(不要求写作法,保留作图痕迹)
(2)在(1)的条件下,若,求的值.
22.如图,正方形的边在正方形的边上,连接,过点作,交于点.连接,,其中交于点.
求证:为等腰直角三角形.
若,,求的长.
23.如图,已知AD∥BE∥CF,它们以此交直线l1、l2于点A、B、C和D、E、F.若,AC=14,
(1)求AB的长.
(2)如果AD=7,CF=14,求BE的长.
24.如图,在△ABC中,D为BC边的中点,E为AC边上的任意一点,BE交AD于点O.
某学生在研究这一问题时,发现了如下的事实:
(1)当时,有,如图(1)
(2)当时,有,如图(2)
(3)当时,有,如图(3)
在图(4)中,当时,参照上述研究结论,请你猜想用n表示的一般结论,并给出证明(其中n是正整数)
25.菱形ABCD中,两条对角线AC,BD相交于点O,∠MON+∠BCD=180°,∠MON绕点O旋转,射线OM交边BC于点E,射线ON交边DC于点F,连接EF.
(1)如图1,当∠ABC=90°时,△OEF的形状是 ;
(2)如图2,当∠ABC=60°时,请判断△OEF的形状,并说明理由;
(3)在(1)的条件下,将∠MON的顶点移到AO的中点O′处,∠MO′N绕点O′旋转,仍满足∠MO′N+∠BCD=180°,射线O′M交直线BC于点E,射线O′N交直线CD于点F,当BC=4,且时,直接写出线段CE的长.
26.如图,已知:正方形ABCD,点E在CB的延长线上,连接AE、DE,DE与边AB交于点F,FG∥BE交AE于点G.
(1)求证:GF=BF;
(2)若EB=1,BC=4,求AG的长;
(3)在BC边上取点M,使得BM=BE,连接AM交DE于点O.求证:FO ED=OD EF.
答案
一、单选题
A.D.B.C.B.B.C.B.B.
二、填空题
10.
11..
12.1
13.
14.1:4
15.6:5
16.×42018
17.6cm
18.
三、解答题
19.解:∵四边形是平行四边形,
∴,.
∴,
∴,
即.
20.证明:∵直线DN∥AF,
∴=,=,
∵在△ABC中,AF是BC边上的中线,
∴FB=FC,
∴=.
21.(1)如图所示;
(2)∵,
∴.
∴.
22.(1)∵四边形,四边形都是正方形
∴,,,,
∵,,
∴四边形是平行四边形,
∴,,
∵,,,
∴,
∴,,
∴,
∵,
∴,
∴,且,
∴,且,
∴为等腰直角三角形;
(2)∵,,
∴,,,
∵,
∴,且,
∴,
23.(1)∵AD∥BE∥CF,
∴,
∴,
∵AC=14,
∴AB=4,
(2)过点A作AG∥DF交BE于点H,交CF于点G,如图所示:
又∵AD∥BE∥CF,AD=7,
∴AD=HE=GF=7,
∵CF=14,
∴CG=14﹣7=7,
∵BE∥CF,
∴,
∴BH=2,
∴BE=2+7=9.
24.过D作DF∥BE交AC于F,
∴AO:AD=AE:AF.
∵D为BC边的中点,
∴CF=EF=0.5EC.
∵=,
∴AE:(AE+2EF)=1:(1+n),
AE+2EF=AE+AEn
AEn=2EF,
∴AE:EF=2:n.
∴AE:AF=2:(n+2).
∴=.
25.(1)△OEF是等腰直角三角形;如图1,∵菱形ABCD中,∠ABC=90°,∴四边形ABCD是正方形,∴OB=OC,∠BOC=90°,∠BCD=90°,∠EBO=∠FCO=45°,∴∠BOE+∠COE=90°,∵∠MON+∠BCD=180°,∴∠MON=90°,∴∠COF+∠COE=90°,∴∠BOE=∠COF,在△BOE与△COF中,∵∠BOE=∠COF,OB=OC,∠EBO=∠FCO,∴△BOE≌△COF(ASA),∴OE=OF,∴△OEF是等腰直角三角形;
(2)△OEF是等边三角形;如图2,过O点作OG⊥BC于G,作OH⊥CD于H,∴∠OGE=∠OGC=∠OHC=90°,∵四边形ABCD是菱形,∴CA平分∠BCD,∠ABC+BCD=180°,∴OG=OH,∠BCD=180°﹣60°=120°,∵∠GOH+∠OGC+∠BCD+∠OHC=360°,∴∠GOH+∠BCD=180°,∴∠MON+∠BCD=180°,∴∠GOH=∠EOF=60°,∵∠GOH=∠GOF+∠FOH,∠EOF=∠GOF+∠EOG,∴∠EOG=∠FOH,在△EOG与△FOH中,∵∠EOG=∠FOH,OG=OH,∠EGO=∠FHO,∴△EOG≌△FOH(ASA),∴OE=OF,∴△OEF是等边三角形;
(3)如图3,∵菱形ABCD中,∠ABC=90°,∴四边形ABCD是正方形,∴,过O点作O′G⊥BC于G,作O′H⊥CD于H,∴∠O′GC=∠O′HC=∠BCD=90°,∴四边形O′GCH是矩形,∴O′G∥AB,O′H∥AD,∴,∵AB=BC=CD=AD=4,∴O′G=O′H=3,∴四边形O′GCH是正方形,∴GC=O′G=3,∠GO′H=90°,∵∠MO′N+∠BCD=180°,∴∠EO′F=90°,∴∠EO′F=∠GO′H=90°,∵∠GO′H=∠GO′F+∠FO′H,∠EO′F=∠GO′F+∠EO′G,∴∠EO′G=∠FO′H,在△EO′G与△FO′H中,∵∠EO′G=∠FO′H,O′G= O′H,∠EG O′=∠FH O′,∴△EO′G≌△FO′H(ASA),∴O′E=O′F,∴△O′EF是等腰直角三角形;∵S正方形ABCD=4×4=16,,∴S△O′EF=18,∵S△O′EF=,∴O′E=6,在RT△O′EG中,EG===,∴CE=CG+EG=.根据对称性可知,当∠M′ON′旋转到如图所示位置时,CE′=E′G﹣CG=.
综上可得,线段CE的长为或.
26.解:(1)∵四边形ABCD是正方形,
∴AD∥BC,AB∥CD,AD=CD,
∵GF∥BE,
∴GF∥BC,
∴GF∥AD,
∴,
∵AB∥CD,
,
∵AD=CD,
∴GF=BF;
(2)∵EB=1,BC=4,
∴=4,AE=,
∴=4,
∴AG=;
(3)延长GF交AM于H,
∵GF∥BC,
∴FH∥BC,
∴,
∴,
∵BM=BE,
∴GF=FH,
∵GF∥AD,
∴,,
∴,
∴,
∴FO ED=OD EF.
一、单选题
1.如图,在△ABC中,点D在边BC上,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是( )
A.; B.; C.; D..
2.如图,□ABCD中,点E在CD上,AE交BD于点F,若DE =2CE,则等于( )
A. B. C. D.
3.如图,DE∥FG∥BC,若DB=4FB,则EG与GC的关系是( )
A.EG=4GC B.EG=3GC C.EG=GC D.EG=2GC
4.如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F.已知AB=1,BC=3,DE=2,则EF的长为( )
A.4 B.5 C.6 D.8
5.如图,在中,D在AC边上,,O是BD的中点,连接AO并延长交BC于E,则( )
A.1:2 B.1:3 C.1:4 D.2:3
6.如图,在四边形ABCD中,∠A=∠C=90°,DF∥BC,∠ABC的平分线BE交DF于点G,GH⊥DF,点E恰好为DH的中点,若AE=3,CD=2,则GH=( )
A.1 B.2 C.3 D.4
7.△ABC与△DBC如图放置,已知,∠ABC=∠BDC=90°,∠A=60°,BD=CD=2,将△ABC沿BC方向平移至△A'B'C'位置,使得A'C边恰好经过点D,则平移的距离是( )
A.1 B.2﹣2 C.2﹣2 D.2﹣4
8.如图,将沿着过中点的直线折叠,使点落在边上的,称为第次操作,折痕到的距离记为;还原纸片后,再将沿着过中点的直线折叠,使点落在边上的处,称为第次操作,折痕到的距离记为;按上述方法不断操作下去…,经过第次操作后得到的折痕,到的距离记为,若,则的值为( )
A. B. C. D.
9.如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( )
A. B.2 C.2 D.3
二、填空题
10.如图,在 ABCD中,AC是一条对角线,EF∥BC,且EF与AB相交于点E,与AC相交于点F,3AE=2EB,连接DF.若S△AEF=1,则S△ADF的值为__.
11.如图,△ABC中,点D、E分别在边AB,BC上,DE//AC,若DB=4,DA=2,BE=3,则EC=_________.
12.如图,在中,D,E为边的三等分点,,H为与的交点.若,则___________.
13.把两个含角的直角三角板按如图所示拼接在一起,点为的中点,连结交于点.则=_________.
14.如图,四边形ABCD和四边形ACED都是平行四边形,点R为DE的中点,BR分别交AC、CD于点P、Q.则CP:AC=_____.
15.如图,正方形ABCD中,E,F分别在边AD,CD上,AF,BE相交于点G,若AE=3ED,DF=CF,则AG:GF的值是_______.
16.如图,正方形A0B0C0A1的边长为1,正方形A1B1C1A2的边长为2,正方形A2B2C2A3的边长为4,正方形A3B3C3A4的边长为8……依此规律继续作正方形AnBn nAn+1,且点A0,A1,A2,A3,…,An+1在同一条直线上,连接A0C1交A1B1于点D1,连接A1C2交A2B2于点D2,连接A2C3交A3B3于点D3……记四边形A0B0C0D1的面积为S1,四边形A1B1C1D2的面积为S2,四边形A2B2C2D3的面积为S3……四边形An﹣1Bn﹣1Cn﹣1Dn的面积为Sn,则S2019=_____.
17.如图,AD是△ABC的中线,E是AD上的一点,且AE=AD,CE交AB于点F。若AF=1.2cm,则AB=_____
18.如图,在中,,,,AD是的平分线.若P、Q分别是AD和AC上的动点,则的最小值是______.
三、解答题
19.已知:平行四边形,是延长线上一点,与、交于、.求证:.
20.如图,在△ABC中,直线DN平行于BC的中线AF,交AB于点D,交AC的延长线于点E,交边BC于点N,
求证:=.
21.如图,在中,点是边上的一点.
(1)请用尺规作图法,在内,求作,使,交于;(不要求写作法,保留作图痕迹)
(2)在(1)的条件下,若,求的值.
22.如图,正方形的边在正方形的边上,连接,过点作,交于点.连接,,其中交于点.
求证:为等腰直角三角形.
若,,求的长.
23.如图,已知AD∥BE∥CF,它们以此交直线l1、l2于点A、B、C和D、E、F.若,AC=14,
(1)求AB的长.
(2)如果AD=7,CF=14,求BE的长.
24.如图,在△ABC中,D为BC边的中点,E为AC边上的任意一点,BE交AD于点O.
某学生在研究这一问题时,发现了如下的事实:
(1)当时,有,如图(1)
(2)当时,有,如图(2)
(3)当时,有,如图(3)
在图(4)中,当时,参照上述研究结论,请你猜想用n表示的一般结论,并给出证明(其中n是正整数)
25.菱形ABCD中,两条对角线AC,BD相交于点O,∠MON+∠BCD=180°,∠MON绕点O旋转,射线OM交边BC于点E,射线ON交边DC于点F,连接EF.
(1)如图1,当∠ABC=90°时,△OEF的形状是 ;
(2)如图2,当∠ABC=60°时,请判断△OEF的形状,并说明理由;
(3)在(1)的条件下,将∠MON的顶点移到AO的中点O′处,∠MO′N绕点O′旋转,仍满足∠MO′N+∠BCD=180°,射线O′M交直线BC于点E,射线O′N交直线CD于点F,当BC=4,且时,直接写出线段CE的长.
26.如图,已知:正方形ABCD,点E在CB的延长线上,连接AE、DE,DE与边AB交于点F,FG∥BE交AE于点G.
(1)求证:GF=BF;
(2)若EB=1,BC=4,求AG的长;
(3)在BC边上取点M,使得BM=BE,连接AM交DE于点O.求证:FO ED=OD EF.
答案
一、单选题
A.D.B.C.B.B.C.B.B.
二、填空题
10.
11..
12.1
13.
14.1:4
15.6:5
16.×42018
17.6cm
18.
三、解答题
19.解:∵四边形是平行四边形,
∴,.
∴,
∴,
即.
20.证明:∵直线DN∥AF,
∴=,=,
∵在△ABC中,AF是BC边上的中线,
∴FB=FC,
∴=.
21.(1)如图所示;
(2)∵,
∴.
∴.
22.(1)∵四边形,四边形都是正方形
∴,,,,
∵,,
∴四边形是平行四边形,
∴,,
∵,,,
∴,
∴,,
∴,
∵,
∴,
∴,且,
∴,且,
∴为等腰直角三角形;
(2)∵,,
∴,,,
∵,
∴,且,
∴,
23.(1)∵AD∥BE∥CF,
∴,
∴,
∵AC=14,
∴AB=4,
(2)过点A作AG∥DF交BE于点H,交CF于点G,如图所示:
又∵AD∥BE∥CF,AD=7,
∴AD=HE=GF=7,
∵CF=14,
∴CG=14﹣7=7,
∵BE∥CF,
∴,
∴BH=2,
∴BE=2+7=9.
24.过D作DF∥BE交AC于F,
∴AO:AD=AE:AF.
∵D为BC边的中点,
∴CF=EF=0.5EC.
∵=,
∴AE:(AE+2EF)=1:(1+n),
AE+2EF=AE+AEn
AEn=2EF,
∴AE:EF=2:n.
∴AE:AF=2:(n+2).
∴=.
25.(1)△OEF是等腰直角三角形;如图1,∵菱形ABCD中,∠ABC=90°,∴四边形ABCD是正方形,∴OB=OC,∠BOC=90°,∠BCD=90°,∠EBO=∠FCO=45°,∴∠BOE+∠COE=90°,∵∠MON+∠BCD=180°,∴∠MON=90°,∴∠COF+∠COE=90°,∴∠BOE=∠COF,在△BOE与△COF中,∵∠BOE=∠COF,OB=OC,∠EBO=∠FCO,∴△BOE≌△COF(ASA),∴OE=OF,∴△OEF是等腰直角三角形;
(2)△OEF是等边三角形;如图2,过O点作OG⊥BC于G,作OH⊥CD于H,∴∠OGE=∠OGC=∠OHC=90°,∵四边形ABCD是菱形,∴CA平分∠BCD,∠ABC+BCD=180°,∴OG=OH,∠BCD=180°﹣60°=120°,∵∠GOH+∠OGC+∠BCD+∠OHC=360°,∴∠GOH+∠BCD=180°,∴∠MON+∠BCD=180°,∴∠GOH=∠EOF=60°,∵∠GOH=∠GOF+∠FOH,∠EOF=∠GOF+∠EOG,∴∠EOG=∠FOH,在△EOG与△FOH中,∵∠EOG=∠FOH,OG=OH,∠EGO=∠FHO,∴△EOG≌△FOH(ASA),∴OE=OF,∴△OEF是等边三角形;
(3)如图3,∵菱形ABCD中,∠ABC=90°,∴四边形ABCD是正方形,∴,过O点作O′G⊥BC于G,作O′H⊥CD于H,∴∠O′GC=∠O′HC=∠BCD=90°,∴四边形O′GCH是矩形,∴O′G∥AB,O′H∥AD,∴,∵AB=BC=CD=AD=4,∴O′G=O′H=3,∴四边形O′GCH是正方形,∴GC=O′G=3,∠GO′H=90°,∵∠MO′N+∠BCD=180°,∴∠EO′F=90°,∴∠EO′F=∠GO′H=90°,∵∠GO′H=∠GO′F+∠FO′H,∠EO′F=∠GO′F+∠EO′G,∴∠EO′G=∠FO′H,在△EO′G与△FO′H中,∵∠EO′G=∠FO′H,O′G= O′H,∠EG O′=∠FH O′,∴△EO′G≌△FO′H(ASA),∴O′E=O′F,∴△O′EF是等腰直角三角形;∵S正方形ABCD=4×4=16,,∴S△O′EF=18,∵S△O′EF=,∴O′E=6,在RT△O′EG中,EG===,∴CE=CG+EG=.根据对称性可知,当∠M′ON′旋转到如图所示位置时,CE′=E′G﹣CG=.
综上可得,线段CE的长为或.
26.解:(1)∵四边形ABCD是正方形,
∴AD∥BC,AB∥CD,AD=CD,
∵GF∥BE,
∴GF∥BC,
∴GF∥AD,
∴,
∵AB∥CD,
,
∵AD=CD,
∴GF=BF;
(2)∵EB=1,BC=4,
∴=4,AE=,
∴=4,
∴AG=;
(3)延长GF交AM于H,
∵GF∥BC,
∴FH∥BC,
∴,
∴,
∵BM=BE,
∴GF=FH,
∵GF∥AD,
∴,,
∴,
∴,
∴FO ED=OD EF.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
