九年级数学上册试题 一课一练4.5 相似三角形判定定理的证明-北师大版(含答案)
文档属性
| 名称 | 九年级数学上册试题 一课一练4.5 相似三角形判定定理的证明-北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 379.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-10 21:16:07 | ||
图片预览




文档简介
4.5 相似三角形判定定理的证明
一、单选题
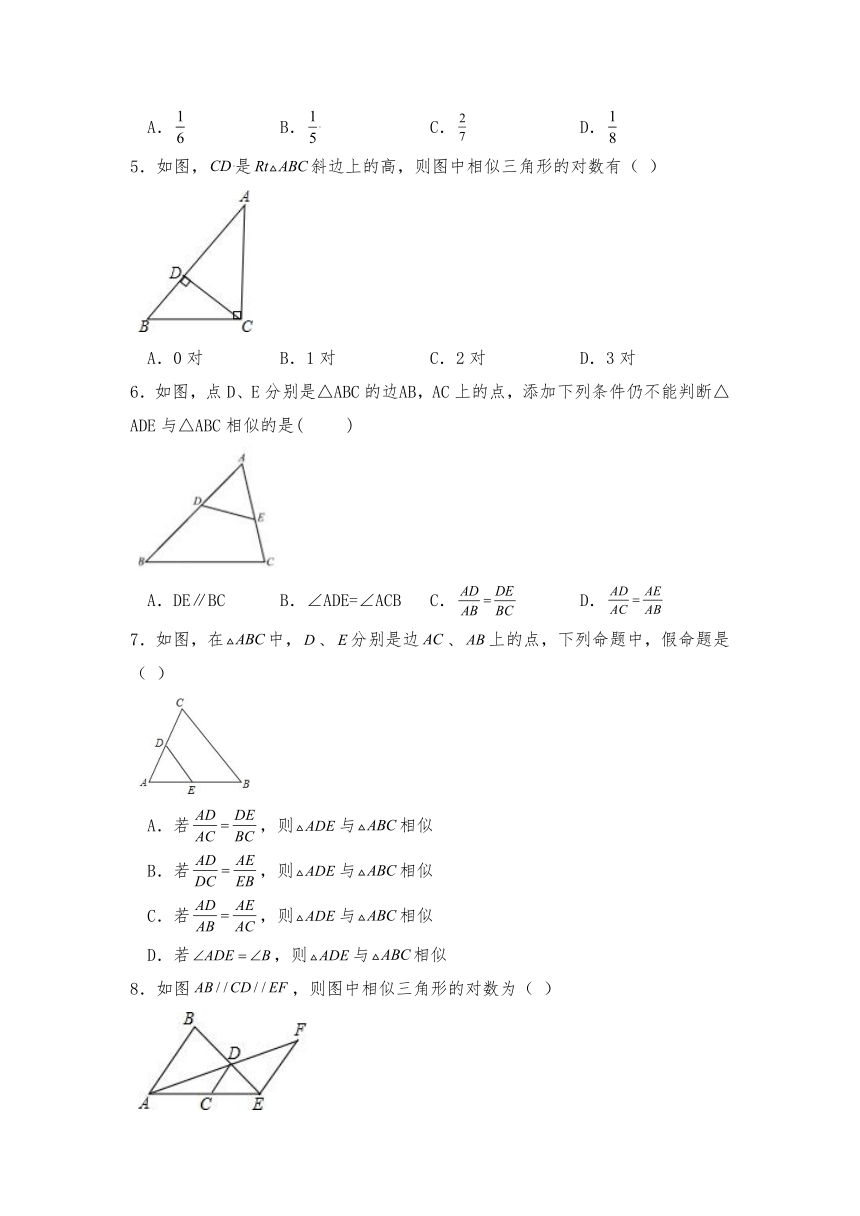
1.如图,在中,点P在边AB上,则在下列四个条件中::;;;,能满足与相似的条件是( )
A. B. C. D.
2.如图,在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判断△ABC∽△AED的是( )
A.∠AED=∠B B.∠ADE=∠C C. D.
3.图中四个阴影的三角形中与△ABC相似的是( )
A. B. C. D.
4.如图,在平行四边形ABCD中,E、F分别是BC边,CD边的中点,AE、AF分别交BD于点G,H,设△AGH的面积为S1,平行四边形ABCD的面积为S2,则S1:S2的值为( )
A. B. C. D.
5.如图,是斜边上的高,则图中相似三角形的对数有( )
A.0对 B.1对 C.2对 D.3对
6.如图,点D、E分别是△ABC的边AB,AC上的点,添加下列条件仍不能判断△ADE与△ABC相似的是( )
A.DE∥BC B.∠ADE=∠ACB C. D.
7.如图,在中,、分别是边、上的点,下列命题中,假命题是( )
若,则与相似
B.若,则与相似
C.若,则与相似
D.若,则与相似
8.如图,则图中相似三角形的对数为( )
A.1对 B.2对 C.3对 D.4对
9.如图,把△ABC沿着BC的方向平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半,若BC=,则△ABC移动的距离是( )
A. B. C. D.﹣
10.如图,在 ABCD中,E为CD的中点,AE交BD于点O,S△DOE=12cm2,则S△AOB等于( )
A.24cm2 B.36cm2 C.48cm2 D.60cm2
11.如图,正方形中,为上一点,,交的延长线于点.若,,则的长为( )
A.18 B. C. D.
二、填空题
12.如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=,则BD的长为_______.
13.如图,∠C=∠E=90°,AC=3,BC=4,AE=2,则AD=______.
14.如图,在中,,,,点是边上的动点(点与点、不重合),过动点作交于点.若与相似,则________.
15.如图,在正方形中,是的中点,是上一点,且,给出下列结论:①;②;③;④.其中正确结论的序号为________.
16.如图,已知,,,,要使,只要________.
17.如图所示,正方形ABCD的边长为2,BE=CE,MN=1,线段MN的两端点在CD、AD上滑动,当MD=____________时,△ABE与以D、M、N为顶点的三角形相似.
18.如图,在中,,,直角的顶点在上,、分别交、于点、,绕点任意旋转.当时,的值为________;当时,为________.(用含的式子表示)
19.如图,与是两个全等的等腰直角三角形,,分别与相交于点.则图中不全等的相似三角形有________对,分别是______________________.
20.如图所示,在四边形中,,如果要使,那么还要补充的一个条件是________.(只要求写出一个条件即可)
21.如图,G是△ABC的重心,直线l过A点与BC平行.若直线CG分别与AB,直线l交于点D,E两点,直线BG与AC交于F点,则△AED的面积∶四边形ADGF的面积=_________________.
22.如图所示,在中,是高,,,,,则________.
三、解答题
23.如图,在△ABC中,AB=AC,点D,E分别在BC,AB上,且∠BDE=∠CAD.求证:△ADE∽△ABD.
24.已知:如图,在△ABC中,点D、E分别在边AB、AC上,且∠ABE =∠ACD,BE、CD交于点G.
(1)求证:△AED∽△ABC;
(2)如果BE平分∠ABC,求证:DE=CE.
25.如图,等边三角形ABC的边长为3,点P为BC边上一点,且BP=1,点D为AC边上一点,若∠APD=60°,
证明:△ACP∽△APD.
26.如图,,,又,点,,在同一条直线上.求证:.
27.已知:如图,∠1=∠2,AB AC=AD AE.求证:∠C=∠E.
28.如图,点M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B,且DM交AC于点F,ME交BC于点G.写出图中的所有相似三角形,并选择一对加以证明.
答案
一、单选题
D.D.B.A.D.C.A.C.D.C.B.
二、填空题
12.2.
13..
14.或
15.①②③
16.
17.或
18.,
19.3
20.或或
21.3:2
22.2.4
三、解答题
23.∵AB=AC,
∴∠B=∠C.
∵∠ADB=∠C+∠CAD=∠BDE+∠ADE,∠BDE=∠CAD,
∴∠ADE=∠C,∠B=∠ADE.
∵∠DAE=∠BAD,
∴△ADE∽△ABD.
24.解:(1)∵∠ABE =∠ACD,且∠A是公共角,
∴△ABE∽△ACD.
∴,即,
又∵∠A是公共角,
∴△AED∽△ABC.
(2)在BC上截取BF=BD,连接EF,
在△BDE与△BFE中,BD=BF,∠DBE=∠FBE,BE=BE,
∴△BDE≌△BFE,
∴DE=FE,∠BDE=∠BFE,∴∠ADE=∠EFC,
∵△AED∽△ABC,∴∠ADE=∠ACB,
∴∠EFC=∠ACB,
∴EF=EC,
∴DE=CE.
25.∵△ABC为等边三角形,
∴∠C=60°,
∵∠PAD=∠CAP,∠APD=∠C=60°,
∴△ACP∽△APD.
26.证明:∵,,
∴,
∵,
∴,
∴.
27.证明:在△ABE和△ADC中,
∵AB AC=AD AE,∴,
又∵∠1=∠2,
∴△ABE∽△ADC,
∴∠C=∠E.
28.图中的相似三角形有:△AMF∽△BGM,△DMG∽△DBM,△EMF∽△EAM.
以下证明△AMF∽△BGM.
∵∠AFM=∠DME+∠E(外角定理),∠DME=∠A=∠B(已知),∴∠AFM=∠DME+∠E=∠A+∠E=∠BMG,∠A=∠B,∴△AMF∽△BGM.
一、单选题
1.如图,在中,点P在边AB上,则在下列四个条件中::;;;,能满足与相似的条件是( )
A. B. C. D.
2.如图,在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判断△ABC∽△AED的是( )
A.∠AED=∠B B.∠ADE=∠C C. D.
3.图中四个阴影的三角形中与△ABC相似的是( )
A. B. C. D.
4.如图,在平行四边形ABCD中,E、F分别是BC边,CD边的中点,AE、AF分别交BD于点G,H,设△AGH的面积为S1,平行四边形ABCD的面积为S2,则S1:S2的值为( )
A. B. C. D.
5.如图,是斜边上的高,则图中相似三角形的对数有( )
A.0对 B.1对 C.2对 D.3对
6.如图,点D、E分别是△ABC的边AB,AC上的点,添加下列条件仍不能判断△ADE与△ABC相似的是( )
A.DE∥BC B.∠ADE=∠ACB C. D.
7.如图,在中,、分别是边、上的点,下列命题中,假命题是( )
若,则与相似
B.若,则与相似
C.若,则与相似
D.若,则与相似
8.如图,则图中相似三角形的对数为( )
A.1对 B.2对 C.3对 D.4对
9.如图,把△ABC沿着BC的方向平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半,若BC=,则△ABC移动的距离是( )
A. B. C. D.﹣
10.如图,在 ABCD中,E为CD的中点,AE交BD于点O,S△DOE=12cm2,则S△AOB等于( )
A.24cm2 B.36cm2 C.48cm2 D.60cm2
11.如图,正方形中,为上一点,,交的延长线于点.若,,则的长为( )
A.18 B. C. D.
二、填空题
12.如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=,则BD的长为_______.
13.如图,∠C=∠E=90°,AC=3,BC=4,AE=2,则AD=______.
14.如图,在中,,,,点是边上的动点(点与点、不重合),过动点作交于点.若与相似,则________.
15.如图,在正方形中,是的中点,是上一点,且,给出下列结论:①;②;③;④.其中正确结论的序号为________.
16.如图,已知,,,,要使,只要________.
17.如图所示,正方形ABCD的边长为2,BE=CE,MN=1,线段MN的两端点在CD、AD上滑动,当MD=____________时,△ABE与以D、M、N为顶点的三角形相似.
18.如图,在中,,,直角的顶点在上,、分别交、于点、,绕点任意旋转.当时,的值为________;当时,为________.(用含的式子表示)
19.如图,与是两个全等的等腰直角三角形,,分别与相交于点.则图中不全等的相似三角形有________对,分别是______________________.
20.如图所示,在四边形中,,如果要使,那么还要补充的一个条件是________.(只要求写出一个条件即可)
21.如图,G是△ABC的重心,直线l过A点与BC平行.若直线CG分别与AB,直线l交于点D,E两点,直线BG与AC交于F点,则△AED的面积∶四边形ADGF的面积=_________________.
22.如图所示,在中,是高,,,,,则________.
三、解答题
23.如图,在△ABC中,AB=AC,点D,E分别在BC,AB上,且∠BDE=∠CAD.求证:△ADE∽△ABD.
24.已知:如图,在△ABC中,点D、E分别在边AB、AC上,且∠ABE =∠ACD,BE、CD交于点G.
(1)求证:△AED∽△ABC;
(2)如果BE平分∠ABC,求证:DE=CE.
25.如图,等边三角形ABC的边长为3,点P为BC边上一点,且BP=1,点D为AC边上一点,若∠APD=60°,
证明:△ACP∽△APD.
26.如图,,,又,点,,在同一条直线上.求证:.
27.已知:如图,∠1=∠2,AB AC=AD AE.求证:∠C=∠E.
28.如图,点M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B,且DM交AC于点F,ME交BC于点G.写出图中的所有相似三角形,并选择一对加以证明.
答案
一、单选题
D.D.B.A.D.C.A.C.D.C.B.
二、填空题
12.2.
13..
14.或
15.①②③
16.
17.或
18.,
19.3
20.或或
21.3:2
22.2.4
三、解答题
23.∵AB=AC,
∴∠B=∠C.
∵∠ADB=∠C+∠CAD=∠BDE+∠ADE,∠BDE=∠CAD,
∴∠ADE=∠C,∠B=∠ADE.
∵∠DAE=∠BAD,
∴△ADE∽△ABD.
24.解:(1)∵∠ABE =∠ACD,且∠A是公共角,
∴△ABE∽△ACD.
∴,即,
又∵∠A是公共角,
∴△AED∽△ABC.
(2)在BC上截取BF=BD,连接EF,
在△BDE与△BFE中,BD=BF,∠DBE=∠FBE,BE=BE,
∴△BDE≌△BFE,
∴DE=FE,∠BDE=∠BFE,∴∠ADE=∠EFC,
∵△AED∽△ABC,∴∠ADE=∠ACB,
∴∠EFC=∠ACB,
∴EF=EC,
∴DE=CE.
25.∵△ABC为等边三角形,
∴∠C=60°,
∵∠PAD=∠CAP,∠APD=∠C=60°,
∴△ACP∽△APD.
26.证明:∵,,
∴,
∵,
∴,
∴.
27.证明:在△ABE和△ADC中,
∵AB AC=AD AE,∴,
又∵∠1=∠2,
∴△ABE∽△ADC,
∴∠C=∠E.
28.图中的相似三角形有:△AMF∽△BGM,△DMG∽△DBM,△EMF∽△EAM.
以下证明△AMF∽△BGM.
∵∠AFM=∠DME+∠E(外角定理),∠DME=∠A=∠B(已知),∴∠AFM=∠DME+∠E=∠A+∠E=∠BMG,∠A=∠B,∴△AMF∽△BGM.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
