等腰三角形
图片预览







文档简介
课件26张PPT。等腰三角形 教学目标: 1.了解等腰三角形的概念。 2.探索并证明等腰三角形的性质定理。
教学重点:探索并证明等腰三角形的性质定理。
教学难点:等腰三角形“三线合一”的性质。
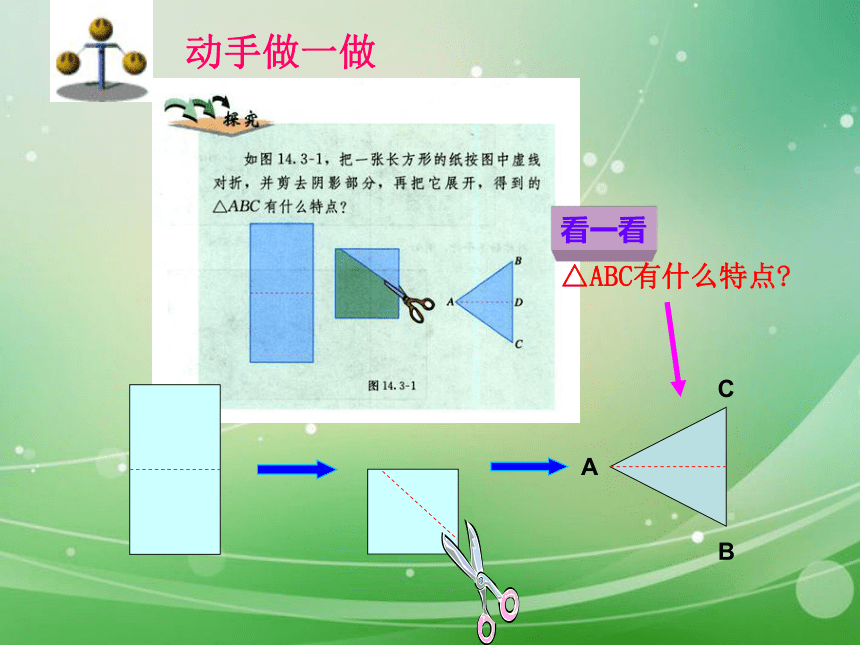
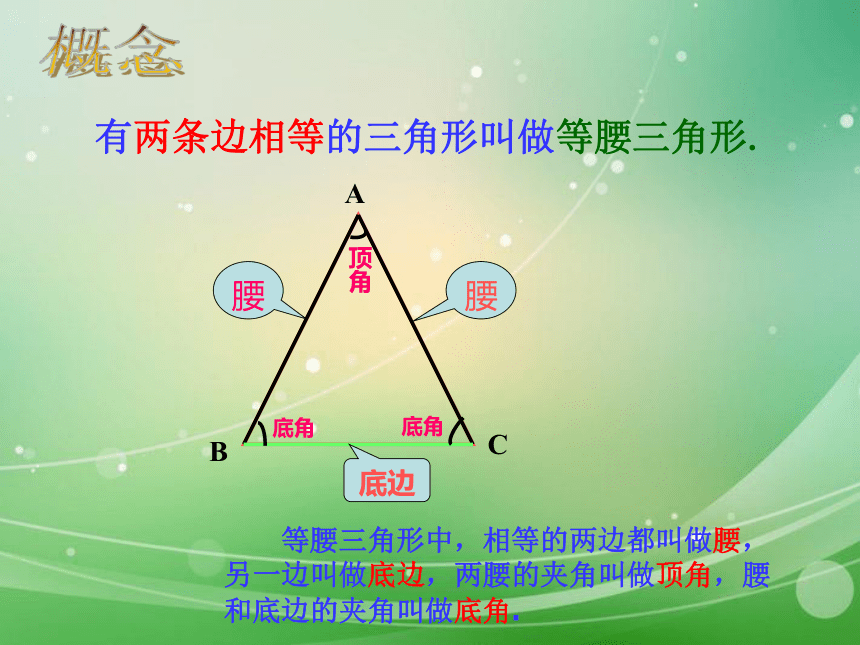
动手做一做△ABC有什么特点?看一看有两条边相等的三角形叫做等腰三角形. 等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.底边概念 1、等腰三角形一腰为3cm,底为4cm,则它的周长
是 ;
2、等腰三角形的一边长为3cm,另一边长为4cm,则它的周长是 ;
3、等腰三角形的一边长为3cm,另一边长为8cm,则它的周长是 。
10 cm10 cm 或 11 cm19 cm小试牛刀 等腰三角形是轴对称图形吗?
思考是※等腰三角形是轴对称图形,对称轴是顶角平分线所在的直线。 AC B D AB=AC BD=CD AD=AD ∠B = ∠C∠BAD = ∠CAD∠ADB = ∠ADC 等腰三角形除了两腰相等以外, 你还能发现它的其他性质吗? 大胆猜想猜想与论证等腰三角形的两个底角相等。已知:△ABC中,AB=AC求证:∠B=?C分析:1.如何证明两个角相等? 2.如何构造两个全等的三角形?猜想则有∠1=∠2D12在△ABD和△ACD中证明: 作顶角的平分线AD,AB=AC ∠1=∠2 AD=AD (公共边) ∴ △ABD≌ △ACD (SAS) ∴ ∠B=∠C (全等三角形对应角相等) 方法一则有 BD=CDD在△ABD和△ACD中证明: 作△ABC 的中线ADAB=AC BD=CDAD=AD (公共边) ∴ △ABD≌ △ACD (SSS) ∴ ∠B=∠C (全等三角形对应角相等) 方法二则有 ∠ADB=∠ADC =90oD在Rt△ABD和Rt△ACD中证明: 作△ABC 的高线ADAB=AC AD=AD (公共边) ∴ Rt△ABD≌Rt△ACD (HL) ∴ ∠B=∠C (全等三角形对应角相等) 方法三猜想与论证等腰三角形的两个底角相等。已知:△ABC中,AB=AC求证:∠B=?C分析:1.如何证明两个角相等? 2.如何构造两个全等的三角形?性质1(等边对等角)猜想⒈等腰三角形一个底角为75°,它的另外两个
角为_____ __;
⒉等腰三角形一个角为70°,它的另外两个角
为___________________;
⒊等腰三角形一个角为110°,它的另外两个角
为______ __。75°, 30°70°,40°或55°,55°35°,35°小试牛刀想一想: 刚才的证明除了能得到∠B=∠C 你还能发现什么?
A B D C AB=AC BD=CD AD=AD ∠B = ∠C.∠BAD = ∠CAD ∠ADB =∠ADC=90°等腰三角形顶角的平分线平分底边并且垂直于底边.性质2(等腰三角形三线合一)练习:选一选:1.(13年钦州)等腰三角形的一个角是80°,则它的顶角度数是( )
A.80° B.80°或20° C.80°或50° D.20°
2.(13年南充)在△ABC中,AB=AC,∠B=70°,则∠A=( )
A.70° B.55° C.50° D.40°
3.已知等腰三角形的一个内角为70°,则另外两个内角的度数是( )
A.55°,55° B.70°,40° C.55°,55°,或70°,40° D.以上都不对
如图:△ABC中,AB=AC。
(1)若AD平分∠BAC,则∠BDA= ,
BD= 。
(2)若BD=CD,则AD平分 ,
∠ADC=
(3)若AD⊥BC,则∠BAD= ,BC=2( )动手做一做ABCD如图,三角形ABC中,AC=BC,CD是∠ACB的平分线,AD=4cm,求AB的长及∠CDB的大小。CABD 轴对称图形两个底角相等,简称“等边对等角”顶角平分线、底边上的中线、和底边上的高
互相重合,简称“三线合 一”等腰三角形小 结性质1 : 等腰三角形的两个底角相等 (简称“等边对等角”,前提是在同一个三角形中。) 性质2 : 等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合。 (简称“三线合一”,前提是在同一个等腰三角形中。)
布置作业 1、预习课本P77-79,《名师大课堂》41页课前预习
2、书面作业:P81第1、3、4、7题,名师点拨本节练习谢谢指导再 见
是 ;
2、等腰三角形的一边长为3cm,另一边长为4cm,则它的周长是 ;
3、等腰三角形的一边长为3cm,另一边长为8cm,则它的周长是 。
10 cm10 cm 或 11 cm19 cm小试牛刀 等腰三角形是轴对称图形吗?
思考是※等腰三角形是轴对称图形,对称轴是顶角平分线所在的直线。 AC B D AB=AC BD=CD AD=AD ∠B = ∠C∠BAD = ∠CAD∠ADB = ∠ADC 等腰三角形除了两腰相等以外, 你还能发现它的其他性质吗? 大胆猜想猜想与论证等腰三角形的两个底角相等。已知:△ABC中,AB=AC求证:∠B=?C分析:1.如何证明两个角相等? 2.如何构造两个全等的三角形?猜想则有∠1=∠2D12在△ABD和△ACD中证明: 作顶角的平分线AD,AB=AC ∠1=∠2 AD=AD (公共边) ∴ △ABD≌ △ACD (SAS) ∴ ∠B=∠C (全等三角形对应角相等) 方法一则有 BD=CDD在△ABD和△ACD中证明: 作△ABC 的中线ADAB=AC BD=CDAD=AD (公共边) ∴ △ABD≌ △ACD (SSS) ∴ ∠B=∠C (全等三角形对应角相等) 方法二则有 ∠ADB=∠ADC =90oD在Rt△ABD和Rt△ACD中证明: 作△ABC 的高线ADAB=AC AD=AD (公共边) ∴ Rt△ABD≌Rt△ACD (HL) ∴ ∠B=∠C (全等三角形对应角相等) 方法三猜想与论证等腰三角形的两个底角相等。已知:△ABC中,AB=AC求证:∠B=?C分析:1.如何证明两个角相等? 2.如何构造两个全等的三角形?性质1(等边对等角)猜想⒈等腰三角形一个底角为75°,它的另外两个
角为_____ __;
⒉等腰三角形一个角为70°,它的另外两个角
为___________________;
⒊等腰三角形一个角为110°,它的另外两个角
为______ __。75°, 30°70°,40°或55°,55°35°,35°小试牛刀想一想: 刚才的证明除了能得到∠B=∠C 你还能发现什么?
A B D C AB=AC BD=CD AD=AD ∠B = ∠C.∠BAD = ∠CAD ∠ADB =∠ADC=90°等腰三角形顶角的平分线平分底边并且垂直于底边.性质2(等腰三角形三线合一)练习:选一选:1.(13年钦州)等腰三角形的一个角是80°,则它的顶角度数是( )
A.80° B.80°或20° C.80°或50° D.20°
2.(13年南充)在△ABC中,AB=AC,∠B=70°,则∠A=( )
A.70° B.55° C.50° D.40°
3.已知等腰三角形的一个内角为70°,则另外两个内角的度数是( )
A.55°,55° B.70°,40° C.55°,55°,或70°,40° D.以上都不对
如图:△ABC中,AB=AC。
(1)若AD平分∠BAC,则∠BDA= ,
BD= 。
(2)若BD=CD,则AD平分 ,
∠ADC=
(3)若AD⊥BC,则∠BAD= ,BC=2( )动手做一做ABCD如图,三角形ABC中,AC=BC,CD是∠ACB的平分线,AD=4cm,求AB的长及∠CDB的大小。CABD 轴对称图形两个底角相等,简称“等边对等角”顶角平分线、底边上的中线、和底边上的高
互相重合,简称“三线合 一”等腰三角形小 结性质1 : 等腰三角形的两个底角相等 (简称“等边对等角”,前提是在同一个三角形中。) 性质2 : 等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合。 (简称“三线合一”,前提是在同一个等腰三角形中。)
布置作业 1、预习课本P77-79,《名师大课堂》41页课前预习
2、书面作业:P81第1、3、4、7题,名师点拨本节练习谢谢指导再 见
