轴对称复习-等腰三角形[下学期]
文档属性
| 名称 | 轴对称复习-等腰三角形[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 471.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-18 21:02:00 | ||
图片预览




文档简介
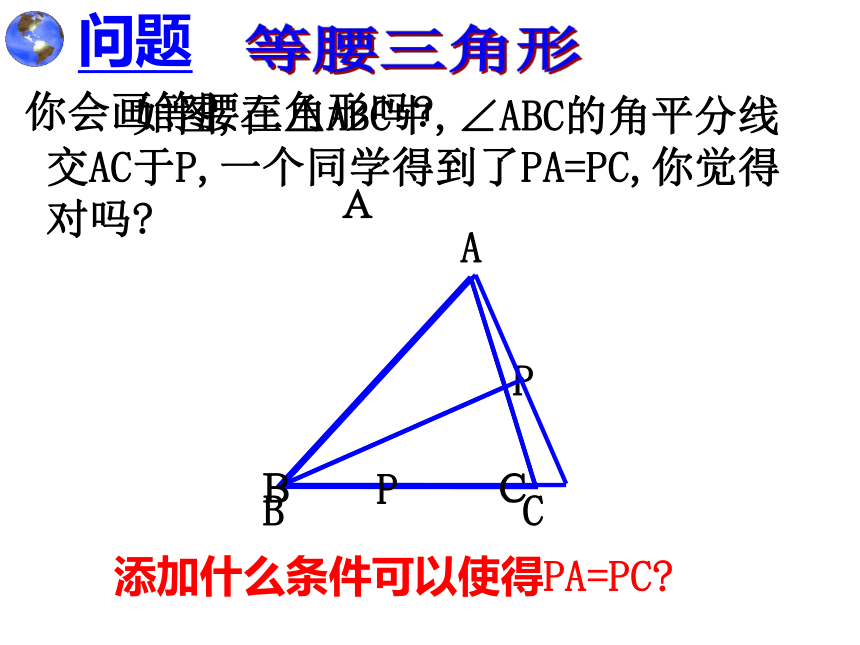
课件14张PPT。轴对称的回顾与思考等腰三角形执教者 市三中 江建军节选自人教版八年级上册 20世纪著名数学家赫尔曼·外 尔所说的,“对称是一种思想,人们毕生追求,并创造次序、美丽和完善……” 如图,在△ABC中,∠ABC的角平分线交AC于P,一个同学得到了PA=PC,你觉得对吗? 问题添加什么条件可以使得PA=PC?等腰三角形你会画等腰三角形吗?等腰三角形你会画等腰三角形吗?有两边相等的三角形是等腰三角形。性质定理1 :
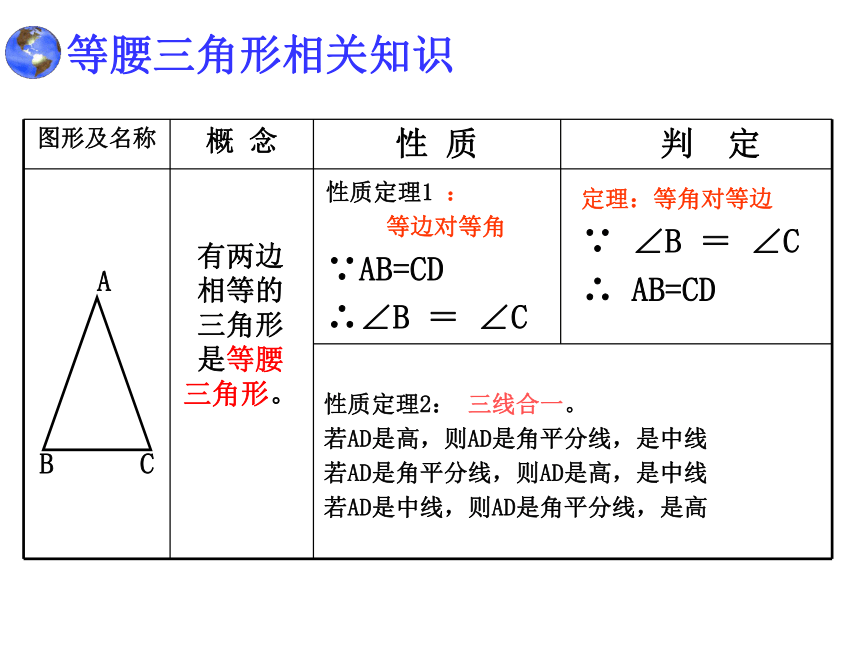
等边对等角
∵AB=CD
∴∠B = ∠C性质定理2: 三线合一。
若AD是高,则AD是角平分线,是中线
若AD是角平分线,则AD是高,是中线
若AD是中线,则AD是角平分线,是高定理:等角对等边
∵ ∠B = ∠C
∴ AB=CD等腰三角形相关知识∵ AB=AC, AD ⊥ BC∵ AB=AC , ∠1=∠2“三线合一”的数学语言(3)若AD是高,则AD是角平分线,是中线(1)若AD是角平分线,则AD是高,是中线(2) 若AD是中线,则AD是角平分线,是高∵ AB=AC, BD=CDAB=AC(3) 如图点E,请在AD上找一点P,使得
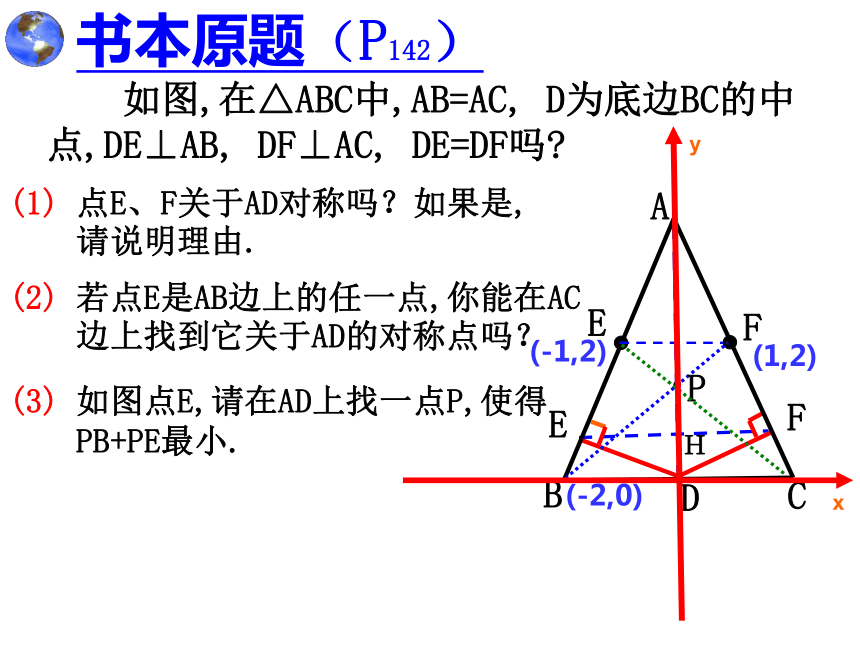
PB+PE最小. 如图,在△ABC中,AB=AC, D为底边BC的中点,DE⊥AB, DF⊥AC, DE=DF吗? 书本原题(P142)CDBA(1) 点E、F关于AD对称吗?如果是,
请说明理由. (2) 若点E是AB边上的任一点,你能在AC
边上找到它关于AD的对称点吗? (-2,0)(-1,2)(1,2)H 如图,在△ABC中,AB=AC, D为底边BC的中点. 书本原题(P142)变式1:平移直线AD,使得它与AB交于点E,
与CA的延长线交于点F,则AE=AF吗? EF 如图,在△ABC中,AB=AC, D为底边BC的中点. 书本原题(P142)CDBA变式1:平移直线AD,使得它与AB交于点E,
与CA的延长线交于点F,则AE=AF吗? EFH角平分线+平行线三角形中角的2倍关系构成等腰三角形的基本图形 如图,在△ABC中,AB=AC, D为底边BC的中点. 书本原题(P142)CDBA变式1:平移直线AD,使得它与AB交于点E,
与CA的延长线交于点F,则AE=AF吗? EFH变式2:继续平移FH至如图形状, AE=AF仍成立吗? 对于Rt△FBC来说,你还
能发现什么结论吗? 变式3:若FE刚好移至如图形状, AE(AB)=AF仍成立吗? 如图,在△ABC中,AB=AC, D为底边BC的中点. 书本原题(P142)CDBA变式1:平移直线AD,使得它与AB交于点E,
与CA的延长线交于点F,则AE=AF吗? EF变式2:继续平移FH至如图形状, AE=AF仍成立吗? 直角三角形斜边上的
中线等于斜边的一半. ∠C>∠B.如图,在△ABC中, 求证: AB>AC, 拓广探索DBACEF同一个三角形中,大边对大角,小边对小角.D 课堂小结
再见
等边对等角
∵AB=CD
∴∠B = ∠C性质定理2: 三线合一。
若AD是高,则AD是角平分线,是中线
若AD是角平分线,则AD是高,是中线
若AD是中线,则AD是角平分线,是高定理:等角对等边
∵ ∠B = ∠C
∴ AB=CD等腰三角形相关知识∵ AB=AC, AD ⊥ BC∵ AB=AC , ∠1=∠2“三线合一”的数学语言(3)若AD是高,则AD是角平分线,是中线(1)若AD是角平分线,则AD是高,是中线(2) 若AD是中线,则AD是角平分线,是高∵ AB=AC, BD=CDAB=AC(3) 如图点E,请在AD上找一点P,使得
PB+PE最小. 如图,在△ABC中,AB=AC, D为底边BC的中点,DE⊥AB, DF⊥AC, DE=DF吗? 书本原题(P142)CDBA(1) 点E、F关于AD对称吗?如果是,
请说明理由. (2) 若点E是AB边上的任一点,你能在AC
边上找到它关于AD的对称点吗? (-2,0)(-1,2)(1,2)H 如图,在△ABC中,AB=AC, D为底边BC的中点. 书本原题(P142)变式1:平移直线AD,使得它与AB交于点E,
与CA的延长线交于点F,则AE=AF吗? EF 如图,在△ABC中,AB=AC, D为底边BC的中点. 书本原题(P142)CDBA变式1:平移直线AD,使得它与AB交于点E,
与CA的延长线交于点F,则AE=AF吗? EFH角平分线+平行线三角形中角的2倍关系构成等腰三角形的基本图形 如图,在△ABC中,AB=AC, D为底边BC的中点. 书本原题(P142)CDBA变式1:平移直线AD,使得它与AB交于点E,
与CA的延长线交于点F,则AE=AF吗? EFH变式2:继续平移FH至如图形状, AE=AF仍成立吗? 对于Rt△FBC来说,你还
能发现什么结论吗? 变式3:若FE刚好移至如图形状, AE(AB)=AF仍成立吗? 如图,在△ABC中,AB=AC, D为底边BC的中点. 书本原题(P142)CDBA变式1:平移直线AD,使得它与AB交于点E,
与CA的延长线交于点F,则AE=AF吗? EF变式2:继续平移FH至如图形状, AE=AF仍成立吗? 直角三角形斜边上的
中线等于斜边的一半. ∠C>∠B.如图,在△ABC中, 求证: AB>AC, 拓广探索DBACEF同一个三角形中,大边对大角,小边对小角.D 课堂小结
再见
