人教版七年级数学上册第一章有理数 1.2有理数课件 (52张PPT)
文档属性
| 名称 | 人教版七年级数学上册第一章有理数 1.2有理数课件 (52张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 679.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-11 11:40:10 | ||
图片预览









文档简介
(共52张PPT)
有理数
问题导入
思考:
我们从小学开始,到现在学过哪些数?它们可以进行怎样的分类?
整数
正整数
0
负整数
分数
正分数
负分数
知识讲解
整数和分数统称为有理数.
知识讲解
注意:
1.有限小数和无限循环小数都可视为分数.
2.无限不循环小数不能化为分数,它不是有理数,例如:
知识讲解
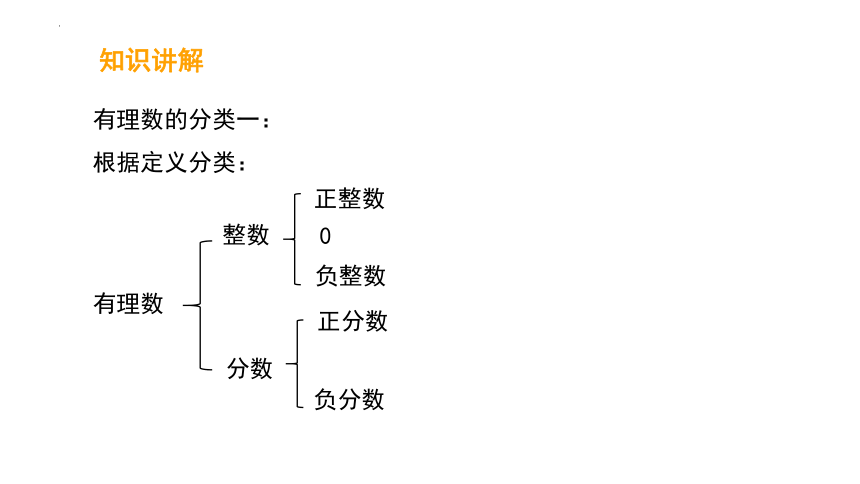
有理数的分类一:
根据定义分类:
整数
正整数
0
负整数
分数
正分数
负分数
有理数
知识讲解
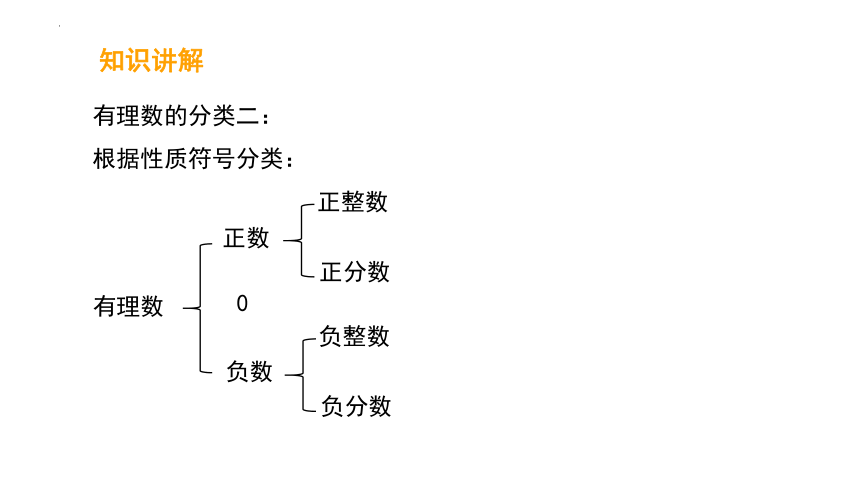
有理数的分类二:
根据性质符号分类:
正数
正整数
0
正分数
负数
有理数
负整数
负分数
注意:
非负分数是指正分数
非负整数是指正整数和0
非正数是指负数和0
非负数是指正数和0
分数和小数的区别:有限小数和无限循环小数可以化成分数,属于有理数。
下列说法正确的是( )
A.整数包括正整数和负整数
B.分数包括正分数和负分数
C.正有理数和负有理数组成全体有理数
D.一个数不是正数就是负数
例题1
练习1
下列说法中正确的是( )
A.正、负数统称为有理数
B.有理数分为整数、分数、正有理数、负有理数和0五大类
C.一个有理数不是整数就是分数
D.整数包括正整数、负整数
下列说法正确的是( )
A.零是正数不是负数
B.零既不是正数也不是负数
C.零既是正数也是负数
D.不是正数的数一定是负数
练习2
练习3
判断对错:
非负分数是指负整数、正整数和正分数 ( )
非负整数包括正整数和零。 ( )
非负分数包括正分数和零。 ( )
非正数就是负数。 ( )
有理数包括整数和分数,而分数可以化成小数,所以小数也是有理数。 ( )
在下列数中,属于负整数的是( )
A.3 B.-2 C.0 D.﹣1.5
例题2
练习1
下列各数:6,0,﹣8.25,﹣0.4,9,﹣,﹣28中,负有理数有( )个。
A.1个 B.2个 C.3个 D.4个
练习2
下列四个数中,既是分数又是正有理数的是( )
A.+2 B.﹣ C.0 D. 2.016
1.整数和分数统称为有理数.
2.对于有理数的分类,应遵循以下原则:
(1)分类不重合
(2)分类无遗漏
(3)标准要统一
要点总结
数 轴
定义:规定了原点、正方向和单位长度的长度的直线叫做数轴。
三要素:原点、正方向和单位长度。
数轴上的点与有理数的关系
所有有理数都可以用数轴上的一个点来表示,但数轴上的点并不 都是有理数。
用数轴比较大小
数轴上两个点表示的数,右边的总比左边的大。
正数大于0,负数小于0,正数大于负数。
原点右边的数都表示正数,原点左边的数表示负数,零用原点表示。
知识讲解
下面给出的四条数轴中画得正确的是( )
A. B.
C. D.
例题3
练习
下列说法正确的是( )
任何一个有理数都可以用数轴上的一个点来表示
规定了原点、正方向和单位长度的射线叫做数轴
C. 数轴上两个不同的点可以表示同一个有理数
D. 数轴上的每个点都对应一个有理数
例题4
如图所示,表示a、b、c在数轴上的位置,下列判断正确的是( )
A. a>b>c B. c>a>b C. a>c>b D. c>b>a
如图,根据实数 b,c,d在数轴上的位置判断,其中最大的数是________.
练习1
练习2
实数 、b在数轴上的位置如图所示,则下列式子成立的是( )
A. +b>0 B. >-b C. +b<0 D. -练习3
把下列各数在数轴上表示出来,井用“<”连接:
-1,1.5,-3,﹣2,0
在﹣1,﹣2,0,1四个数中最小的数是( )
A. ﹣1 B. ﹣2 C. 0 D. 1
例题5
练习1
数轴上点A表示2,点B表示﹣3,那么点_____距离原点比较近。
比较大小:0_____﹣1; -2_____-3 ;﹣ _____-
在下列四个数中,最大的数是( )
A.﹣4 B.0 C.﹣1 D.3
练习2
数轴上A,B,C三点所对应的实数分别为﹣,则此三点按从小到大的顺序为____________________.
例题6
在数轴上,表示+4的点在原点的____侧,距原点____个单位.
练习1
数轴上表示一个数的点与原点的距离是6,那么这个数是______.
练习2
如图,在数轴上与A点的距离等于5的数为_________。
练习3
在数轴上,到原点的距离不大于3的点所表示的整数有哪些?
相 反 数
知识讲解
定义:只有符号不同的两个数,我们说其中一个数是另一个数的相反数,也称这两个数互为相反数。
表示方法:要表示一个数的相反数,只要在这个数的前面添上一个“-”号就可以。例如,的相反数是.
几何意义:在数轴上原点的两侧,与原点距离相等的两个点所表示的数,就互为相反数。
性质:任何一个数都有相反数,而且只有一个。正数的相反数一定是负数;负数的相反数一定是正数;0的相反数仍是0.
理解相反数的定义注意:
相反数是成对出现的,不能单独存在。单独的一个数不能说是相反数。
“只有符号不同的两个数”中的“只有”,指的是除了符号不同以外其余完全相同,不能理解为只要符号不同的两个数就互为相反数。
求一个数的相反数的方法就是在这个数的前边添加“-”。
如a的相反数是-a;m+n的相反数是-(m+n),这时m+n是一个整体,在整体前面添负号时,要用小括号.
知识讲解
下列说法正确的是( )
A.符号相反的数就是相反数
B.每个有理数都有相反数
C.互为相反数的两个数一定不相等
D.正数和负数互为相反数
例题1
练习
2的相反数是______.
-5的相反数是______.
的相反数是______.
-的相反数是______.
3+m的相反数是__________.
-(-2)的相反数是________.
练习2
如图所示,数轴上点A所表示的数的相反数是___.
在如图,数轴上有A、B、C、D四个点,其中表示互为相反数的点是( )
A.点A与点D
B.点A与点C
C.点B与点D
D.点B与点C
练习3
绝 对 值
知识讲解
定义:一般地,数轴上表示数与原点的距离叫做数的绝对值,记作||.
意义
代数意义
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0的绝对值是0.
用字母表示为||=
几何意义:
在数轴上,表示数与原点的距离,叫做数的绝对值
非负性
知识讲解
利用绝对值比较大小:
两数同号
同为异号:正数大于负号
数轴上表示2的点到原点的距离是_____,所以|2|=_______.
数轴上表示-2的点到原点的距离是____,所以|-2|=_______.
数轴上表示0的点到原点的距离是_____,所以|0|=_______.
例题2
练习
4的绝对值是______.
﹣2的绝对值是______.
的绝对值是______.
|﹣6|的绝对值是________.
-|-2|的绝对值是________.
当 <0时,化简等于( )
A.1 B.-1 C.0 D.
例题3
如果,那么的取值范围是( )
A. >0 B. C. D. <0
若||=4,则=_______.
若| |=|﹣3|,则 =_______.
练习
若|m-1|+|n-2|=0,则m=_____,n=_____.
例题4
若|-2022|+| |=0,则+y=_______.
练习
计算:
(1)0.3+|﹣0.2| (2)1-|﹣|
(3)|-1.2|+|﹣2.7| (4)|-8|-|﹣2.5|
例题5
计算:
(1)0.3×|﹣0.2| (2)6÷|﹣|
(3)|-12|×|0.5| (4)|-8|÷|﹣|
练习
2的相反数和绝对值分别是( )
A、2,2 B、-2,2 C、-2,-2 D、2,-2
例题6
下面各组中,互为相反数的是( )
A、|-2|与|2|
B、-|+2|与|-2|
C、-(+2)与+(-2)
D、-(-2)与+(+2)
练习1
若x的相反数是3,|y|=5,则x+y的值为( )
A、-8 B、2 C、8或-2 D、-8或2
练习2
课堂总结
有理数
有理数的定义及其分类
数轴
相反数
绝对值
有理数
问题导入
思考:
我们从小学开始,到现在学过哪些数?它们可以进行怎样的分类?
整数
正整数
0
负整数
分数
正分数
负分数
知识讲解
整数和分数统称为有理数.
知识讲解
注意:
1.有限小数和无限循环小数都可视为分数.
2.无限不循环小数不能化为分数,它不是有理数,例如:
知识讲解
有理数的分类一:
根据定义分类:
整数
正整数
0
负整数
分数
正分数
负分数
有理数
知识讲解
有理数的分类二:
根据性质符号分类:
正数
正整数
0
正分数
负数
有理数
负整数
负分数
注意:
非负分数是指正分数
非负整数是指正整数和0
非正数是指负数和0
非负数是指正数和0
分数和小数的区别:有限小数和无限循环小数可以化成分数,属于有理数。
下列说法正确的是( )
A.整数包括正整数和负整数
B.分数包括正分数和负分数
C.正有理数和负有理数组成全体有理数
D.一个数不是正数就是负数
例题1
练习1
下列说法中正确的是( )
A.正、负数统称为有理数
B.有理数分为整数、分数、正有理数、负有理数和0五大类
C.一个有理数不是整数就是分数
D.整数包括正整数、负整数
下列说法正确的是( )
A.零是正数不是负数
B.零既不是正数也不是负数
C.零既是正数也是负数
D.不是正数的数一定是负数
练习2
练习3
判断对错:
非负分数是指负整数、正整数和正分数 ( )
非负整数包括正整数和零。 ( )
非负分数包括正分数和零。 ( )
非正数就是负数。 ( )
有理数包括整数和分数,而分数可以化成小数,所以小数也是有理数。 ( )
在下列数中,属于负整数的是( )
A.3 B.-2 C.0 D.﹣1.5
例题2
练习1
下列各数:6,0,﹣8.25,﹣0.4,9,﹣,﹣28中,负有理数有( )个。
A.1个 B.2个 C.3个 D.4个
练习2
下列四个数中,既是分数又是正有理数的是( )
A.+2 B.﹣ C.0 D. 2.016
1.整数和分数统称为有理数.
2.对于有理数的分类,应遵循以下原则:
(1)分类不重合
(2)分类无遗漏
(3)标准要统一
要点总结
数 轴
定义:规定了原点、正方向和单位长度的长度的直线叫做数轴。
三要素:原点、正方向和单位长度。
数轴上的点与有理数的关系
所有有理数都可以用数轴上的一个点来表示,但数轴上的点并不 都是有理数。
用数轴比较大小
数轴上两个点表示的数,右边的总比左边的大。
正数大于0,负数小于0,正数大于负数。
原点右边的数都表示正数,原点左边的数表示负数,零用原点表示。
知识讲解
下面给出的四条数轴中画得正确的是( )
A. B.
C. D.
例题3
练习
下列说法正确的是( )
任何一个有理数都可以用数轴上的一个点来表示
规定了原点、正方向和单位长度的射线叫做数轴
C. 数轴上两个不同的点可以表示同一个有理数
D. 数轴上的每个点都对应一个有理数
例题4
如图所示,表示a、b、c在数轴上的位置,下列判断正确的是( )
A. a>b>c B. c>a>b C. a>c>b D. c>b>a
如图,根据实数 b,c,d在数轴上的位置判断,其中最大的数是________.
练习1
练习2
实数 、b在数轴上的位置如图所示,则下列式子成立的是( )
A. +b>0 B. >-b C. +b<0 D. -
把下列各数在数轴上表示出来,井用“<”连接:
-1,1.5,-3,﹣2,0
在﹣1,﹣2,0,1四个数中最小的数是( )
A. ﹣1 B. ﹣2 C. 0 D. 1
例题5
练习1
数轴上点A表示2,点B表示﹣3,那么点_____距离原点比较近。
比较大小:0_____﹣1; -2_____-3 ;﹣ _____-
在下列四个数中,最大的数是( )
A.﹣4 B.0 C.﹣1 D.3
练习2
数轴上A,B,C三点所对应的实数分别为﹣,则此三点按从小到大的顺序为____________________.
例题6
在数轴上,表示+4的点在原点的____侧,距原点____个单位.
练习1
数轴上表示一个数的点与原点的距离是6,那么这个数是______.
练习2
如图,在数轴上与A点的距离等于5的数为_________。
练习3
在数轴上,到原点的距离不大于3的点所表示的整数有哪些?
相 反 数
知识讲解
定义:只有符号不同的两个数,我们说其中一个数是另一个数的相反数,也称这两个数互为相反数。
表示方法:要表示一个数的相反数,只要在这个数的前面添上一个“-”号就可以。例如,的相反数是.
几何意义:在数轴上原点的两侧,与原点距离相等的两个点所表示的数,就互为相反数。
性质:任何一个数都有相反数,而且只有一个。正数的相反数一定是负数;负数的相反数一定是正数;0的相反数仍是0.
理解相反数的定义注意:
相反数是成对出现的,不能单独存在。单独的一个数不能说是相反数。
“只有符号不同的两个数”中的“只有”,指的是除了符号不同以外其余完全相同,不能理解为只要符号不同的两个数就互为相反数。
求一个数的相反数的方法就是在这个数的前边添加“-”。
如a的相反数是-a;m+n的相反数是-(m+n),这时m+n是一个整体,在整体前面添负号时,要用小括号.
知识讲解
下列说法正确的是( )
A.符号相反的数就是相反数
B.每个有理数都有相反数
C.互为相反数的两个数一定不相等
D.正数和负数互为相反数
例题1
练习
2的相反数是______.
-5的相反数是______.
的相反数是______.
-的相反数是______.
3+m的相反数是__________.
-(-2)的相反数是________.
练习2
如图所示,数轴上点A所表示的数的相反数是___.
在如图,数轴上有A、B、C、D四个点,其中表示互为相反数的点是( )
A.点A与点D
B.点A与点C
C.点B与点D
D.点B与点C
练习3
绝 对 值
知识讲解
定义:一般地,数轴上表示数与原点的距离叫做数的绝对值,记作||.
意义
代数意义
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0的绝对值是0.
用字母表示为||=
几何意义:
在数轴上,表示数与原点的距离,叫做数的绝对值
非负性
知识讲解
利用绝对值比较大小:
两数同号
同为异号:正数大于负号
数轴上表示2的点到原点的距离是_____,所以|2|=_______.
数轴上表示-2的点到原点的距离是____,所以|-2|=_______.
数轴上表示0的点到原点的距离是_____,所以|0|=_______.
例题2
练习
4的绝对值是______.
﹣2的绝对值是______.
的绝对值是______.
|﹣6|的绝对值是________.
-|-2|的绝对值是________.
当 <0时,化简等于( )
A.1 B.-1 C.0 D.
例题3
如果,那么的取值范围是( )
A. >0 B. C. D. <0
若||=4,则=_______.
若| |=|﹣3|,则 =_______.
练习
若|m-1|+|n-2|=0,则m=_____,n=_____.
例题4
若|-2022|+| |=0,则+y=_______.
练习
计算:
(1)0.3+|﹣0.2| (2)1-|﹣|
(3)|-1.2|+|﹣2.7| (4)|-8|-|﹣2.5|
例题5
计算:
(1)0.3×|﹣0.2| (2)6÷|﹣|
(3)|-12|×|0.5| (4)|-8|÷|﹣|
练习
2的相反数和绝对值分别是( )
A、2,2 B、-2,2 C、-2,-2 D、2,-2
例题6
下面各组中,互为相反数的是( )
A、|-2|与|2|
B、-|+2|与|-2|
C、-(+2)与+(-2)
D、-(-2)与+(+2)
练习1
若x的相反数是3,|y|=5,则x+y的值为( )
A、-8 B、2 C、8或-2 D、-8或2
练习2
课堂总结
有理数
有理数的定义及其分类
数轴
相反数
绝对值
