11.2.1三角形的内角 同步练习题(含答案)
文档属性
| 名称 | 11.2.1三角形的内角 同步练习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-10 17:57:35 | ||
图片预览


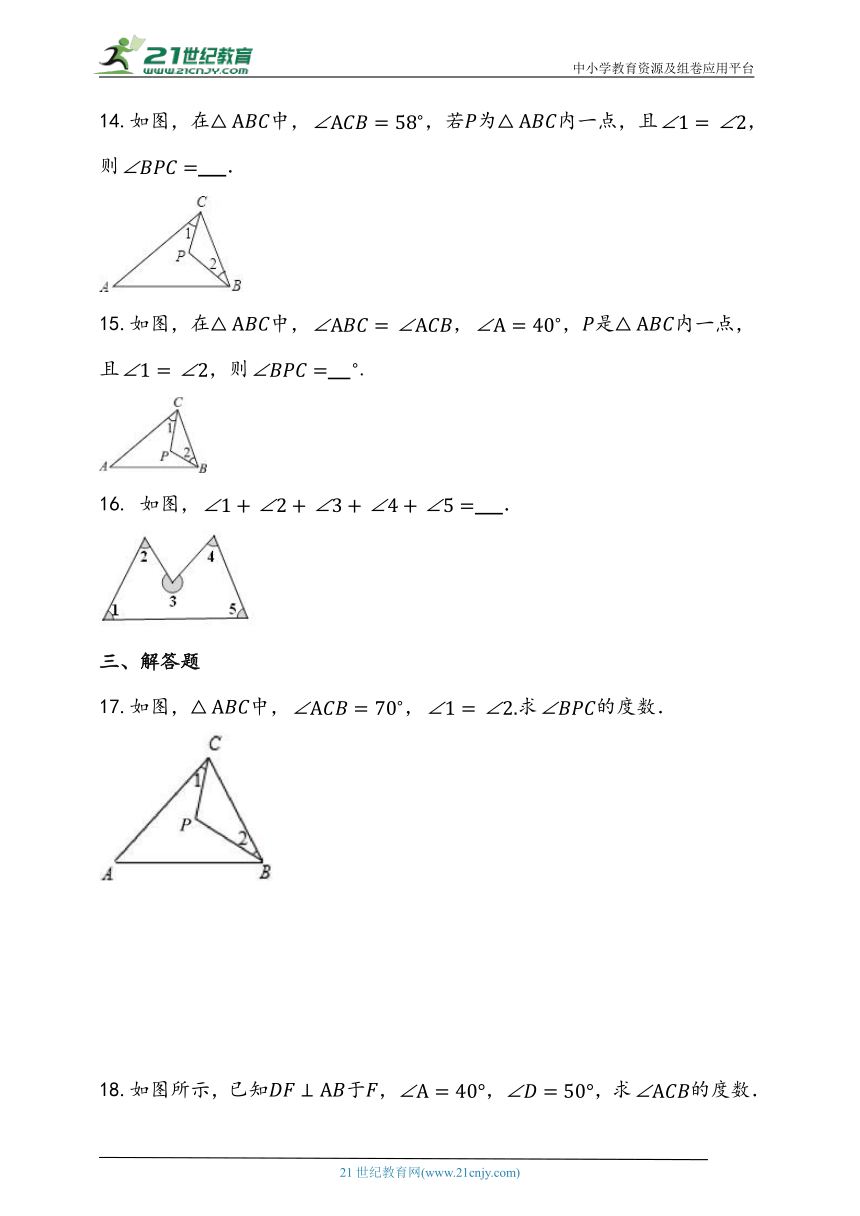

文档简介
中小学教育资源及组卷应用平台
11.2.1三角形的内角
学校:______姓名:______班级:______考号:______
一、单选题
1.如果直角三角形的一个锐角的度数是,那么另一个锐角的度数是()
A. B. C. D.
2.如图,三角形被遮住的两个角不可能是( )
A.一个锐角,一个钝角 B.两个锐角
C.一个锐角,一个直角 D.两个钝角
3.在中,,,则的度数为( )
A. B. C. D.或
4.在中,已知,则的度数是( )
A. B. C. D.
5.在三个内角互不相等的中,最小的内角为,则在下列四个度数中,最大可取( )
A. B. C. D.
6.下列性质中,直角三角形具有而等腰三角形不一定具有的是( )
A.两边之和大于第三边
B.内角和等于
C.有两个锐角的和等于
D.有一个角的平分线垂直于这个角的对边
7.在一个三角形的三个内角中,说法正确的是( )
A.至少有一个直角 B.至少有一个钝角
C.至多有两个锐角 D.至少有两个锐角
8.如图,△ABC中,∠A=45°,点D、E分别在AB、AC上,则∠1+∠2的大小为( )
A.225° B.135° C.180° D.315°
二、填空题
9.如图,已知是射线上一动点,当为直角三角形时的度数为 .
10.在中,,那么= °.
11.如图,中,,,则 .
12.在中,,,则 .
13.在中,,,则 .
14.如图,在中,,若为内一点,且,则 .
15.如图,在中,,,是内一点,且,则 .
16. 如图, .
三、解答题
17.如图,中,,求的度数.
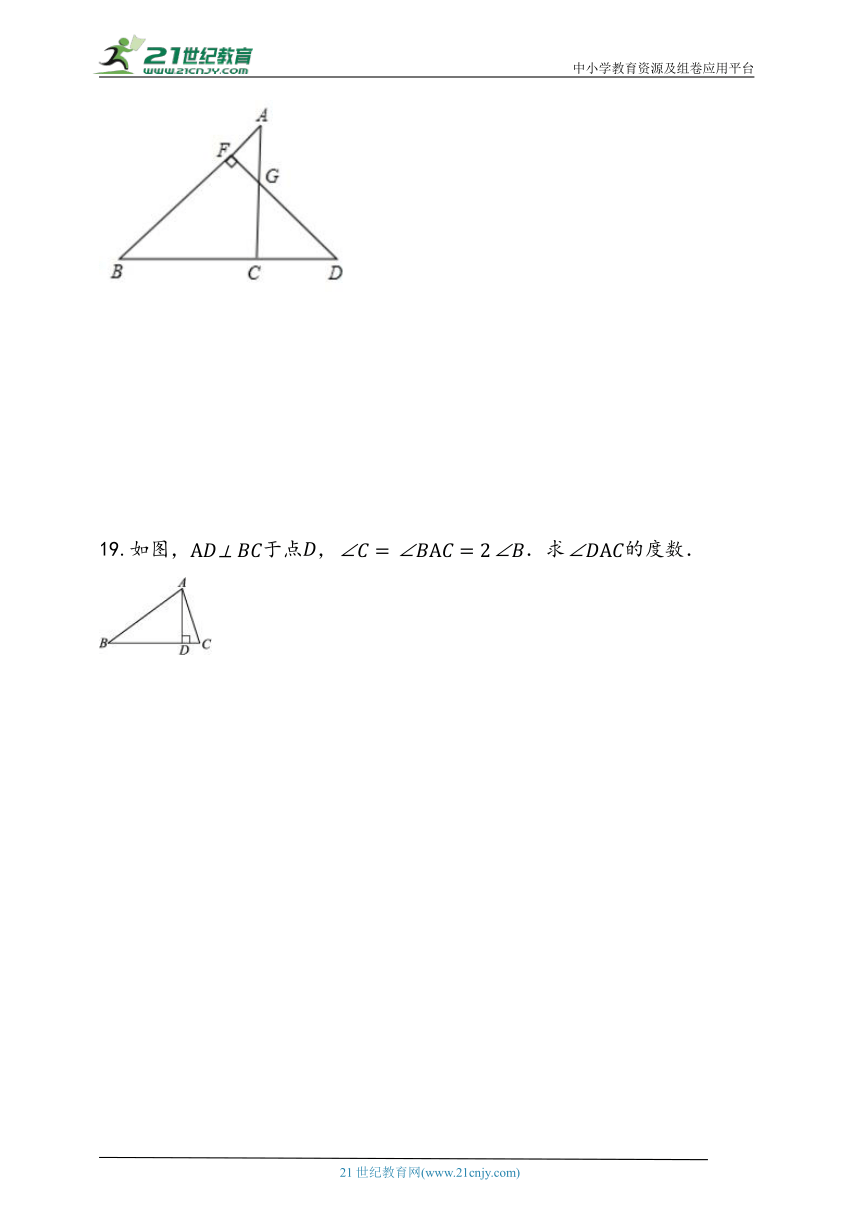
18.如图所示,已知于,,,求的度数.
19.如图,于点,.求的度数.
参考答案
1.【答案】B
2.【答案】D
【解析】因为三角形内角之和为,所以三角形被遮住的两个角不可能是两个钝角.
故选D.
3.【答案】A
【解析】在中,,,
,.故选.
4.【答案】A
【解析】根据已知条件求出的度数,再根据三角形的内角和等于列式计算即可得解.
解:,
,
.
故选.
本题考查了三角形的内角和定理,是基础题,求出的度数,然后列出的表达式是解题的关键.
5.【答案】B
【解析】∵,
而不等边三角形的最小内角为,
∴,
∴,
故四个度数中,最大可取
6.【答案】C
【解析】项,对于任意一个三角形都有两边之和大于第三边,不符合题意;
项,对于任意一个三角形都有内角和等于,不符合题意;
项,只有直角三角形才有两个锐角的和等于,符合题意;
项,等腰三角形顶角的平分线垂直于顶角的对边,而直角三角形(等腰直角三角形除外)没有任何一个角的平分线垂直于这个角的对边,不符合题意.
故选.
7.【答案】D
【解析】根据内角和定理解题.如有两个或两个以上的直角、钝角就会和内角和定理矛盾了.
故选D.
8.【答案】A
【解析】根据三角形的外角性质可得∠1=∠A+∠ADE,∠2=∠A+∠AED,再根据已知和三角形内角和等于180°即可求解.
∵∠1=∠A+∠ADE,∠2=∠A+∠AED,
∴∠1+∠2
=∠A+∠ADE+∠A+∠AED
=∠A+(∠ADE+∠A+∠AED)
=45°+180°
=225°.
故选A.
9.【答案】或
【解析】当时则;当时即当为直角三角形时或.
10.【答案】67.5
【解析】由可知,, 所以.
11.【答案】
【解析】,
.
,
,
.
故答案为.
12.【答案】
【解析】∵,且,,
∴(),
据此可知答案为:.
根据题目的已知条件,利用三角形的内角和外角的相关知识可以得到问题的答案,需要掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.
13.【答案】
14.【答案】
【解析】∵,又∵,
∴,
∵,
∴.
所以答案是.
解答此题的关键在于理解三角形的内角和外角的相关知识,掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.
15.【答案】
【解析】∵,, ∴. ∵, ∴, ∴在中,.
16.【答案】
【解析】【分析】
本题主要考查三角形的内角和为定理,需作辅助线,比较简单.连接和,和的顶点,可得三个三角形,根据三角形的内角和定理即可求出答案.
【解答】
解:连接和,和的顶点,可得三个三角形,
根据三角形的内角和定理,.
故答案为.
17.【答案】解:,,
又,
,
在中,
,
,
,
.
【解析】本题考查的是三角形内角和定理,熟知三角形内角和是是解答此题的关键由和得出的度数为,根据三角形内角和定理即可得出结论.
18.【答案】在中,,
在中,,
故.
【解析】根据三角形的内角和定理,先在中求出的度数,然后在中求出的度数.
19.【答案】解:设,则,
,
,
,
.
在中,.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
11.2.1三角形的内角
学校:______姓名:______班级:______考号:______
一、单选题
1.如果直角三角形的一个锐角的度数是,那么另一个锐角的度数是()
A. B. C. D.
2.如图,三角形被遮住的两个角不可能是( )
A.一个锐角,一个钝角 B.两个锐角
C.一个锐角,一个直角 D.两个钝角
3.在中,,,则的度数为( )
A. B. C. D.或
4.在中,已知,则的度数是( )
A. B. C. D.
5.在三个内角互不相等的中,最小的内角为,则在下列四个度数中,最大可取( )
A. B. C. D.
6.下列性质中,直角三角形具有而等腰三角形不一定具有的是( )
A.两边之和大于第三边
B.内角和等于
C.有两个锐角的和等于
D.有一个角的平分线垂直于这个角的对边
7.在一个三角形的三个内角中,说法正确的是( )
A.至少有一个直角 B.至少有一个钝角
C.至多有两个锐角 D.至少有两个锐角
8.如图,△ABC中,∠A=45°,点D、E分别在AB、AC上,则∠1+∠2的大小为( )
A.225° B.135° C.180° D.315°
二、填空题
9.如图,已知是射线上一动点,当为直角三角形时的度数为 .
10.在中,,那么= °.
11.如图,中,,,则 .
12.在中,,,则 .
13.在中,,,则 .
14.如图,在中,,若为内一点,且,则 .
15.如图,在中,,,是内一点,且,则 .
16. 如图, .
三、解答题
17.如图,中,,求的度数.
18.如图所示,已知于,,,求的度数.
19.如图,于点,.求的度数.
参考答案
1.【答案】B
2.【答案】D
【解析】因为三角形内角之和为,所以三角形被遮住的两个角不可能是两个钝角.
故选D.
3.【答案】A
【解析】在中,,,
,.故选.
4.【答案】A
【解析】根据已知条件求出的度数,再根据三角形的内角和等于列式计算即可得解.
解:,
,
.
故选.
本题考查了三角形的内角和定理,是基础题,求出的度数,然后列出的表达式是解题的关键.
5.【答案】B
【解析】∵,
而不等边三角形的最小内角为,
∴,
∴,
故四个度数中,最大可取
6.【答案】C
【解析】项,对于任意一个三角形都有两边之和大于第三边,不符合题意;
项,对于任意一个三角形都有内角和等于,不符合题意;
项,只有直角三角形才有两个锐角的和等于,符合题意;
项,等腰三角形顶角的平分线垂直于顶角的对边,而直角三角形(等腰直角三角形除外)没有任何一个角的平分线垂直于这个角的对边,不符合题意.
故选.
7.【答案】D
【解析】根据内角和定理解题.如有两个或两个以上的直角、钝角就会和内角和定理矛盾了.
故选D.
8.【答案】A
【解析】根据三角形的外角性质可得∠1=∠A+∠ADE,∠2=∠A+∠AED,再根据已知和三角形内角和等于180°即可求解.
∵∠1=∠A+∠ADE,∠2=∠A+∠AED,
∴∠1+∠2
=∠A+∠ADE+∠A+∠AED
=∠A+(∠ADE+∠A+∠AED)
=45°+180°
=225°.
故选A.
9.【答案】或
【解析】当时则;当时即当为直角三角形时或.
10.【答案】67.5
【解析】由可知,, 所以.
11.【答案】
【解析】,
.
,
,
.
故答案为.
12.【答案】
【解析】∵,且,,
∴(),
据此可知答案为:.
根据题目的已知条件,利用三角形的内角和外角的相关知识可以得到问题的答案,需要掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.
13.【答案】
14.【答案】
【解析】∵,又∵,
∴,
∵,
∴.
所以答案是.
解答此题的关键在于理解三角形的内角和外角的相关知识,掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.
15.【答案】
【解析】∵,, ∴. ∵, ∴, ∴在中,.
16.【答案】
【解析】【分析】
本题主要考查三角形的内角和为定理,需作辅助线,比较简单.连接和,和的顶点,可得三个三角形,根据三角形的内角和定理即可求出答案.
【解答】
解:连接和,和的顶点,可得三个三角形,
根据三角形的内角和定理,.
故答案为.
17.【答案】解:,,
又,
,
在中,
,
,
,
.
【解析】本题考查的是三角形内角和定理,熟知三角形内角和是是解答此题的关键由和得出的度数为,根据三角形内角和定理即可得出结论.
18.【答案】在中,,
在中,,
故.
【解析】根据三角形的内角和定理,先在中求出的度数,然后在中求出的度数.
19.【答案】解:设,则,
,
,
,
.
在中,.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
