11.2.2三角形的外角 同步练习题(含答案)
文档属性
| 名称 | 11.2.2三角形的外角 同步练习题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-10 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
11.2.2三角形的外角
学校:______姓名:______班级:______考号:______
一、单选题
1.下列说法正确的是( )
A.三角形的一个外角等于这个三角形的两个内角之和
B.三角形的一个外角小于它的一个内角
C.三角形的一个外角大于这个三角形的任何一个内角
D.三角形的一个外角与它相邻的内角互补
2.如果将一副三角尺按如图所示方式叠放,那么等于( )
A. B. C. D.
3.如图,已知则( )
A. B. C. D.
4.如图,已知,,,则的度数为( )
A. B. C. D.
5.如图所示,下列关系正确的是( )
A. B. C. D.
6.如图,在中若则的度数为( )
A. B. C. D.
7.如图,是的外角的平分线,,,则的度数是( )
A. B. C. D.
二、填空题
8.如图,已知则 .
9.如图,飞机要从地飞往地,因受大风影响,偏离航线即,飞到了地.已知,现在飞机要达到地需以 度角飞行(即的度数).
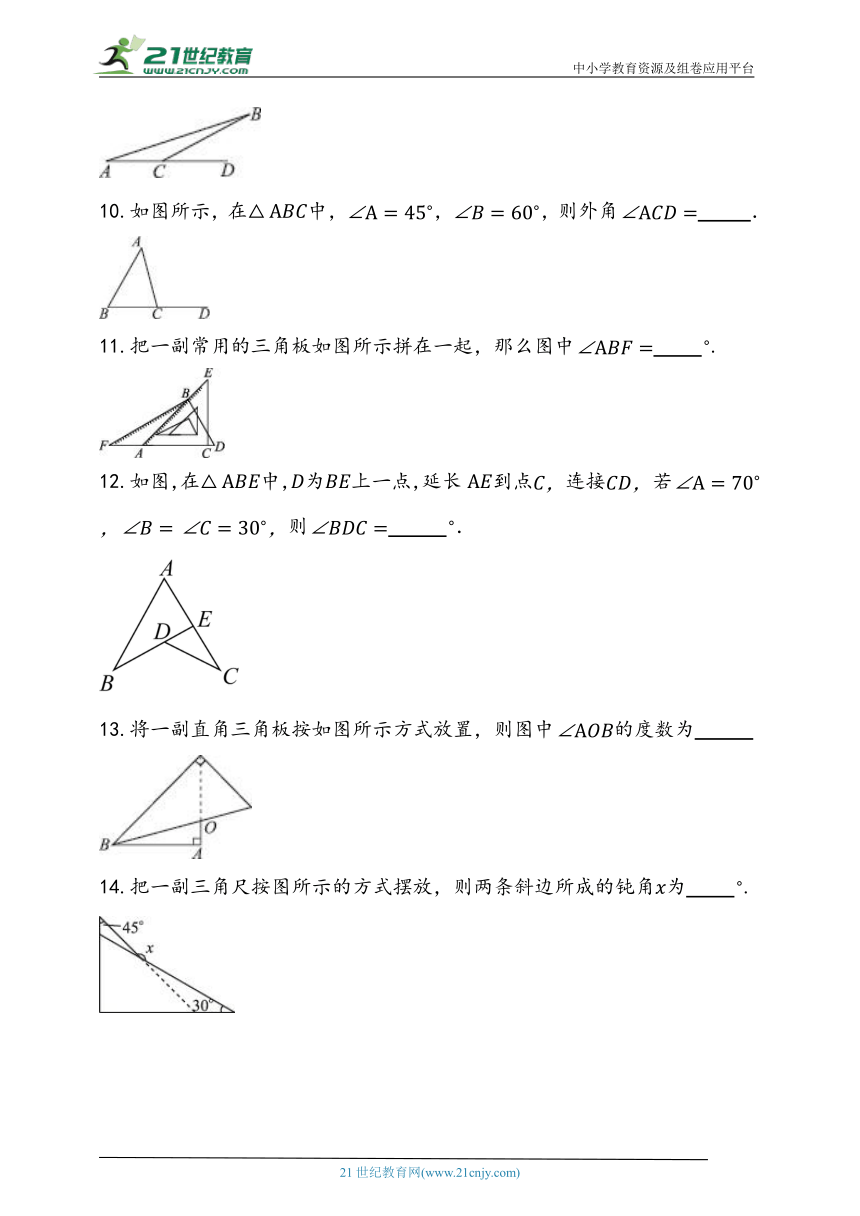
10.如图所示,在中,,,则外角 .
11.把一副常用的三角板如图所示拼在一起,那么图中 .
12.如图,在中,为上一点,延长到点连接若则 .
13.将一副直角三角板按如图所示方式放置,则图中的度数为
14.把一副三角尺按图所示的方式摆放,则两条斜边所成的钝角为 .
三、解答题
15.如图所示,在五角星中,试说明:.
16.两只猎豹在如图的处发现有一只野牛离群独自在处觅食,猎豹打算用迂回的方式捕猎,由一只先从前进到处,然后再折回到处截住野牛返回牛群的去路,另一只则直接从处扑向野牛,已知,,则猎豹从处要逆时针转多少度才能直达处?
17.如图,有两根竹竿,靠在墙角上,并与墙角形成一定的角度,测得,的度数分别为,,用含有,的代数式表示和的度数.
18.我们知道,三角形的一个外角等于与它不相邻的两个内角的和,那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢? 已知:如图,,为的两个外角,则与的数量关系为 .请证明你的结论.
19.解答下列问题:
(1)如图①是一只展翅飞翔的大雁的示意图,求证:;
(2)图②是一只嗷嗷待哺的小鸟的示意图,则 .
参考答案
1.【答案】D
【解析】考点分析:本题主要考查三角形的外角.
思路分析:根据三角形外角的性质解题.
选项分析:
项,三角形的一个外角等于这个三角形中不相邻的两个内角之和,故 项错误;
项,三角形的一个外角有可能与其相邻的内角相等,也有可能小于与其相邻的内角,也有可能大于与其相邻的内角,要分情况讨论,故项错误;
项,三角形的一个外角大于这个三角形的任何一个不相邻的内角,故项错误;
项,三角形的一个外角与它相邻的内角互补,故项正确.
故选:.
2.【答案】B
3.【答案】C
4.【答案】A
【解析】由三角形的一个外角等于与它不相邻的两个内角的和,得
,
同理,,
代入即可求解.
,,,
同理,,
.
故选A.
5.【答案】B
【解析】【分析】本题考查的是三角形外角性质有关知识,根据三角形内角和外角的关系解答即可.
【解答】解:∵是三角形的一个外角,而是此三角形的一个内角,且与不相邻,
∴.
故选.
6.【答案】C
【解析】,,,
.
故选.
7.【答案】C
【解析】∵,,
∴﹣﹣,
∴﹣﹣﹣﹣.
故选.
本题主要考查了三角形的外角和三角形的内角和外角的相关知识点,需要掌握三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角才能正确解答此题.
8.【答案】
9.【答案】
【解析】∵,,
∴.故答案为
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
【解析】.
15.【答案】证明:,,
又,
.
16.【答案】解:,,
.
答:猎豹从处要逆时针转才能直达处.
17.【答案】解:由三角形外角的性质可知
,,
.
18.【答案】解:.
证明:,,
.
,
,
即.
19.【答案】(1)证明:连接并延长,如图..
(2)
【解析】(2)根据题意,连接,如图.由的结论,易得,.,,.故答案为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
11.2.2三角形的外角
学校:______姓名:______班级:______考号:______
一、单选题
1.下列说法正确的是( )
A.三角形的一个外角等于这个三角形的两个内角之和
B.三角形的一个外角小于它的一个内角
C.三角形的一个外角大于这个三角形的任何一个内角
D.三角形的一个外角与它相邻的内角互补
2.如果将一副三角尺按如图所示方式叠放,那么等于( )
A. B. C. D.
3.如图,已知则( )
A. B. C. D.
4.如图,已知,,,则的度数为( )
A. B. C. D.
5.如图所示,下列关系正确的是( )
A. B. C. D.
6.如图,在中若则的度数为( )
A. B. C. D.
7.如图,是的外角的平分线,,,则的度数是( )
A. B. C. D.
二、填空题
8.如图,已知则 .
9.如图,飞机要从地飞往地,因受大风影响,偏离航线即,飞到了地.已知,现在飞机要达到地需以 度角飞行(即的度数).
10.如图所示,在中,,,则外角 .
11.把一副常用的三角板如图所示拼在一起,那么图中 .
12.如图,在中,为上一点,延长到点连接若则 .
13.将一副直角三角板按如图所示方式放置,则图中的度数为
14.把一副三角尺按图所示的方式摆放,则两条斜边所成的钝角为 .
三、解答题
15.如图所示,在五角星中,试说明:.
16.两只猎豹在如图的处发现有一只野牛离群独自在处觅食,猎豹打算用迂回的方式捕猎,由一只先从前进到处,然后再折回到处截住野牛返回牛群的去路,另一只则直接从处扑向野牛,已知,,则猎豹从处要逆时针转多少度才能直达处?
17.如图,有两根竹竿,靠在墙角上,并与墙角形成一定的角度,测得,的度数分别为,,用含有,的代数式表示和的度数.
18.我们知道,三角形的一个外角等于与它不相邻的两个内角的和,那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢? 已知:如图,,为的两个外角,则与的数量关系为 .请证明你的结论.
19.解答下列问题:
(1)如图①是一只展翅飞翔的大雁的示意图,求证:;
(2)图②是一只嗷嗷待哺的小鸟的示意图,则 .
参考答案
1.【答案】D
【解析】考点分析:本题主要考查三角形的外角.
思路分析:根据三角形外角的性质解题.
选项分析:
项,三角形的一个外角等于这个三角形中不相邻的两个内角之和,故 项错误;
项,三角形的一个外角有可能与其相邻的内角相等,也有可能小于与其相邻的内角,也有可能大于与其相邻的内角,要分情况讨论,故项错误;
项,三角形的一个外角大于这个三角形的任何一个不相邻的内角,故项错误;
项,三角形的一个外角与它相邻的内角互补,故项正确.
故选:.
2.【答案】B
3.【答案】C
4.【答案】A
【解析】由三角形的一个外角等于与它不相邻的两个内角的和,得
,
同理,,
代入即可求解.
,,,
同理,,
.
故选A.
5.【答案】B
【解析】【分析】本题考查的是三角形外角性质有关知识,根据三角形内角和外角的关系解答即可.
【解答】解:∵是三角形的一个外角,而是此三角形的一个内角,且与不相邻,
∴.
故选.
6.【答案】C
【解析】,,,
.
故选.
7.【答案】C
【解析】∵,,
∴﹣﹣,
∴﹣﹣﹣﹣.
故选.
本题主要考查了三角形的外角和三角形的内角和外角的相关知识点,需要掌握三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角才能正确解答此题.
8.【答案】
9.【答案】
【解析】∵,,
∴.故答案为
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
【解析】.
15.【答案】证明:,,
又,
.
16.【答案】解:,,
.
答:猎豹从处要逆时针转才能直达处.
17.【答案】解:由三角形外角的性质可知
,,
.
18.【答案】解:.
证明:,,
.
,
,
即.
19.【答案】(1)证明:连接并延长,如图..
(2)
【解析】(2)根据题意,连接,如图.由的结论,易得,.,,.故答案为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
