福建省漳州市2022-2023学年高二下学期期末教学质量检测数学试题(含答案)
文档属性
| 名称 | 福建省漳州市2022-2023学年高二下学期期末教学质量检测数学试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 943.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-11 00:00:00 | ||
图片预览




文档简介
漳州市2022-2023学年高二下学期期末教学质量检测
数学试题
(考试时间:120分钟满分:150分)
考生注意:
1.答题前,考生务必在试题卷 答题卡规定的地方填写自己的准考证号 姓名.考生要认真核对答题卡上粘贴的条形码的“准考证号 姓名”与考生本人准考证号 姓名是否一致.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.
3.考试结束,考生必须将试题卷和答题卡一并交回.
一 单项选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列导数运算正确的是( )
A. B.
C. D.
2.已知事件,设,且,则的值是( )
A.0.294 B.0.42 C.0.5 D.0.6
3.根据分类变量和的样本观察数据的计算结果,有不少于的把握认为和有关,则的一个可能取值为( )
0.10 0.05 0.025 0.010 0.005
2.706 3.841 5.024 6.635 7.879
A.3.971 B.5.872 C.6.775 D.9.698
4.已知空间向量,若,则( )
A.5 B. C. D.
5.若为函数的极大值点,则( )
A. B. C. D.
6.对于集合和常数,定义:为集合相对的“正切方差”.若集合,则( )
A. B.1 C. D.2
7.若,则的大小关系为( )
A. B.
C. D.
8.某人在次射击中击中目标的次数为,且,记,,若是唯一的最大值,则的值为( )
A.7 B.7.7 C.8.4 D.9.1
二 多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,选对但不全的得2分,有选错的得0分)
9.下列结论正确的是( )
A.对于成对样本数据,样本相关系数越大,相关性越强
B.利用进行独立性检验时,的值越大,说明有更大把握认为两事件有关系
C.线性回归直线方程至少经过样本点数据中的一个点
D.用模型拟合一组数据时,设,得到回归方程,则
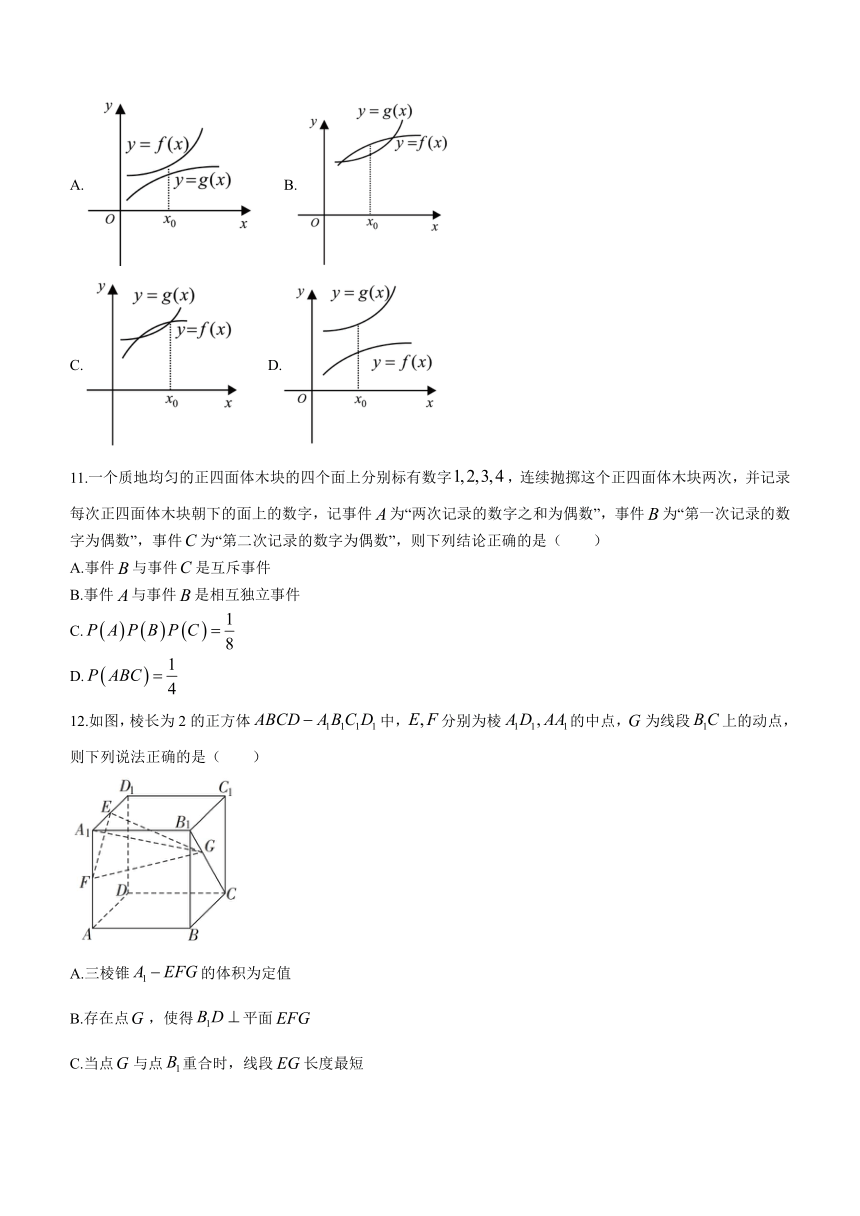
10.已知函数的导函数图象如图,那么的图象可能是( )
A. B.
C. D.
11.一个质地均匀的正四面体木块的四个面上分别标有数字,连续抛掷这个正四面体木块两次,并记录每次正四面体木块朝下的面上的数字,记事件为“两次记录的数字之和为偶数”,事件为“第一次记录的数字为偶数”,事件为“第二次记录的数字为偶数”,则下列结论正确的是( )
A.事件与事件是互斥事件
B.事件与事件是相互独立事件
C.
D.
12.如图,棱长为2的正方体中,分别为棱的中点,为线段上的动点,则下列说法正确的是( )
A.三棱锥的体积为定值
B.存在点,使得平面
C.当点与点重合时,线段长度最短
D.设直线与平面所成角为,则的最小值为
三 填空题(本大题共4小题,每小题5分,共20分)
13.已知随机变量,且,则__________.
14.甲 乙 丙三人相互做传球训练,第1次由甲将球传出,每次传球时,传球者都等可能地将球传给另外两个人中的任何一人,则4次传球后球在甲手中的概率为__________.
15.已知函数的导函数为,若,且,则不等式的解集为__________.
16.古代城池中的“瓮城”,又叫“曲池”,是加装在城门前面或里面的又一层门,若敌人攻入瓮城中,可形成“翁中捉鳖”之势.如下图的“曲池”是上 下底面均为半圆形的柱体,平面为的中点,则直线与平面所成角的正弦值为__________.
四 解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)
已知平行六面体,底面是正方形,,,设.
(1)试用表示;
(2)求线段的长度.
18.(本小题满分12分)
某有限公司通过技术革新和能力提升,每月售出的产品数量不断增加,下表为该公司今年月份售出的产品数量.
月份 1 2 3 4
售出的产品数量万件 6.1 6.3 6.7 6.9
(1)试根据样本相关系数的值判断售出的产品数量(万件)与月份线性相关性强弱(若,则认为变量和变量高度线性相关)(结果保留两位小数);
(2)求关于的线性回归方程,并预测该公司5月份售出的产品数量.
参考公式:.
19.(本小题满分12分)
已知函数.
(1)若曲线在点处的切线与曲线在点处的切线平行,求实数的值;
(2)若函数的图象与的图象有两个公共点,求实数的取值范围.
20.(本小题满分12分)
如图所示的几何体中,平面平面为等腰直角三角形,,四边形为直角梯形,.
(1)求证:平面;
(2)线段上是否存在点满足,使得平面?若存在,求出的值;若不存在,说明理由.
21.(本小题满分12分)
某学校组织“中亚峰会”知识竞赛,有两类问题,每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答.若回答错误,则该同学比赛结束;若回答正确,则从另一类问题中再随机抽取一个问题回答,无论回答正确与否,该同学比赛结束.类问题中的每个问题回答正确得分,否则得0分;类问题中的每个问题回答正确得分,否则得0分.已知学生甲能正确回答类问题的概率为,能正确回答类问题的概率为,且能正确回答问题的概率与回答次序无关.
(1)若学生甲先回答类问题,,记为学生甲的累计得分,求的分布列和数学期望.
(2)若,则学生甲应选择先回答哪类问题,使得累计得分的数学期望最大?并说明理由.
22.(本小题满分12分)
已知函数.
(1)若函数在区间上单调递增,求实数的取值范围;
(2)求证:当时,.
漳州市2022-2023学年高二下学期期末教学质量检测
数学参考答案
评分说明:
1.本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制定相应的评分细则.
2.对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应给分数的一半;如果后继部分的解答有较严重的错误,就不再给分.
3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.
4.只给整数分数.选择题和填空题不给中间分.
一 单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的
1.B 2.D 3.D 4.C 5.B 6.C 7.A 8.A
二 多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,选对但不全的得2分,有选错的得0分)
9.BD 10.BD 11.BCD 12.ABD
三 填空题(本大题共4小题,每小题5分,共20分)
13.0.2 14. 15. 16.
四 解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)
解:(1)
(2),
,
,
.
18.(本小题满分12分)
解:(1)
,
,
售出的产品数量(万件)与月份具有高度线性相关.
(2),
,
,
当,可得万件,
预测该公司5月份出售产品数量为7.2万件.
19.(本小题满分12分)
解:(1)
依题意得,即,解得.
故,
在点处的切线方程为,即;
而在点处的切线方程为,这两条切线平行,故.
(2)函数的图象与的图象有两个公共点
方程有两个不等实根
方程有两个不等实根
方程有两个不等实根
直线与函数的图象有两个交点
当时,单调递增;当时,单调递减.
有极大值,也是最大值为.
当时,;当时,
可以画出的草图:(如上图)
由图可知当时,直线与函数的图象有两个交点,
即函数的图象与的图象有两个公共点,故.
20.(本小题满分12分)
解:(1)四边形是平行四边形.
平面平面平面
(2)取的中点为
平面平面平面,平面平面
平面
以点为坐标原点,分别以直线为轴,轴建立空间直角坐标系,则轴在平面内.
,
,,
.
设平面的法向量为
即
令,则.
,
.
又平面的法向量为平面,
所以.
.
所以在线段上存在点,使平面,且的值是
21.(本小题满分12分)
解:(1)由题知,
,
的分布列为:
0 20 100
0.2 0.32 0.48
(2)学生甲选择先回答类问题时:
,
学生甲选择先回答类问题时:
,
.
学生甲应选择先回答类问题.
22.(本小题满分12分)
解:的定义域为.
(1)依题意得:对恒成立
对恒成立
令,
则,
当时,,
故在上单调递增,
所以的最小值为.
故,即的取值范围为.
(2)(法一)当时,
由得在上
单调递增,
又,
由零点存在定理可得在上有唯一零点,
设此零点为,则,有,
两边取对数并整理得,
当时,单调递减;
当时,单调递增,
故
.
即当时,.
(法二)我们先证明,,
当且仅当时等号成立.
构造函数,则,
当时,单调递减;
当时,单调递增,
故,当且仅当时等号成立.
当时,对两边同时取对数有,
故当时,当且仅当时等号成立.
所以,
两个“”中等号成立的条件分别为和,
故当时,.
当时,,又,
所以;
当时,,又.
综上所述,当时,.
数学试题
(考试时间:120分钟满分:150分)
考生注意:
1.答题前,考生务必在试题卷 答题卡规定的地方填写自己的准考证号 姓名.考生要认真核对答题卡上粘贴的条形码的“准考证号 姓名”与考生本人准考证号 姓名是否一致.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.
3.考试结束,考生必须将试题卷和答题卡一并交回.
一 单项选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列导数运算正确的是( )
A. B.
C. D.
2.已知事件,设,且,则的值是( )
A.0.294 B.0.42 C.0.5 D.0.6
3.根据分类变量和的样本观察数据的计算结果,有不少于的把握认为和有关,则的一个可能取值为( )
0.10 0.05 0.025 0.010 0.005
2.706 3.841 5.024 6.635 7.879
A.3.971 B.5.872 C.6.775 D.9.698
4.已知空间向量,若,则( )
A.5 B. C. D.
5.若为函数的极大值点,则( )
A. B. C. D.
6.对于集合和常数,定义:为集合相对的“正切方差”.若集合,则( )
A. B.1 C. D.2
7.若,则的大小关系为( )
A. B.
C. D.
8.某人在次射击中击中目标的次数为,且,记,,若是唯一的最大值,则的值为( )
A.7 B.7.7 C.8.4 D.9.1
二 多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,选对但不全的得2分,有选错的得0分)
9.下列结论正确的是( )
A.对于成对样本数据,样本相关系数越大,相关性越强
B.利用进行独立性检验时,的值越大,说明有更大把握认为两事件有关系
C.线性回归直线方程至少经过样本点数据中的一个点
D.用模型拟合一组数据时,设,得到回归方程,则
10.已知函数的导函数图象如图,那么的图象可能是( )
A. B.
C. D.
11.一个质地均匀的正四面体木块的四个面上分别标有数字,连续抛掷这个正四面体木块两次,并记录每次正四面体木块朝下的面上的数字,记事件为“两次记录的数字之和为偶数”,事件为“第一次记录的数字为偶数”,事件为“第二次记录的数字为偶数”,则下列结论正确的是( )
A.事件与事件是互斥事件
B.事件与事件是相互独立事件
C.
D.
12.如图,棱长为2的正方体中,分别为棱的中点,为线段上的动点,则下列说法正确的是( )
A.三棱锥的体积为定值
B.存在点,使得平面
C.当点与点重合时,线段长度最短
D.设直线与平面所成角为,则的最小值为
三 填空题(本大题共4小题,每小题5分,共20分)
13.已知随机变量,且,则__________.
14.甲 乙 丙三人相互做传球训练,第1次由甲将球传出,每次传球时,传球者都等可能地将球传给另外两个人中的任何一人,则4次传球后球在甲手中的概率为__________.
15.已知函数的导函数为,若,且,则不等式的解集为__________.
16.古代城池中的“瓮城”,又叫“曲池”,是加装在城门前面或里面的又一层门,若敌人攻入瓮城中,可形成“翁中捉鳖”之势.如下图的“曲池”是上 下底面均为半圆形的柱体,平面为的中点,则直线与平面所成角的正弦值为__________.
四 解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)
已知平行六面体,底面是正方形,,,设.
(1)试用表示;
(2)求线段的长度.
18.(本小题满分12分)
某有限公司通过技术革新和能力提升,每月售出的产品数量不断增加,下表为该公司今年月份售出的产品数量.
月份 1 2 3 4
售出的产品数量万件 6.1 6.3 6.7 6.9
(1)试根据样本相关系数的值判断售出的产品数量(万件)与月份线性相关性强弱(若,则认为变量和变量高度线性相关)(结果保留两位小数);
(2)求关于的线性回归方程,并预测该公司5月份售出的产品数量.
参考公式:.
19.(本小题满分12分)
已知函数.
(1)若曲线在点处的切线与曲线在点处的切线平行,求实数的值;
(2)若函数的图象与的图象有两个公共点,求实数的取值范围.
20.(本小题满分12分)
如图所示的几何体中,平面平面为等腰直角三角形,,四边形为直角梯形,.
(1)求证:平面;
(2)线段上是否存在点满足,使得平面?若存在,求出的值;若不存在,说明理由.
21.(本小题满分12分)
某学校组织“中亚峰会”知识竞赛,有两类问题,每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答.若回答错误,则该同学比赛结束;若回答正确,则从另一类问题中再随机抽取一个问题回答,无论回答正确与否,该同学比赛结束.类问题中的每个问题回答正确得分,否则得0分;类问题中的每个问题回答正确得分,否则得0分.已知学生甲能正确回答类问题的概率为,能正确回答类问题的概率为,且能正确回答问题的概率与回答次序无关.
(1)若学生甲先回答类问题,,记为学生甲的累计得分,求的分布列和数学期望.
(2)若,则学生甲应选择先回答哪类问题,使得累计得分的数学期望最大?并说明理由.
22.(本小题满分12分)
已知函数.
(1)若函数在区间上单调递增,求实数的取值范围;
(2)求证:当时,.
漳州市2022-2023学年高二下学期期末教学质量检测
数学参考答案
评分说明:
1.本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制定相应的评分细则.
2.对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应给分数的一半;如果后继部分的解答有较严重的错误,就不再给分.
3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.
4.只给整数分数.选择题和填空题不给中间分.
一 单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的
1.B 2.D 3.D 4.C 5.B 6.C 7.A 8.A
二 多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,选对但不全的得2分,有选错的得0分)
9.BD 10.BD 11.BCD 12.ABD
三 填空题(本大题共4小题,每小题5分,共20分)
13.0.2 14. 15. 16.
四 解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)
解:(1)
(2),
,
,
.
18.(本小题满分12分)
解:(1)
,
,
售出的产品数量(万件)与月份具有高度线性相关.
(2),
,
,
当,可得万件,
预测该公司5月份出售产品数量为7.2万件.
19.(本小题满分12分)
解:(1)
依题意得,即,解得.
故,
在点处的切线方程为,即;
而在点处的切线方程为,这两条切线平行,故.
(2)函数的图象与的图象有两个公共点
方程有两个不等实根
方程有两个不等实根
方程有两个不等实根
直线与函数的图象有两个交点
当时,单调递增;当时,单调递减.
有极大值,也是最大值为.
当时,;当时,
可以画出的草图:(如上图)
由图可知当时,直线与函数的图象有两个交点,
即函数的图象与的图象有两个公共点,故.
20.(本小题满分12分)
解:(1)四边形是平行四边形.
平面平面平面
(2)取的中点为
平面平面平面,平面平面
平面
以点为坐标原点,分别以直线为轴,轴建立空间直角坐标系,则轴在平面内.
,
,,
.
设平面的法向量为
即
令,则.
,
.
又平面的法向量为平面,
所以.
.
所以在线段上存在点,使平面,且的值是
21.(本小题满分12分)
解:(1)由题知,
,
的分布列为:
0 20 100
0.2 0.32 0.48
(2)学生甲选择先回答类问题时:
,
学生甲选择先回答类问题时:
,
.
学生甲应选择先回答类问题.
22.(本小题满分12分)
解:的定义域为.
(1)依题意得:对恒成立
对恒成立
令,
则,
当时,,
故在上单调递增,
所以的最小值为.
故,即的取值范围为.
(2)(法一)当时,
由得在上
单调递增,
又,
由零点存在定理可得在上有唯一零点,
设此零点为,则,有,
两边取对数并整理得,
当时,单调递减;
当时,单调递增,
故
.
即当时,.
(法二)我们先证明,,
当且仅当时等号成立.
构造函数,则,
当时,单调递减;
当时,单调递增,
故,当且仅当时等号成立.
当时,对两边同时取对数有,
故当时,当且仅当时等号成立.
所以,
两个“”中等号成立的条件分别为和,
故当时,.
当时,,又,
所以;
当时,,又.
综上所述,当时,.
同课章节目录
