3.2.1函数的最值第一课时-高一数学必修一课件(共16张PPT)
文档属性
| 名称 | 3.2.1函数的最值第一课时-高一数学必修一课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-11 06:11:30 | ||
图片预览





文档简介
(共16张PPT)
3.2.1 函数的单调性——最值
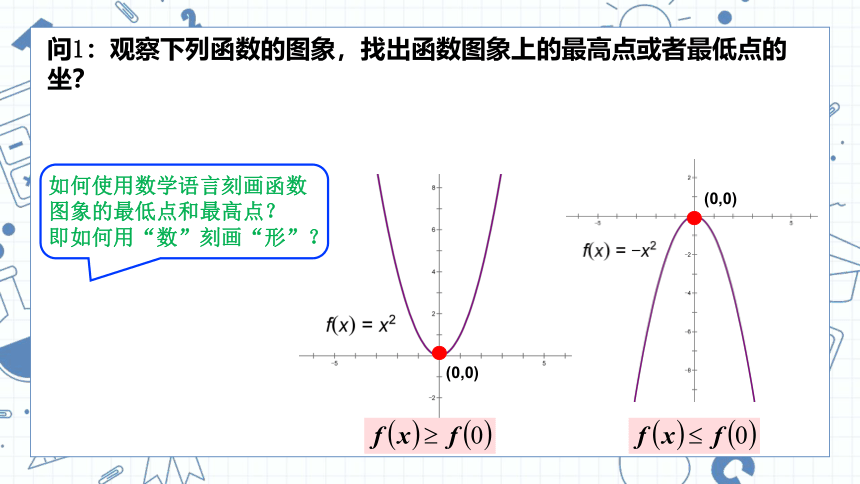
问1:观察下列函数的图象,找出函数图象上的最高点或者最低点的坐?
如何使用数学语言刻画函数图象的最低点和最高点?
即如何用“数”刻画“形”?
(0,0)
(0,0)
函数 最大值 最小值
条件 设函数y=f(x)的定义域为I,若存在实数M满足:
x∈I,都有f(x)≤M; x0∈I,使得f(x0)=M. x∈I,都有f(x)≥M;
x0∈I,使得f(x0)=M.
结论 称M是函数y=f(x)的最大值 称M是函数y=f(x)的最小值
几何意义 f(x)图象上最高点的纵坐标 f(x)图象上最低点的纵坐标
①最大(小)值必须是一个确定的函数值,且为值域中的一个元素.
无最小值
②求函数的最值应先判断单调性(图象/定义/运算性质).
任意性
存在性
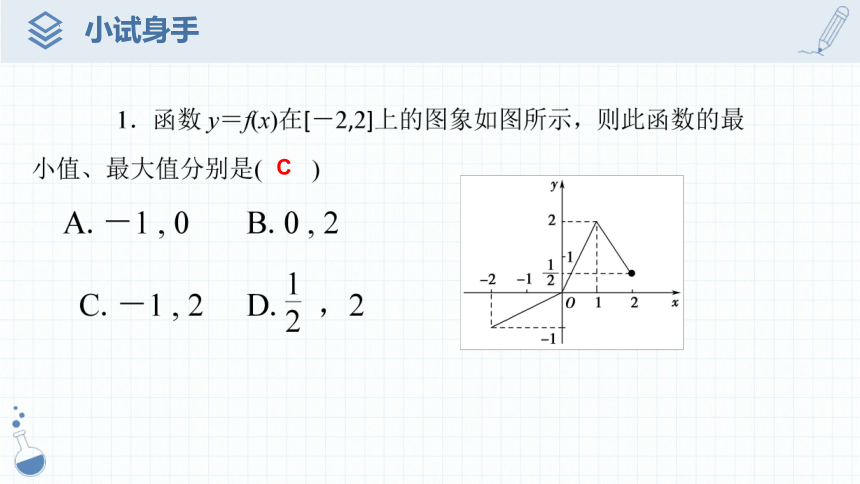
C
(1)若函数y=f(x)在区间[a,b]上单调递增,则f(x)的最大值为f(b),最小值为f(a).
(2)若函数y=f(x)在区间[a,b]上单调递减,则f(x)的最大值为f(a),最小值为f(b).
(3)若函数y=f(x)有多个单调区间,那就先求出各区间上的最值,再从各区间的最值中决定出最大(小)值.函数的最大(小)值是整个值域范围内的最大(小)值.
(4)如果函数定义域为区间,则不但要考虑函数在该区间上的单调性,还要考虑端点处的函数值或者发展趋势.
函数的最值与单调性
例4.“菊花”烟花是最壮观的烟花之一.制造时一般是期望它在达到最高点时爆裂.如果烟花距地面的高度h(单位:m) 与时间t(单位:s)之间的关系为 h(t)=-4.9t2+14.7t+18 ,那么烟花冲出后什么时刻爆裂是最佳时刻?这时离地面的高度是多少(精确到1 m)?
分析:烟花的高度是时间的二次函数,根据题意就是求出这个二次函数在什么时刻达到最大值,以及这个最大值是多少.
解:画出函数h(t)=-4.9t2+14.7t+18的图象.
函数图象的顶点就是烟花上升的最高点,顶点的横坐标就是烟花爆裂的最佳时刻,纵坐标就是这时距地面的高度.
由二次函数的知识可知,对于h(t)=-4.9t2+14.7t+18有:
∴烟花冲出后1.5秒是它爆裂的最佳时刻,这时距地面的高度为29 m.
例5.已知函数 ,求这个函数的最大值和最小值。
解:设x1,x2是区间[2,6]上的任意两个实数,且x1所以,函数 是区间[2,6]上单调递减.
对勾函数
例2:求下列函数的最值
(1)f(x)=x2-2x (2)f(x)=x2-2x(x∈[-1,2] ) (3)f(x)=x2-2x(x∈[0,3] ) (4)f(x)=x2-2x(x∈[-2,0] )
求二次函数在区间D上的最值:
由零点/开口/对称轴画图,最值在顶点或区间端点取得
(1)解决这类问题,要画出函数的图象,根据给定的区间截取符合要求的部分,根据图象写出最大值和最小值.
(2)常用结论:当二次函数图象开口向上时,自变量距离对称轴越远,对应的函数值越大;当图象开口向下时,则相反.
定轴定区间的二次函数的最值问题
【例2.1】求函数f(x)=x2-ax+1在区间[0,1]上的最小值。
求对称轴
以区间端
点为界移
对称轴
讨论对称轴+单调
性+最值
汇总结论
轴动区间定
求对称轴----分类讨论(移对称轴)①对称轴的范围,②讨论单调性;③求最值。下结论
【例2.1】求函数f(x)=x2-ax+1在区间[0,1]上的最大值。
求对称轴
以区间端
点为界移
对称轴
讨论对称轴+单调
性+最值
汇总结论
轴动区间定
求对称轴----分类讨论(移对称轴)①对称轴的范围,②讨论单调性;③求最值。下结论
[例2.2]函数f(x)=x2-x+1,x∈[t,t+1], t∈R, 求f(x)的最小值g(t).
求对称轴
以对称轴
为参照移
区间
讨论区间端点+单调
性+最值
汇总结论
轴定区间动
【轴定区间动】
1.求对称轴,画函数草图;
2.分类讨论(以对称轴为参照移区间):
区间端点的范围+讨论单调性+求最值;
3.下结论
【轴动区间定】
1.求对称轴;画函数草图;
2.分类讨论(以区间端点为界移对称轴):
对称轴的范围+讨论单调性+求最值;
3.下结论
最值 条件(I是函数f(x)的定义域) 几何意义
最大值 ①对于任意x∈I,都有f(x)≤M ②存在x0∈I,使得f(x0)=M 函数y=f(x)图象上
最高点的纵坐标
最小值 ①对于任意x∈I,都有f(x)≥M ②存在x0∈I,使得f(x0)=M 函数y=f(x)图象上
最低点的纵坐标
函数最大(小)值的定义
常用的求函数最值的方法
(1)利用函数图像判断最值.
(2)利用函数的单调性判断最值.
阶段小结:求函数最值or值域的方法
注意新元范围
3.2.1 函数的单调性——最值
问1:观察下列函数的图象,找出函数图象上的最高点或者最低点的坐?
如何使用数学语言刻画函数图象的最低点和最高点?
即如何用“数”刻画“形”?
(0,0)
(0,0)
函数 最大值 最小值
条件 设函数y=f(x)的定义域为I,若存在实数M满足:
x∈I,都有f(x)≤M; x0∈I,使得f(x0)=M. x∈I,都有f(x)≥M;
x0∈I,使得f(x0)=M.
结论 称M是函数y=f(x)的最大值 称M是函数y=f(x)的最小值
几何意义 f(x)图象上最高点的纵坐标 f(x)图象上最低点的纵坐标
①最大(小)值必须是一个确定的函数值,且为值域中的一个元素.
无最小值
②求函数的最值应先判断单调性(图象/定义/运算性质).
任意性
存在性
C
(1)若函数y=f(x)在区间[a,b]上单调递增,则f(x)的最大值为f(b),最小值为f(a).
(2)若函数y=f(x)在区间[a,b]上单调递减,则f(x)的最大值为f(a),最小值为f(b).
(3)若函数y=f(x)有多个单调区间,那就先求出各区间上的最值,再从各区间的最值中决定出最大(小)值.函数的最大(小)值是整个值域范围内的最大(小)值.
(4)如果函数定义域为区间,则不但要考虑函数在该区间上的单调性,还要考虑端点处的函数值或者发展趋势.
函数的最值与单调性
例4.“菊花”烟花是最壮观的烟花之一.制造时一般是期望它在达到最高点时爆裂.如果烟花距地面的高度h(单位:m) 与时间t(单位:s)之间的关系为 h(t)=-4.9t2+14.7t+18 ,那么烟花冲出后什么时刻爆裂是最佳时刻?这时离地面的高度是多少(精确到1 m)?
分析:烟花的高度是时间的二次函数,根据题意就是求出这个二次函数在什么时刻达到最大值,以及这个最大值是多少.
解:画出函数h(t)=-4.9t2+14.7t+18的图象.
函数图象的顶点就是烟花上升的最高点,顶点的横坐标就是烟花爆裂的最佳时刻,纵坐标就是这时距地面的高度.
由二次函数的知识可知,对于h(t)=-4.9t2+14.7t+18有:
∴烟花冲出后1.5秒是它爆裂的最佳时刻,这时距地面的高度为29 m.
例5.已知函数 ,求这个函数的最大值和最小值。
解:设x1,x2是区间[2,6]上的任意两个实数,且x1
对勾函数
例2:求下列函数的最值
(1)f(x)=x2-2x (2)f(x)=x2-2x(x∈[-1,2] ) (3)f(x)=x2-2x(x∈[0,3] ) (4)f(x)=x2-2x(x∈[-2,0] )
求二次函数在区间D上的最值:
由零点/开口/对称轴画图,最值在顶点或区间端点取得
(1)解决这类问题,要画出函数的图象,根据给定的区间截取符合要求的部分,根据图象写出最大值和最小值.
(2)常用结论:当二次函数图象开口向上时,自变量距离对称轴越远,对应的函数值越大;当图象开口向下时,则相反.
定轴定区间的二次函数的最值问题
【例2.1】求函数f(x)=x2-ax+1在区间[0,1]上的最小值。
求对称轴
以区间端
点为界移
对称轴
讨论对称轴+单调
性+最值
汇总结论
轴动区间定
求对称轴----分类讨论(移对称轴)①对称轴的范围,②讨论单调性;③求最值。下结论
【例2.1】求函数f(x)=x2-ax+1在区间[0,1]上的最大值。
求对称轴
以区间端
点为界移
对称轴
讨论对称轴+单调
性+最值
汇总结论
轴动区间定
求对称轴----分类讨论(移对称轴)①对称轴的范围,②讨论单调性;③求最值。下结论
[例2.2]函数f(x)=x2-x+1,x∈[t,t+1], t∈R, 求f(x)的最小值g(t).
求对称轴
以对称轴
为参照移
区间
讨论区间端点+单调
性+最值
汇总结论
轴定区间动
【轴定区间动】
1.求对称轴,画函数草图;
2.分类讨论(以对称轴为参照移区间):
区间端点的范围+讨论单调性+求最值;
3.下结论
【轴动区间定】
1.求对称轴;画函数草图;
2.分类讨论(以区间端点为界移对称轴):
对称轴的范围+讨论单调性+求最值;
3.下结论
最值 条件(I是函数f(x)的定义域) 几何意义
最大值 ①对于任意x∈I,都有f(x)≤M ②存在x0∈I,使得f(x0)=M 函数y=f(x)图象上
最高点的纵坐标
最小值 ①对于任意x∈I,都有f(x)≥M ②存在x0∈I,使得f(x0)=M 函数y=f(x)图象上
最低点的纵坐标
函数最大(小)值的定义
常用的求函数最值的方法
(1)利用函数图像判断最值.
(2)利用函数的单调性判断最值.
阶段小结:求函数最值or值域的方法
注意新元范围
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
