3.1.1函数的概念第二课时定义域值域-高一必修一同步课件(共23张PPT)
文档属性
| 名称 | 3.1.1函数的概念第二课时定义域值域-高一必修一同步课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-11 06:16:32 | ||
图片预览








文档简介
(共23张PPT)
3.1.1函数的概念
第二课时
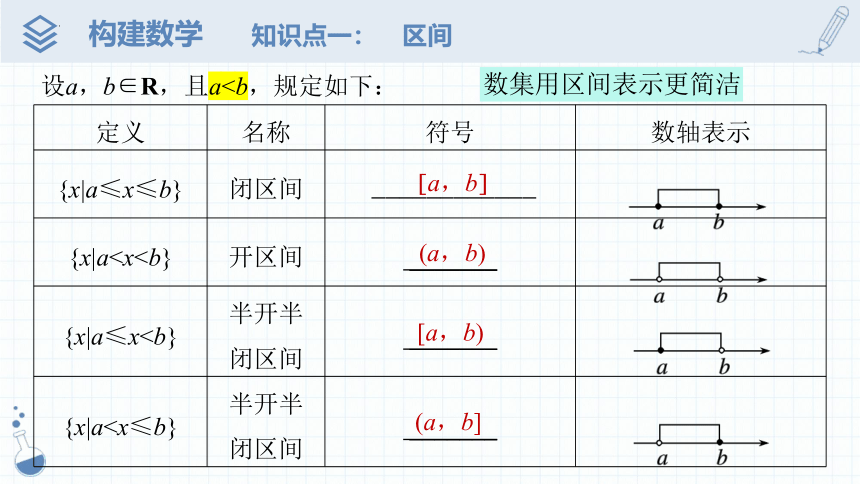
知识点一: 区间
设a,b∈R,且a定义 名称 符号 数轴表示
{x|a≤x≤b} 闭区间 ____________
{x|a{x|a≤x{x|a[a,b]
(a,b)
[a,b)
(a,b]
{x|x≥a} [a,+∞)
{x|x>a} (a,+∞)
{x|x≤a} (-∞,a]
{x|xR (-∞,+∞)
知识点一 区间
例1 把下列数集用区间表示:
(1){x|x≥-1};(2){x|x<0};(3){x|-1解 (1){x|x≥-1}=[-1,+∞); (2){x|x<0}=(-∞,0);
(3){x|-1跟踪训练1 (1)集合{x|-2 (-2,0)∪(0,2]
(2)已知区间(a2+a+1,7],则实数a的取值范围是________.
(-3,2)
问1:是不是任何数集都能用区间表示?
问2:“∞”是数吗?如何正确使用“∞”?
析:“∞”读作“无穷大”,是一个符号,使用时必须加上“+,-”符号不是数.
以“-∞”或“+∞”作为区间一端时,这一端必须是小括号.
析:如集合{0}就不能用区间表示,区间主要针对不等式使用更简洁
函数应用——1、利用函数解析式求函数值
函数的定义域通常由问题的实际背景确定,给出函数解析式,若没有指明定义域,则函数的定义域是指能使这个式子有意义的实数的集合.
“由里往外”逐层求值.
33
16
分段函数破解攻略:
先找到自变量所对应那段的函数解析式
函数应用——1、利用函数解析式求函数值
函数的应用2、求函数的定义域(具体函数)
(-∞,4)∪(4,+∞)
{x|x≠0且x≠-2}
若已给出函数解析式但无指明其定义域,
则定义域默认为使解析式有意义的实数的集合。
(-∞,1)∪(1,2)∪(2,+∞)
(-∞,1)∪(1,4]
(-∞,-2)∪(-2,0)∪(0,+∞)
函数的定义域通常也由问题的实际背景确定。
如果只给出解析式,而没有指明它的定义域,那么函数的定义域就是指能使这个式子有意义的实数的集合。
①负数不能开平方(负数不能开偶次方);
②分母不能为零;
③有限个函数的四则运算得到的新函数,它的定
义域是这有限个函数定义域的交集.
思考1:下列函数中哪个与函数y=x相等( )
A. B.
C. D.
B
如果两个函数定义域相同,并且对应关系完全一致,我们就称这两个函数相等(或为同一函数)
关注函数的三要素
思考2:如何判断两个函数是否为同一函数
函数应用——3、判断相等函数
若两个函数的定义域和对应关系相同,则它们为同一个函数.
(两个函数相等)
(与字母无关)
对应关系相同,定义域不同
思考3:定义域和值域都相同的两个函数是否一定相等?
如:“y=x+1”与“y=2x”的定义域、值域均为R,但对应关系不同.
对应关系相同,定义域不同
[2,+∞)
(-∞,-2]∪[2,+∞)
R
{x|x≠0}
函数应用——3、判断相等函数
函数应用4:求函数值域的方法
1.基本函数图像观察法
1.基本函数图像法
渐进线
函数应用4:求函数值域的方法
1.基本函数--配方法(二次函数型)
函数应用4:求函数值域的方法
1.复杂函数图像变换观察法
函数应用4:求函数值域的方法
2.换元法
函数应用4:求函数值域的方法
注意新元的范围
2.换元法
函数应用4:求函数值域的方法
3.分离常数法
1.适用于分子分母均含变量的分式
2.分离目的:化为熟悉结构,便于利用反比例函数或基本不等式求
分式的范围、最值等
把分子中的变量分离掉,使分子化为常数
3.分离方法:分子配凑出与分母一样的结构→约分
函数应用4:求函数值域的方法
3.分离常数法
把分子中的变量分离掉,使分子化为常数
函数应用4:求函数值域的方法
回顾本节课你有什么收获?
函数
定义
核心概念
判断同一函数的方法
三要素
a∈[0,4]
t+1∈[0,4]
t∈[-1,3]
①同一题目中,同一对应关系f作用的整个对象的取值范围相同.
a-2∈[0,4]
②任何函数的定义域均指自变量的取值范围.
引例中, f(x)的定义域是指x的范围;
f(x+1)的定义域是指x的范围.
f(a-2)的定义域是指a的范围.
只是用同一字母来表示两个函数的自变量,范围可能不同.
两个“x”不同
x∈[-1,3]
a∈[2,6]
x+1∈[0,4]
f作用对象的范围:
函数的定义域:
函数应用5:求抽象函数定义域的方法
考点四:求函数的定义域(抽象函数)
f(x) f(x+1)
定义域 (自变量的范围)
同一f作用对象的范围
0≤x≤1
0≤x≤1
0≤x+1≤1
﹣1≤x≤0
[-1,0]
[例]解:∵f(x)的定义域为[0,1],
即0≤x≤1;
∴对于f(x+1)有0≤x+1≤1,
解得-1≤x≤0.
∴f(x+1)的定义域为[-1,0]
[变式4]已知f(x)的定义域为[-2,4],则g(x)=f(x)+f(-x)的定义域是___.
2
[2,3]
[-2,-1]
+
[-2,-1)
[-2,2]
Key:同一f作用对象的范围
3.1.1函数的概念
第二课时
知识点一: 区间
设a,b∈R,且a
{x|a≤x≤b} 闭区间 ____________
{x|a
(a,b)
[a,b)
(a,b]
{x|x≥a} [a,+∞)
{x|x>a} (a,+∞)
{x|x≤a} (-∞,a]
{x|x
知识点一 区间
例1 把下列数集用区间表示:
(1){x|x≥-1};(2){x|x<0};(3){x|-1
(3){x|-1
(2)已知区间(a2+a+1,7],则实数a的取值范围是________.
(-3,2)
问1:是不是任何数集都能用区间表示?
问2:“∞”是数吗?如何正确使用“∞”?
析:“∞”读作“无穷大”,是一个符号,使用时必须加上“+,-”符号不是数.
以“-∞”或“+∞”作为区间一端时,这一端必须是小括号.
析:如集合{0}就不能用区间表示,区间主要针对不等式使用更简洁
函数应用——1、利用函数解析式求函数值
函数的定义域通常由问题的实际背景确定,给出函数解析式,若没有指明定义域,则函数的定义域是指能使这个式子有意义的实数的集合.
“由里往外”逐层求值.
33
16
分段函数破解攻略:
先找到自变量所对应那段的函数解析式
函数应用——1、利用函数解析式求函数值
函数的应用2、求函数的定义域(具体函数)
(-∞,4)∪(4,+∞)
{x|x≠0且x≠-2}
若已给出函数解析式但无指明其定义域,
则定义域默认为使解析式有意义的实数的集合。
(-∞,1)∪(1,2)∪(2,+∞)
(-∞,1)∪(1,4]
(-∞,-2)∪(-2,0)∪(0,+∞)
函数的定义域通常也由问题的实际背景确定。
如果只给出解析式,而没有指明它的定义域,那么函数的定义域就是指能使这个式子有意义的实数的集合。
①负数不能开平方(负数不能开偶次方);
②分母不能为零;
③有限个函数的四则运算得到的新函数,它的定
义域是这有限个函数定义域的交集.
思考1:下列函数中哪个与函数y=x相等( )
A. B.
C. D.
B
如果两个函数定义域相同,并且对应关系完全一致,我们就称这两个函数相等(或为同一函数)
关注函数的三要素
思考2:如何判断两个函数是否为同一函数
函数应用——3、判断相等函数
若两个函数的定义域和对应关系相同,则它们为同一个函数.
(两个函数相等)
(与字母无关)
对应关系相同,定义域不同
思考3:定义域和值域都相同的两个函数是否一定相等?
如:“y=x+1”与“y=2x”的定义域、值域均为R,但对应关系不同.
对应关系相同,定义域不同
[2,+∞)
(-∞,-2]∪[2,+∞)
R
{x|x≠0}
函数应用——3、判断相等函数
函数应用4:求函数值域的方法
1.基本函数图像观察法
1.基本函数图像法
渐进线
函数应用4:求函数值域的方法
1.基本函数--配方法(二次函数型)
函数应用4:求函数值域的方法
1.复杂函数图像变换观察法
函数应用4:求函数值域的方法
2.换元法
函数应用4:求函数值域的方法
注意新元的范围
2.换元法
函数应用4:求函数值域的方法
3.分离常数法
1.适用于分子分母均含变量的分式
2.分离目的:化为熟悉结构,便于利用反比例函数或基本不等式求
分式的范围、最值等
把分子中的变量分离掉,使分子化为常数
3.分离方法:分子配凑出与分母一样的结构→约分
函数应用4:求函数值域的方法
3.分离常数法
把分子中的变量分离掉,使分子化为常数
函数应用4:求函数值域的方法
回顾本节课你有什么收获?
函数
定义
核心概念
判断同一函数的方法
三要素
a∈[0,4]
t+1∈[0,4]
t∈[-1,3]
①同一题目中,同一对应关系f作用的整个对象的取值范围相同.
a-2∈[0,4]
②任何函数的定义域均指自变量的取值范围.
引例中, f(x)的定义域是指x的范围;
f(x+1)的定义域是指x的范围.
f(a-2)的定义域是指a的范围.
只是用同一字母来表示两个函数的自变量,范围可能不同.
两个“x”不同
x∈[-1,3]
a∈[2,6]
x+1∈[0,4]
f作用对象的范围:
函数的定义域:
函数应用5:求抽象函数定义域的方法
考点四:求函数的定义域(抽象函数)
f(x) f(x+1)
定义域 (自变量的范围)
同一f作用对象的范围
0≤x≤1
0≤x≤1
0≤x+1≤1
﹣1≤x≤0
[-1,0]
[例]解:∵f(x)的定义域为[0,1],
即0≤x≤1;
∴对于f(x+1)有0≤x+1≤1,
解得-1≤x≤0.
∴f(x+1)的定义域为[-1,0]
[变式4]已知f(x)的定义域为[-2,4],则g(x)=f(x)+f(-x)的定义域是___.
2
[2,3]
[-2,-1]
+
[-2,-1)
[-2,2]
Key:同一f作用对象的范围
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
