福建省晋江市五校2022-2023学年高二下学期期末联考数学试题(Word版含答案)
文档属性
| 名称 | 福建省晋江市五校2022-2023学年高二下学期期末联考数学试题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 782.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-11 00:00:00 | ||
图片预览




文档简介
晋江市五校2022-2023学年高二下学期期末联考数学科试卷
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.集合,,则( )
A. B. C. D.
2.复数的虚部为( )
A. B. C.2 D.
3.展开式中含项的系数为( )
A.15 B.30 C.60 D.120
4.甲、乙两校各有3名教师报名支教,其中甲校2男1女,乙校1男2女,若从甲校和乙校报名的教师中各任选1名,则选出的2名教师性别相同的概率是( )
A. B. C. D.
5.曲线在点处的切线的倾斜角为( )
A. B. C. D.
6.小华为了研究数学名次和物理名次的相关关系,记录了本班五名同学的数学和物理的名次,如图,后来发现第四名同学的数据记录有误,那么去掉数据后,下列说法错误的是( )
A.样本相关系数变大 B.残差平方和变大
C.变大 D.解释变量与响应变量的相关程度变强
7.若函数在处有极值10,则( )
A. B. C.6 D.15
8.已知函数,,分别与直线交于点A,B,则的最小值为( )
A. B. C. D.
二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9.设向量,,若,则的取值可能是( )
A. B.0 C.3 D.5
10.下列关于回归分析与独立性检验的说法正确的是( )
A.相关变量x,y的线性回归方程为,若样本点中心为,则
B.对于独立性检验,的值越大,说明两事件相关程度越大
C.回归分析是对两个变量确定性关系的分析,而独立性检验是分析两个变量之间的不确定性关系
D.在残差的散点图中,残差分布的水平带状区域的宽度越窄,其模型的拟合效果越好
11.关,则( )
A.
B.
C.
D.
12.已知A,B是两个事件,且,,则下列结论一定成立的是( ).
A.
B.若,则与独立
C.若与独立,且,则
D.若与独立,且,,则
三、填空题:本题共4小题,每小题5分,共20分.
13.若为奇函数,则______.
14.某学校开设了4门体育类选修课和4门艺术类选修课,学生需从这8门课中选修2门或3门课,并且每类选修课至少选修1门,则不同的选课方案共有______种(用数字作答).
15.某餐馆在A网站有200条评价,好评率为90%,在B网站有100条评价,好评率为87%.综合考虑这两个网站的信息,这家餐馆的好评率为______.
16.已知函数,则的最大值为______.
四、解答题:本题共6小题,共70分.解答应写出文字说明 证明过程或演算步骤.
17.已知函数,且.
(1)求的解析式;
(2)求曲线在处的切线方程.
18.某同学参加科普知识竞赛,需回答三个问题.竞赛规则规定:每题回答正确得100分,回答不正确得—100.假设这名同学每题回答正确的概率均为0.8,且各题回答正确与否相互之间没有影响.
(1)求这名同学回答这三个问题的总得分的概率分布和数学期望;
(2)求这名同学总得分不为负分(即)的概率.
19.一项试验旨在研究臭氧效应.实验方案如下:选40只小白鼠,随机地将其中20只分配到实验组,另外20只分配到对照组,实验组的小白鼠饲养在高浓度臭氧环境,对照组的小白鼠饲养在正常环境,一段时间后统计每只小白鼠体重的增加量(单位:g).实验结果如下:对照组的小白鼠体重的增加量从小到大排序为:
15.2 18.8 20.2 21.3 22.5 23.2 25.8 26.5 27.5 30.1
32.6 34.3 34.8 35.6 35.6 35.8 36.2 37.3 40.5 43.2
实验组的小白鼠体重的增加量从小到大排序为:
7.8 9.2 11.4 12.4 13.2 15.5 16.5 18.0 18.8 19.2
19.8 20.2 21.6 22.8 23.6 23.9 25.1 28.2 32.3 36.5
(1)设X表示指定的两只小白鼠中分配到对照组的只数,求X的分布列和数学期望;
(2)(i)求40只小鼠体重的增加量的中位数m,再分别统计两样本中小于m与不小于的数据的个数,完成如下列联表:
对照组
实验组
(ii)根据(i)中的列联表,依据小概率值的独立性检验,能否认为小白鼠在高浓度臭氧环境中与正常环境中体重的增加量有差异.
附:,其中.
0.100 0.050 0.010
2.706 3.841 6.635
20.为了切实加强学校体育工作,促进学生积极参加体育锻炼,养成良好的锻炼习惯,某高中学校计划优化课程,增加学生体育锻炼时间,提高体质健康水平,某体质监测中心抽取了该校10名学生进行体质测试,得到如下表格:
序号i 1 2 3 4 5 6 7 8 9 10
成绩(分) 38 41 44 51 54 56 58 64 74 80
记这10名学生体质测试成绩的平均分与方差分别为,,经计算,.
(1)求;
(2)经统计,高中生体质测试成绩近似服从正态分布,用,的值分别作为,的近似值,若监测中心计划从全市抽查100名高中生进行体质测试,记这100名高中生的体质测试成绩恰好落在区间的人数为,求的数学期望.
附:若,则,,.
21.已知函数,.
(1)讨论的单调性;
(2)当时,证明.
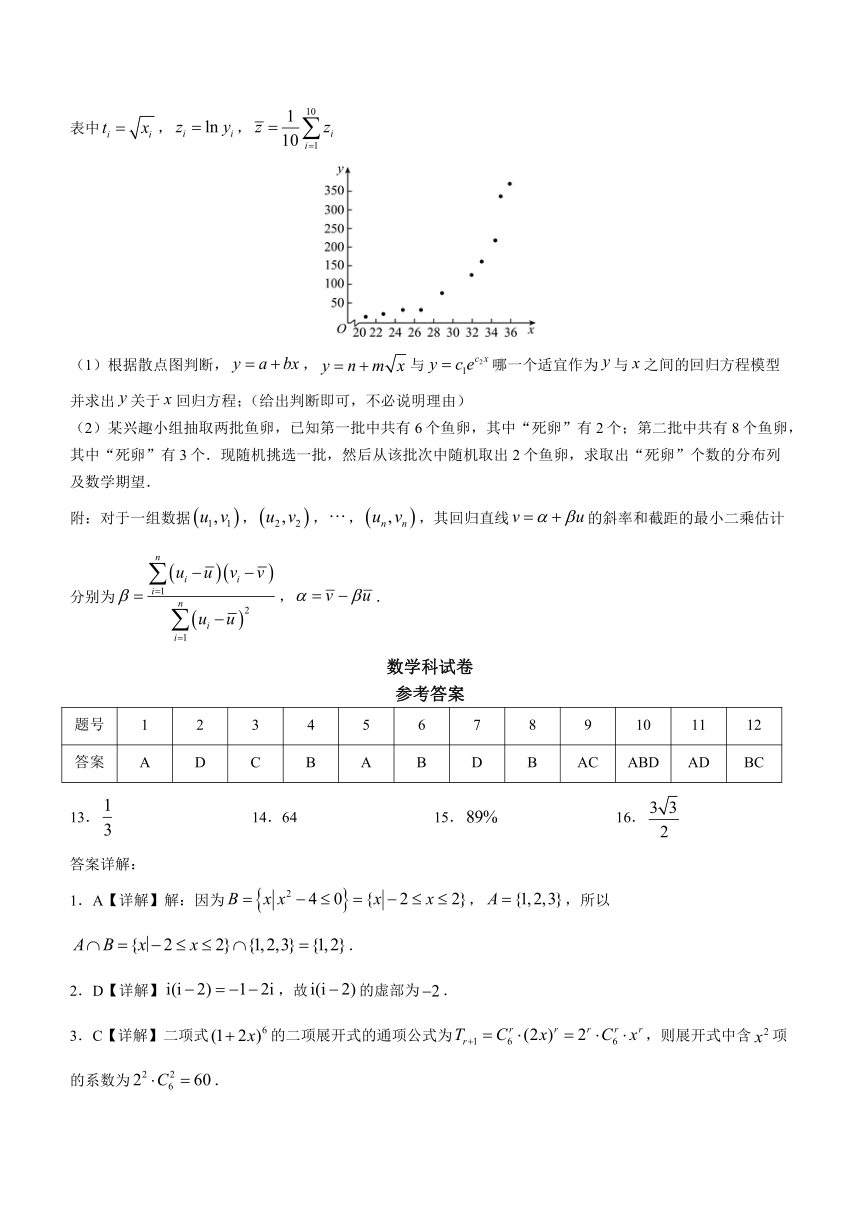
22.经观测,长江中某鱼类的产卵数与温度有关,现将收集到的温度和产卵数的10组观测数据作了初步处理,得到如图的散点图及一些统计量表.
360 54.5 1360 44 384
3 588 32 6430
表中,,
(1)根据散点图判断,,与哪一个适宜作为与之间的回归方程模型并求出关于回归方程;(给出判断即可,不必说明理由)
(2)某兴趣小组抽取两批鱼卵,已知第一批中共有6个鱼卵,其中“死卵”有2个;第二批中共有8个鱼卵,其中“死卵”有3个.现随机挑选一批,然后从该批次中随机取出2个鱼卵,求取出“死卵”个数的分布列及数学期望.
附:对于一组数据,,,,其回归直线的斜率和截距的最小二乘估计分别为,.
数学科试卷
参考答案
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 A D C B A B D B AC ABD AD BC
13. 14.64 15. 16.
答案详解:
1.A【详解】解:因为,,所以.
2.D【详解】,故的虚部为.
3.C【详解】二项式的二项展开式的通项公式为,则展开式中含项的系数为.
4.B【详解】
5.A【详解】由和切点可知,切线的斜率,即倾斜角,
6.B【详解】由散点图知,去掉后,与的线性相关程度变强,且为正相关,所以变大,变大,残差平方和变小.故ACD正确,B错误.
7.D【详解】由,得,由题意可知:,,得到,解得或,当,时,,所以不是极值点,当,时,,
所以在,上单调递增,在上单调递减,所以则在处取极小值10,符合题意.
所以,,所以.
8.B【详解】
由题意,,,其中,且,
所以,令,,
则时,解得,
所以时,;时,;
则在上单调递减,在上单调递增,
所以当时,,
9.AC【详解】,,
由,可得,解之得
10.ABD【详解】对于A,根据回归直线经过样本点中心可得,得,故A正确;
对于B,根据独立性检验思想,的值越大,说明推断两事件无关出错的概率越大,因此两事件相关程度越大,故B正确;
对于C,回归分析是研究两个变量的相关关系,而独立性检验是对两个变量之间的是否具有某种关系的一种检验,故C不正确;
对于D,在残差的散点图中,残差分布的水平带状区域的宽度越窄,其模型的拟合效果越好,故D正确.
11.AD【详解】令,则,即,故A正确;
令,则,
即,
所以,故B错误;
根据二项式展开式的通项公式:,故C错误;
令,则,
令,则,
两式相加可得,①
两式相减可得,②
可得,
所以,故D正确.
12.【详解】对于A:因为,当A与B相互独立时,
此时,由于无法确定,的大小关系,
故无法确定与的大小关系,故A错误;
对于B:因为,则,
所以,即,所以A与B独立,故B正确;
对于C:若A与B独立,则,
又,所以,则,即,故C正确;
对于:因为A与B独立,且,,
所以,则,
所以,故D错误;
13.
【详解】由题得函数的定义域为,
因为函数是奇函数,所以,.
所以,所以.
14.64
【详解】(1)当从8门课中选修2门,则不同的选课方案共有种;
(2)当从8门课中选修3门,
(1)若体育类选修课1门,则不同的选课方案共有种;
(2)若体育类选修课2门,则不同的选课方案共有种;
综上所述:不同的选课方案共有种.
15.
【详解】解:由已知可得这家餐馆的好评率为.
16.
【详解】由题意,函数,则,
令,即,解得,
当时,的单调增区间为,,单调减区间为,
又由,,
可得在一个周期内,函数最大值为,即函数的最大值为.
17.【详解】(1)因为,且,所以,解得,
所以函数的解析式为.
(2)由(1)可知,;又,
所以曲线在处的切线方程为,即.
18.【详解】(1)的可能值为,,100,300,
,,
,,
所以的概率分布为
100 300
0.008 0.096 0.384 0.512
根据的概率分布,可得的期望
.
(2)这名同学总得分不为负分的概率为.
19.【详解】(1)依题意,X的可能取值为0,1,2,
则,,,
所以的分布列为:
0 1 2
故
(2)(i)依题意,可知这40只小白鼠体重增量的中位数是将两组数据合在一起,从小到大排后第20位与第21位数据的平均数,观察数据可得第20位为23.2,第21位数据为23.6,所以,
故列联表为:
合计
对照组 6 14 20
实验组 14 6 20
合计 20 20 40
(ii)零假设:小白鼠在高浓度臭氧环境中与正常环境中体重的增加量没有差异
由(i)可得,,
依据小概率值的独立性检验,我们推断假设不成立,即认为小白鼠在高浓度臭氧环境中与正常环境中体重的增加量有差异.
20.【详解】(1).
(2)因为,,
所以,.
因为,
所以学生的体质测试成绩恰好落在区间得概率约为0.9545,
故,所以.
21.【详解】(1)函数的定义域为,
.
若,则当时,,故在上单调递减;
若,则当时,当时,
故在上单调递减,在上单调递增.
(2)由(1)知,当时,在处取得最小值,
所以等价于,即.
设,则.
当时,,当时,,
所以在上单调递减,在上单调递增,
故当时,取得极小值且为最小值,最小值为.
所以当时,.
从而当时,,即.
22.【详解】(1)根据散点图判断,看出样本点分布在一条指数函数的周围,
所以适宜作为与间的回归方程模型;
令,则,,
,,
关于的回归方程为.
(2)由题意,设随机挑选一批,取出两个鱼卵,其中“死卵”个数为,则的取值为0,1,2,
设“所取两个鱼卵来自第批”,所以,
设“所取两个鱼卵有个”“死卵”,
由全概率公式
,
,
所以取出“死卵”个数的分布列为:
0 1 2
.
所以取出“死卵”个数的数学期望.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.集合,,则( )
A. B. C. D.
2.复数的虚部为( )
A. B. C.2 D.
3.展开式中含项的系数为( )
A.15 B.30 C.60 D.120
4.甲、乙两校各有3名教师报名支教,其中甲校2男1女,乙校1男2女,若从甲校和乙校报名的教师中各任选1名,则选出的2名教师性别相同的概率是( )
A. B. C. D.
5.曲线在点处的切线的倾斜角为( )
A. B. C. D.
6.小华为了研究数学名次和物理名次的相关关系,记录了本班五名同学的数学和物理的名次,如图,后来发现第四名同学的数据记录有误,那么去掉数据后,下列说法错误的是( )
A.样本相关系数变大 B.残差平方和变大
C.变大 D.解释变量与响应变量的相关程度变强
7.若函数在处有极值10,则( )
A. B. C.6 D.15
8.已知函数,,分别与直线交于点A,B,则的最小值为( )
A. B. C. D.
二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9.设向量,,若,则的取值可能是( )
A. B.0 C.3 D.5
10.下列关于回归分析与独立性检验的说法正确的是( )
A.相关变量x,y的线性回归方程为,若样本点中心为,则
B.对于独立性检验,的值越大,说明两事件相关程度越大
C.回归分析是对两个变量确定性关系的分析,而独立性检验是分析两个变量之间的不确定性关系
D.在残差的散点图中,残差分布的水平带状区域的宽度越窄,其模型的拟合效果越好
11.关,则( )
A.
B.
C.
D.
12.已知A,B是两个事件,且,,则下列结论一定成立的是( ).
A.
B.若,则与独立
C.若与独立,且,则
D.若与独立,且,,则
三、填空题:本题共4小题,每小题5分,共20分.
13.若为奇函数,则______.
14.某学校开设了4门体育类选修课和4门艺术类选修课,学生需从这8门课中选修2门或3门课,并且每类选修课至少选修1门,则不同的选课方案共有______种(用数字作答).
15.某餐馆在A网站有200条评价,好评率为90%,在B网站有100条评价,好评率为87%.综合考虑这两个网站的信息,这家餐馆的好评率为______.
16.已知函数,则的最大值为______.
四、解答题:本题共6小题,共70分.解答应写出文字说明 证明过程或演算步骤.
17.已知函数,且.
(1)求的解析式;
(2)求曲线在处的切线方程.
18.某同学参加科普知识竞赛,需回答三个问题.竞赛规则规定:每题回答正确得100分,回答不正确得—100.假设这名同学每题回答正确的概率均为0.8,且各题回答正确与否相互之间没有影响.
(1)求这名同学回答这三个问题的总得分的概率分布和数学期望;
(2)求这名同学总得分不为负分(即)的概率.
19.一项试验旨在研究臭氧效应.实验方案如下:选40只小白鼠,随机地将其中20只分配到实验组,另外20只分配到对照组,实验组的小白鼠饲养在高浓度臭氧环境,对照组的小白鼠饲养在正常环境,一段时间后统计每只小白鼠体重的增加量(单位:g).实验结果如下:对照组的小白鼠体重的增加量从小到大排序为:
15.2 18.8 20.2 21.3 22.5 23.2 25.8 26.5 27.5 30.1
32.6 34.3 34.8 35.6 35.6 35.8 36.2 37.3 40.5 43.2
实验组的小白鼠体重的增加量从小到大排序为:
7.8 9.2 11.4 12.4 13.2 15.5 16.5 18.0 18.8 19.2
19.8 20.2 21.6 22.8 23.6 23.9 25.1 28.2 32.3 36.5
(1)设X表示指定的两只小白鼠中分配到对照组的只数,求X的分布列和数学期望;
(2)(i)求40只小鼠体重的增加量的中位数m,再分别统计两样本中小于m与不小于的数据的个数,完成如下列联表:
对照组
实验组
(ii)根据(i)中的列联表,依据小概率值的独立性检验,能否认为小白鼠在高浓度臭氧环境中与正常环境中体重的增加量有差异.
附:,其中.
0.100 0.050 0.010
2.706 3.841 6.635
20.为了切实加强学校体育工作,促进学生积极参加体育锻炼,养成良好的锻炼习惯,某高中学校计划优化课程,增加学生体育锻炼时间,提高体质健康水平,某体质监测中心抽取了该校10名学生进行体质测试,得到如下表格:
序号i 1 2 3 4 5 6 7 8 9 10
成绩(分) 38 41 44 51 54 56 58 64 74 80
记这10名学生体质测试成绩的平均分与方差分别为,,经计算,.
(1)求;
(2)经统计,高中生体质测试成绩近似服从正态分布,用,的值分别作为,的近似值,若监测中心计划从全市抽查100名高中生进行体质测试,记这100名高中生的体质测试成绩恰好落在区间的人数为,求的数学期望.
附:若,则,,.
21.已知函数,.
(1)讨论的单调性;
(2)当时,证明.
22.经观测,长江中某鱼类的产卵数与温度有关,现将收集到的温度和产卵数的10组观测数据作了初步处理,得到如图的散点图及一些统计量表.
360 54.5 1360 44 384
3 588 32 6430
表中,,
(1)根据散点图判断,,与哪一个适宜作为与之间的回归方程模型并求出关于回归方程;(给出判断即可,不必说明理由)
(2)某兴趣小组抽取两批鱼卵,已知第一批中共有6个鱼卵,其中“死卵”有2个;第二批中共有8个鱼卵,其中“死卵”有3个.现随机挑选一批,然后从该批次中随机取出2个鱼卵,求取出“死卵”个数的分布列及数学期望.
附:对于一组数据,,,,其回归直线的斜率和截距的最小二乘估计分别为,.
数学科试卷
参考答案
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 A D C B A B D B AC ABD AD BC
13. 14.64 15. 16.
答案详解:
1.A【详解】解:因为,,所以.
2.D【详解】,故的虚部为.
3.C【详解】二项式的二项展开式的通项公式为,则展开式中含项的系数为.
4.B【详解】
5.A【详解】由和切点可知,切线的斜率,即倾斜角,
6.B【详解】由散点图知,去掉后,与的线性相关程度变强,且为正相关,所以变大,变大,残差平方和变小.故ACD正确,B错误.
7.D【详解】由,得,由题意可知:,,得到,解得或,当,时,,所以不是极值点,当,时,,
所以在,上单调递增,在上单调递减,所以则在处取极小值10,符合题意.
所以,,所以.
8.B【详解】
由题意,,,其中,且,
所以,令,,
则时,解得,
所以时,;时,;
则在上单调递减,在上单调递增,
所以当时,,
9.AC【详解】,,
由,可得,解之得
10.ABD【详解】对于A,根据回归直线经过样本点中心可得,得,故A正确;
对于B,根据独立性检验思想,的值越大,说明推断两事件无关出错的概率越大,因此两事件相关程度越大,故B正确;
对于C,回归分析是研究两个变量的相关关系,而独立性检验是对两个变量之间的是否具有某种关系的一种检验,故C不正确;
对于D,在残差的散点图中,残差分布的水平带状区域的宽度越窄,其模型的拟合效果越好,故D正确.
11.AD【详解】令,则,即,故A正确;
令,则,
即,
所以,故B错误;
根据二项式展开式的通项公式:,故C错误;
令,则,
令,则,
两式相加可得,①
两式相减可得,②
可得,
所以,故D正确.
12.【详解】对于A:因为,当A与B相互独立时,
此时,由于无法确定,的大小关系,
故无法确定与的大小关系,故A错误;
对于B:因为,则,
所以,即,所以A与B独立,故B正确;
对于C:若A与B独立,则,
又,所以,则,即,故C正确;
对于:因为A与B独立,且,,
所以,则,
所以,故D错误;
13.
【详解】由题得函数的定义域为,
因为函数是奇函数,所以,.
所以,所以.
14.64
【详解】(1)当从8门课中选修2门,则不同的选课方案共有种;
(2)当从8门课中选修3门,
(1)若体育类选修课1门,则不同的选课方案共有种;
(2)若体育类选修课2门,则不同的选课方案共有种;
综上所述:不同的选课方案共有种.
15.
【详解】解:由已知可得这家餐馆的好评率为.
16.
【详解】由题意,函数,则,
令,即,解得,
当时,的单调增区间为,,单调减区间为,
又由,,
可得在一个周期内,函数最大值为,即函数的最大值为.
17.【详解】(1)因为,且,所以,解得,
所以函数的解析式为.
(2)由(1)可知,;又,
所以曲线在处的切线方程为,即.
18.【详解】(1)的可能值为,,100,300,
,,
,,
所以的概率分布为
100 300
0.008 0.096 0.384 0.512
根据的概率分布,可得的期望
.
(2)这名同学总得分不为负分的概率为.
19.【详解】(1)依题意,X的可能取值为0,1,2,
则,,,
所以的分布列为:
0 1 2
故
(2)(i)依题意,可知这40只小白鼠体重增量的中位数是将两组数据合在一起,从小到大排后第20位与第21位数据的平均数,观察数据可得第20位为23.2,第21位数据为23.6,所以,
故列联表为:
合计
对照组 6 14 20
实验组 14 6 20
合计 20 20 40
(ii)零假设:小白鼠在高浓度臭氧环境中与正常环境中体重的增加量没有差异
由(i)可得,,
依据小概率值的独立性检验,我们推断假设不成立,即认为小白鼠在高浓度臭氧环境中与正常环境中体重的增加量有差异.
20.【详解】(1).
(2)因为,,
所以,.
因为,
所以学生的体质测试成绩恰好落在区间得概率约为0.9545,
故,所以.
21.【详解】(1)函数的定义域为,
.
若,则当时,,故在上单调递减;
若,则当时,当时,
故在上单调递减,在上单调递增.
(2)由(1)知,当时,在处取得最小值,
所以等价于,即.
设,则.
当时,,当时,,
所以在上单调递减,在上单调递增,
故当时,取得极小值且为最小值,最小值为.
所以当时,.
从而当时,,即.
22.【详解】(1)根据散点图判断,看出样本点分布在一条指数函数的周围,
所以适宜作为与间的回归方程模型;
令,则,,
,,
关于的回归方程为.
(2)由题意,设随机挑选一批,取出两个鱼卵,其中“死卵”个数为,则的取值为0,1,2,
设“所取两个鱼卵来自第批”,所以,
设“所取两个鱼卵有个”“死卵”,
由全概率公式
,
,
所以取出“死卵”个数的分布列为:
0 1 2
.
所以取出“死卵”个数的数学期望.
同课章节目录
